机械式自动变速器(Automatic Mechanical Transmission,AMT)具有传动效率高、燃油经济性好、生产继承性良好等优点,是符合中国国情的自动变速器,其关键部件离合器的控制规则是AMT系统的重点和难点[1]。大多文献关于AMT起步控制的研究主要集中在离合器接合速度和位移方面[2-3],而没有考虑离合器摩擦因数随温度的变化带来的影响。
在离合器结合过程中,摩擦片在飞轮、压盘之间滑磨,产生热量,由此使摩擦片表面温度升高[4];另一方面,车辆主要在城市循环工况行驶,在交通拥堵时经常重复起步,短时间内无法充分散热,这必然导致汽车离合器温度极高。温度改变,则摩擦系数改变,离合器传递的转矩也随之变化。
笔者根据离合器摩擦副表面温度和摩擦因数的变化关系,通过离合器转矩传递模型,分析了摩擦因数对汽车起步的影响,为AMT正常安全起步提供参考。
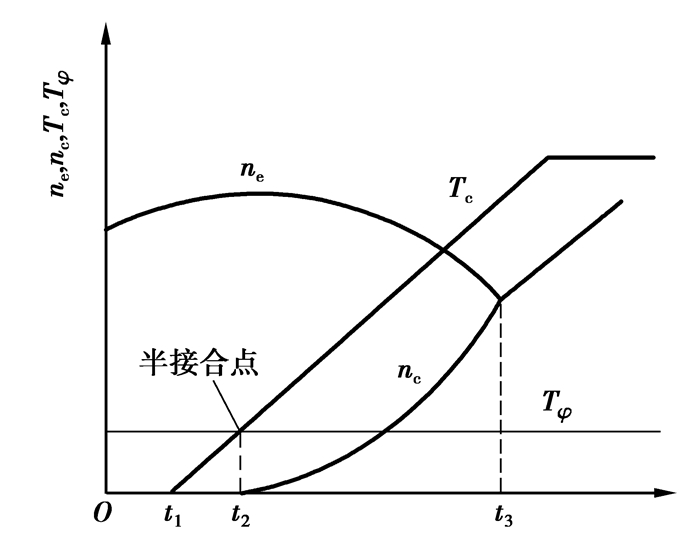
1 汽车起步过程的分析车辆起步时,主从动盘逐渐接合,间隙逐渐减小,当间隙为零时,从动盘在摩擦力的作用下,转速从零逐渐增大(此时车辆也从静止运行起来),转速差逐渐减小,直到从动盘转速与主动盘转速相同时,起步完成[5]。起步过程离合器的接合可以分为4个部分,如图 1所示[6-7]。
|
图 1 离合器起动 |
1) 0~t1为空行程阶段,此时主从动盘正逐渐接合但未接触,所以没有产生摩擦力矩。
2) t1~t2为克服阻力阶段,此阶段主、从动片开始滑磨,但传递到从动盘的转矩小于汽车的阻力矩,所以汽车还未运动。
3) t2~t3为滑磨阶段,此时传递到从动盘的转矩大于汽车的阻力矩,汽车开始运动,离合器主、从动盘还没有同步。
4) t3以后为同步阶段,此时离合器主、从动盘转速相同,消除了转速差,汽车起步成功。
2 汽车起步动力学模型的建立 2.1 发动机输出转矩模型发动机输出转矩与发动机节气门开度和发动机转速的关系为
| $ {T_{\rm{e}}} = f\left( {a, {n_{\rm{e}}}} \right), $ | (1) |
式中:Te为发动机输出转矩;a为节气门开度;ne为发动机转速。
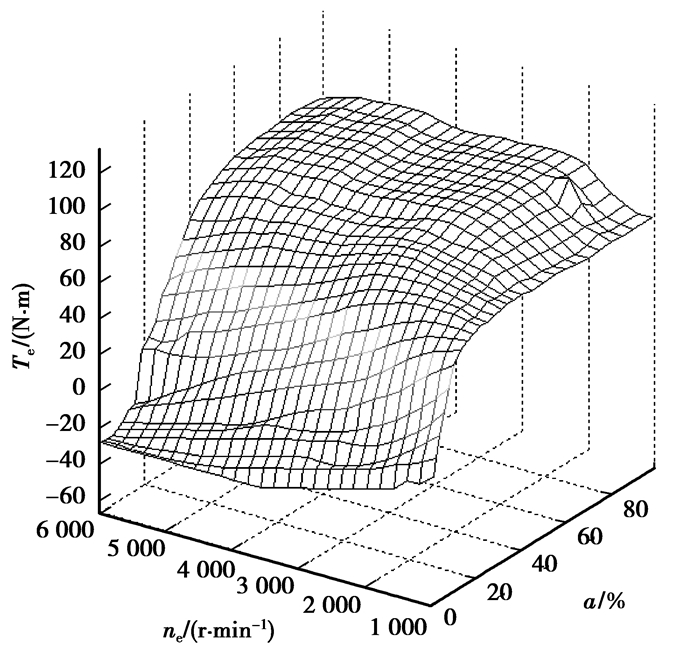
在节气门确定的条件下,通过实验数据3次样条插值,可以获得精确的发动机输出转矩曲线[8],因此发动机的数值模型可通过有限的试验数据建立。由式(1)可知,在发动机节气门开度和转速确定的条件下,发动机在稳态工况下的输出扭矩即可确定,如图 2所示。
|
图 2 扭矩图 |
发动机基本处于动态工况,所以不能用稳态的输出转矩代替,但发动机稳态工况下的输出扭矩可通过修正系数的方法进行修正,转换为动态转矩[9]。
| $ T{_{\rm{e}}^{\rm{D}} = }{T_{\rm{e}}} - \lambda \frac{{{\rm{d}}{\omega _{\rm{e}}}}}{{{\rm{d}}t}}, $ | (2) |
式中:TeD为发动机动态输出扭矩,N·m;Te为发动机稳态输出扭矩,N·m;λ为非稳态工况下发动机输出扭矩下降系数。文中λ值取0.15;dωe/dt为发动机曲轴角加速度,1/s2。
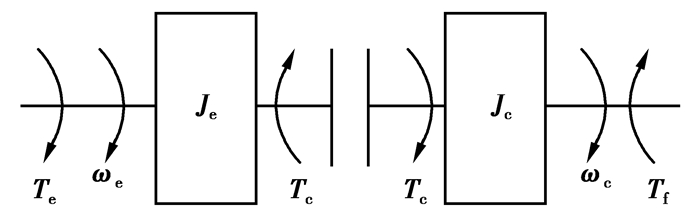
2.2 离合器动力学模型为了简化模型和快速建模,将发动机和传动轴系的当量转动惯量分别计算到离合器的主、从动盘上[10],简化后的模型如图 3所示。
|
图 3 离合器简化力学模型 |
由动力学原理,在汽车起步过程中离合器的动力学模型为
1) 0~t1过程无转矩。
2) t1~t2过程离合器主从动盘有接触,但传递的转矩过小,所以从动盘转速为零。
| $ \left\{ \begin{array}{l} {J_{\rm{e}}}{\rm{d}}{\omega _{\rm{e}}}{\rm{/d}}t = {T_{\rm{e}}}-{T_{\rm{c}}}, \\ {\omega _{\rm{c}}} = 0。\end{array} \right. $ | (3) |
3) t2~t3过程汽车刚刚运动,离合器主、从动盘还存在滑磨,而离合器从动盘转矩和转速不断增加。
| $ \left\{ \begin{array}{l} {J_{\rm{e}}}{\rm{d}}{\omega _{\rm{e}}}{\rm{/d}}t = {T_{\rm{F}}}-{T_{\rm{F}}}, \\ {J_{\rm{c}}}{\rm{d}}{\omega _{\rm{c}}}{\rm{/d}}t = {T_{\rm{c}}}-{T_{\rm{f}}}。\end{array} \right. $ | (4) |
4) t3以后离合器主、从动盘达到同步。
| $ \left( {{J_{\rm{e}}}{\rm{ + }}{J_{\rm{c}}}} \right){\rm{d}}{\omega _{\rm{e}}}/{\rm{d}}t = {T_{\rm{e}}}-{T_{\rm{f}}}。$ | (5) |
式中:Tc为离合器从动盘传递的转矩;Tf为外界阻力矩转换到变速器输入轴上的当量阻力矩;Je为发动机旋转部分和离合器主动盘的转动惯量;Jc为离合器从动盘带动的所有转动部件和整车转换到离合器从动盘上的当量转动惯量;ωe为发动机角速度;ωc为离合器从动盘角速度。
2.3 起步时从动盘阻力矩的确定在起步阶段,车速很小,所以不计风阻。离合器从动盘的当量阻力矩主要是滚动阻力和坡度阻力经动力传动系转化的[11]。
| $ {T_{\rm{f}}}{i_{\rm{g}}}{i_{\rm{o}}}{\eta _{\rm{m}}} = {M_{\rm{a}}}g\left( {f\;\cos \;\alpha + \sin \;\alpha } \right){R_{\rm{r}}}, $ | (6) |
整理得
| $ {T_{\rm{f}}} = \frac{{{M_{\rm{a}}}g{R_{\rm{r}}}}}{{{i_{\rm{g}}}{i_{\rm{o}}}{\eta _{\rm{m}}}}}\left( {f\;\cos \;\alpha + \sin \;\alpha } \right), $ | (7) |
式中:α为道路坡度角;f为轮胎滚动阻力系数;ηm为传动系传动效率。
2.4 离合器转矩传递模型结合时,离合器主从动片产生摩擦,离合器正是利用摩擦来传递转矩,其模型[12]为
| $ {T_{\rm{c}}} = {\rm{sign}}\left( {{\omega _{\rm{e}}}-{\omega _{\rm{c}}}} \right)\mu \left( {{T_{\rm{s}}}} \right)F\left( t \right)Z \times \frac{2}{3}\left( {\frac{{R_0^3-R_1^3}}{{R_0^2-R_1^2}}} \right), $ | (8) |
其中
| $ \begin{array}{l} {\rm{sign}}\left( {{\omega _{\rm{e}}}-{\omega _{\rm{c}}}} \right) = {\rm{sign}}\;\Delta \omega = \\ \;\;\;\;\;\;\;\left\{ \begin{array}{l} 1, {\omega _{\rm{e}}}-{\omega _{\rm{c}}} \ge 0, \\ -1, {\omega _{\rm{e}}} - {\omega _{\rm{c}}} < 0。\end{array} \right. \end{array} $ | (9) |
式中:μ(Ts)为干式离合器的动摩擦因数;Ts为压盘表面温度;Δω为主、从动盘角速度差;F(t)为压盘所受到的压紧力;Z为摩擦副数;R0为摩擦片外径;R1为摩擦片内径。
由式(8)可知,离合器传递的转矩受摩擦因数和压盘压紧力的影响,而离合器片摩擦因数主要受压盘表面温度(滑摩功)的影响。汽车正常起步的关键在于离合器传递转矩的控制,所以压盘表面温度是汽车起步的重要因素。
2.5 摩擦表面温度计算模型离合器滑磨时产生滑摩功,它表明摩擦力的大小,其表达式[13]为
| $ {L_{\rm{c}}}{\rm{ = }}\int_0^{{t_1}} {{T_{\rm{c}}}\left( t \right)} {\omega _{\rm{e}}}{\rm{d}}t + \int_{{t_1}}^{{t_2}} {{T_{\rm{c}}}\left( t \right)} \left( {{\omega _{\rm{e}}}-{\omega _{\rm{c}}}} \right){\rm{d}}t, $ | (10) |
式中:Tc(t)为离合器从动盘所传递的转矩;t1为离合器从动盘所传递的转矩等于汽车所受阻力矩的时刻;t2为离合器主、从动盘转速相等的时刻。
在起步过程中,离合器产生的热量主要被发动机飞轮和离合器压盘吸收,而离合器的散热主要在起步完成之后,所以摩擦片平均温升[14]为
| $ {T_{\rm{a}}} = rQ/\left( {m{c_{\rm{p}}}} \right), $ | (11) |
式中:Q为滑磨过程产生的总热量,即Q=ncLc;Ta为摩擦片的平均温度;r为传到压盘的热量所占的比率;m为压盘的质量;cp为压盘的比热容;nc为吸热效率;Lc为离合器在起步过程中的滑磨功。
通过研究,在起步刚刚完成时,离合器压盘的表面温度远远大于平均温度,它们的关系为
| $ {T_{\rm{s}}} = \left( {\frac{{0.35}}{{\varphi + 0.04}} + 0.95} \right){T_{\rm{a}}} + {T_0}, $ | (12) |
其中无量纲系数
| $ \varphi = \psi {t_{\rm{c}}}{\rm{/}}{\left( {h/2} \right)^2}。$ | (13) |
式中:T0为离合器摩擦面的初始温度;ψ为压盘的热扩散率;tc为离合器滑磨时间;h为压盘的厚度。
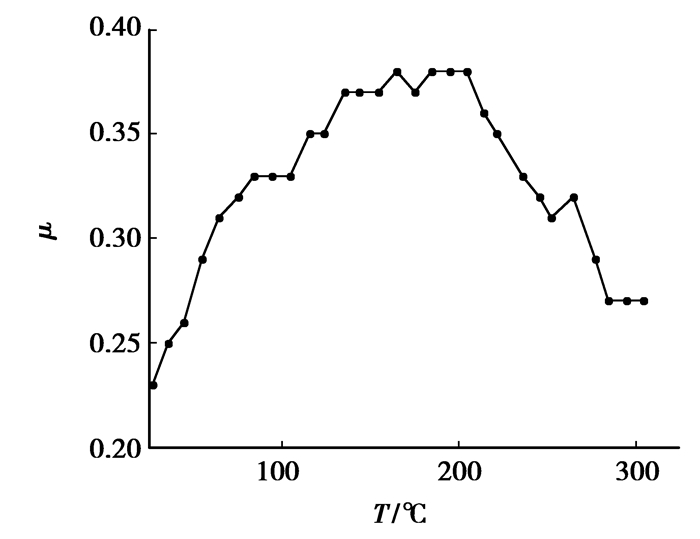
2.6 摩擦因数与转矩的确定以多数国内微车制造商选用的离合器摩擦面片为研究对象,通过试验[15],得出了上述摩擦片的摩擦因数随摩擦面温度的变化关系,如图 4所示。由图 4可知,曲线趋势是先增加后减少,当温度为165 ℃左右时摩擦系数取得最大值;高于165 ℃后,摩擦系数下降非常快。
|
图 4 摩擦因数随摩擦面温度的变化 |
根据传动系统动力学模型,采用“快慢快”的方式控制离合器的结合速度,依据某原型车性能参数,利用Matlab/Simulink软件建立起步工况离合器滑磨功仿真计算模型,对滑摩功进行仿真计算。一次起步的分离接合过程如图 5所示,仿真计算得到离合器的滑摩功曲线如图 6所示。
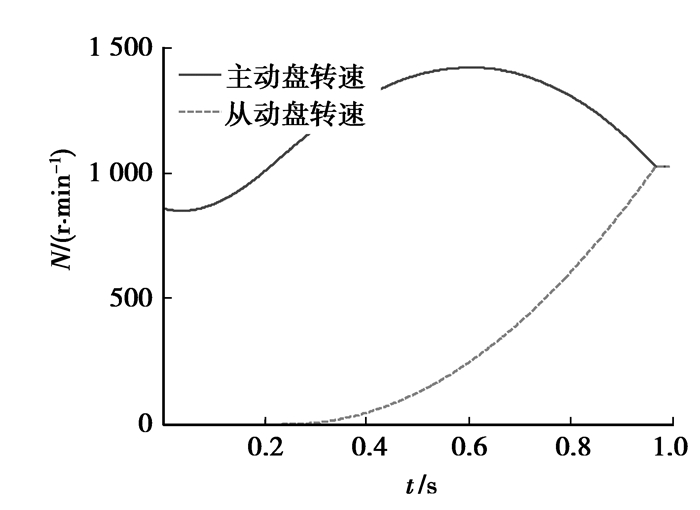
|
图 5 一次起步离合器结合过程 |
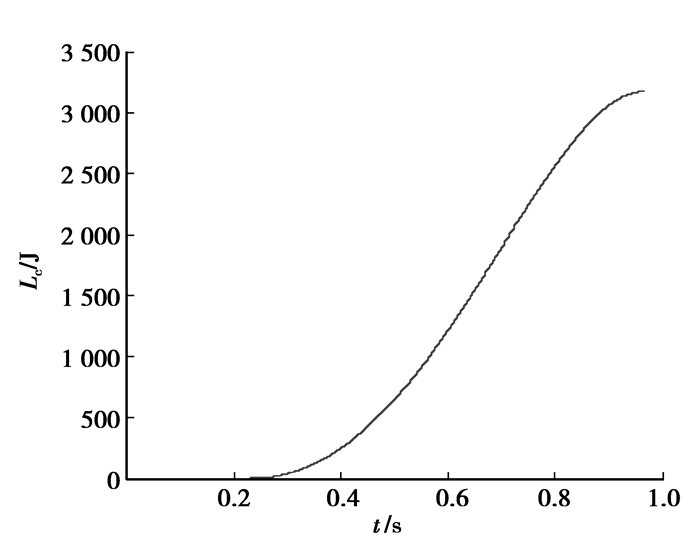
|
图 6 一次结合的滑摩功 |
为了降低模型的复杂程度和加快建模,连续起步模型做了如下假设:1)连续起步时间较短,在建模时忽略了离合器的散热能力。2)由于滑摩功的产生主要在离合器的滑磨阶段,当主、从动盘同步时,即图 1的t3时,就完成1次起步;主、动盘同步后,过0.5 s汽车进行第2次起步。3)每次起步的工况相同。按以上假设完成多次重复起步,离合器接合过程如图 7、8所示,压盘表面温度变化如图 9、10所示。
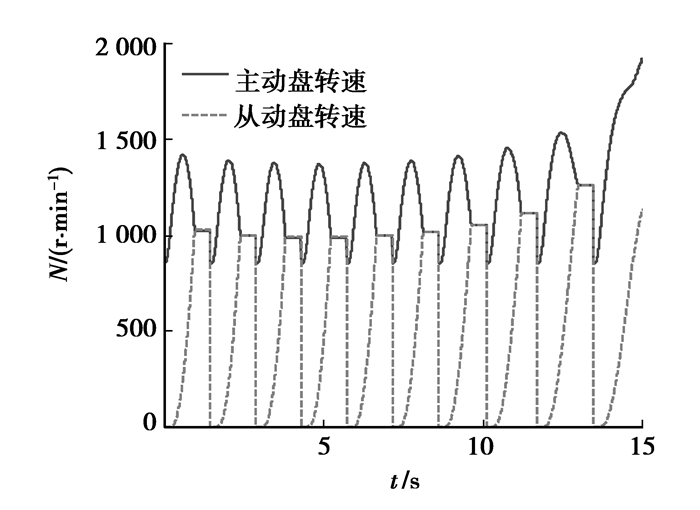
|
图 7 多次起步过程(摩擦系数为变量) |
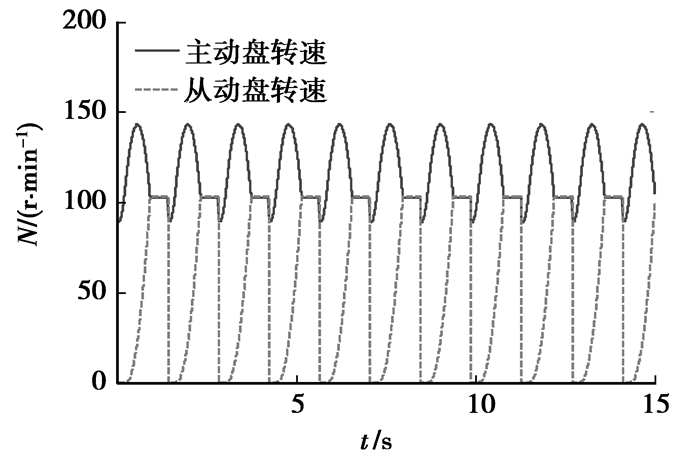
|
图 8 多次起步过程(摩擦系数为定值) |
|
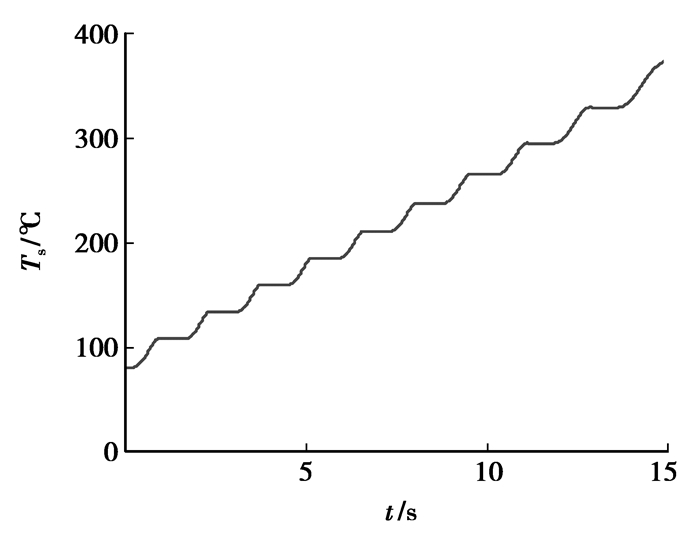
图 9 多次起步压盘表面温度变化(摩擦系数为变量) |
|
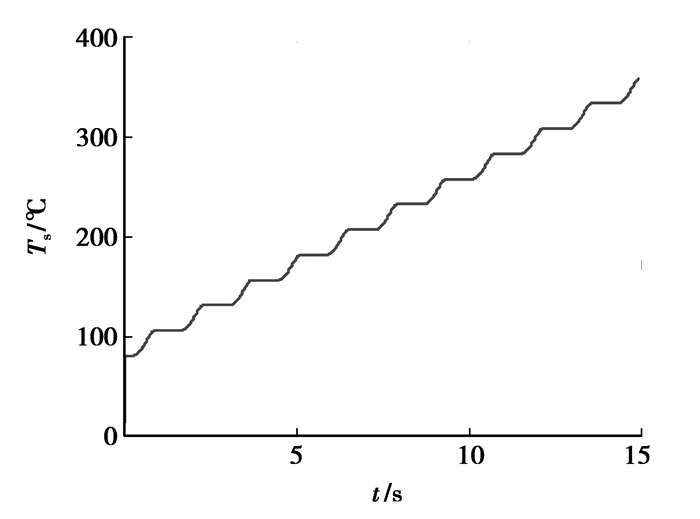
图 10 多次起步压盘表面温度变化(摩擦系数为定值) |
1) 由图 7可知,随着重复起步的次数增多,离合器主动盘最大转速先逐渐降低然后逐渐增高,起步时间也先逐渐缩短后逐渐增长。这和摩擦系数随温度变化的抛物线关系类似。而图 8中,每次离合器主动盘转速相同。图 9中,随着起步次数增加,单次离合器表面的温升先减少然后增加。而图 10中,每次起步温升相同。可见,摩擦系数的变化对主从动盘转速,起步时间和温度有相应的影响。
2) 由图 7,第10次起步中,由于摩擦系数变得很小,相应离合器传递的转矩也变得很小。最终导致主动盘转速和滑摩功猛增。离合器主、从动盘一直处于滑磨状态。摩擦片将会因烧蚀而永久损坏。
4 结论从以上仿真的结果和分析可知,在AMT的起步控制中,摩擦系数对起步的影响不可忽视:
1) 随着重复起步的次数增多,离合器主动盘最大转速先降低然后增高,起步时间先变短后变长。
2) 重复起步多次后,摩擦系数变得很小,相应离合器传递的转矩也变得很小,无法完成正常起步。
3) 在AMT起步中,应尽量减少连续起步次数,且每次起步间隔应尽可能长。在起步控制中,可以限定单位时间的起步次数。
4) 在起步过程中,为减小摩擦系数对离合器转矩的传递产生影响,离合器结合时可适当调节离合器的结合量。起步多次时可以牺牲冲击度来减小温升。
| [1] | Knut N, Hans H. Developments in automated clutch management systems[C]//Proceedings of the International Congress & Exposition, February 27, 1995, Detroit, Michigan, United States.[S.l.]:SAE Technical Paper, 1995:950896. http://dx.doi.org/10.4271/950896 |
| [2] | Xie X P, Wang X D, Zhang X, et al. Fuzzy control of clutch for automatic mechanical transmission vehicle starting[C]//Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, September 3-5, 2008, Harbin, China. Piscataway:IEEE Press, 2008:1-4. http://ieeexplore.ieee.org/document/4677445/ |
| [3] | Liu W G, He R. Fuzzy control of AMT clutch engagement during the vehicle starting[C]//Proceedings of the 9th International Conference of Chinese Transportation Professionals, ICCTP 2009:Critical Issues in Transportation System Planning, Development, and Management, August 5-9, 2009, Harbin, China. New York:ASME, 2009:1974-1982. https://www.researchgate.net/publication/269150987_Fuzzy_Control_of_AMT_Clutch_Engagement_during_the_Vehicle_Starting |
| [4] | 徐石安, 江发潮. 汽车离合器[M]. 北京: 清华大学出版社, 2005. |
| [5] |
刘振军, 秦大同, 叶明.
电控机械自动变速车辆发动机转速控制[J]. 重庆大学学报:自然科学版, 2007, 30(11): 5–8.
LIU Zhenjun, QIN Datong, YE Ming. Engine rotational speed control of an AMT vehicles[J]. Journal of Chongqing University:Natural Science Edition, 2007, 30(11): 5–8. (in Chinese) |
| [6] | Niu Q Y. Clutch control during starting of AMT[J]. Procedia Engineering, 2010, 7: 447–452. |
| [7] |
胡建军, 胡宏奎, 伍国强, 等.
重型商用车ATM自动控制策略及试验分析[J]. 重庆大学学报, 2010, 33(6): 31–41.
HU Jianjun, HU Hongkui, WU Guoqiang, et al. Automatic control strategy and its test analysis for the heavy truck AMT[J]. Journal of Chongqing University, 2010, 33(6): 31–41. DOI:10.11835/j.issn.1000-582X.2010.06.006 (in Chinese) |
| [8] | 余志生. 汽车理论[M]. 3版. 北京: 机械工业出版社, 2004. |
| [9] | 雷晓东. 电控机械自动变速系统换档控制策略研究[D]. 重庆: 重庆大学硕士学位论文, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10611-2005145589.htm |
| [10] | Kong G L, Zhong Z M, Yu Z P. A method of calibration of clutch torque transfer feature based on AMT launch control[J]. Procedia Engineering, 2011, 16: 88–94. DOI:10.1016/j.proeng.2011.08.1056 |
| [11] | Wang H, Zhou W, Qian D C, et al. Study on control strategy of starting process for clutch of AMT vehicle[C]//Proceedings of the 20112nd International Conference on Mechanic Automation and Control Engineering, July 15-17, 2011, Hohht, China. Piscataway:IEEE Press, 2011:5285-5288. http://ieeexplore.ieee.org/document/5988184/ |
| [12] |
胡建军, 李光辉, 伍国强, 等.
汽车起步过程离合器传递转矩精确计算分析[J]. 汽车工程, 2008, 30(12): 1083–1086.
HU Jianjun, LI Guanghui, WU Guoqiang, et al. Accurate calculation of clutch torque transmission during vehicle starting[J]. Automotive Engineering, 2008, 30(12): 1083–1086. DOI:10.3321/j.issn:1000-680X.2008.12.013 (in Chinese) |
| [13] | Wu S J, Zhu E Y, Ren H, et al. Study on control strategy of clutch engagement based on fuzzy control during vehicle starting[C]//Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, March 31-April 2, 2009, Los Angeles, California, United States. Piscataway:IEEE Press, 2009, 5:82-86. https://www.computer.org/csdl/proceedings/csie/2009/3507/05/3507e082-abs.html |
| [14] |
吕俊成.
微型汽车离合器摩擦片表面平均温度计算研究[J]. 机械工程师, 2012(3): 152–153.
Lü Juncheng. Study on calculation of average temperature for clutch friction pair on micro car[J]. Mechanical Engineer, 2012(3): 152–153. (in Chinese) |
| [15] |
吕俊成, 莫易敏, 汤春球.
摩擦面温度对微车离合器摩擦材料摩擦因数影响的研究[J]. 中国机械工程, 2009, 20(14): 1677–1680.
Lü Juncheng, MO Yimin, TANG Chunqiu. Research on influence of friction surface temperature on the friction coefficient of micro-car clutch friction material[J]. China Mechanical Engineering, 2009, 20(14): 1677–1680. DOI:10.3321/j.issn:1004-132X.2009.14.010 (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

