2. 重庆电子工程职业学院, 重庆 401331;
3. 重庆光大产业有限公司, 重庆 401120
2. Chongqing College of Electronic Engineering, Chongqing 401331, China;
3. Chongqing Guangda Industry Co., Ltd., Chongqing 401120, China
车辆行驶过程中,频繁的加速、减速及制动和发动机的输出转矩和转速(输入激励的频率)的不规则性,使得车辆动力传动系统这样一个多自由度弹性系统经常处于冲击和振动的动态过程,当输入激励的频率与驱动系统的固有频率接近或相等时,将产生强烈的共振,更加剧了传动系统的扭转振动。为解决车辆动力传动系统的扭转振动问题,德国LUK公司于1989年研制出双质量飞轮,经过10年的不断改进,投入批量生产,对降低车辆传动系统的扭转振动和噪声、缓解传动系的冲击、实现对发动机的过载保护和使得发动机能在非常低的转速下运行从而降低燃油消耗等方面都发挥了重要的作用[1-5]。目前世界上掌握双质量飞轮核心设计制造技术的仅有德国的LUK、Sachs、美国的GAT和加拿大的Magna等公司,几乎垄断了全球双质量飞轮产品大部分的市场。目前中国引进国外整车生产技术车辆所搭载的双质量飞轮全部系购买外资企业的产品或进口。
随着增压、直喷为代表的关键技术的突破,发动机的功率转矩不断提升,对双质量飞轮的转矩特性提出了更高的要求。若依靠单纯增加弹簧的刚度来实现大扭转角条件下的高转矩特性,则在小扭转角条件下,不能满足一阶固有频率对应的转速低于发动机怠速转速。为解决该难点,德国LUK公司等研究出各段刚度为常数的分段变刚度的双质量飞轮,实现了小扭转角时的柔性和高转速时高反抗转矩的大刚度[6]。文献[7]对这种分段变刚度的双质量飞轮进行了研究,指出了由刚度切换所带来的阶跃,从而导致产生冲击载荷和噪声。为探索新型的减振装置,Sachs公司应用拓扑学的理论,提出了用方法树对影响双质量飞轮减振性能的各参数进行研究分析[8]。文献[9]对双质量飞轮的初级飞轮的内壁提出了曲线修正而产生形状约束并经试验验证,实现了连续变刚度的高转矩特性。文献[10-11]对双质量飞轮产品的减振原理特性进行了分析及试验方法研究。文献[12]对车辆可变阻尼器进行了动力学与数学建模,描述了阻尼随行程变化的特性。文献[13-14]分别对角位移、扭转刚度和扭转阻尼系数随振动频率以及减振器阻尼的变化情况进行了有意义的试验研究。文献[15]对周向短弹簧双质量飞轮的转矩转角特性进行了研究,但没有考虑摩擦因素对转矩特性的影响。文献[16]虽研究了摩擦特性对双质量转矩特性的影响,但没有解决弹簧座楔入后由摩擦特性所产生高反抗转矩的问题。笔者通过建立完整的基于摩擦特性的双质量飞轮转矩数学力学模型,利用弹簧座头部的形状约束,在大扭转角时由弹簧座相互楔入增加摩擦从而进一步增大了反抗转矩,实现了所希望的设计目标。
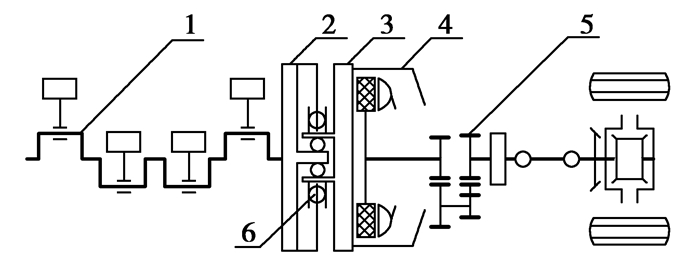
1 双质量飞轮的结构汽车动力传动系统如图 1所示,发动机曲轴1与初级飞轮2固联,由减振器6带动次级飞轮3,经离合器4将运动和动力输入到变速箱5。
|
图 1 汽车动力传动系统 1.发动机;2.初级飞轮;3.次级飞轮;4.离合器;5.变速箱;6.减振器 |
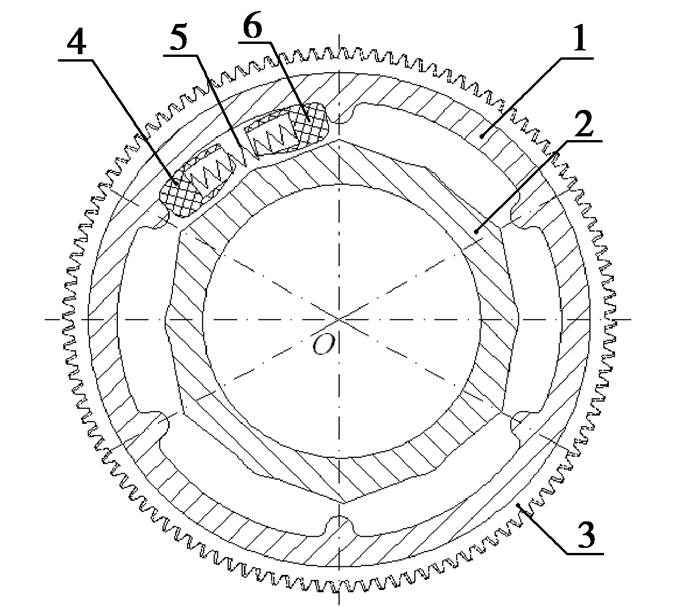
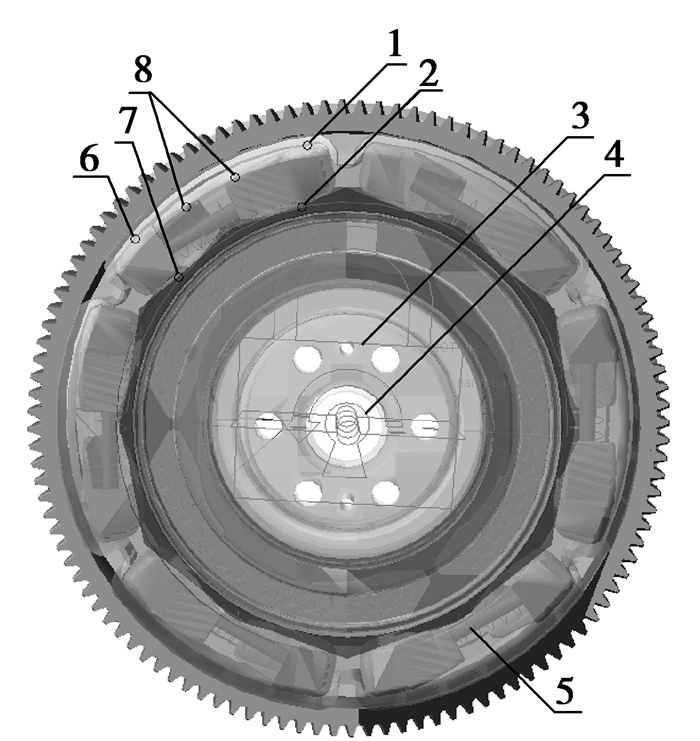
所研究的双质量飞轮实物结构如图 2所示,结构示意如图 3所示。减振器由弹簧座4、6和弹簧5组成。安装在初级飞轮的两个凸缘之间。工作过程中,随着扭转角的增大,分别与初级飞轮的内圆壁面、次级飞轮的多边形外缘面接触。弹簧座的楔入面为一多段圆弧面组合,该曲面形状保证了两弹簧座的顺利楔入和有效的侧向定位。弹簧座头部及根部的形状也保证了弹簧被压缩至极限位置时对弹簧的过载保护。
|
图 3 双质量飞轮结构示意 |

|
图 2 双质量飞轮实物 1.初级飞轮;2.次级飞轮;3.启动齿圈;4、6.弹簧座;5.弹簧 |
工作过程分为2个阶段,第1阶段为次级飞轮与弹簧座6接触而压缩弹簧5产生反抗转矩。第2阶段弹簧座头部开始楔入,由于摩擦增大而增加了反抗转矩。
2.1 楔入接触前的转矩特性双质量飞轮的结构参数坐标系如图 4所示。
|
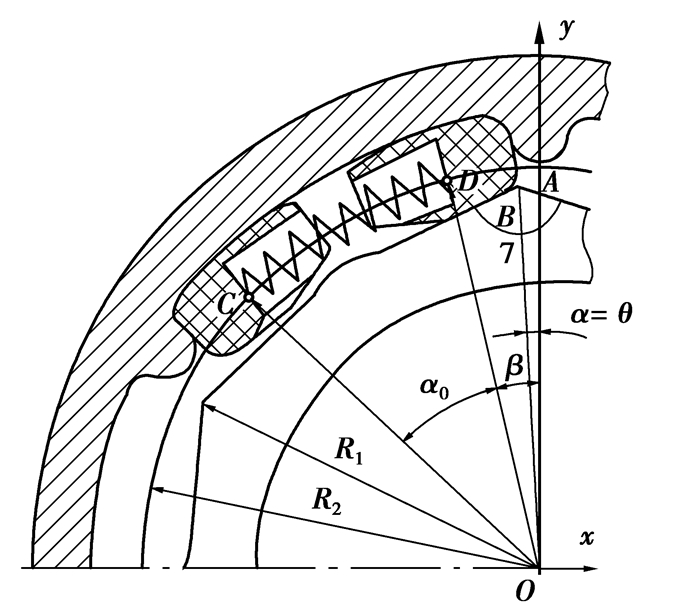
图 4 结构参数坐标系 |
图中,R1为次级飞轮最大向径,R2为弹簧分布半径,γ为次级飞轮的多边形顶角,θ为双质量飞轮空转角,β为双质量飞轮转动过空转角时弹簧端点D与回转中心O的连线OD与垂直方向的夹角,α为双质量飞轮转角(图中α=θ)。B点为弹簧座与次级飞轮的接触点,A点为次级飞轮多边形的顶点,LAB=b。C、D分别为弹簧座对弹簧的两支撑点,周向短弹簧其工作过程可近似为一直弹簧,其初始长度为L0=2R2sin (α0/2),α0为对应的初始张角。
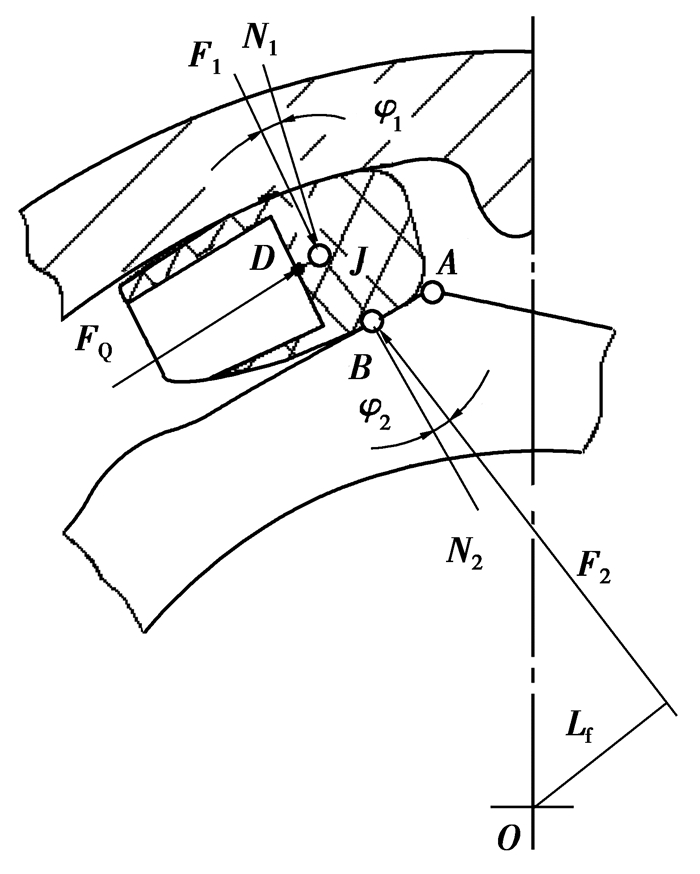
如图 5所示,弹簧座与次级飞轮在B点接触,FQ为弹簧力,设初级飞轮、次级飞轮与弹簧座的摩擦系数分别为μ1、μ2,相应的摩擦角为φ1=cotμ1、φ2=cotμ2。N1、N2为正压力,F1、F2分别为考虑摩擦后初级飞轮和次级飞轮对弹簧座的总反力。
|
图 5 弹簧座受力分析 |
转过扭转角α时弹簧长度为
| $ {L_{CD}} = 2{R_2}\sin \frac{{{\alpha _0}-\left( {\alpha-\theta } \right)}}{2}。$ | (1) |
设kt为弹簧线刚度,弹簧力
| $ \begin{array}{l} {F_Q}{\rm{ = }}{k_t}\left( {{L_0}-L} \right) = \\ \;\;\;\;\;\;4{R_2}{k_t}\sin \frac{{\alpha-\theta }}{4}\cos \frac{{2{\alpha _0}-\alpha + \theta }}{4}。\end{array} $ | (2) |
FQ的作用线斜率方程为
| $ {k_{CD}} = \frac{{{y_D}-{y_C}}}{{{x_D}-{x_C}}}, $ | (3) |
式中:xC、yC、xD、yD分别为C、D点的横坐标和纵坐标。
次级飞轮对弹簧座的正压力N2的作用线斜率为
| $ {k_{{N_2}}} = \tan \left( {\alpha-\frac{\gamma }{2}} \right)。$ | (4) |
总反力F2的作用线斜率为
| $ {k_{{F_2}}} = \tan \left( {\alpha-\frac{\gamma }{3} + {\varphi _2}} \right)。$ | (5) |
作用于弹簧座的FQ、F1、F2平衡,由所构成的首尾相接的力封闭三角形,得出F2与FQ的关系为
| $ {F_2} = \frac{{{F_{\rm{Q}}}\sin \;{\psi _1}}}{{\sin \;{\varphi _2}}}, $ | (6) |
式中:ψ1、ψ2分别为FQ与F1及F1与F2的夹角,坐标xB、yB均可由图 4及图 5的几何关系求得。
双质量飞轮传递的转矩
| $ {T_1} = m{F_2}{L_f} + {T_f}, $ | (7) |
式中:Lf为F2对回转中心O的力臂,
弹簧座头部开始楔入,由于弹簧座在接触过程中存在弹性变形,故引入接触变形模型,将弹簧座头部楔入接触假设为一种非线性的弹簧阻尼系统模型,用冲击函数法,其中接触力N包括弹性力和阻尼力,接触力表达式为
| $ N = K{\delta ^e} + D\left( {{\rm{d}}\;\delta /{\rm{d}}\;t} \right), $ | (8) |
式中:K为两个实体接触的刚度系数;δ为接触过程中的弹性变形量;e为接触指数;阻尼因子
| $ D = C\max {\left( {\frac{\delta }{d}} \right)^2}\left( {3-2 \times \frac{\delta }{d}} \right)。$ | (9) |
阻尼因子函数曲线如图 6所示,表示两个实体一开始接触变形量为0时,阻尼因子为0,随着变形量δ开始增大,阻尼因子也逐渐增加,当变形量达到最大值d时,阻尼因子达到最大值Cmax。
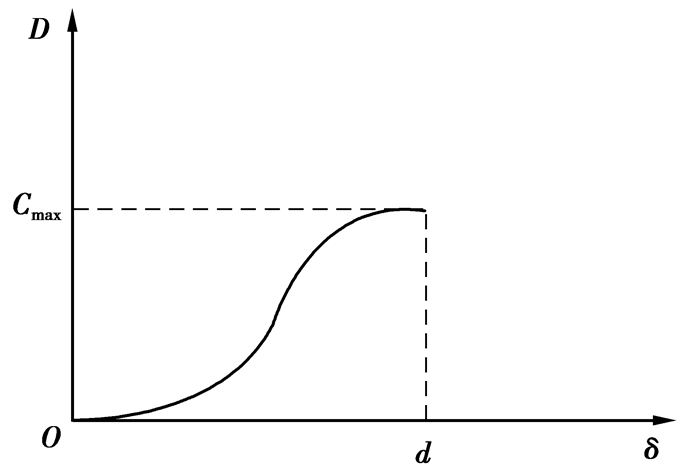
|
图 6 阻尼系数特性曲线 |
图 7为弹簧座4、6头部楔入接触后的受力分析图。其中N3为两弹簧座接触表面产生的接触力,δ为弹簧座接触后的弹性变形量,Fμ表示接触表面产生的摩擦力,Fμ=μ3·N3,μ3为弹簧座之间的摩擦系数,根据力的合成可得接触力N3与摩擦力Fμ的合力F3,LF3是F3对旋转中心O的力臂。
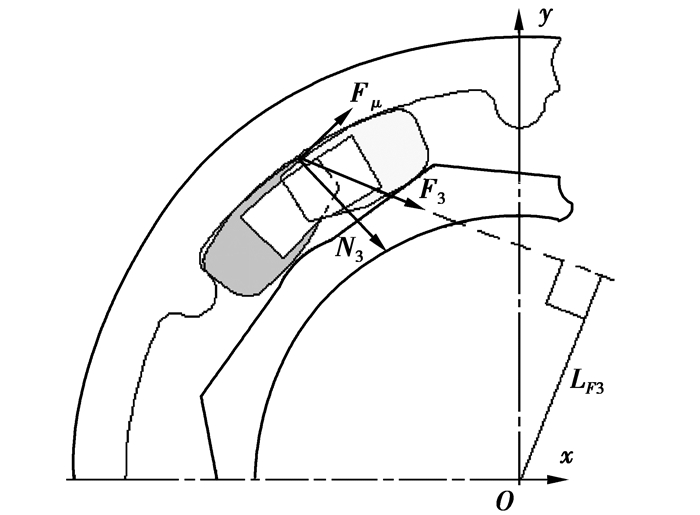
|
图 7 弹簧座楔入接触 |
由图 7知,弹簧座楔入接触以后,弹簧座接触曲面弹性变形引起的接触力以及摩擦力的作用,产生转矩T2=F3LF3,使双质量飞轮传递的转矩急剧增加。
综上所述,在弹簧座接触后的第2阶段,双质量飞轮传递的转矩为
| $ {T_3} = m\left( {{F_2}{L_f} + {F_3}{L_{{F_3}}}} \right) + {T_f}。$ | (10) |
双质量飞轮的扭转刚度
| $ {K_\theta } = {\rm{d}}T/{d_\alpha }。$ | (11) |
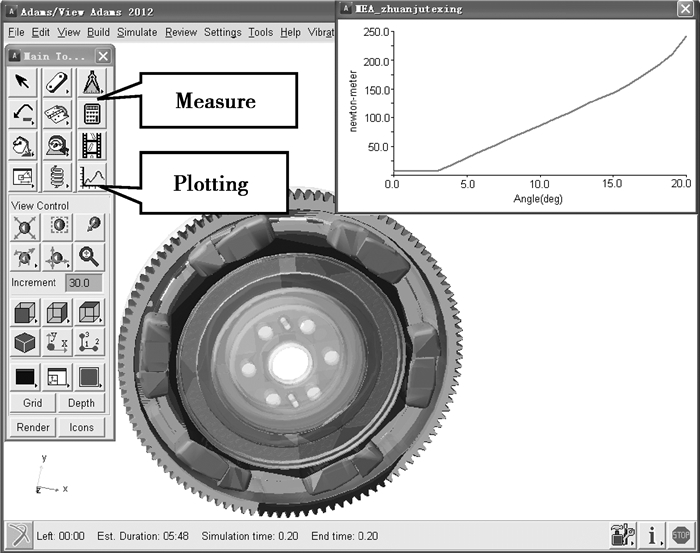
将双质量飞轮的三维实体导入ADAMS中,仿真模型如图 8所示。
|
图 8 边界条件和加载模型 1.弹簧座6与初级飞轮接触约束;2.弹簧座6与次级飞轮接触约束;3.初级飞轮上的固定副;4.次级飞轮上的旋转副;5.Translational Spring-Damper直弹簧;6.弹簧座4与初级飞轮接触约束;7.弹簧座4与次级飞轮接触约束;8.弹簧座4与弹簧座6接触约束 |
由于双质量飞轮上的零部件较多,为了简化模型,加快系统仿真速度,对于不参与运动分析的初、次级飞轮上的零部件利用布尔合运算合并到初、次级飞轮上。
坐标系建立在初级飞轮上,在初级飞轮的质心处添加一个固定副,在次级飞轮质心处添加一旋转副,使次级飞轮相对初级飞轮转动,并且在旋转副上加一常摩擦力矩来模拟摩擦阻尼轴承的作用。
采用Translational Spring-Damper并设置其弹簧线刚度来模拟弹簧座4、6之间弹簧的作用。弹簧座4、6的初始位置在初级飞轮的两凸缘之间,工作过程中,两个弹簧座的外表面和初级飞轮、次级飞轮的内壁面存在接触,当相对扭转角α至某一值时两弹簧座开始接触,相互摩擦楔入进而增大反抗转矩。故设置以下5对接触约束:弹簧座4与初级飞轮1、弹簧座4与次级飞轮2、弹簧座6与初级飞轮1、弹簧座6与次级飞轮2以及弹簧座4与弹簧座6接触。
在ADAMS-VIEW模块中为所建立的模型添加驱动,由于设置次级飞轮相对初级飞轮扭转转动,故将驱动伺服电机添加在次级飞轮的质心处,转速设为常数,边界条件和驱动的设置的模型如图 8所示。
设置好边界条件和驱动后,为了测量初级飞轮、次级飞轮在工作过程中传递的转矩随相对扭转角的变化规律,以初级相对于次级飞轮的扭转角α为自变量,通过Measure模块下的自定义函数功能将前述所建立的转矩特性数学模型以分段函数来表达输出转矩随扭转角α的变化,通过PostProcessor模块下的Plotting功能测量次级飞轮与弹簧座6接触约束下的传递转矩。
图 9所示为加载过程中弹簧座相互楔入接触过程,当相对扭转角达到16°时,两弹簧座头部开始接触并楔入,当相对扭转角达到20°时,弹簧座头部与根部接触,弹簧座完成楔入过程。

|
图 9 双质量飞轮加载过程中弹簧座的楔入 |
应用建立的双质量飞轮转矩特性计算模型对2.0L发动机搭载的双质量飞轮进行仿真分析计算,参数如下。
弹簧线刚度kt=7.441 N/mm,摩擦轴承转矩Tf=7 N·m,弹簧座材料为尼龙PA66,密度ρ1=1.15×103 kg/m3,泊松比υ1=0.28,弹性模量E1=8.3×103 MPa,初级飞轮、次级飞轮的材料为铸钢,密度ρ2=7.8×103 kg/m3,泊松比υ2=0.30,弹性模量E2=2.07×105 MPa,接触指数e=1.5,最大阻尼系数cmax=20 N·s/mm,弹性最大变形量d=0.01 mm,弹簧座与初级飞轮、次级飞轮之间的摩擦系数(有脂润滑)μ1=μ2=0.05,弹簧座相互楔入时的摩擦系数(有脂润滑)μ3=0.04,次级飞轮最大向径R1=106.1 mm,弹簧分布半径为R2=112.5 mm,顶角γ=139°,空转角θ=3°。
图 10为仿真分析的转矩特性曲线。其中水平直线段为转过空转角θ时由摩擦阻尼轴承产生的转矩,其后呈斜直线变化;当相对扭转角α≥16°,弹簧座相互楔入后的转矩特性曲线。由图知,楔入后双质量飞轮传递的转矩特性曲线非线性增加,进一步增大了反抗转矩。
|
图 10 仿真转矩特性曲线 |
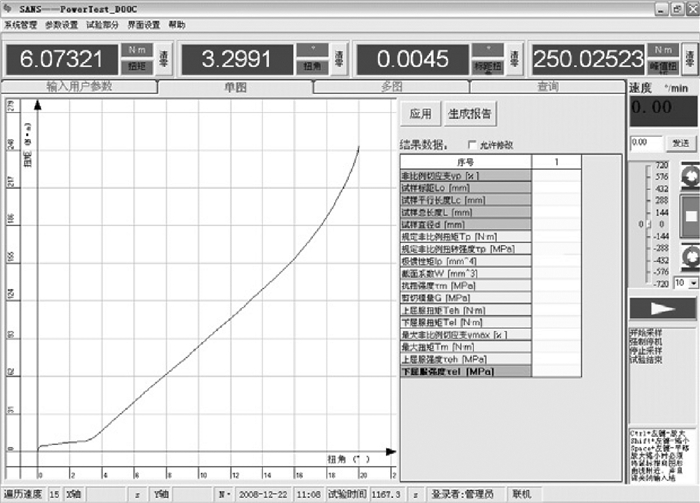
在重庆大学力学实验中心的电子扭转试验机上进行转矩扭转角试验,扭转角步长为0.1°/s,最大扭转角20°。试验设备如图 11所示,转矩试验曲线如图 12所示。

|
图 11 转矩扭转角台架试验 |
|
图 12 转矩试验曲线 |
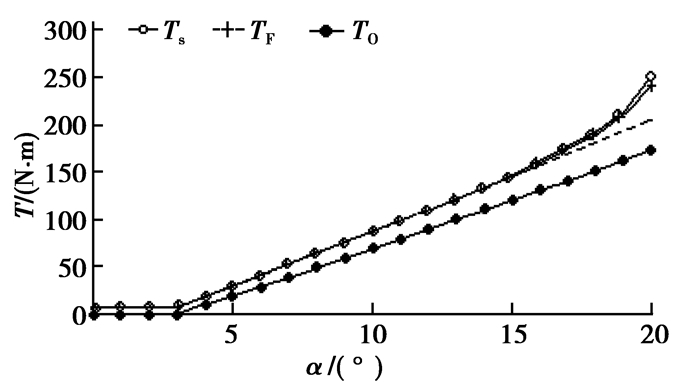
双质量飞轮转矩扭转角的仿真数据与试验数据列于表 1,转矩特性曲线绘制于图 13,其中,Ts为实际测试曲线,TF为仿真分析曲线,令摩擦系数μ1=μ2=0以及式(7)中Tf=0,得出不考虑摩擦的转矩曲线T0。
| 表 1 转矩转角测试与仿真数据 |
|
图 13 转矩特性曲线 |
当相对扭转角α≥16°时,两弹簧座头部开始接触并楔入,如图 9(a)所示在弹簧座间产生了正压力和摩擦力,使仿真曲线非线性急剧增大,与不考虑楔入的转矩曲线(图中虚线)相比,最大增幅近50 N·m。当相对扭转角α=20°时,弹簧座头部与根部接触,弹簧座完成楔入过程,由弹簧座的形状约束,弹簧不再被压缩,实现了对弹簧的过载保护,如图 9(b)所示。由表 1知,在扭转角α=20°处,仿真转矩数据(248.1 N·m)与测试转矩数据(251.3 N·m)相比,相对误差为1.3%,表明了仿真分析模型的正确性。
5 传动系统幅频特性与固有频率所搭载的汽车动力传动系统如图 1所示,发动机最大输出转矩为182 N·m,怠速转速为800 r/min,最高转速为7 000 r/min。
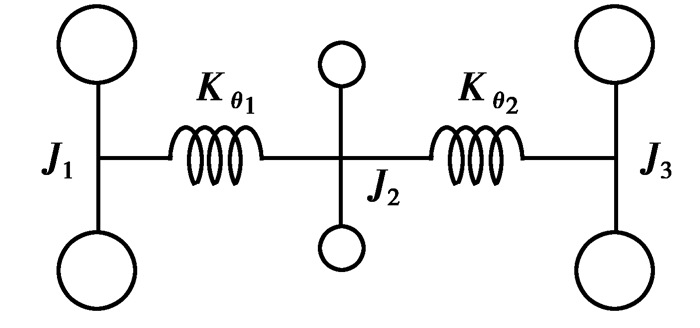
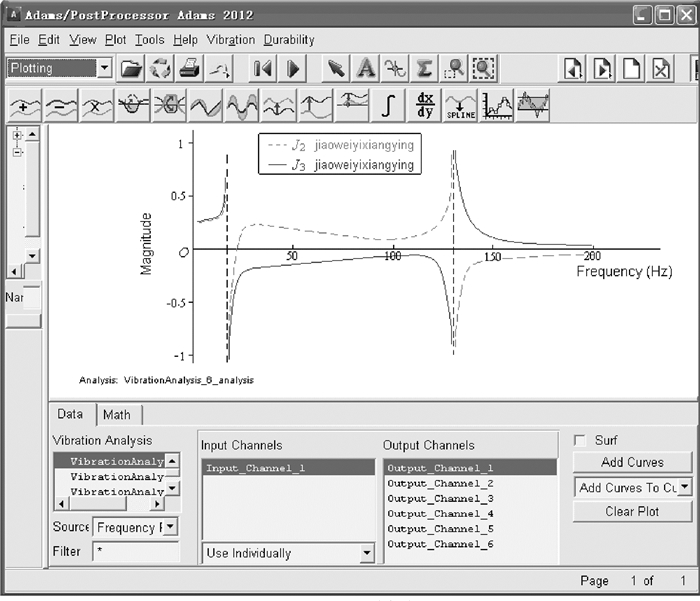
由于所关心的是系统的一、二阶固有频率,故在ADAMS的振动模块中将其简化为如图 14所示的三质量二自由度的质量弹簧系统。发动机曲轴1和初级飞轮2的等效转动惯量为J1=0.14 kg·m2,次级飞轮3及离合器4的等效转动惯量为J2=0.05 kg·m2,传动系统5的等效转动惯量为J3=2.06 kg·m2。在J1的质心处建立一个输入通道并施加正弦激励,在J2、J3的质心处分别建立角位移输出通道,双质量飞轮减振器扭转刚度斜直线段为Kθ1=11.7 N·m/(°),非线性阶段的扭转刚度在软件中由式(11)自行计算,传动系统的代换扭转刚度为Kθ2=556 N·m/(°)。设定起始频率为1 Hz,终止频率为200 Hz,对系统进行强迫振动分析,角位移的幅频特性曲线如图 15所示。
|
图 14 扭振分析模型 |
|
图 15 幅频特性曲线 |
由此获得传动系的一阶固有(共振)频率为f1=11.27 Hz,二阶固有(共振)频率为f2=130.45 Hz,其共振转速n1=676.2 r/min,n2=7 827 r/min。知n1小于发动机怠速转速,而n2大于发动机最高转速,搭载双质量飞轮的传动系统将共振完全隔离,提高了传动系零部件的寿命和车辆驾乘的舒适性。
6 结论1) 引入摩擦的双质量飞轮转矩特性分析模型更具真实性,利用摩擦特性,可以提高双质量飞轮的转矩。
2) 大扭转角时,弹簧座头部曲面间的摩擦楔入作用,能够大幅度提高反抗转矩,实现了低转速小扭转角的柔性和高转速大扭转角时非线性的大刚度高反抗转矩特性,且刚度连续无突变,避免了分段变刚度产生的冲击和噪声。
3) 试验表明,用所建立的转矩特性模型,并基于ADAMS进行仿真分析,是一种行之有效的方法,可方便地用于工程设计实践。
4) 对传动系搭载双质量飞轮的幅频特性与固有频率分析表明,双质量飞轮可以将共振转速完全有效地隔离在发动机的正常工作转速范围以外,从而改善了系统的固有特性,避免了共振现象的发生。
| [1] | Schaper U, Sawodny O, Mahl T, et al. Modeling and torque estimation of an automotive dual mass flywheel[C]//Proceedings of the 2009 American Control Conference, October 10-12, 2009, St. Louis, MO. Piscataway:IEEE Press, 2009:1207-1212. http://dl.acm.org/citation.cfm?id=1702514 |
| [2] | Walter A, Kiencke U, Jones S, et al. Cylinder balancing based on reconstructed engine torque for vehicles fitted with a dual mass flywheel(DMF)[J]. SAE International Journal of Passenger Cars-Electronic and Electrical Systems, 2009, 1(1): 810–819. |
| [3] | Theodossiades S, Gnanakumarr M, Rahnejat H, et al. Effect of a dual-mass flywheel on the impact-induced noise in vehicular powertrain systems[J]. Automobile Engineering, 2006, 220(6): 747–761. DOI:10.1243/09544070JAUTO55 |
| [4] | Kim J. Launching performance analysis of a continuously variable transmission vehicle with different torsional couplings[J]. Journal of Mechanical Design, 2005, 127(2): 295–301. DOI:10.1115/1.1814387 |
| [5] |
李伟, 史文库.
双质量飞轮(DMF)的研究综述[J]. 噪声与振动控制, 2008, 28(5): 1–5.
LI Wei, SHI Wenku. Summary of studies on dual mass flywheel(DMF)[J]. Noise and Vibration Control, 2008, 28(5): 1–5. (in Chinese) |
| [6] | Fidlin A, Seebacher R. DMF simulation techniques:finding the needle in the haystack[DB/OL].[2012-02-10]. http://www.yumpu.com/en/document/view/5921697/dmf-simulation-techniques-schaeffler-group. |
| [7] |
史文库, 龙岩, 卢玉东.
多级非线性双质量飞轮参数设计和优化[J]. 振动与冲击, 2009, 28(5): 92–96.
SHI Wenku, LONG Yan, LU Yudong. Parameter design and optimization of multistage nonlinear dual mass flywheel[J]. Journal of Vibration and Shock, 2009, 28(5): 92–96. (in Chinese) |
| [8] | Bach S H. Systematic search for and vibratory assessment of new action principles for alternative rotary vibration decoupling systems in the passenger car driveline[J]. Drive System Technique, 2004, 18(2): 3–12, 17, 24. |
| [9] |
宋立权, 李亮, 尹玉明, 等.
基于形状约束的双质量飞轮设计理论研究[J]. 机械工程学报, 2012, 48(1): 111–118.
SONG Liquan, LI Liang, YIN Yuming, et al. Study on design theory of dual mass flywheel based on shape constraint[J]. Chinese Journal of Mechanical Engineering, 2012, 48(1): 111–118. (in Chinese) |
| [10] |
张世义, 胡建军, 李光辉.
汽车动力传动系双质量飞轮式扭振减振器特性分析[J]. 现代制造工程, 2007(9): 120–124.
ZHANG Shiyi, HU Jianjun, LI Guanghui. Analyzed of characteristic for dual mass flywheel type torsional vibration damper of vehicle powertrain system[J]. Modern Manufacturing Engineering, 2007(9): 120–124. (in Chinese) |
| [11] |
江征风, 陈雷, 吴波.
双质量飞轮动态试验方法研究[J]. 武汉理工大学学报, 2008, 32(10): 117–119.
JIANG Zhengfeng, CHEN Lei, WU Bo. Research on method of dual mass fly-wheel dynamic experimentation[J]. Journal of Wuhan University of Technology, 2008, 32(10): 117–119. (in Chinese) |
| [12] |
徐中明, 张玉峰, 余烽, 等.
可变阻尼减振器外特性仿真与试验[J]. 重庆大学学报, 2010, 33(9): 29–34.
XU Zhongming, ZHANG Yufeng, YU Feng, et al. External characteristics simulation and experiment of variable-damping shock absorbers[J]. Journal of Chongqing University, 2010, 33(9): 29–34. DOI:10.11835/j.issn.1000-582X.2010.09.006 (in Chinese) |
| [13] | Kang T S, Kauh S K, Ha K P. Development of the displacement measuring system for a dual mass flywheel in a vehicle[J]. Journal of Automobile Engineering, 2009, 223(10): 1273–1281. DOI:10.1243/09544070JAUTO1066 |
| [14] | Kodama T, Wakabayashi K, Honda Y, et al. An experimental study on dynamic characteristics of torsional stiffness and torsional damping coefficient of vision-friction dampers[J]. Transactions of the Kokushikan University Department of Engineering, 2001(34): 67–79. |
| [15] |
吕振华, 吴志国, 陈涛.
双质量飞轮周向短弹簧型扭振减振器弹性特性设计原理及性能分析[J]. 汽车工程, 2003, 25(5): 493–497.
Lü Zhenhua, WU Zhiguo, CHEN Tao. The design principles and performance analysis of DMF-CSS torsional damper[J]. Automotive Engineering, 2003, 25(5): 493–497. (in Chinese) |
| [16] |
宋立权, 赵孝峰, 何泽海, 等.
引入摩擦的周向短弹簧汽车双质量飞轮分析模型及扭振固有特性研究[J]. 机械工程学报, 2009, 45(11): 99–105.
SONG Liquan, ZHAO Xiaofeng, HE Zehai, et al. Analysis modal and inherent characteristics of torsional vibration of the dual mass flywheel-circumferential short spring introduced friction[J]. Journal of Mechanical Engineering, 2009, 45(11): 99–105. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

