功率超声振动珩磨加工以珩磨力小、珩磨温度低等优异性能被应用于汽车、坦克发动机等内燃机缸套的精密加工,但由于超声振动加工系统内在因素的作用会产生自激振动,从而影响缸套的加工表面质量[1]。很多学者[2-4]对机床加工颤振进行了深入的研究,Ahmadi等[5]考虑了非线性阻尼对切削系统稳定性极限图的影响,并且给出了非线性系统稳定性边界条件;Weng等[6]建立了磨削动力学模型,研究了不同磨削参数对磨削颤振和表面波纹的影响;黄强等[7]通过颤振能量补充和质量效应角度得出颤振发生于工件系统和刀具系统这两个最终执行部件之一。
大多数学者只是针对铣削、磨削等加工系统进行了颤振的稳定性分析,对于珩磨加工这种特殊的加工方式,特别是当珩磨油石上施加超声振动后,其系统珩磨颤振机理有其特有的规律。笔者基于再生型颤振理论对功率超声振动珩磨颤振系统进行了稳定性分析,并通过试验研究探讨了有效防止超声珩磨过程中颤振产生的加工参数和系统参数的合理选择。
1 超声珩磨颤振系统动力学模型建立 1.1 超声珩磨动态珩磨力模型建立普通珩磨加工过程中,珩磨力起源于油石磨粒与工件划擦、耕梨、切削后引起工件材料弹塑性变形、磨屑形成以及油石磨粒和结合剂与工件表面之间的摩擦作用[8],其大小和变化规律严重影响油石磨耗、珩磨热、工件表面质量,甚至会造成珩磨系统的自激振动,是表征珩磨加工质量的重要参数。
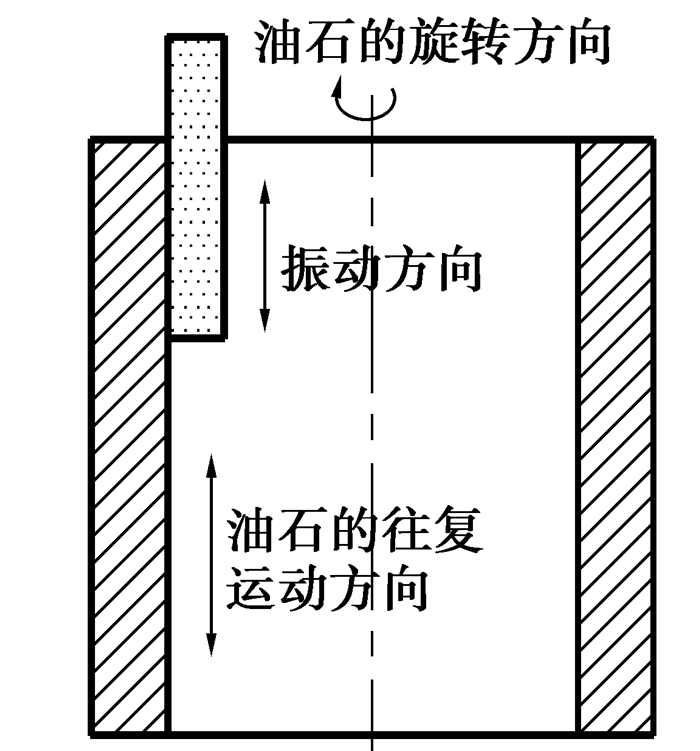
超声珩磨加工过程更加复杂,油石磨粒在受到普通珩磨力的基础上还受到超声振动脉冲力的作用[9-10]。根据珩磨油石施加超声振动方向的不同,可分为轴向振动、径向振动和扭转振动,本课题主要对轴向振动珩磨油石进行分析,如图 1所示,油石在轴向旋转和往复运动的同时作超声频的轴向振动[11]。假设附加在珩磨油石上的超声振动位移为正弦波形式,初相位为零,则油石轴向超声振动位移为
| $ y = A\sin \;2\pi ft, $ | (1) |
|
图 1 油石施加轴向超声振动的珩磨加工 |
式中:A为超声振动振幅,μm;f为超声振动频率,Hz。
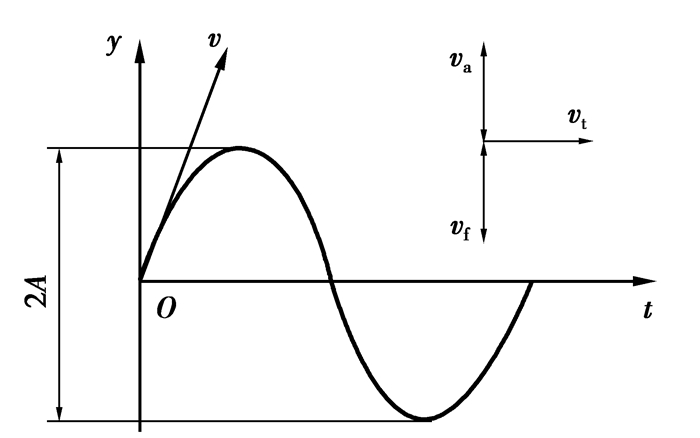
根据功率超声珩磨运动学原理,可以得出超声珩磨过程中单颗磨粒的运动速度合成如图 2所示[12],其中v为轴向超声振动合成速度,m/s;vt=πdn为珩磨圆周速度,m/s;±va为油石往复运动速度,vf=y′=2πAf cos 2πft为油石超声振动速度;d为工件内径;n为主轴转速。
|
图 2 单颗磨粒轴向超声振动运动速度合成 |
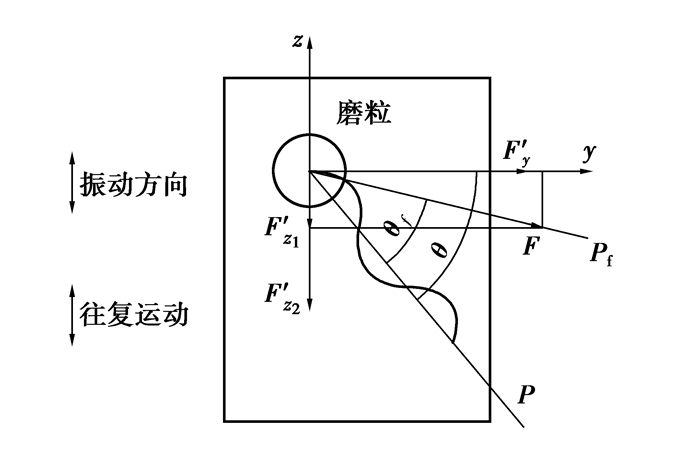
将珩磨工件内孔展开,假设油石磨粒为顶角是2φ的圆锥,且在油石表面均匀等高分布,可以得到单颗磨粒的受力分析如图 3所示,其中,Pf方向为油石磨粒在超声振动下的运动合成速度方向;P方向为相同条件下磨粒在没有加超声振动时的运动速度方向;F′z1为普通珩磨时,单颗磨粒轴向珩磨力大小;F′z2为超声珩磨过程中油石单颗磨粒受到的超声脉冲力;F′y为单颗磨粒在y轴方向上的珩磨力;F为施加超声振动后,总的珩磨力大小。珩磨加工时,工件加工表面会留下特有的珩磨网纹,结合图 2磨粒运动速度分析可以计算出Pf方向与P方向之间的夹角θf=arctan((va+vf)/vt),P方向与y轴的夹角,即珩磨网纹角半角θ=arctan(va/vt)。
|
图 3 超声振动珩磨时单颗磨粒受力图 |
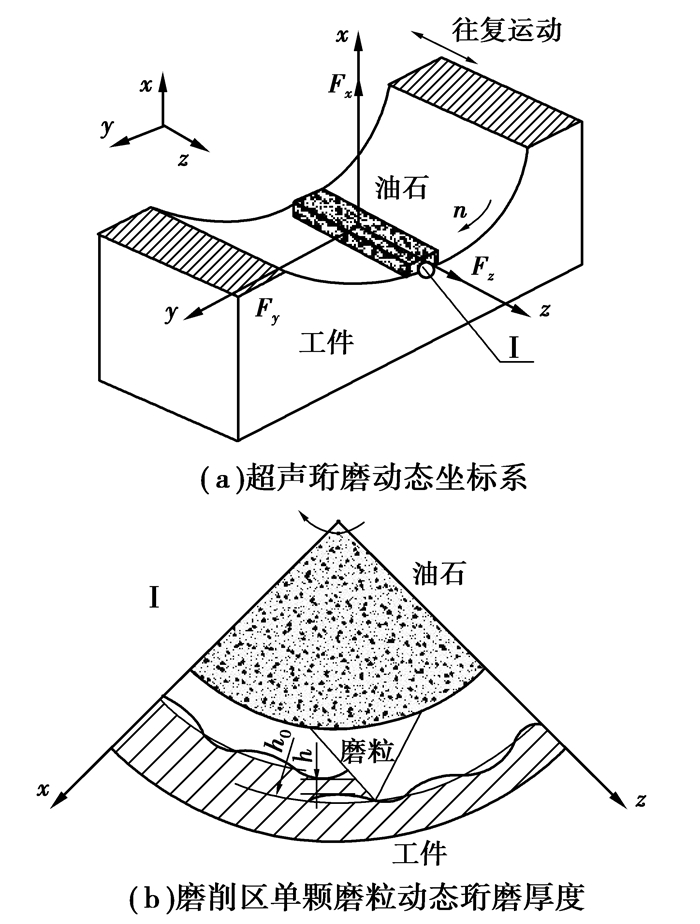
超声振动珩磨过程中,再生型颤振是一种典型的由于振动位移延时反馈而导致的动态失稳现象,而动态珩磨厚度的变化将直接影响动态珩磨力的大小[13]。这里只考虑单颗磨粒在x和z方向珩磨厚度变化引起的自激振动,如图 4所示为超声珩磨的空间坐标系xyz,其中n为主轴转速,Fx、Fy、Fz分别为珩磨油石径向、周向和轴向珩磨力;图 4(b)为微观尺度下单颗磨粒动态珩磨厚度示意图,图中h0为理论珩磨厚度,h为动态珩磨厚度。
|
图 4 超声珩磨动态珩磨厚度示意图 |
根据图 3中超声珩磨加工的特征,建立功率超声珩磨加工中油石的动态珩磨厚度为
| $ h = \left( {\theta, t} \right) = \Delta x\;\cos \left( {\theta-{\theta _{\rm{f}}}} \right){\rm{ + }}\Delta z\sin \left( {\theta-{\theta _{\rm{f}}}} \right), $ | (2) |
式中:Δx和Δz分别为磨粒在x轴和z轴方向上的动态位移;θ为珩磨网纹半角;θf为施加超声和未施加超声时磨粒合成运动速度夹角。
超声珩磨加工过程中,作用在油石条上的动态珩磨力与油石动态珩磨厚度和珩磨宽度成正比,假设油石磨粒与工件为线性接触,且接触轴线上的有效磨粒数均匀等高分布,则整个油石条在x(径向)和z(轴向)方向上的动态珩磨力为
| $ {F_x} = {K_{\rm{t}}}abh\left( {\theta, t} \right)/l, $ | (3) |
| $ {F_z} = {K_{\rm{a}}}{K_{\rm{t}}}abh\left( {\theta, t} \right)/l + {F_{\rm{f}}}, $ | (4) |
式中:Kt、Ka分别为磨粒的径向和轴向珩磨力系数,N/mm;b为油石宽度,mm;a为油石珩磨长度,mm;l为相邻两颗磨粒之间的平均宽度,mm;Ff=-4π2Af2msin 2πft为超声珩磨轴向脉冲力,其中m是珩磨油石的等效质量。
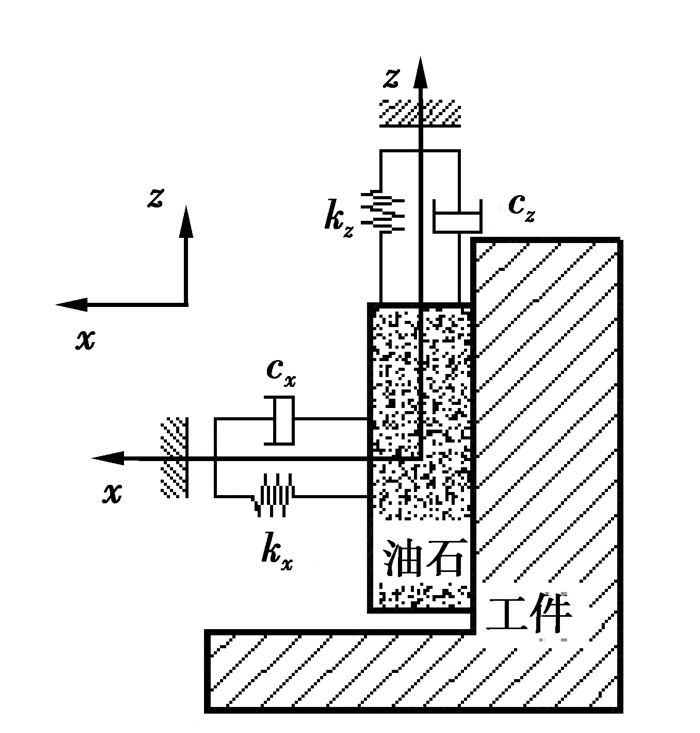
1.2 超声珩磨颤振系统动力学模型建立超声振动珩磨加工过程中,珩磨油石与工件之间的再生效应是引起超声振动珩磨颤振现象的主要原因,在不考虑振型耦合和负摩擦效应的影响下,建立超声振动珩磨颤振的动力学模型如图 5所示[14]。
|
图 5 超声珩磨颤振两自由度系统模型 |
根据图 5建立的超声振动珩磨颤振系统模型,将油石简化为x、z方向的弹簧阻尼系统,可以得到油石颤振系统的运动微分方程为
| $ {m_x}\ddot x\left( t \right) + {c_x}\dot x\left( t \right) + {k_x}x\left( t \right) = {F_x}\left( t \right), $ | (5) |
| $ {m_z}\ddot z\left( t \right) + {c_z}\dot z\left( t \right) + {k_z}z\left( t \right) = {F_z}\left( t \right), $ | (6) |
式(5)、(6)分别为径向(x)和轴向(z)油石颤振的动力学微分方程,其中,mx、mz,cx、cz,kx、kz分别为油石x、z方向的等效质量、等效阻尼和等效刚度。
2 超声珩磨颤振系统的稳定性分析 2.1 超声珩磨颤振系统稳定性方程建立研究超声振动珩磨颤振系统中,由超声波产生的脉冲力是由外力引起的,它只对超声珩磨系统的强迫振动产生激振作用,而对系统的再生型颤振不起作用,因此分别对油石的振动微分方程(5)、(6)进行拉式变换得到
| $ {s^2}x\left( s \right) + 2{\xi _x}{\omega _{{\rm{n}}x}}sx\left( s \right) + \omega _{{\rm{n}}x}^2x\left( s \right) = {F_x}\left( s \right)/{m_x}, $ | (7) |
| $ {s^2}z\left( s \right) + 2{\xi _z}{\omega _{{\rm{n}}z}}sz\left( s \right) + \omega _{{\rm{n}}z}^2z\left( s \right) = {F_z}\left( s \right)/{m_z}。$ | (8) |
超声珩磨颤振系统的传递函数为超声珩磨系统输出位移与珩磨系统对应方向上所受激振力的拉式变换之比,根据控制工程理论,颤振系统稳定性主要取决于时域特性上传递函数根的性质,假设传递函数复数根s=iωc,则超声珩磨颤振系统的传递函数
| $ \mathit{\boldsymbol{G}}\left( {i{\omega _{\rm{c}}}} \right) = \left[\begin{array}{l} {G_{xx}}\left( {i{\omega _{\rm{c}}}} \right)\;\;\;\;\;\;\;0\\ \;\;\;\;0\;\;\;\;\;\;\;\;\;{G_{zz}}\left( {i{\omega _{\rm{c}}}} \right) \end{array} \right]。$ | (9) |
根据超声珩磨颤振系统传递函数意义,可以通过动态珩磨力来表示相应方向上的颤振位移输出,假设系统动态珩磨力为Feiωct,则超声珩磨系统的位移输出为
| $ \left[\begin{array}{l} \Delta x\left( {i{\omega _{\rm{c}}}} \right)\\ \Delta z\left( {i{\omega _{\rm{c}}}} \right) \end{array} \right] = \left( {1 - {e^{ - i{\omega _{\rm{c}}}T}}} \right)\left[{\mathit{\boldsymbol{G}}\left( {i{\omega _{\rm{c}}}} \right)} \right]\mathit{\boldsymbol{F}}{{\rm{e}}^{i{\omega _{\rm{c}}}t}}。$ | (10) |
将式(10)带入到动态珩磨力表达式中,整理可以得到超声珩磨颤振系统的矩阵方程表达式为
| $ \mathit{\boldsymbol{I}}-{K_t}\frac{a}{l}b\left( {1-{e^{-i{\omega _c}T}}} \right)\mathit{\boldsymbol{A}}\left( t \right)\mathit{\boldsymbol{G}}\left( {i{\omega _{\rm{c}}}} \right) = 0, $ | (11) |
式中
研究颤振系统稳定性的目的是为了得到有效控制颤振产生的加工参数[15],利用稳定性极限图能够方便得到影响颤振系统的主要参数及其相互关系。超声珩磨颤振系统中,主要通过计算珩磨宽度和主轴转速的关系来研究珩磨过程中颤振稳定性条件。
令
| $ {b_{\lim }} =-\frac{{l{\mathit{\Theta }_0}}}{{2{K_{\rm{t}}}a}}\left( {1 + {{\left( {\frac{{{\mathit{\Theta }_1}}}{{{\mathit{\Theta }_2}}}} \right)}^2}} \right), $ | (12) |
式中Θ1(1-cos ωcT)-Θ0sin ωcT=0。
可以得到超声珩磨颤振系统稳定性方程特征值的相位移γ=arctan(Θ1/Θ0),假设系统颤振频率为ωc,k为超声珩磨过程中磨削圆弧留下的颤振波纹倍数,即稳定性极限图中的叶瓣数,则有ωcT=π-2γ+2kπ,根据珩磨头的主轴转速n与珩磨油石磨削周期T关系,可以得到主轴转速为
| $ n = \frac{{60{\omega _{\rm{c}}}}}{{\left( {2k + 1} \right)\pi-2{\rm{aectan}}\left( {{\mathit{\Theta }_1}/{\mathit{\Theta }_\mathit{0}}} \right)}}。$ | (13) |
根据以上分析可以得知,超声珩磨极限珩磨宽度blim和珩磨头主轴转速n分别为k和颤振频率ωc的函数,给出超声振动珩磨系统及加工参数就可以绘制出超声珩磨颤振稳定性极限图。
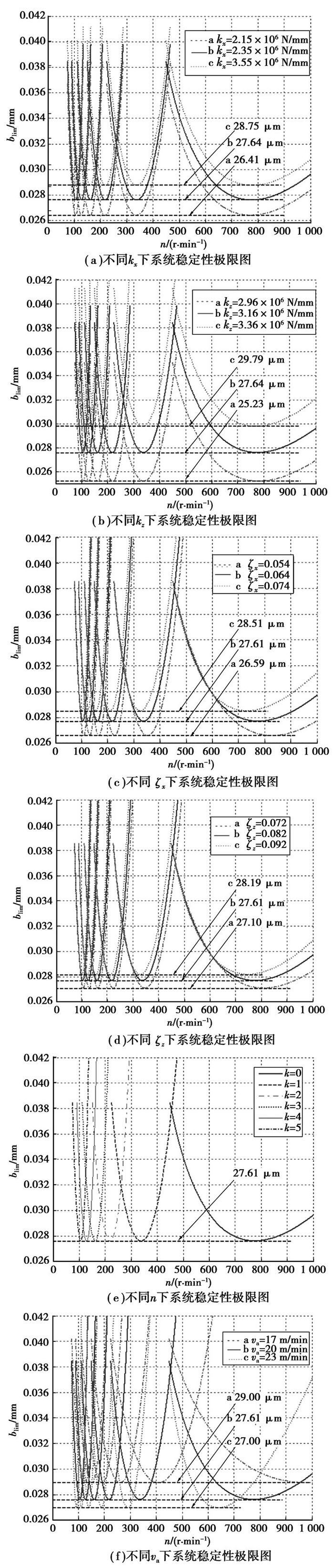
2.2 功率超声珩磨颤振系统稳定性仿真根据建立的超声珩磨颤振的稳定性方程(式(12)、(13)),可以得出各系统和加工参数下系统稳定性极限图(如图 6)。
|
图 6 不同系统结构和加工参数对系统稳定性极限图的影响 |
从图 6可以看出主轴转速对颤振系统的最小极限珩磨宽度影响不大,但是主轴转速小于400 r/min时,系统的临界稳定区域较小,容易发生颤振;从图 6(a)~(d)可以看出系统刚度与阻尼比系数对系统稳定性影响类似,提高系统刚度和阻尼比系数均会提高系统稳定性;从图 6(f)可以看出往复速度为23 m/min时,临界珩磨宽度减小到27 μm,系统不稳定磨削区域增大,容易出现颤振。
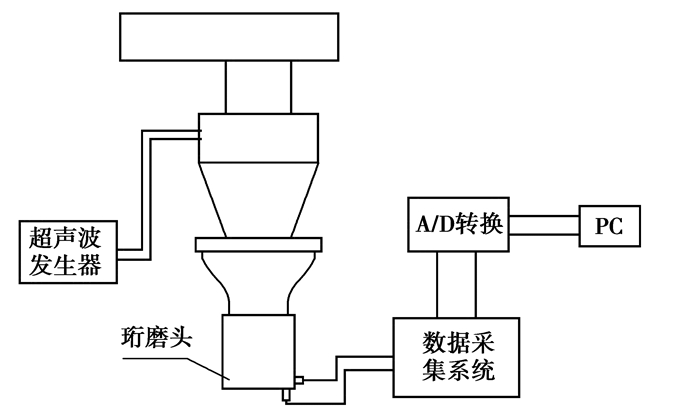
3 超声珩磨稳定性试验分析利用自行研制的ϕ47 mm功率超声珩磨装置在MBA4215型半自动立式珩磨机对材料为38CrMnA的缸套(ϕ47 mm×ϕ90 mm×75 mm)进行试验,并且通过安装在珩磨头体的加速度传感器对不同珩磨参数下加速度信号进行采集,应用A/D转换器对加速度数据进行处理,得出珩磨头体在加工过程中径向和轴向的振动信号时域图,从而对加工过程的稳定性进行判断,实验装置原理示意图如图 7所示。
|
图 7 超声珩磨稳定性试验原理图 |
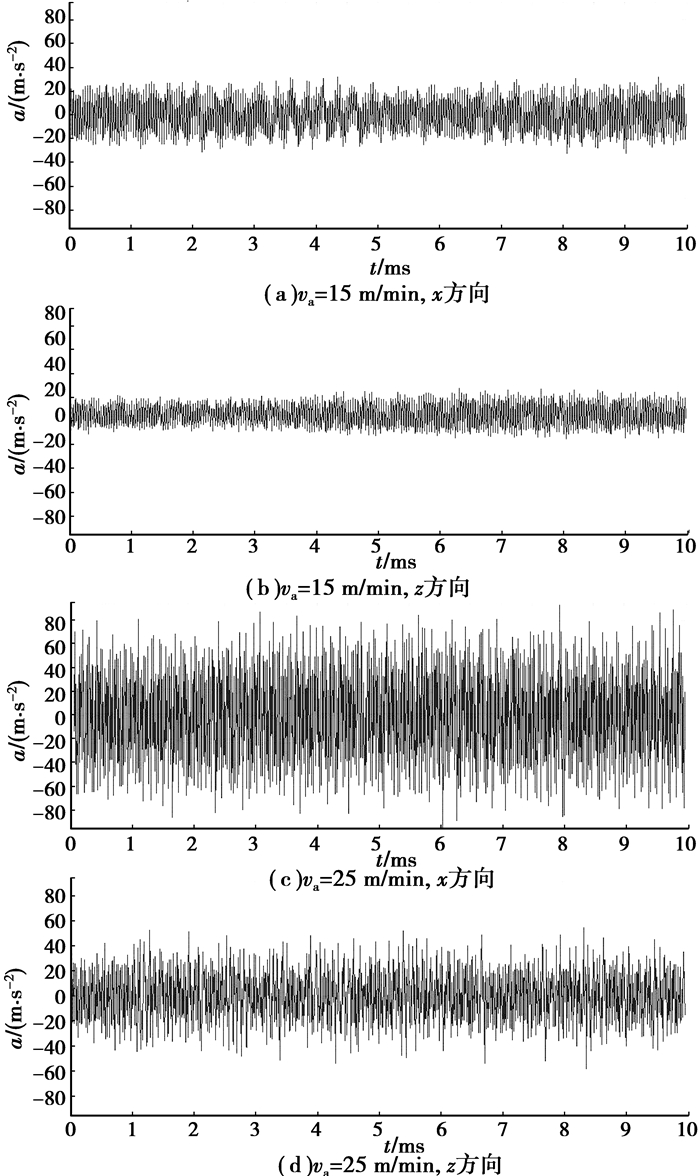
在主轴转速为315 r/min,珩磨厚度为20 μm,其他加工参数不变,珩磨头往复速度分别为15和25 m/min时,得到的振动时域图如图 8所示,其中横坐标为时间(ms),纵坐标为加速度值(m/s2)。
|
图 8 不同主轴转速下系统x和z方向的振动信号图 |
从图 8可以看出其他参数不变的情况下,往复珩磨速度从15 m/min提高到25 m/min时,系统在径向和轴向的加速度信号出现明显的振幅增大的情况,超声珩磨加工系统出现不稳定的颤振现象,并且在实验现场可以听到明显刺耳的声音,对比两种加工条件下工件表面形貌也可以得到证明,如图 9所示。从图 9(a)中可以看出在低往复速度下,工件表面是正常的珩磨网纹,图 9(b)显示在高往复速度下工件表面出现颤振波纹,也证明了理论部分的正确性,结合理论仿真结果可以得到珩磨宽度为27 μm时,超声珩磨系统出现颤振。

|
图 9 不同珩磨头往复速度下工件表面形貌 |
通过对建立的功率超声珩磨颤振系统动力学模型的稳定性分析,可以得出以下结论:
1) 主轴转速对超声振动珩磨颤振系统的稳定性有显著影响,当主轴转速低于400 r/min时,系统稳定性区域减小,容易发生颤振。
2) 通过珩磨头往复速度的单因素试验,可以得到超声珩磨发生颤振的临界珩磨宽度为27 μm。
3) 系统刚度与系统阻尼比系数对极限珩磨宽度的影响类似,基本成正比关系,为避免颤振的发生,应当增大系统刚度和系统阻尼比系数。
| [1] |
祝锡晶, 王爱玲, 辛志杰, 等.
功率超声珩磨缸套加工中谐振系统的试验研究[J]. 中国机械工程, 2002, 13(9): 727–730.
ZHU Xijing, WANG Ailing, XIN Zhijie, et al. Study on the vibration system of the efficiency ultrasonic cylinder honing[J]. China Mechanical Engineering, 2002, 13(9): 727–730. (in Chinese) |
| [2] | Dassanayake A V, Suh C S. On nonlinear cutting response and tool chatter in turning operation[J]. Communications in Nonlinear Science and Numerical Simulation, 2008, 13(5): 979–1001. DOI:10.1016/j.cnsns.2006.08.003 |
| [3] | Moradi H, Bakhtiari-Nejad F, Movahhedy M R, et al. Nonlinear behavior of the regenerative chatter in turning process with a worn tool:forced oscillation and stability analysis[J]. Mechanism and Machine Theory, 2010, 45(8): 1050–1066. DOI:10.1016/j.mechmachtheory.2010.03.014 |
| [4] | Adetoro O B, Sim W M, Wen P H. An improved prediction of stability lobes using nonlinear thin wall dynamics[J]. Journal of Materials Processing Technology, 2010, 210(6/7): 969–979. |
| [5] | Ahmadi K, Ismail F. Analytical stability lobes including nonlinear process damping effect on machining chatter[J]. International Journal of Machine Tools and Manufacture, 2011, 51(4): 296–308. DOI:10.1016/j.ijmachtools.2010.12.008 |
| [6] | Weng Z Y, Xie W D, Lu B, et al. Grinding chatter and ground surface waviness in surface grinding process[J]. Key Engineering Materials, 2004, 259/260: 352–356. DOI:10.4028/www.scientific.net/KEM.259-260 |
| [7] |
黄强, 张根保, 张新玉, 等.
机床颤振过程的试验与分析[J]. 重庆大学学报, 2008, 31(4): 360–364, 370.
HUANG Qiang, ZHANG Genbao, ZHANG Xinyu, et al. The chatter vibration process of machine tools[J]. Journal of Chongqing University, 2008, 31(4): 360–364, 370. DOI:10.11835/j.issn.1000-582X.2008.04.002 (in Chinese) |
| [8] |
张建华, 葛培琪, 张磊, 等.
基于概率统计的磨削力研究[J]. 中国机械工程, 2007, 18(20): 2399–2402.
ZHANG Jianhua, GE Peiqi, ZHANG Lei, et al. Research on the grinding force based on the probability statistics[J]. China Mechanical Engineering, 2007, 18(20): 2399–2402. DOI:10.3321/j.issn:1004-132x.2007.20.002 (in Chinese) |
| [9] | Zhu X J, Wang J Q, Cheng Q, et al. Radial power ultrasonic vibration honing friction analysis[J]. Solid State Phenomena, 2011, 175: 183–186. DOI:10.4028/www.scientific.net/SSP.175 |
| [10] |
王建青, 邵延君, 祝锡晶.
轴向功率超声振动珩磨的运动学分析[J]. 现代制造工学, 2010(1): 60–62.
WANG Jianqing, SHAO Yanjun, ZHU Xijing. Kinematics analysis on power ultrasonic vibration honing along axial direction[J]. Modern Manufacturing Engineering, 2010(1): 60–62. (in Chinese) |
| [11] | 王爱玲, 祝锡晶, 吴秀玲. 功率超声振动加工技术[M]. 北京: 国防工业出版社, 2007. |
| [12] | Wang J Q, Zhu X J, Cheng Q, et al. Analysis of ultrasonic honing chatter vibration trajectory[J]. Advanced Materials Research, 2010, 135: 79–83. DOI:10.4028/www.scientific.net/AMR.135 |
| [13] | Hecker R L, Liang S Y, Wu X J, et al. Grinding force and power modeling based on chip thickness analysis[J]. The International Journal of Advanced Manufacturing Technology, 2007, 33(5/6): 449–459. |
| [14] | Zhu X J, Wang J Q, Chen Q, et al. Research on dynamic grinding force in ultrasonic honing chatter[J]. Key Engineering Materials, 2011, 487: 433–437. DOI:10.4028/www.scientific.net/KEM.487 |
| [15] | Nayfeh A H, Nayfeh N A. Analysis of the cutting tool on a lathe[J]. Nonlinear Dynamics, 2011, 63(3): 395–416. DOI:10.1007/s11071-010-9811-6 |
 2013, Vol. 36
2013, Vol. 36



