软磁材料进行磁化后,其形状或大小发生变化的现象,即为磁致伸缩效应或威德曼效应。这是磁致伸缩位移传感器弹性波的产生的基础。因此,与基于其他原理的传感器不同[1-2],只有磁致伸缩位移传感器才能实现非接触测量,这种明显优势使其被广泛应用于航天、石油、化工等工业领域[3]。
目前公开报道的磁致伸缩位移传感器(MDS)的波导丝大多由饱和磁致伸缩系数(λs)不足3×10-5的Fe-Ni合金制成,此类MDS的位移检测量不超过5 m[4]。虽然有些超磁致伸缩材料的λs超过1×10-3,但它们基本上都是烧结类材料,不能制备为波导丝,因此无法应用于MDS[5]。
21世纪以来,Clark提出Fe83Ga17材料在特殊的制备工艺条件下,其λs可以达到4×10-4[6],虽然比烧结类材料的λs小得多,但比现有Fe-Ni材料磁致伸缩性能优越,而且再加工性能良好。近期,李纪恒对Fe83Ga17波导丝的威德曼效应进行了研究,得到高达245 s/cm的扭转角,在材料学上说明了其优越性[7]。
为此,在对比前期研究的基础上[8-9],提出将Fe83Ga17材料应用于大位移磁致伸缩位移传感器。由于MDS波导丝的效果不仅取决于它的λs和威德曼扭转角,还与其磁场特性密切相关。因此,笔者在掌握MDS原理,建立Fe83Ga17波导丝磁场模型的基础上,利用MATLAB对其磁场特性进行了分析,并最终结合检测到的信号特性证明了Fe83Ga17材料应用于大位移MDS的可行性。
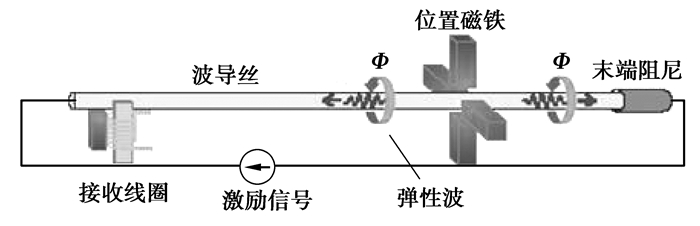
1 MDS原理磁致伸缩位移传感器如图 1所示。波导丝在激励电流作用下产生的环形磁场Фi和永磁铁产生的稳恒磁场Фm相交时,便会瞬间合成一个螺旋形的扭转磁场Ф,根据磁致伸缩材料的威德曼效应,波导丝将会产生瞬间形变,由此形成一个向两端传播的扭转弹性波。
|
图 1 MDS工作原理 |
当接收线圈检测到扭转弹性波时,其磁通量强度B会发生相应变化。根据Villari效应,在检测线圈上将能够检测到感应电压,如式(1)所示。
| $ e = - NS\frac{{{\rm{d}}B}}{{{\rm{d}}t}}, $ | (1) |
其中:e为感应电压;N为线圈匝数; S为线圈的截面面积; B为磁感强度。
假设从永磁铁到线圈的传输时间为t,超声波的传输速度为v,线圈和磁铁之间的距离L就可以用式(2)计算得到,从而实现位移的测量。
| $ L = vt。$ | (2) |
在建立磁场模型分析之前,需要确定激励信号和波导丝的参数以及波导丝的B-H特性。
大量实验表明,激励信号为脉冲电流时威德曼效应最佳,作者在先前的工作中已经进行了大量研究[8-9],相关参数如表 1所示。
| 表 1 激励电流参数 |
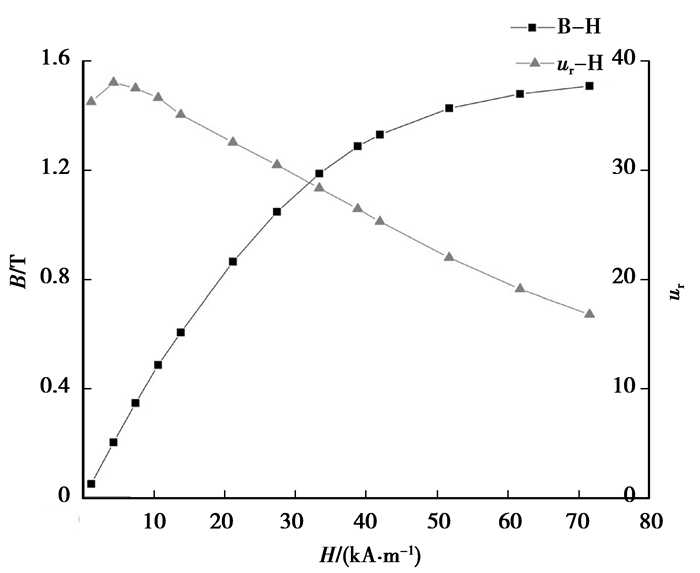
波导丝的B-H特性曲线如图 2所示。它直接影响着磁场特性的强弱和威德曼效应的效果,并对磁致伸缩位移传感器量程的改善起着决定性作用。
|
图 2 Fe83Ga17波导丝的特性曲线 |
在一般的磁场模型分析中,可以直接利用安培环路定理来得出相关模型的磁场特性分布。但是,由于作用于波导丝的激励源并不是稳恒电流,而是脉冲电流,因此,并不能利用安培环路定理来对其进行分析。为了对波导丝在激励电流作用下产生的磁场特性进行数学分析,笔者首先利用信号与系统的傅里叶级数理论,将周期脉冲电流信号转换成一系列电磁学分析中常见的正弦电流信号,然后利用叠加原理将正弦电流信号产生时谐场进行叠加,从而得到所需要的磁场模型。
3.1 信号转换设激励电流I(t)的脉宽为τ,幅度为A,周期为T。为了方便分析,选取电流信号中任意脉冲的中点时刻为参考零时刻。
由此可知,I(t)的数学描述为
| $ I\left( t \right) = \sum\limits_{l = - \infty }^{l = \infty } {i\left( {t - lT} \right)} , $ | (3) |
式中,参考中心的单位脉冲i(t)为
| $ i\left( t \right) = A\left[ {u\left( {t + \frac{\tau }{2}} \right) - u\left( {t - \frac{\tau }{2}} \right)} \right], $ | (4) |
由于I(t)满足狄里克雷条件,因此I(t)以三角形式的傅里叶级数表示为
| $ I\left( t \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^{n = + \infty } {\left[ {{a_n}\cos \left( {nwt} \right) + {b_n}\sin \left( {nwt} \right)} \right]} , $ | (5) |
其中傅里叶级数系数分别为
| $ {a_0} = \frac{2}{T}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {I\left( t \right){\rm{d}}t} = \frac{2}{T}\int_{ - \frac{\tau }{2}}^{\frac{\tau }{2}} {A{\rm{d}}t} = \frac{{2A\tau }}{T}, $ | (6) |
| $ \begin{array}{l} {a_n} = \frac{2}{T}\int_{ - \frac{T}{2}}^{\frac{T}{2}} {I\left( t \right){\rm{cos}}\left( {nwt} \right){\rm{d}}t} = \\ \;\;\;\;\;\;\;\frac{2}{T}\int_{ - \frac{\tau }{2}}^{\frac{\tau }{2}} {A\cos \left( {\frac{{2{\rm{ \mathsf{ π} }}nt}}{T}} \right){\rm{d}}t} = \\ \;\;\;\;\;\;\;\frac{{2A}}{{n{\rm{ \mathsf{ π} }}}}\sin \left( {\frac{{n{\rm{ \mathsf{ π} }}\tau }}{T}} \right) = \frac{{2A\tau }}{T}\sin c\left( {\frac{{n\tau }}{T}} \right), \end{array} $ | (7) |
因为I(t)是偶函数,所以正弦分量为零,即
| $ {b_n} = 0, $ | (8) |
于是,激励电流的傅里叶分解形式为
| $ \begin{array}{l} I\left( t \right) = \frac{{A\tau }}{T} + \frac{{2A\tau }}{T}\sum\limits_{n = 1}^{n = + \infty } {\sin {\rm{c}}\left( {\frac{{n\tau }}{T}} \right)\cos \left( {nwt} \right)} = \\ \;\;\;\;\;\;\;\;\;\;I' + \sum\limits_{n = 1}^{n = + \infty } {\sqrt 2 {I_n}\cos \left( {{w_n}t} \right)} 。\end{array} $ | (9) |
由式(9)可知,激励电流可以分解为一个直流信号和一系列不同频率的正弦信号。
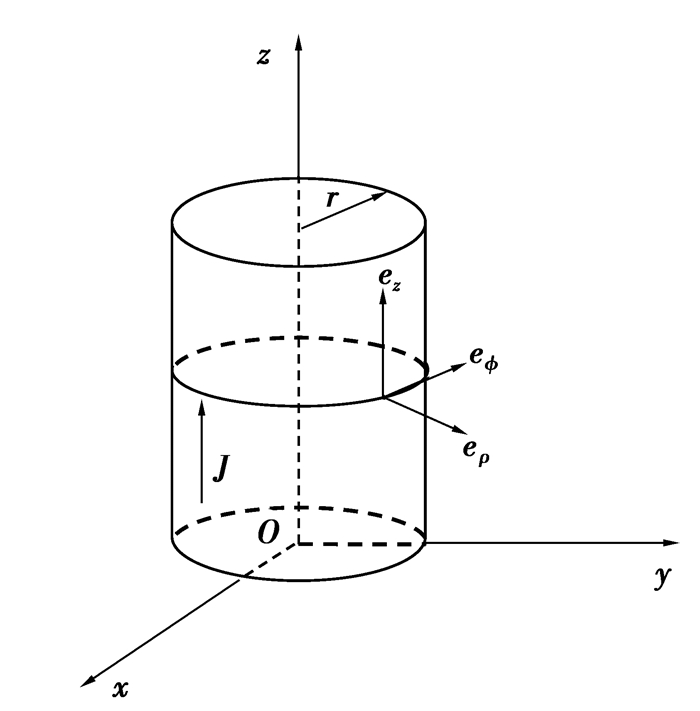
3.2 分析直流分量磁场特性在对磁致伸缩波导丝的几何结构进行分析时,可将其看成半径为r的长直圆柱,分析稳恒电流信号对波导丝的作用,可将其看成圆柱体内通过电流为I′的直流信号,为了便于分析,选取圆柱坐标系OρΦz为参考系,电流密度与ez同向,相关示意图如图 3所示。
|
图 3 正弦电流流过波导丝等效示意图 |
根据安培环流定律,可以得到
| $ \oint\limits_C {\mathit{\boldsymbol{H'}} \cdot {\rm{d}}\mathit{\boldsymbol{l}}} = H' \cdot 2{\rm{ \mathsf{ π} }}\rho = I。$ | (10) |
波导丝在稳恒电流作用的情况下,其面电流分布是均匀的,于是,面电流密度可表示为
| $ J = \frac{{I'}}{{{\rm{ \mathsf{ π} }}{r^2}}}。$ | (11) |
那么,通过截面积为πρ的电流为
| $ I = J \cdot {\rm{ \mathsf{ π} }}{\rho ^2} = \frac{{I'{\rho ^2}}}{{{r^2}}}。$ | (12) |
于是,式(10)可表示为式(13):
| $ H' \cdot 2{\rm{ \mathsf{ π} }}\rho = \frac{{I'{\rho ^2}}}{{{r^2}}}。$ | (13) |
由此可得到距离轴线为ρ处的磁场强度为
| $ H' = \frac{{I'\rho }}{{{\rm{2 \mathsf{ π} }}{r^2}}}。$ | (14) |
最终直流分量对波导丝的磁场特性为
| $ \mathit{\boldsymbol{H'}} = \frac{{I'\rho }}{{{\rm{2 \mathsf{ π} }}{r^2}}}{\mathit{\boldsymbol{e}}_\mathit{\Phi }}。$ | (15) |
波导丝几何结构如图 4所示,设Fe83Ga17波导丝的电导率为σ,磁导率为μ;分析正弦电流信号对波导丝的作用,可将其看成圆柱体内通有角频率为wn的正弦电流i,如式(16)所示。
| $ i = \sqrt 2 {I_n}\cos {w_n}t。$ | (16) |

|
图 4 环形磁场的H-r-t三维立体图 |
因为波导丝满足轴对称性,所以其电流密度可表示为
| $ \mathit{\boldsymbol{\dot J}} = {{\dot J}_z}\left( \rho \right){{\bf{e}}_z}。$ | (17) |
根据麦克斯韦方程组中法拉第电磁感应定律的微分形式,可得:
| $ \nabla \times E = - \frac{{\partial B}}{{\partial t}}。$ | (18) |
由于磁致伸缩波导丝材料是均匀、线性的简单媒质,因此,其存在如下本构关系:
| $ \mathit{\boldsymbol{J}} = \sigma \mathit{\boldsymbol{E}}。$ | (19) |
| $ \mathit{\boldsymbol{B}} = \mu \mathit{\boldsymbol{H}}。$ | (20) |
将式(19)、(20)代入式(18),由此可得:
| $ \nabla \times \mathit{\boldsymbol{J}} = - \sigma \mu \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial t}}。$ | (21) |
在式(21)两端同时进行旋度运算,根据其不变性可得:
| $ \nabla \times \left( {\nabla \times \mathit{\boldsymbol{J}}} \right) = \nabla \times \left( { - \sigma \mu \frac{{\partial \mathit{\boldsymbol{H}}}}{{\partial t}}} \right)。$ | (22) |
据麦克斯韦方程组中电流定律的微分形式,有
| $ \nabla \times \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{J}}。$ | (23) |
而矢量旋度与散度之间的相互运算关系,有
| $ \nabla \times \left( {\nabla \times \mathit{\boldsymbol{J}}} \right) = \nabla \left( {\nabla \cdot \mathit{\boldsymbol{J}}} \right) - {\nabla ^2}\mathit{\boldsymbol{J}} = - {\nabla ^2}\mathit{\boldsymbol{J}}。$ | (24) |
由此,式(22)可以表达为另一形式
| $ {\nabla ^2}\mathit{\boldsymbol{J}} - \sigma \mu \frac{{\partial \mathit{\boldsymbol{J}}}}{{\partial t}} = 0。$ | (25) |
将式(17)代入式(25),可得相量形式的标量方程
| $ {\nabla ^2}{{\dot J}_z}\left( \rho \right) - j{w_n}\sigma \mu {{\dot J}_z}\left( \rho \right) = 0。$ | (26) |
在圆柱坐标系中,上式表示为
| $ \frac{{{{\rm{d}}^2}{{\dot J}_z}}}{{{\rm{d}}{x^2}}} + \frac{1}{x}\frac{{{\rm{d}}{{\dot J}_z}}}{{{\rm{d}}x}} + {{\dot J}_z} = 0, $ | (27) |
式中:
| $ x = k\rho ,{k^2} = - j{w_n}\sigma \mu 。$ | (28) |
由于在柱坐标系下对拉普拉斯方程进行变量分离,可以得到贝塞尔方程这一特殊的常微分方程,即
| $ {x^2}\frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}} + x\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \left( {{x^2} - {v^2}} \right)y = 0。$ | (29) |
上式可以变形为
| $ \frac{{{{\rm{d}}^2}y}}{{{\rm{d}}{x^2}}} + \frac{1}{x}\frac{{{\rm{d}}y}}{{{\rm{d}}x}} + \left( {1 - \frac{{{v^2}}}{{{x^2}}}} \right)y = 0。$ | (30) |
对比式(27)和式(30)可知,当式(30)在v=0时,其与式(27)具有相同的形式,因此,式(27)的求解可以借助贝塞尔方程的求解过程。
当x→0时,Y0(x)→∞,而式(27)的解是有阶非零的,所以应取B=0,于是,式(27)的有界非零解可表示为
| $ {{\dot J}_z}\left( \rho \right) = A{J_0}\left( {k\rho } \right)。$ | (31) |
根据相量矢量与时域相关量的转换关系,可得通过波导丝的电流
| $ \begin{array}{l} \dot I = \int_{\rm{s}} {\dot J \cdot {\rm{d}}S} = \int_0^{2{\rm{ \mathsf{ π} }}} {{\rm{d}}\mathit{\Phi }} \int_0^r {{{\dot J}_z}\left( \rho \right)\rho {\rm{d}}\rho } = \\ 2{\rm{ \mathsf{ π} }}A\int_0^r {{J_0}\left( {k\rho } \right)\rho {\rm{d}}\rho } = {I_n}。\end{array} $ | (32) |
结合积分公式,0阶和1阶第一类贝塞尔函数的关系式如下[10]:
| $ \int_0^z {{J_0}\left( t \right)t{\rm{d}}t} = z{J_1}\left( z \right)。$ | (33) |
由式(32)和(33),可求得待定系数A为
| $ A = \frac{{k{I_n}}}{{2{\rm{ \mathsf{ π} }}r{J_1}\left( {kr} \right)}}。$ | (34) |
因此,磁致伸缩波导丝内的传导电流密度为
| $ \dot J = \frac{{k{I_n}}}{{2{\rm{ \mathsf{ π} }}r}}\frac{{{J_0}\left( {k\rho } \right)}}{{{J_1}\left( {kr} \right)}}{\mathit{\boldsymbol{e}}_z}。$ | (35) |
从而,导体内的电场为
| $ \dot E = \frac{{\dot J}}{\sigma } = \frac{{k{I_n}}}{{2{\rm{ \mathsf{ π} }}r\sigma }}\frac{{{J_0}\left( {k\rho } \right)}}{{{J_1}\left( {kr} \right)}}{\mathit{\boldsymbol{e}}_z}。$ | (36) |
又因为贝塞尔函数的导数公式具有以下性质
| $ {{J'}_0}\left( z \right) = - {J_1}\left( z \right)。$ | (37) |
从而磁场强度的相量可表示为
| $ {{\mathit{\boldsymbol{\dot H}}}_n} = - \frac{1}{{j{w_n}\mu }}\nabla \times \mathit{\boldsymbol{\dot E}} = \frac{{{I_n}}}{{2{\rm{ \mathsf{ π} }}r}}\frac{{{J_1}\left( {{k_n}\rho } \right)}}{{{J_1}\left( {{k_n}r} \right)}}{\mathit{\boldsymbol{e}}_\mathit{\Phi }}。$ | (38) |
最终,可得正弦分量对波导丝的磁场特性为
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_n} = \sqrt 2 \mathit{Re}\left( {{{\mathit{\dot H}}_n}{{\rm{e}}^{j{w_n}t}}} \right) = \\ \;\;\;\;\;\;\;\;\;\sqrt 2 \mathit{Re}\left( {\frac{{{I_n}}}{{2{\rm{ \mathsf{ π} }}r}}\frac{{{J_1}\left( {{k_n}\rho } \right)}}{{{J_1}\left( {{k_n}r} \right)}}{\mathit{\boldsymbol{e}}^{j{w_n}t}}} \right){\mathit{\boldsymbol{e}}_\mathit{\Phi }}。\end{array} $ | (39) |
利用叠加原理分别将直流分量和正弦分量通过波导丝产生的磁场进行叠加便可求得波导丝的环形磁场H。
| $ \mathit{\boldsymbol{H = }}\left( {\sum\limits_{n = 1}^{10\;000} {{H_n} + H'} } \right){\mathit{\boldsymbol{e}}_\mathit{\Phi }}。$ | (40) |
利用数学软件MATLAB对磁场模型进行分析,不仅能够验证模型的正确性,还能直观反映Fe83Ga17波导丝的磁场特性。在MATLAB设计处理中,为了全面反映磁场特性,笔者采用了基于磁场强度H、时间t以及距离轴线的半径r的三维立体分析方案,最终得到的环形磁场H-r-t三维立体图如图 4所示。
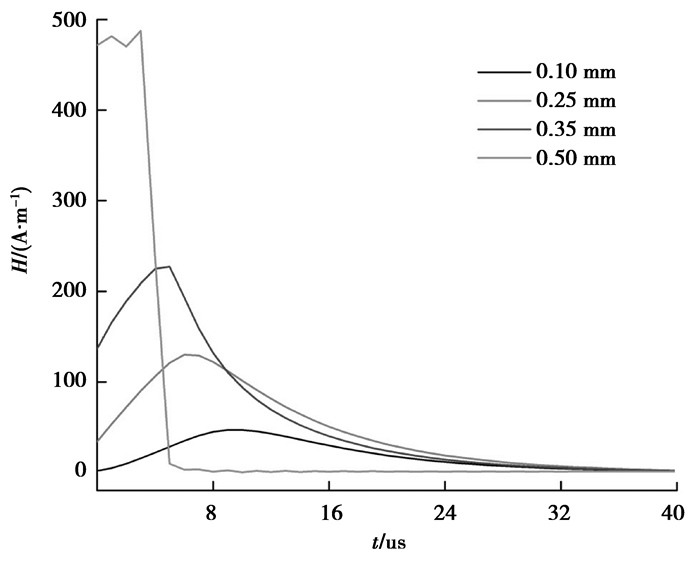
由图可知,磁场强度H与时间t以及距离轴线半径r的关系比较复杂,并不是简单的线性关系,总的来说可以得到两点:一是磁场在波导丝上维系的时间很短;二是磁场强度在波导丝表面处聚集。为了更进一步对磁场的H-t关系进行分析,任意选取波导丝上不同位置的几个参考点,其H-t曲线图如图 5所示。
|
图 5 波导丝不同位置的H-t曲线图(50 μs范围内) |
由图可知,在脉冲周期内激励电流刚作用于波导丝时,波导丝的磁场强度最大,并会因为激励脉宽的缘故维系一定时间,然后随着时间的增加逐步削弱直至消失,整个过程时间很短,在宏观上可以理解为瞬时。此外,波导丝外表面的磁场强度不仅最大,而且消失的最快,这种磁场特性有利于单一弹性波的产生,避免了信号间的干扰。这就为MDS测量的准确性奠定了基础。
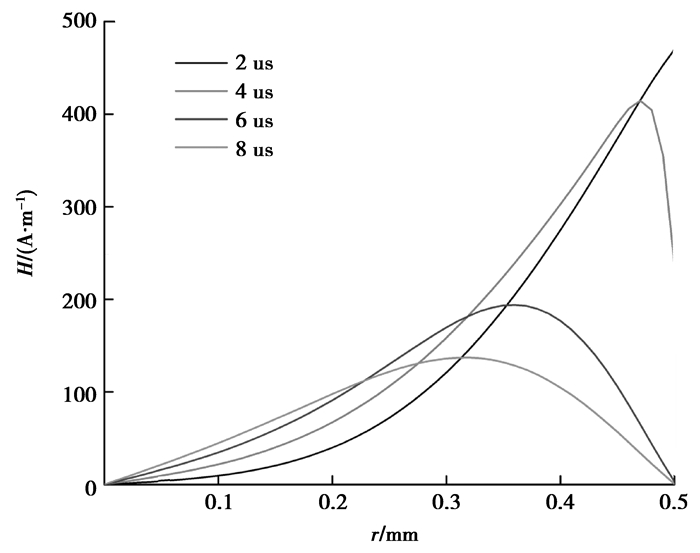
同样,为了更进一步对环形磁场的H-r关系进行分析,任选了几个参考时刻,波导丝的H-r曲线图如图 6所示。
|
图 6 波导丝不同时刻的H-r曲线图 |
由图可知,波导丝上的磁场强度随着离轴线的距离长度的增加而增强,并且增长幅度呈现先小后大的变化趋势,这主要是因为激励电流作用于波导丝产生了趋肤效应的缘故,这使得磁场线在波导丝表面处聚集。根据磁致伸缩位移传感器原理,波导丝表面处因威德曼效应而产生的微小形变是弹性波产生的基础。因此,磁场强度在波导丝表面处最强有利于加强威德曼效应的效果,进而起到增强弹性波,增大MDS量程的作用。此外可以看出,波导丝外表处的磁场强度不仅增加得快而且消失得也快,这有利于磁致伸缩的产生和消失,对后续回波信号的测试大有裨益。
5 信号特性测试信号特性测试是波导丝能否应用于磁致伸缩位移传感器最为关键的一步实验论证,其主要包括电子系统方案和信号测试结果两部分。
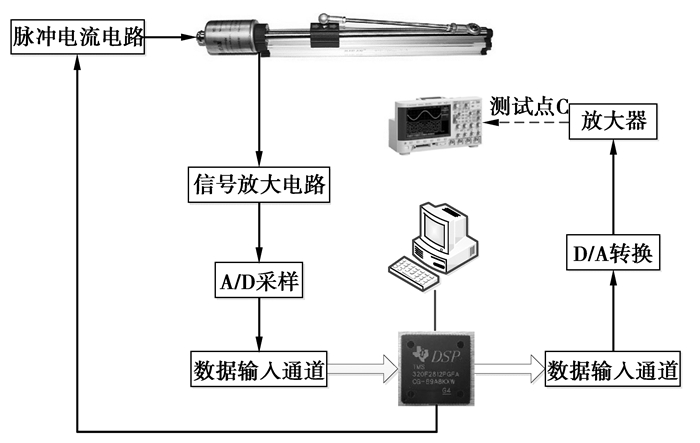
磁致伸缩位移传感器信号测试系统如图 7所示。由图可知,电子系统主要由DSP微处理器,激励电流电路,波导丝单元,信号放大电路,AD采样电路以及通信电路等部分组成。
|
图 7 磁致伸缩位移传感器信号测试框图 |
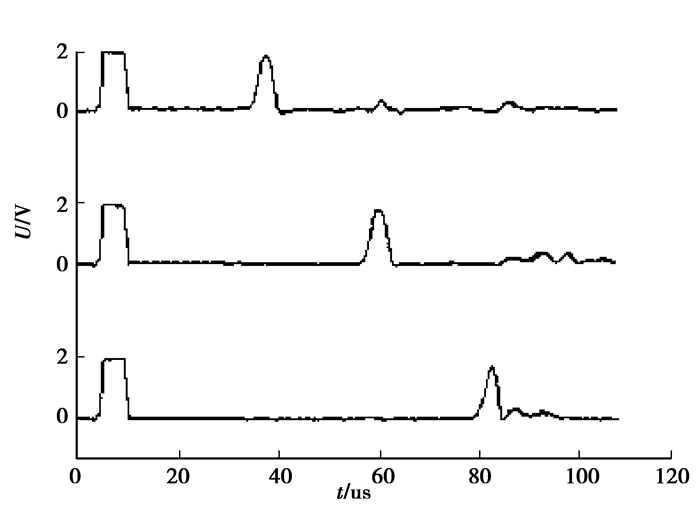
测试长5 m的波导丝前、中、末端时,示波器得到的回波信号如图 8所示。由图可知,MDS采用Fe83Ga17波导丝后,不仅回波信号效果很好,而且波导丝对回波信号长距离传输过程中造成的衰减也很小。这不仅说明了Fe83Ga17波导丝具有良好的电磁特性,而且从电子学的角度对Clark的磁致伸缩特性研究[6]和李纪恒的威德曼效应研究[7]进行了论证。
|
图 8 回波信号 |
针对国产MDS因Fe-Ni波导丝饱和磁致伸缩系数过小而导致的量程过短的问题,在Clark研究的基础上,提出了将Fe83Ga17波导丝应用于MDS的新方案,并从傅里叶分析和电磁学理论的角度建立了Fe83Ga17波导丝新的磁场模型。MATLAB对磁场模型的分析表明,Fe83Ga17波导丝的电磁特性有利于增强MDS的威德曼效应,这就为新方案提供了理论基础;测试系统对信号特性的测试结果表明,基于Fe83Ga17波导丝的MDS具有回波信号强,长距离传输衰减小的特征,从而有助于增加MDS的量程,这在电子学上证明了方案的可行性。
| [1] |
刘俊, 秦岚, 刘京诚, 等.
平板式压电四维力/力矩传感器的研究与开发[J]. 重庆大学学报, 2011, 34(2): 101–107.
LIU Jun, QIN Lan, LIU Jingcheng, et al. Research and development of a parallel piezoelectric 4-axis force/torque sensor[J]. Journal of Chongqing University, 2011, 34(2): 101–107. (in Chinese) |
| [2] |
何永琦, 陈伟民, 符欲梅.
倾斜传感器在桥梁变形监测中的应用[J]. 重庆大学学报:自然科学版, 2004, 27(7): 28–31.
HE Yongqi, CHEN Weimin, FU Yumei. Bridge deformation monitoring with tiltmeter[J]. Journal of Chongqing University:Natural Science Edition, 2004, 27(7): 28–31. (in Chinese) |
| [3] | Calkins F T, Flatau A B, Dapino M J. Overview of magnetostrictive sensor technology[J]. Journal of Intelligent Material Systems and Structures, 2007, 18(10): 1057–1066. DOI:10.1177/1045389X06072358 |
| [4] |
卢云, 申蓉, 冯哲圣, 等.
Ni-Fe合金磁致伸缩波导丝特性研究[J]. 功能材料, 2009, 40(11): 1791–1793.
LU YUN, SHEN RONG, FENG Zhesheng, et al. Research on properties of magnetostriction NiFe alloy for displacement sensor[J]. Journal of Functional Materials, 2009, 40(11): 1791–1793. DOI:10.3321/j.issn:1001-9731.2009.11.008 (in Chinese) |
| [5] |
李晓诚, 丁雨田, 胡勇.
Tb0.3Dy0.7Fe1.95-xTix(x=0, 0.03, 0.06, 0.09)合金的微观组织与磁致伸缩性能[J]. 金属学报, 2012, 48(1): 11–15.
LI Xiaocheng, DING Yutian, HU Yong. Microstructure and magnetostriction of the Tb0.3Dy0.7Fe1.95-xTix(x=0, 0.03, 0.06, 0.09[J]. Acta Metallurgica Sinica, 2012, 48(1): 11–15. (in Chinese) |
| [6] | Clark A E, Restorff J B, Wun-Fogle M, et al. Magnetostrictive properties of body-centered cubic Fe-Ga and Fe-Ga-Al alloys[J]. IEEE Transactions on Magnetics, 2000, 36(5): 3238–3240. DOI:10.1109/20.908752 |
| [7] | Li J H, Gao X X, Zhu J, et al. Wiedemann effect of Fe-Ga based magnetostrictive wires[J]. Chinese Physics B, 2012, 21(8): 476–481. |
| [8] |
余超, 周新志, 熊胤琪.
Fe83Ga17磁致伸缩位移传感器激励信号的ANSYS分析及DSP实现[J]. 仪表技术与传感器, 2012(8): 4–6, 80.
YU Chao, ZHOU Xinzhi, XIONG Yinqi. Research on excitation signal of Fe83Ga17 magnetostrictive displacement sensor based on ANSYS and DSP[J]. Instrument Technique and Sensor, 2012(8): 4–6, 80. (in Chinese) |
| [9] | Zhou X Z, Yu C, Xiong Y Q, et al. Research on Fe(100-x)Gax alloy applied to magnetostrictive displacement sensors[J]. Applied Mechanics and Materials, 2012, 226/227/228: 2154–2159. |
| [10] | Abramowitz M, Stegun I A. Handbook of mathematical functions:with formulas, graphs, and mathematical tables[M].[S.l.]:Courier Dover Publications, 1964. |
| [11] | Seco F, Martin J M, Jimenez A R. Improving the accuracy of magnetostrictive linear position sensors[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(3): 722–729. DOI:10.1109/TIM.2008.2005260 |
| [12] | Ktena A, Manasis C, Papadopoulos C, et al. Measurement system for a magnetostrictive torque sensor[C]//Proceedings of the 200916th International Conference on Systems, Signals and Image Processing, June 18-20, 2009, Chalkida, Greece. Piscataway:IEEE Press, 2009:1-4. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5367725 |
| [13] | Ruderman M. , Bertram T[J]. IEEE Transactions on Magnetics, 2012, 48(4): 1281–1284. DOI:10.1109/TMAG.2011.2172931 |
| [14] | Li W, Kim I H, Jang S M, et al. Hysteresis modeling for electrical steel sheets using improved vector Jiles-Atherton hysteresis model[J]. IEEE Transactions on Magnetics, 2011, 47(10): 3821–3824. DOI:10.1109/TMAG.2011.2158296 |
 2013, Vol. 36
2013, Vol. 36

