2. 加拿大皇后大学 电子与计算机工程系, 加拿大安大略省金斯顿市 K7L3N6
2. Faculty of Engineering and Applied Science, Queen's University, Kingston K7 L3 N6, Canada
正激变换器是一种电路结构简单的隔离型DC-DC功率变换器,被广泛地应用于需要电气隔离的中小功率场合[1-4]。为了克服正激变换器的磁复位问题,已提出有源钳位、双管正激、谐振磁复位等拓扑结构形式的正激变换器。其中,双管正激变换器(DTFC)[5-6]无需变压器磁芯复位电路,有着开关管应力低、能够有效地避免桥臂直通等优点,因此获得了广泛地关注和研究。为了提高双管正激变换器的转换效率和功率等级,文献[7]研究了DTFC的软开关技术,使之适用于宽范围输入、高效率要求的应用场合。文献[8]利用饱和电感实现了有源钳位双管正激变换器的零电压开关技术。文献[9]应用峰值电流控制算法调节交错串-并联双管正激变换器的两主开关管,实现输入端功率的均衡和均压。
目前,提高双管正激变换器的效率、降低开关损耗等问题已得到深入探讨,然而在改善双管正激变换器的动态性能,减少恢复时间等方面却少有研究。事实上,随着DC-DC功率变换器在供电电源中的应用越来越广泛,对其在大扰动信号下的动态响应要求也越来越高。这一问题现已引起了国内外学者的注意:文献[10]将模糊逻辑控制理论应用于Boost变换器中;文献[11]提出了采用滑模控制方法提高QSPRC变换器的动态性能,这些方法在一定程度上提高了变换器的动态性能,但都不能使变换器的动态性能达到最优;文献[12]研究了一种数字预测方案运于提高Buck变换器的动态性能,但数学推导过程较为繁琐;文献[13-14]基于电容充放电平衡(capacitor balance control,CBC)控制算法,设计了一类控制器用于优化Buck变换器的动态响应,但没有考虑到占空比信号受限时的情况,因此不能应用于隔离型的功率变换器。
笔者在分析DTFC动态过程和电容充放电平衡控制原理的基础上,考虑当占空比信号受限制时,功率变换器动态性能的最优控制问题,采用一种近似计算的方法,扩展了CBC控制算法的应用范围,推导出开关器件的最佳切换时间和最优占空比信号。最后通过仿真和实验验证了该算法的有效性。
1 电容电荷平衡控制策略电容电荷平衡是指在瞬态过程中双管正激变换器的输出电容的充电电荷量和放电电荷量相等[13]。即
| $ {v_{\rm{C}}}\left( {{t_1}} \right)-{v_{\rm{C}}}\left( {{t_0}} \right) = \frac{{{I_{{\rm{Cavg}}}}}}{C} = 0, $ | (1) |
| $ \frac{{\int_{{t_0}}^{{t_1}} {{i_{\rm{C}}}\left( t \right){\rm{d}}t} }}{{{t_1}-{t_0}}} = 0, $ | (2) |
其中:vC(t),iC(t)为输出电容的电压和电流;t0和t1为瞬态过程的起始时刻和结束时刻。若式(2)成立,则表明瞬态过程结束后,输出电容的充电电荷和放电电荷相等,双管正激变换器的输出电压回到了参考电压,这也就意味着功率变换器达到新的稳态。
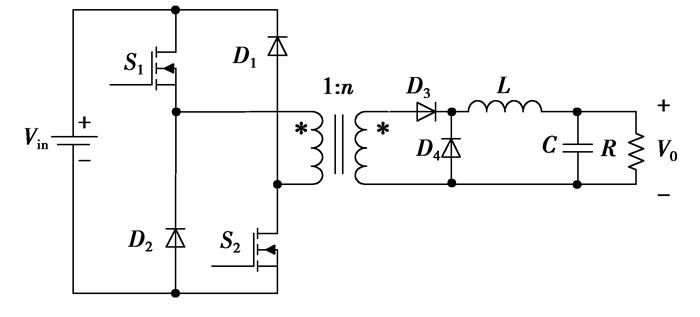
|
图 1 双管正激变换器 |
下面以双管正激变换器负载电流发生正跃变时的最优动态响应过程为例,介绍CBC控制算法的基本原理。
如图 2所示,负载电流在P0点处发生正跃变,由于电感电流iL不能突变,输出电容开始放电以维持新的负载电流值io2,导致DTFC的输出电压逐渐下降,偏离参考电压值Vref。为了使得电感电流iL以最快速度上升,控制DTFC以最大占空比(50%)开通。在P1点时,电感电流iL与新的负载电流相等,电容放电过程结束,此时输出电压达到最低点。随着电感电流的继续增加,输出电容开始充电,变换器的输出电压逐渐回升。在P2点,电感电流达到峰值,然后开始下降。为了保证充电过程能在最短时间内结束,在T2时间段内控制占空比信号始终为0。在P3点,输出电容的充电电荷等于放电电荷,电感电流与形面积转变为易于计算的三角形输出电压同时回到稳态,DTFC的最优动态响应过程结束。
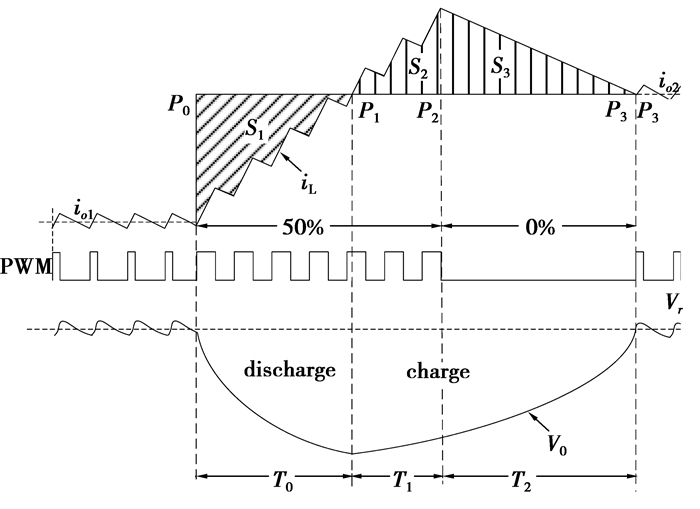
|
图 2 负载正跃变时双管正激变换器的最优动态响应曲线 |
综上所述,CBC控制算法的关键在于根据电容充放电平衡原理准确地计算出电感电流iL到达峰值的时刻,即图 2中的P2点。
2 理论分析考虑到电感电流iL、负载电流io和电容电流iC三者之间存在如下关系式:
| $ {i_{\rm{o}}} = {i_{\rm{L}}} + {i_{\rm{C}}}。$ | (3) |
因此,CBC控制算法中的输出电容充放电平衡原理等价于图 2中电感电流和输出电流之间的放电面积与充电面积相等,即
| $ {S_1} = {S_2} + {S_3}。$ | (4) |
但是由于变压器的磁芯复位问题,DTFC的最大占空比被限制为50%,从而导致面积S1和S2为不规则形状的区域,难以直接计算。因此这里考虑一种近似计算的方法,利用两个对角三角形面积对消的原则,将不规则的图形面积转变为易于计算的三角形面积,如图 3所示。
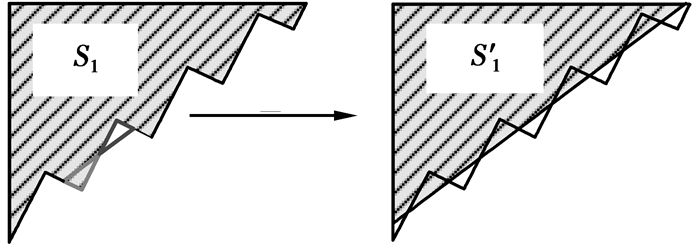
|
图 3 近似计算方法示意图 |
按照上述近似计算的方法,图 2中输出电容的充电面积和放电面积变换成如图 4所示。
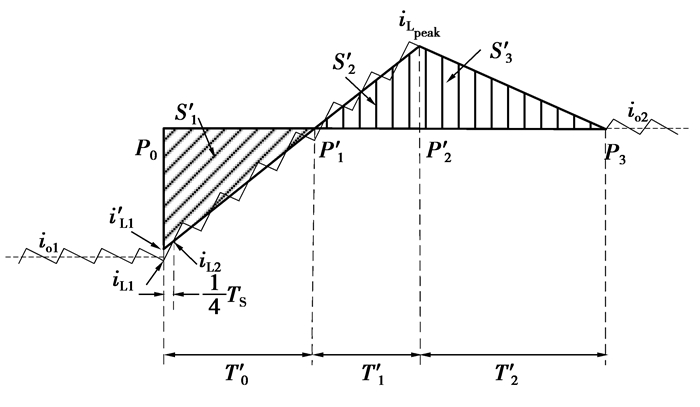
|
图 4 近似计算后的输出电容放电/充电面积示意图 |
因此,笔者所提出的CBC控制算法的具体实现如下:
1) 当检测到输出电压的波动超过给定值,则从电压模式控制切换到CBC控制模式。
2) 估算新的负载电流io2。在跳变点以及延迟Ts/4后检测电感电流和输出电压值,并根据输出电容的电流电压关系式:
| $ {i_{\rm{C}}}{\rm{ = }}C\frac{{{\rm{d}}{v_{\rm{C}}}}}{{{\rm{d}}t}}, $ | (5) |
可得:
| $ \begin{array}{l} {i_{\rm{C}}} = C\Delta {v_{\rm{C}}}\frac{4}{{{T_S}}} \Rightarrow {i_{{\rm{o}}2}}-\frac{1}{2}\left( {{i_{{L_1}}}-{i_{{L_2}}}} \right){\rm{ = }}\\ \;\;\;\;\;\;C\left( {{v_{{{\rm{o}}_{\rm{1}}}}}-{v_{{{\rm{o}}_{\rm{2}}}}}} \right)\frac{4}{{{T_{\rm{S}}}}}\\ \;\;\; \Rightarrow {i_{{\rm{o}}2}} = \frac{1}{2}\left( {{i_{{L_1}}} + {i_{{L_2}}}} \right) + \;C\left( {{v_{{{\rm{o}}_{\rm{1}}}}} - {v_{{{\rm{o}}_{\rm{2}}}}}} \right)\frac{4}{{{T_{\rm{S}}}}}。\end{array} $ | (6) |
3) 计算电容放电面积。重新计算电感电流上升斜率和下降的斜率。
| $ \frac{{d{{i'}_{\rm{L}}}}}{{{\rm{d}}t}}\left| {_{{\rm{rising}}}} \right. = \frac{{n{v_{{\rm{in}}}}-2{v_{\rm{o}}}}}{{2L}} = {k_1}, $ | (7) |
| $ \frac{{d{{i'}_{\rm{L}}}}}{{{\rm{d}}t}}\left| {_{{\rm{falling}}}} \right. =- \frac{{{v_{\rm{o}}}}}{L} = {k_2}, $ | (8) |
其中:vin、vo为输入电压和输出电压;n为变压器副边与原边的匝数比。则根据面积计算公式得输出电容放电面积S′1。
| $ {{T'}_0} = \frac{{{i_{{{\rm{o}}_{\rm{2}}}}}-{{i'}_{{{\rm{L}}_{\rm{1}}}}}}}{{{k_1}}}, {{S'}_1} = \frac{1}{2}{{T'}_0}\left( {{i_{{\rm{o2}}}}-{{i'}_{{{\rm{L}}_{\rm{1}}}}}} \right). $ | (9) |
其中,i′L1为P0点检测的电感电流经过近似计算后的值,计算公式为
| $ {{i'}_{{{\rm{L}}_{\rm{1}}}}} = {{i'}_{{{\rm{L}}_{\rm{1}}}}} + \frac{{n{v_{{\rm{in}}}}}}{L}\frac{{{T_{\rm{s}}}}}{8}。$ | (10) |
4) 计算电容的充电面积。根据图 4可得,输出电容的充电面积为
| $ {{S'}_2} = \frac{1}{2}{{T'}_1}\left( {{i_{{{\rm{L}}_{{\rm{peak}}}}}}-{i_{{\rm{o2}}}}} \right);{{S'}_3} = \frac{1}{2}{{T'}_2}\left( {{i_{{{\rm{L}}_{{\rm{peak}}}}}}-{i_{{\rm{o2}}}}} \right)。$ | (11) |
其中P′2点的电感电流峰值iLpeak又可计算为
| $ {i_{{{\rm{L}}_{{\rm{peak}}}}}} = {i_{{\rm{o2}}}} + {k_1}{{T'}_1} = {i_{{\rm{o2}}}} + {k_2}{{T'}_2}。$ | (12) |
5) 根据电容充放电平衡原理计算时间段T′1和T′2。根据电容放电面积和充电面积相等的原则:
| $ {S'_1} = {S'_2} + {S'_3}, $ | (13) |
并代入式(9)、(11)和(12),则有:
| $ {T'_1} = \sqrt {\frac{{{{S'}_1}}}{K}}, K = \frac{{{k_1}\left( {{k_1} + {k_2}} \right)}}{{2{k_2}}}, {T'_1} = \frac{{{k_1}}}{{{k_2}}}{T'_2}。$ | (14) |
6) 计算时间段T0、T1和T2。采用近似计算的方式后,图 2中的P1和P2点对应图 4中P′1和P′2,有:
| $ {T_0} \approx {T'_0}, {T_1} = {T'_1}-\frac{{{T_{\rm{S}}}}}{4}, {T_2} = {T'_2} + \frac{{{T_{\rm{S}}}}}{4}。$ | (15) |
7) 根据计算出的最佳切换时间。在T0+T1时间段内输出50%的占空比信号,然后关断开关管,在经过时间段T2之后,从CBC控制模式再切换回电压模式,进入下一个稳态。
3 仿真验证和实验为了验证所提出的算法的可行性和有效性,设计了一台额定功率为100 W的双管正激变换器测试样机。具体参数如下:输入电压Vin=48 V,输出电压V0=12 V,L=15 uH,C=100 uF,开关频率fs=250 kHz,变压器匝数比n=5:6。图 5、6分别给出了控制原理框图和实验样机图。
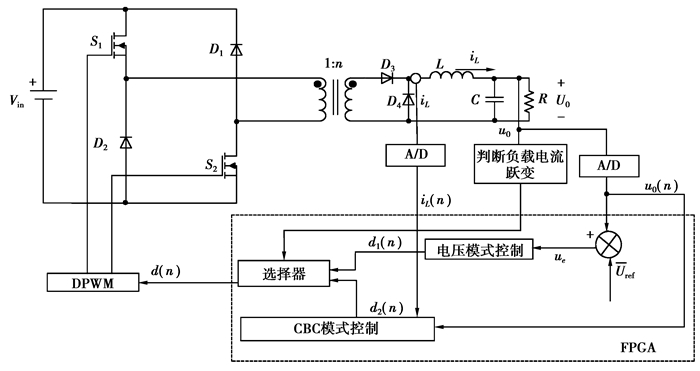
|
图 5 控制原理框图 |

|
图 6 样机实物图 |
利用Matlab实现负载电流发生正跃变情况下的仿真研究,假设负载电流从3 A跳变至6 A,仿真结果如图 7所示。
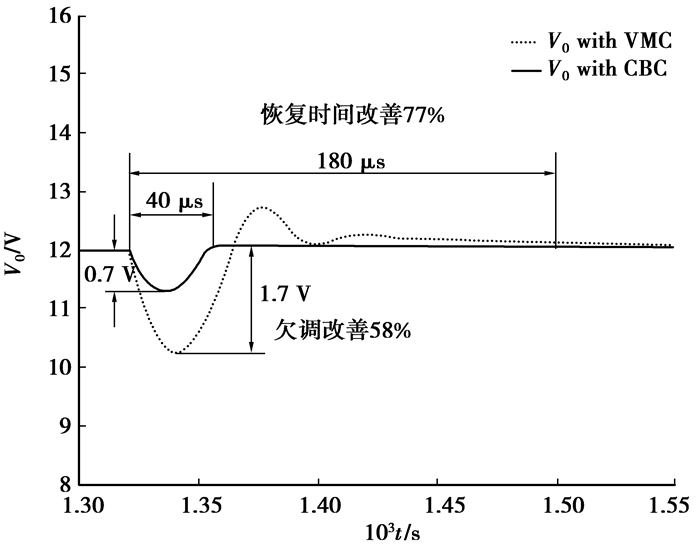
|
图 7 负载电流正跃变仿真结果(3 A→6 A) |
从图 7可以看出,运用笔者所提出的CBC控制算法,DTFC的输出电压欠调量为0.7 V,调节时间为40 μs。而传统电压模式控制的输出电压欠调量为1.7 V,调节时间为180 μs。相比之下,运用电容电荷平衡控制方法后,DTFC的输出电压欠调量减少了58%,调节时间缩短了77%。显然,DTFC的动态性能有了显著的改善。
3.2 实验结果采用Altera公司DE2-70 FPGA开发板验证笔者提出的控制算法,通过倍频的方式产生100 MHz的时钟信号实时检测DTFC的输出电压值,并经过数字滤波后与设定的阀值比较,判断负载是否发生突变,由FPGA的控制芯片执行相应的控制算法。DPWM信号采用计数器和延迟线混合的方法予以实现[15]。
图 8、9分别为DTFC在电压模式控制算法和CBC控制算法下的实验波形图。两图中输出电压测量均为交流模式,方便观测波形。从图上看,CBC控制算法的输出电压欠调量比电压模式控制算法减少了39%,调节时间比电压模式控制算法缩短了84%。因此,采用笔者所提电容电荷平衡控制方案可以明显改善DTFC的动态性能,大大降低了负载扰动时的超调量和调整时间。
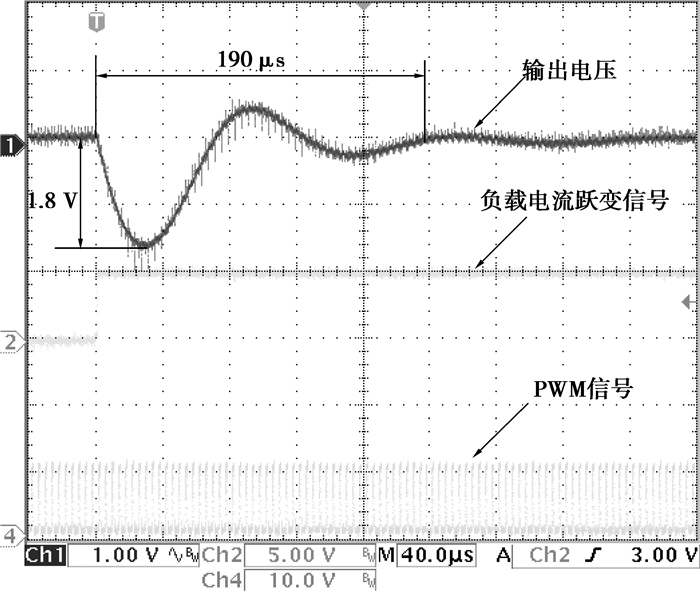
|
图 8 DTFC电压模式控制算法的实验波形(3 A→6 A) |
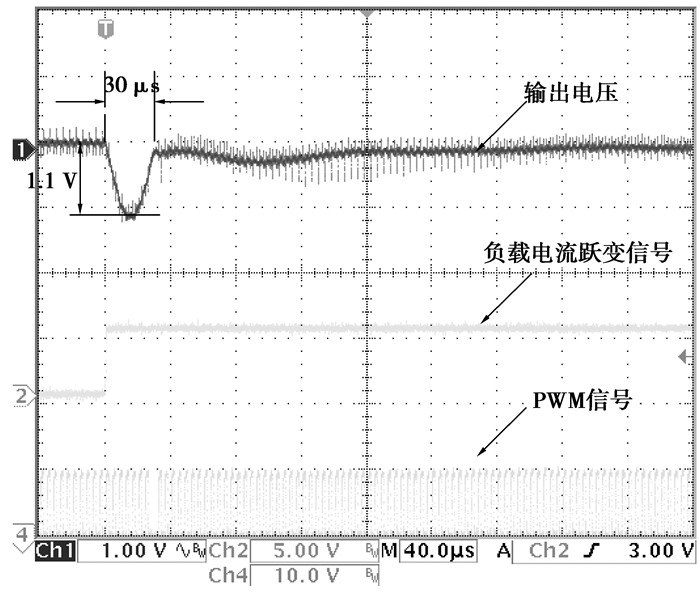
|
图 9 DTFC电容充放电平衡控制算法的实验波形(3 A→6 A) |
笔者针对双管正激变换器的动态性能问题,利用近似计算方法,提出了一种基于电荷平衡原理的控制方案,得出如下结论:
1) 采用输出电容在瞬态过程中电荷平衡的控制策略,可以大大提高DTFC在负载扰动时的动态响应性能;
2) 采用近似计算的方法,将复杂的计算过程予以简化,降低了CBC控制算法的计算量,有利于控制器的设计和实现;
3) 尽管笔者所提方案是针对双管正激变换器展开的,但所采用的方法对其他占空比信号受限的DC-DC功率变换器也同样具有参考价值。
| [1] | Abramovitz A, Tang C, Smedley K. Analysis and design of forward converter with energy regenerative snubber[J]. IEEE Transactions on Power Electronics, 2010, 25(3): 667–676. DOI:10.1109/TPEL.2009.2033275 |
| [2] | Lin B R, Chen C C, Wan J F, et al. Soft switching interleaved forward converter with current doubler rectifier[C]//Proceedings of the 20072nd IEEE Conference on Industrial Electronics and Applications, May 23-25, 2007, Harbin, China. Piscataway:IEEE Press, 2007:1244-1249. http://www.researchgate.net/publication/251841051_Soft_Switching_Interleaved_Forward_Converter_with_Current_Doubler_Rectifier |
| [3] | Park K B, Kim C E, Moon G W, et al. Three-switch active-clamp forward converter with low switch voltage stress and wide ZVS range for high-input-voltage applications[J]. IEEE Transactions on Power Electronics, 2010, 25(4): 889–898. DOI:10.1109/TPEL.2009.2036620 |
| [4] | Wang D, He X N, Shi J J. Design and analysis of an interleaved flyback-forward boost converter with the current autobalance characteristic[J]. IEEE Transactions on Power Electronics, 2010, 25(2): 489–498. DOI:10.1109/TPEL.2009.2025762 |
| [5] | Gu X M, Gu Y L, Huang L J, et al. A novel ZVS resonant reset dual wwitch forward DC/DC converter[C]//Proceedings of the 2004 IEEE 35th Annual Power Electronics Specialists Conference, June 20-25, 2004, Aachen, Germany. Piscataway:IEEE Press, 2004, 4:2708-2712. |
| [6] | Lin B R, Huang C L, Li M Y. Novel zero voltage switching dual-switch forward converter with ripple current cancellation[J]. IET Electric Power Applications, 2007, 1(5): 799–807. DOI:10.1049/iet-epa:20060434 |
| [7] |
洪小圆, 陈威, 吕征宇.
软开关谐振复位双管正激DC/DC变流器[J]. 电工技术学报, 2009, 24(10): 65–70.
HONG Xiaoyuan, CHEN Wei, Lü Zhengyu. Soft-switching resonant reset dual switch forward DC/DC converter[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 65–70. DOI:10.3321/j.issn:1000-6753.2009.10.011 (in Chinese) |
| [8] |
顾晓明, 顾亦磊, 吴燮华.
一种零电压开关有源箝位双管正激变换器[J]. 浙江大学学报:工学版, 2005, 39(9): 1296–1300.
GU Xiaoming, GU Yilei, WU Xiehua. Dual switch forward converter with zero voltage switch active clamp[J]. Journal of Zhejiang University:Engineering Science, 2005, 39(9): 1296–1300. (in Chinese) |
| [9] |
裘迅, 杨双景, 方宇, 等.
交错串联-并联双管正激变换器的一种均压方法[J]. 中国电机工程学报, 2008, 28(24): 1–6.
QIU Xun, YANG Shuangjing, FANG Yu, et al. Voltage sharing control for interleaved series-parallel dual two-transistor forward converters[J]. Proceedings of the CSEE, 2008, 28(24): 1–6. DOI:10.3321/j.issn:0258-8013.2008.24.001 (in Chinese) |
| [10] | Feng G, Zhang W, Liu Y F. A new current mode fuzzy logic controller with extended state observer for DC-to-DC converters[C]//Proceedings of the 19th Annual IEEE Applied Power Electronics Conference, February 22-26, 2004, Anaheim, CA. Piscataway:IEEE Press, 2004, 3:1771-1777. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1296106 |
| [11] | Castilla M, Garcia D V L, Lopez M, et al. Dynamic response optimization of quantum series-parallel resonant converters using sliding mode control[C]//Proceedings of the 2000 IEEE 31st Annual Power Electronics Specialists Conference, June 18-23, 2000, Galway, Ireland. Piscataway:IEEE Press, 2000, 2:702-707. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=879902 |
| [12] | Effler S, Kelly A, Halton M, et al. Digital control law using a novel load current estimator principle for improved transient response[C]//Proceedings of the 2008 IEEE Power Electronics Specialists Conference, June 15-19, 2008, Rhodes, Greek. Piscataway:IEEE Press, 2008:4585-4589. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4592688 |
| [13] | Guang F, Meyer E, Liu Y F. A new digital control algorithm to achieve optimal dynamic performance in DC-to-DC converters[J]. IEEE Transactions on Power Electronics, 2007, 22(4): 1489–1498. DOI:10.1109/TPEL.2007.900605 |
| [14] | Meyer E, Zhang Z L, Liu Y F. An optimal control method for buck converters using a practical capacitor charge balance technique[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1802–1812. DOI:10.1109/TPEL.2008.925201 |
| [15] | Lukic Z, Blake C, Huerta S C, et al. Universal and fault-tolerant multiphase digital PWM controller IC for high-frequency DC-DC converters[C]//Proceedings of the 2007 Twenty Second Annual IEEE Applied Power Electronics Conference, February 25-March 1, 2007, Anaheim, CA, USA. Piscataway:IEEE Press, 2007:42-47. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4195698 |
 2013, Vol. 36
2013, Vol. 36

