2. 邢台职业技术学院 电气工程系, 刑台 054035
2. Department of Electrical, Xingtai Polytechnic College, Xingtai, Hebei 054035, China
在医学超声成像领域,基于声场叠加或图像叠加的合成孔径聚焦(synthetic aperture focusing,SAF)方法得到了广泛应用。与传统的延时叠加波束合成方法相比,合成孔径聚焦成像能够明显提高图像的分辨率,是一种较有潜力的超声成像方法,但是该方法要求采样和存储每一个孔径点的整个回波信号,即全波采样,其重建理论较复杂,且成像的分辨率对于成像深度有很大的依赖性,无论对软件和硬件要求都比较高[1];其次,单一利用合成孔径聚焦技术,超声成像的回波信号信噪比SNR很低,具有较高的旁瓣等级,图像的对比度较差。因此,为进一步提高超声图像的分辨率和增加探测深度,研究学者开展了一系列新方法、新技术的研究。
近年来,虚拟阵元的概念已广泛应用于军事、民用通信及雷达天线探测系统等阵列信号处理领域,基本思想是在保持真实阵元数目不变的情况下,应用虚拟阵元技术使得阵元数目在虚拟上得到增加,从而减小波束宽度,提高分辨率[2]。然而,目前在国内超声成像领域,虚拟阵元技术的相关报道甚少。
随着临床诊断需求的不断增加,对超声成像系统的成像质量提出了更高的要求。笔者将虚拟阵元技术引入到超声成像系统,结合延时叠加(delay-and-sum,DAS)波束合成方法,利用2次延时叠加实现双聚焦波束合成(dual focusing beamforming,DFB)超声成像。该方法通过引入虚拟阵元的概念,结合合成孔径[3-4]聚焦技术,利用两个波束合成器BF1和BF2以及一个FIFO缓存器通过两次延时叠加,无需再存储大量的低分辨率回波数据,就能解决分辨率与探测深度之间的矛盾,进一步提高超声成像的分辨率,同时不降低成像的深度。为了验证该方法的有效性,进行了静态点散射目标的成像实验。
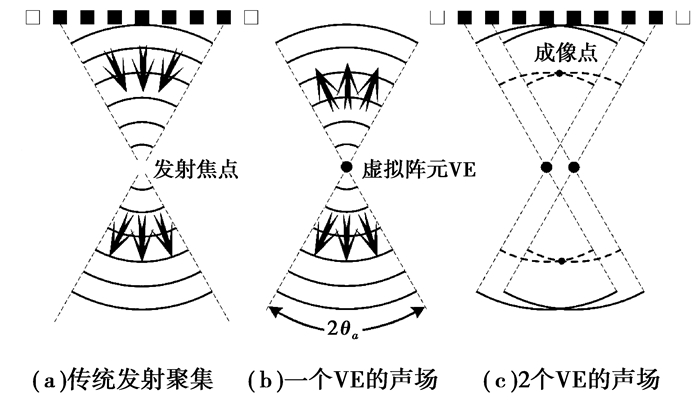
1 基于虚拟阵元的双聚焦波束合成方法在超声成像的发射聚焦过程中,如果信源(signal source)是一个真实的传感器阵元,那么此信源即为实源(real source),否则为虚拟源(virtual source,VS)[5]。Frazier等[6]首先研究了合成孔径技术中VS的应用。不同于天线等阵列信号处理领域的虚拟阵元概念,在超声成像发射聚焦过程中,将发射聚焦点视为一个虚拟源VS[5-6],分别向前后发射声波信号,在接收聚焦过程中,若接收焦点与VS重合,此时虚拟源VS即为一个虚拟阵元(virtual element,VE)。由于合成孔径聚焦及延时叠加波束合成适用于目前现有的任意传感器阵列,如线阵、凸阵以及凹阵探头,笔者仅以线性传感器阵列为例来论证所提出方法的有效性和普遍适用性。图 1(a)即为传统的发射聚焦声场,若发射接收焦点为单一固定的,则焦点即为一个虚拟阵元,如图 1(b)所示,分别向前后发射孔径角为2θa球面波前的声波信号[7]。当存在2个及以上虚拟阵元时,虚拟阵元的声场将出现叠加,如图 1(c)所示。
|
图 1 传统聚焦发射声场与虚拟阵元声场对比图 |
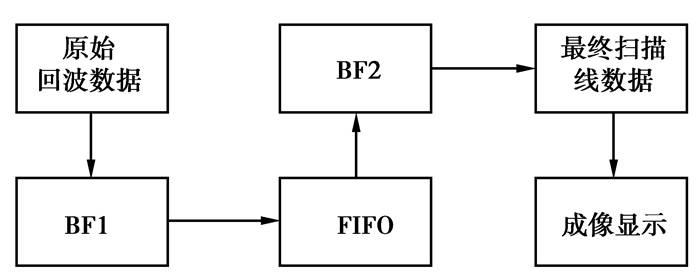
基于虚拟源阵元的双聚焦波束合成原理图如图 2所示。DFB包含2个波束合成器BF1和BF2,以及一个存储BF1输出数据的FIFO缓存器。DFB分2个部分:第1部分利用滑动子孔径,采用固定单一焦点进行发射和接收聚焦,将各个通道的回波数据通过波束形成器BF1进行DAS波束合成,将BF1的输出数据存储在FIFO中;第2部分将FIFO中的数据作为BF2的输入,结合动态聚焦技术,再次进行DAS波束合成,得到最终成像的回波数据。
|
图 2 DFB原理框图 |
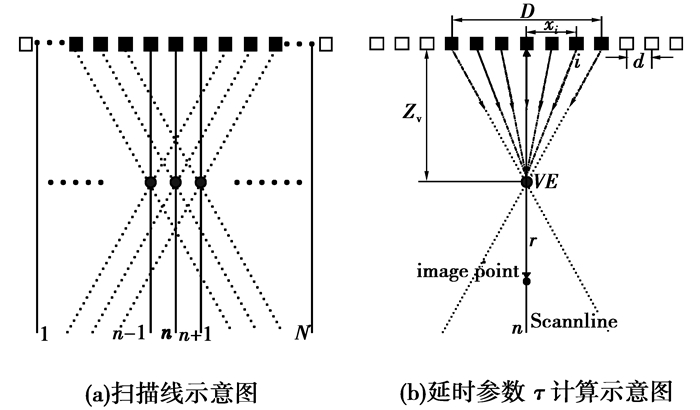
根据上述DFB原理,第一阶段波束合成采用滑动子孔径、单一固定焦点发射接收聚焦模式,利用BF1得到N(其中N为滑动子孔径个数)条扫描线数据,并且声场发生重叠,如图 3(a)所示,图 3(b)给出了形成第n条扫描线时延时参数的计算示意图。
|
图 3 BF1形成扫描线及延时参数计算示意图 |
图 3(b)中,设阵元间距为d,虚拟阵元深度为Zv,聚焦系数为F#,子孔径线性传感器个数[5]L=Zv/F#/d,子孔径大小D=L×d,将子孔径中心定为参照原点,则子孔径中第i个阵元的位置xi为
| $ {x_i} = \left( {i - \frac{{L + 1}}{2}} \right) \times d, i = 1, 2, \cdots, L。$ | (1) |
在VE处聚焦,声速c为已知常数,以子孔径中心作为延迟时间参考点,则阵元i的延时τi:
| $ {\tau _i} = \frac{{\sqrt {{x_i}^2 + {Z_{\rm{v}}}^2} - {Z_{\rm{v}}}}}{c}。$ | (2) |
则该扫描线数据为
| $ {S_n}\left( t \right) = \sum\limits_{i = 1}^L {\omega \left( i \right) \times {s_i}\left( {t - \frac{r}{c} - {\tau _i}} \right)}, $ | (3) |
其中:ω(i)为幅度变迹系数;si(t)为子孔径中阵元i接收到的回波信号;r/c为声波从像点到子孔径中心的传播时间;τi为第i个阵元施加的延时。利用滑动子孔径的概念,经过第一阶段的波束合成,可以得到N条扫描线数据Sn(t)。
1.2 BF2的延时参数计算由图 1(c)可知,多个虚拟阵元的存在会出现声场叠加现象,即同一个采样点包含多个像点的信息。考虑任意样本点ii是否位于编号为jj的虚拟阵元声场内[8-9],可参照式(4)。
| $ {K_{jj, ii}} = \left\{ {\begin{array}{*{20}{c}} {1, }&{{\rm{if}}\left| {\frac{{d\_x}}{{d\_z}}} \right| \le \tan {\theta _{\rm{a}}}, }\\ {0, }&{{\rm{if}}\left| {\frac{{d\_x}}{{d\_z}}} \right| > \tan {\theta _{\rm{a}}};} \end{array}} \right. $ | (4) |
式中:d_x为样本点到相应虚拟阵元的侧向距离;d_z为轴向距离。若Kjj,ii=1,则样本点位于该虚拟阵元的声场内,该样本点即为有效样本点。
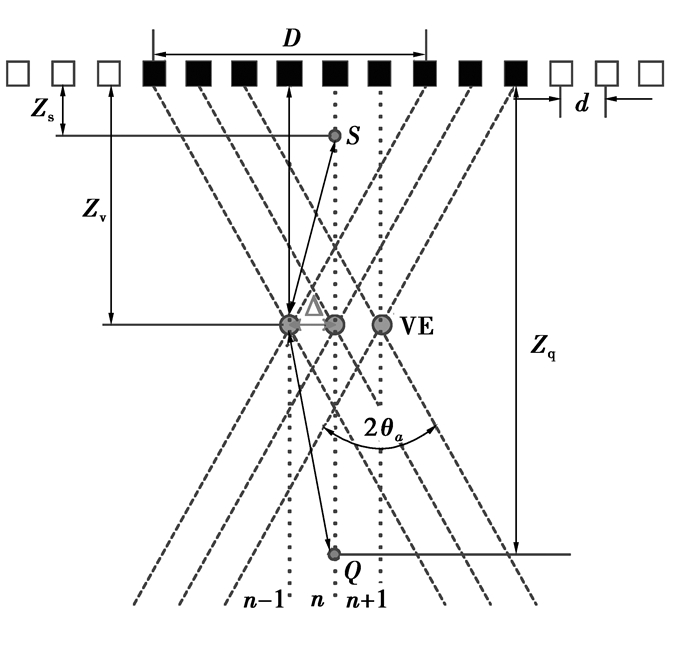
图 4中,D=L×d为滑动子孔径的大小,Zv为虚拟阵元的深度,Zq、Zs分别为样本点Q、S的深度,真实阵元间距d以及虚拟阵元间距Δ,聚焦系数F#=Zv/D,由几何关系可得半孔径角θa:
| $ {\theta _{\rm{a}}} = \arctan \frac{D}{{2 \times {Z_{\rm{v}}}}} = \arctan \frac{1}{{2 \times {F^\# }}}, $ | (5) |
|
图 4 虚拟阵元延时参数计算及声场叠加 |
孔径角2θa决定了虚拟阵元的声场发射范围以及有效声场叠加的个数。已知声速c,任意样本点ii到虚拟阵元jj的延时参数为
| $ {\tau _{jj, ii}} = 2 \times \frac{{{Z_{\rm{v}}} \pm \sqrt {d\_{x^2} + d\_{z^2}} }}{c}。$ | (6) |
其中,“±”表示样本点在相应虚拟阵元的下方或者上方。
第二阶段采用逐点接收聚焦波束合成,参照式(6)可分别计算其他样本点的延时参数。则BF2合成的第n条扫描线数据为
| $ \begin{array}{l} {H_{n, ii}}\left( t \right) = \sum\limits_{jj = 1}^N {\omega \left( {jj} \right) \times {K_{jj, ii}} \times {S_{jj, ii}}\left( {t - {\tau _{jj, ii}}} \right), } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;ii = 1, 2, \cdots, M, \end{array} $ | (7) |
其中:ω(jj)为相应的幅度变迹系数;M为样本点总数;N为BF1所形成的扫描线总数;Sjj,ii(t)为波束合成器BF1所形成的第jj条扫描线上的第ii个样本点;τjj,ii为样本点ii相对于编号是jj的虚拟阵元的延时参数。
值得注意的是,目前大多数传统的超声成像系统都采用DAS波束合成方法,从上文可知,笔者提出的基于虚拟源阵元的双聚焦波束合成方法是在DAS基础之上,结合虚拟阵元的概念及合成孔径技术来实现的。而DAS波束合成方法以及合成孔径技术已趋于成熟,因此笔者提出的方法适合现有的超声成像系统。对于有限传感器阵列,随着样本点深度的增加,有效虚拟阵元个数将会超出实际虚拟阵元的个数。因此,越接近传感器阵列边缘的地方,有效样本个数不会再继续增加,此时侧向分辨率会略微下降。同时本算法假定所有成像点为静态点,对于动态成像点成像,原理方法基本类似,这里不做详述。
2 仿真与讨论Field Ⅱ[10-12]是基于线性系统空间响应原理对超声回波信号进行仿真,它的仿真结果与实际的成像结果很接近,已被国际上广泛认同为仿真超声系统的标准[13-15]。笔者利用Field Ⅱ进行点散射目标仿真实验,对比了传统动态接收聚焦DRF、合成聚焦SF以及基于虚拟阵元的双聚焦波束合成DFB算法,并重点分析了这3种算法在分辨率和探测深度方面的差异。
仿真过程中均采用定点发射和分段动态聚焦接收模式,成像采用线性阵列,阵元总数128,发射信号中心频率3.5 MHz,采样频率50 MHz,阵元中心间距为一个波长,声速1 540 m/s。信号仿真时加入了60 dB的高斯白噪声,成像的动态范围为40 dB[16]。设置虚拟源深度Zv=20 mm,聚焦系数F#=2,BF1的幅度变迹系数采用Hamming窗,BF2的幅度变迹系数采用Boxcar窗。为提高成像效果,采用了滑动子孔径技术,子孔径阵元数目为48。
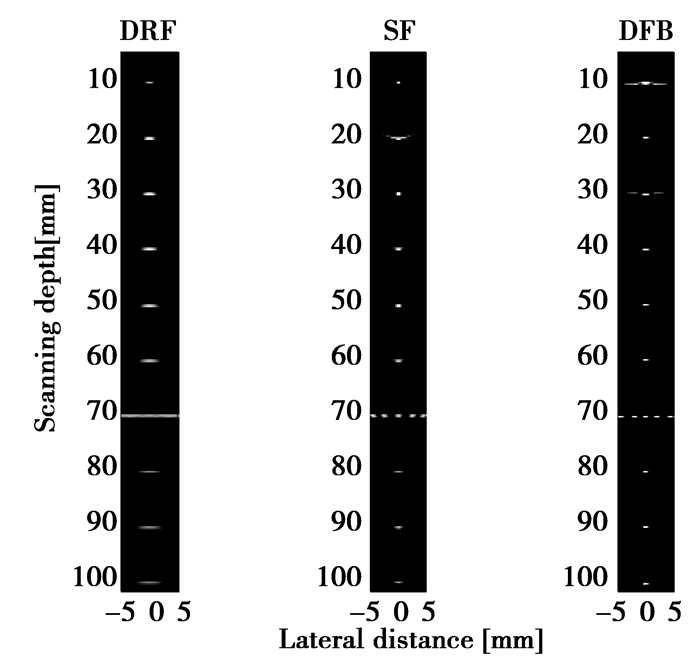
目标散射点共14个:其中深度70 mm处设定5个散射点,两相邻散射点横向间隔为2 mm,其余散射点分布在深度为10~100 mm的区域内,轴向间隔为10 mm。图 5为不同方法对不同深度散射点的成像结果。
|
图 5 动态范围40 dB时的不同深度散射点仿真成像 |
从图 5可以看出,传统的DRF波束合成算法侧向分辨率差,不能将深度70 mm处的5个散射点分辨开来,且随着深度增加,散射点的旁瓣逐渐增加;相比于DRF成像,SF算法虽然提高了侧向分辨率,但图像的对比度随着探测深度的增加而急剧下降,且系统复杂度方面远高于DRF;笔者提出的DFB算法,在提高图像的侧向分辨率和对比度方面都远远优于SF及DRF,系统复杂度略高于DRF,但远低于SF。
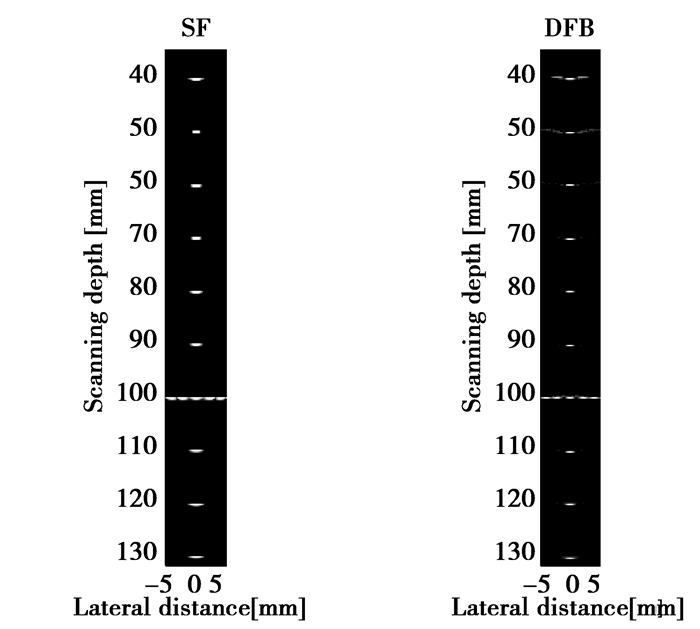
为说明笔者提出的DFB方法在一定程度上调和了探测深度和分辨率之间的矛盾,将目标散射点的位置在图 5的基础上整体沿z轴向下移动30 mm之后,仿真成像效果如图 6所示。由于图 5中DRF算法在70 mm处的分辨率太差,因此仅对SF和DFB方法做进一步仿真对比分析。
|
图 6 动态范围40 dB时散射点仿真成像(深度加深30 mm) |
从图 6可以看出,DFB算法的仿真成像结果中,目标点成像在z轴方向的宽度明显比SF算法成像的宽度细,即轴向分辨率DFB优于SF;对比图 5,在图 6中DFB及SF的侧向分辨率都有所下降,但DFB算法在100 mm处仍然可以清楚地分辨出轴上点以及轴外点,而SF算法在100 mm处所成的像几乎为一条直线,不能分辨出轴上点以及轴外点,侧向分辨率DFB远优于SF。因此DFB算法在一定程度上有效地调和了探测深度与分辨率之间的矛盾。
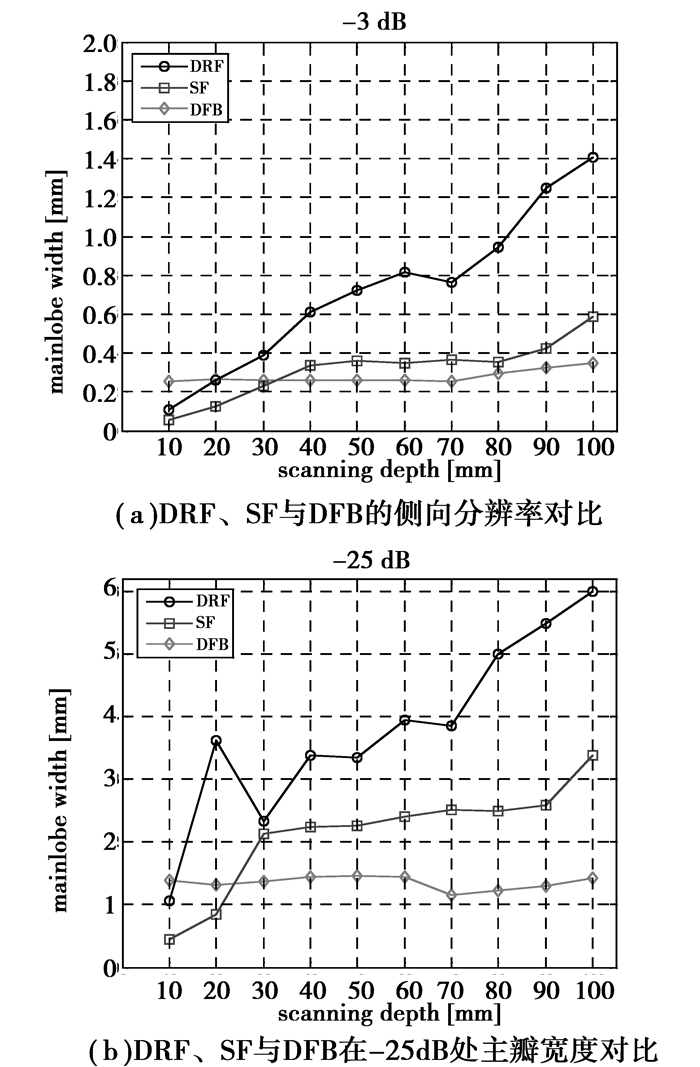
为进一步深入研究不同方法对图像质量的影响情况,图 7分别给出散射点回波数据的归一化幅值在-3 dB和-25 dB处主瓣宽度随探测深度变化的曲线。
|
图 7 DRF、SF与DFB的分辨率及能量衰减对比 |
从图 7可以看出,虽然DRF及SF算法在近场区域成像的侧向分辨率略优于DFB算法,但随着深度的增加,DFB算法在-3 dB处的主瓣宽度基本保持不变,成像效果明显优于DRF和SF。由于信号的主瓣宽度在-25 dB处仍然基本保持均匀,从而能量比较集中,因此,DFB算法能够有效地增加探测深度。
3 结语笔者将虚拟阵元技术引进到超声成像系统,利用2次延时叠加实现双聚焦波束合成超声成像。该方法本质就是利用2次延时叠加进行多个重叠声场的相关有效信息的提取,间接增加了接收阵元数目,从而增加声波信号的信息量和能量,使得成像效果获得大幅度提高。静态点散射目标的成像实验表明:与传统DRF及SF算法相比,该方法的分辨率在一定范围内不会随着探测深度的增加而急剧下降,在一定程度上解决了分辨率与探测深度之间的矛盾,并且可以针对不同应用场合来调节虚拟阵元的位置Zv以及聚焦系数F#,实现高质量的超声成像。
| [1] | 彭虎. 超声成像算法导论[M]. 合肥: 中国科学技术大学出版社, 2008. |
| [2] | 胡鹏. 虚拟阵元波束形成方法研究[D]. 西安: 西北工业大学硕士学位论文, 2006. |
| [3] | 冯若. 超声手册[M]. 南京: 南京大学出版社, 1999. |
| [4] |
王平, 许琴, 王伟明, 等.
超声成像系统的动态孔径控制方法[J]. 重庆大学学报, 2011, 34(3): 89–93.
WANG Ping, XU Qin, WANG Weiming, et al. The method of dynamic aperture control technology based on ultrasound imaging system[J]. Journal of Chongqing University, 2011, 34(3): 89–93. DOI:10.11835/j.issn.1000-582X.2011.03.015 (in Chinese) |
| [5] | Ye L, Jensen J A. Synthetic aperture flow imaging using a dual stage beamformer approach[C]//Proceedings of the 2010 IEEE Ultrasonics Symposium, October 11-14, 2010, San Diego, CA. Piscataway:IEEE Press, 2010:1924-1927. |
| [6] | Frazier C H, O'Brien W D. Synthetic aperture techniques with a virtual source element[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1998, 45(1): 196–207. DOI:10.1109/58.646925 |
| [7] | Passmann C, Ermert H. A 100-MHz ultrasound imaging system for dermatologic and ophthalmologic diagnostics[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1996, 43(4): 545–552. DOI:10.1109/58.503714 |
| [8] | Jacob K. Synthetic aperture sequential beamforming and other beamforming techniques in ultrasound imaging[D]. Denmark:Technical University of Denmark, 2008. |
| [9] | Hemmsen M C. Image processing in medical ultrasound[D]. Denmark:Technical University of Denmark, 2011. |
| [10] | Jensen J A. Users' guide for the field Ⅱ program[D]. Denmark:Technical University of Denmark, 2011. |
| [11] | Jensen J A. Field:a program for simulating ultrasound systems[J]. Medical Biological Engineering, 1996, 34. |
| [12] | Hemmsen M C, Kortbek J, Nikolov S I, et al. Simulation of high quality ultrasound imaging[C]//Proceedings of the 2010 IEEE Ultrasonics Symposium, October 11-14, 2010, San Diego, CA. Piscataway:IEEE Press, 2010:1739-1742. |
| [13] | Hergum T, Langeland S, Remme E W, et al. Fast ultrasound imaging simulation in K-space[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(6): 1159–1167. DOI:10.1109/TUFFC.2009.1158 |
| [14] | Vignon F, Burcher M R. Capon beamforming in medical ultrasound imaging with focused beams[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2008, 55(3): 619–628. DOI:10.1109/TUFFC.2008.686 |
| [15] | Nilsen C I C, Hafizovic I. Beamspace adaptive beamforming for ultrasound imaging[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(10): 2187–2197. DOI:10.1109/TUFFC.2009.1301 |
| [16] | Asl B M, Mahloojifar A. Contrast enhancement and robustness improvement of adaptive ultrasound imaging using forward-backward minimum variance beamforming[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, Frequency Control, 2011, 58(4): 858–867. DOI:10.1109/TUFFC.2011.1880 |
 2013, Vol. 36
2013, Vol. 36

