1b. 重庆大学 资源及环境科学学院, 重庆 400044;
2. 四川省威达煤业有限责任公司, 四川 叙永 646400
1b. College of Resources and Environment, Chongqing University, Chongqing 400044, China;
2. Sichuan WeiDa Coal Industry Limited Company, Xuyong, Sichuan 646400, China
沿空留巷作为先进的无煤柱护巷技术,已经在许多煤矿中得到广泛应用[1-12]。针对沿空留巷时的围岩控制,国内外学者取得了许多相关研究成果。孙恒虎[13]认为沿空留巷顶板仅在自身重力作用下以主动垮落为主,将顶板岩层简化为三边或四边支承的矩形叠加板,提出顶板载荷的条带分割法。在此基础上,孙立亚等[14]根据井巷围岩的弹塑性应力分析,提出缓倾斜煤层沿空留巷围岩控制理论。李化敏[15]认为顶板活动过渡期为留巷顶板活动最剧烈也是最危险的时期,沿空留巷顶板岩层控制设计应以该时期充填体所需的支护阻力为基础。华心祝等[16]提出巷内采用锚杆、巷旁采用锚索的主动加强支护方式,建立了考虑巷帮煤体承载作用和锚杆、锚索加强作用的沿空留巷力学模型,提出支护-煤体-顶板共同承载体系。阚甲广等[17]将工程实践中接触到的留巷顶板分为厚层直接顶、薄层直接顶和无直接顶3种类型,利用叠加连续层板模型,考虑巷帮煤体承载作用和导致顶板垮落诱因,得出了3种顶板条件下的巷旁支护阻力计算公式。文志杰等[18]运用“实用矿山压力控制理论”建立了沿空留巷开采灾害系统模型,提出了无煤柱沿空留巷“大、小结构理论”,修正了“内应力场”范围计算方法,建立了“给定变形”、“限定变形”2种留巷结构力学模型。英国学者Whittaker等[19]将采场矿压研究的Wilson模型加以发展,利用岩体结构静力学关系提出了分离岩块力学模型(Detached Block Theory)。英国南威尔斯大学Smart等[20]提出了倾斜岩梁理论(Roof Beam Tilt Theory),这种方法的基本思想是通过巷旁支护限制巷道煤体一侧到采空区边缘之间的顶板下沉量,提出了顶板倾斜角和转动支点位置是巷旁支护设计两个重要参数的观点。
但前人的研究多是基于水平建立的力学模型,也未曾对倾斜煤层机巷和风巷沿空留巷时的受力情况作对比分析。笔者在条带分割法的基础上,考虑煤层倾角影响,分别建立沿空留机巷和沿空留风巷时顶板活动前、后期的力学模型,并进行对比分析。
1 顶板活动前期力学结构模型 1.1 沿空留机巷模型当采用区段下行式开采时,沿空留巷将维护本区段机巷作为下区段的回风巷。此时,巷旁支护是维护本区段机巷的高帮。
采场顶板岩层力学结构模型见图 1。其中,图 1(a)为顶板初次垮落时的4边支承矩形板;图 1(b)为顶板周期垮落时的3边支承矩形板。图中La为工作面长度,Lb、L′b分别为工作面顶板初次来压步距和周期来压步距,a为巷道维护宽度,b为巷旁支护宽度。顶板载荷仍然按条带分割[4],阴影部分由沿空留巷时的巷内支护体及巷旁支护共同承担,其中4边支承矩形板在中心部分弯矩最大,3边支承矩形板在自由边弯矩最大。从图 1(a)和图 1(b)可知,截取弯矩最大部分单位宽度的板条,两种结构模型是一致的,得到图 1(c)所示的OO′ABCD顶板梁结构。设顶板梁自重载荷集度为q,按条带分割后,载荷只作用在OA和CD两段,O点为固定边界,巷旁支护阻力用支护体对顶板的等效集中力P表示,并作用于A点;岩层破断时,破断处的极限弯矩均为MP1,受力情况见图 1(d)。在初始阶段,岩层下沉变形很小,层面应力及摩擦力引起的弯矩忽略不计。
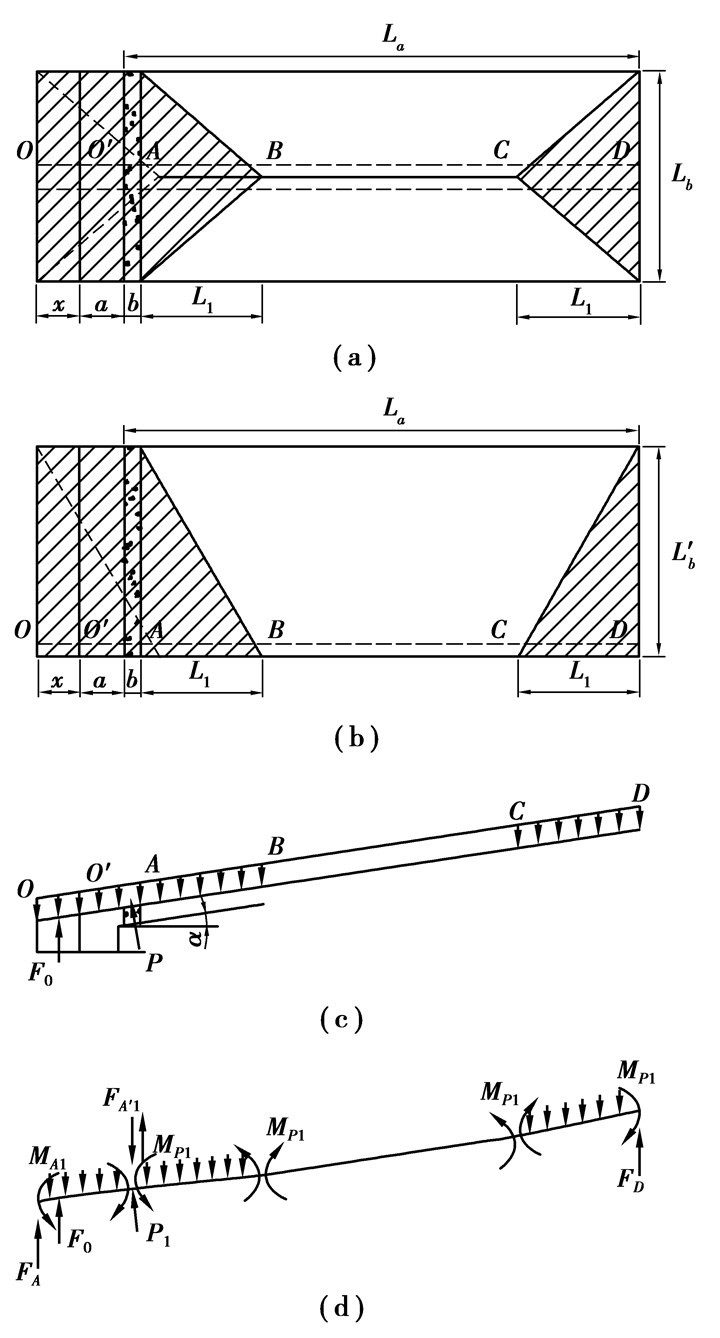
|
图 1 沿空留巷巷旁支护阻力计算模型(第1层) |
随着工作面的推进,顶板梁结构将以煤壁一侧为支点向采空区侧发生旋转下沉,煤壁上方岩层将从固支边界转变为简支边界。相对岩层而言,煤层强度较低。见图 1,一般认为煤壁O′点不适于作为顶板梁旋转支点,应偏移至煤壁深处稳定区边界的O点。当煤壁上方顶板为固支边界时,顶板岩层具有自承能力,有利于巷旁支护承载;如果成为简支边界,则顶板岩层丧失自承能力,巷道及巷旁上方的顶板载荷主要由巷旁支护承担。因此,保证顶板和巷道一侧煤壁的完整性,使煤壁上方顶板岩层处于固定边界,可以提高顶板岩层自承能力,有利于降低顶板活动前期的巷旁支护阻力。
从第1层顶板开始进行沿空留巷的受力分析。在极限条件下,用平衡法对图 1(d)中各段求解,则第1层顶板
AB段:
| $ \sum {{F_y}} = 0,{F_{A1}} - {q_1}{L_1} = 0, $ | (1) |
| $ \sum M = 0,2{M_{P1}} - {q_1}L_1^2/2 = 0; $ | (2) |
OA段:
| $ \begin{array}{l} {P_{1机}}\frac{{x + a + b/2}}{{\cos \alpha }} + {M_{A1}} + \frac{1}{2}{F_0}x - \\ \frac{{{q_1}}}{2}{\left( {x + a + b} \right)^2} - {F_{A1}}\left( {x + a + b} \right) - {M_{P1}} = 0。\end{array} $ | (3) |
将以上三式联立求解得:
| $ \begin{array}{l} {P_{1机}}\frac{{x + a + b/2}}{{\cos \alpha }} = \frac{{{q_1}}}{2}{\left( {x + a + b} \right)^2} + \\ {q_1}{L_1}\left( {x + a + b} \right) + {M_{P1}} - {M_{A1}} - \frac{1}{2}{F_0}x。\end{array} $ | (4) |
式中:FA1为顶板梁在A点破断产生的下向剪力,N;q1=γ1h1/cosα为岩层自重集度,N/m2;L1为岩层破断特征尺寸[13],m;γ1为第一层顶板岩层容重,N/m3;h1为第一层顶板岩层厚度,m;α为煤层倾角;P1机为机巷留巷巷旁支护前期所需的最小支护阻力,N;x为煤壁松动区宽度,m;a为巷道维护宽度,m;b为巷旁支护宽度,m;MA1为岩层最大抗弯弯矩,N·m;F0为巷旁煤体对顶板的支撑力,N;MP1为岩层破断时的最大弯矩,N·m,在极限条件下,MP1=MA1。
巷旁顶板第1层顶板岩层的切顶阻力主要是人工支护提供的,而第2层以上的岩层所需的切顶阻力是人工支护和已垮岩层残留边界共同作用的结果。巷旁顶板第二层岩层受力情况如图 2所示。
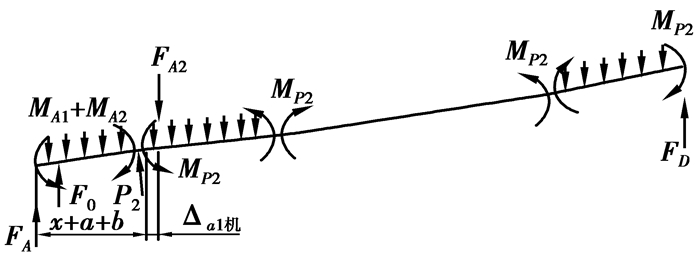
|
图 2 沿空留巷支护阻力计算模型(第2层) |
对于第2层,切顶支护阻力计算式为:
| $ \begin{array}{*{20}{c}} {{P_{2机}}\frac{{x + a + b/2}}{{\cos \alpha }} = \sum\limits_{i = 1}^2 {\frac{{{\gamma _i}{h_i}}}{{2\cos \alpha }}{{\left( {x + a + b + \Delta {a_{1机}}} \right)}^2}} + }\\ {\sum\limits_{i = 1}^2 {{F_{Ai}}\left( {x + a + b + \Delta {a_1}} \right)} + {M_{P2}} - }\\ {\sum\limits_{i = 1}^2 {{M_{Ai}}} - \frac{1}{2}{F_0}x。} \end{array} $ | (5) |
其中:
| $ \Delta {a_{1机}} = \sum\limits_{j = 0}^1 {\frac{{{h_j}\sin {\theta _j}}}{{\cos \left( {{\theta _j} + \alpha } \right)}}} 。$ | (6) |
式中:Δa1机为第2层顶板岩层受第1层岩层残留边界影响破断时增加的水平宽度;hj为第j层顶板岩层厚度,m;θj为第j层顶板岩层破断角[21],即顶板岩层破断线与竖直方向的夹角。且规定,θ0=0,hj=0。
同理,第m层切顶阻力计算式为:
| $ \begin{array}{*{20}{c}} {{P_{m机}}\frac{{x + a + b/2}}{{\cos \alpha }} = \sum\limits_{i = 1}^m {\frac{{{\gamma _i}{h_i}}}{{2\cos \alpha }}{{\left[ \begin{array}{l} x + a + b + \\ \sum\limits_{j = 0}^{m - 1} {\frac{{{h_j}\sin {\theta _j}}}{{\cos \left( {{\theta _j} + \alpha } \right)}}} \end{array} \right]}^2}} + }\\ {\sum\limits_{i = 1}^m {{F_{Ai}}\left[ {x + a + b + \sum\limits_{j = 0}^{m - 1} {\frac{{{h_j}\sin {\theta _j}}}{{\cos \left( {{\theta _j} + \alpha } \right)}}} } \right]} + }\\ {{M_{Pm}} - \sum\limits_{i = 1}^m {{M_{Ai}}} - \frac{1}{2}{F_0}x。} \end{array} $ | (7) |
式中:等号右边第1项是由未垮落顶板岩层自重引起的弯矩;第2项是垮落顶板下向剪力产生的弯矩;第3项是第m层顶板岩层破断时的最大弯矩;第4项是第1~m层岩层的抗弯弯矩之和;第5项是松动煤壁对顶板提供的支撑弯矩。等式右边前3项所产生的围岩载荷要由人工支护及煤壁支护阻力来平衡,而第4项和第5项帮助巷旁支护承载,形成支护煤体顶板共同的承载体系。
由式(7)可以看出,当巷道维护宽度不变,煤层倾角α增大时,所需的巷旁支护阻力将随之增大。当煤层倾角α增大到采空区冒落矸石自然安息角φ0以上时,采空区冒落矸石因自重沿底板向机巷侧下滑堆积,将对残留顶板岩层产生一定的支撑力T,有利于减小巷旁支护阻力,如图 3所示。
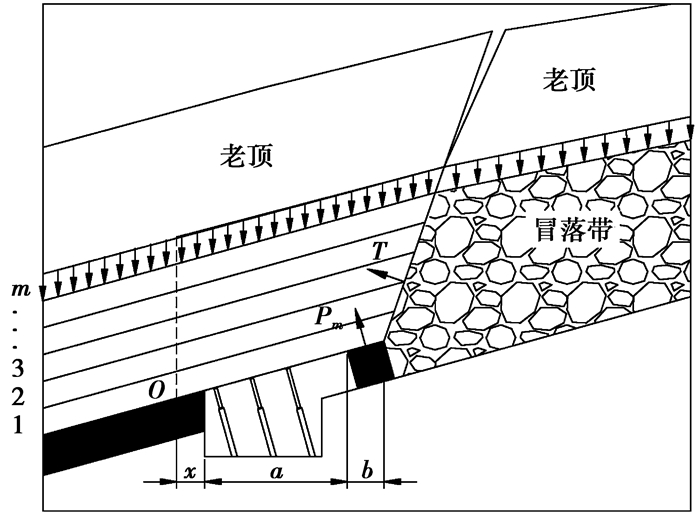
|
图 3 倾斜煤层机巷沿空留巷前期巷旁力学结构模型 |
巷道一侧完整煤体对顶板岩层的支承力所产生的弯矩,其计算较为复杂。从安全角度,也便于简化计算,可假设松动区内煤体以均布载荷的形式作用于顶板岩层[16],均布载荷的大小选用煤体的残余抗压强度σ′c,则
| $ {F_0} = {{\sigma '}_{\rm{c}}}x。$ | (8) |
当采用区段上行式开采时,沿空留巷将维护本区段的回风巷作为上区段的机巷。此时,巷旁支护是维护本区段回风巷的矮帮,见图 4。此时,顶板上部岩层受下部岩层残留边界影响破断而增加的水平宽度有所不同。通过几何关系,可得:
| $ \Delta {a_{i风}} = \sum\limits_{j = 0}^i {\frac{{{h_j}\sin {\theta _j}}}{{\cos \left( {{\theta _j} - \alpha } \right)}}} 。$ | (9) |
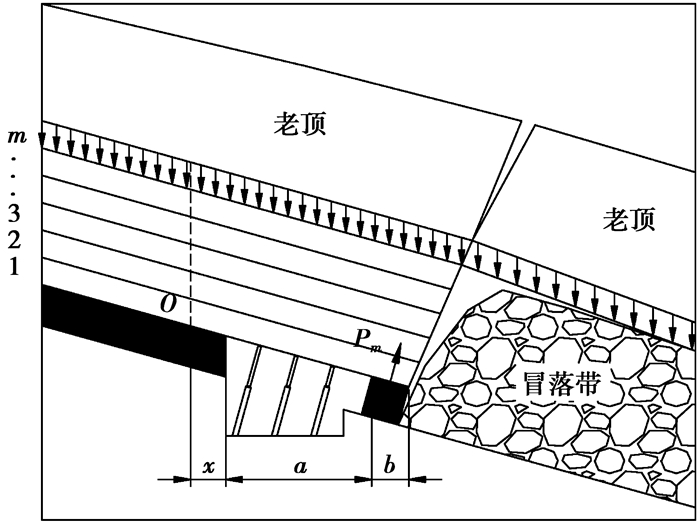
|
图 4 倾斜煤层风巷沿空留巷前期巷旁力学结构模型 |
式中,Δai风为沿空留风巷时,第i+1层顶板受以下i层顶板残留边界影响破断而增加的水平宽度。
与沿空留机巷类似,在沿空留风巷时,顶板活动前期的巷旁支护阻力计算公式为:
| $ \begin{array}{*{20}{c}} {{P_{m风}}\frac{{x + a + b/2}}{{\cos \alpha }} = \sum\limits_{i = 1}^m {\frac{{{\gamma _i}{h_i}}}{{2\cos \alpha }}\left[ {x + a + b + } \right.} }\\ {{{\left. {\sum\limits_{j = 0}^{m - 1} {\frac{{{h_j}\sin {\theta _j}}}{{\cos \left( {{\theta _j} - \alpha } \right)}}} } \right]}^2} + }\\ {\sum\limits_{i = 1}^m {{F_{Ai}}\left[ {x + a + b + \sum\limits_{j = 0}^{m - 1} {\frac{{{h_j}\sin {\theta _j}}}{{\cos \left( {{\theta _j} - \alpha } \right)}}} } \right]} + }\\ {{M_{Pm}} - \sum\limits_{i = 1}^m {{M_{Ai}}} - \frac{1}{2}{F_0}x。} \end{array} $ | (10) |
式中,Pm风为沿空留风巷顶板活动前期巷旁支护所需的最小支护阻力。
2 顶板活动后期力学结构模型 2.1 极限切顶高度顶板极限切顶高度,是直接顶垮落后能充满采空区时所切落的顶板高度,其大小与岩层碎胀性和采高有关系:
| $ H = \sum\limits_{i = 0}^m {{h_i}} = {m_0}/\left( {{K_s} - 1} \right)。$ | (11) |
式中:H为充满采空区的直接顶切顶高度;Ks为垮落岩层初始碎胀系数,一般取1.25~1.35;m0为煤层开采高度;m为顶板极限切落层数。
当m层顶板岩层被切断后能填满采空区时,第m+1层及以上岩层将不再被切断。随着工作面的推移,采空区上位老顶旋转下沉逐渐压实下位冒落带。此时,巷旁支护阻力达到最大值,顶板活动前期控顶高度内未垮落顶板岩层受到挤压,当超过其承载极限时,便产生“二次破断”。老顶旋转下沉过程中将迫使二次破断带顶板下沉,此时需要支护体有一定的可缩量来退让,否则支护体或者煤壁易被压坏。当巷道维护宽度一定时,老顶下沉量与地质条件及煤层采高有关,通过几何关系换算可得到支护体处的顶板下沉量,即支护体所需的可缩量。
2.2 顶板下沉量支护体对顶板下沉量的控制主要是通过改变巷道顶板和离层带的旋转倾角而实现的。设错动离层带的倾角为α2,巷道顶板的倾角为α1,a为巷道维护宽度,L为离层带长度,采空区下沉量为SB,巷旁支护体处顶板下沉量为SA,巷道没帮的压缩量SA′。可根据图 5的几何关系分别得沿空留机巷(图 5(a))和沿空留风巷(图 5(b))时支护体所需可缩量。
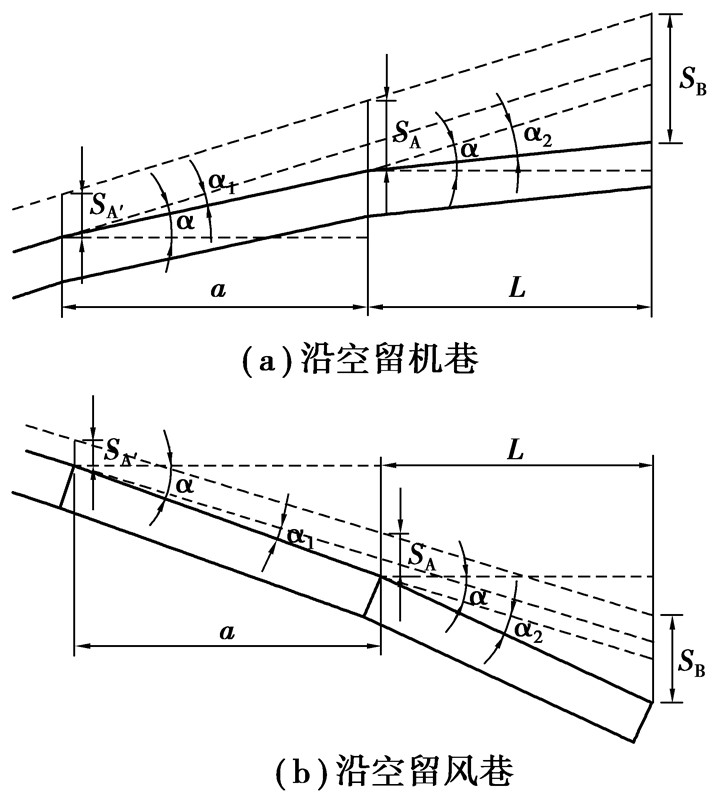
|
图 5 沿空留巷顶板下沉量几何关系 |
| $ {S_{A机}} = {S_{A'}} + a\frac{{\sin {\alpha _{1机}}}}{{\cos \alpha \cos \left( {\alpha - {\alpha _{1机}}} \right)}}, $ | (12) |
| $ {S_{A机}} = {S_B} - L\frac{{\sin {\alpha _{2机}}}}{{\cos \alpha \cos \left( {\alpha - {\alpha _{2机}}} \right)}}, $ | (13) |
式中:SA机为沿空留机巷时巷旁支护体处顶板下沉量;α2机为沿空留机巷时错动离层带的倾角,α1机为沿空留机巷时巷道顶板的倾角。
2.2.2 沿空留风巷时顶板各处下沉量关系| $ {S_{A风}} = {S_{A'}} + a\frac{{\sin {\alpha _{1风}}}}{{\cos \alpha \cos \left( {\alpha + {\alpha _{1风}}} \right)}}, $ | (14) |
| $ {S_{A风}} = {S_B} - L\frac{{\sin {\alpha _{2风}}}}{{\cos \alpha \cos \left( {\alpha + {\alpha _{2风}}} \right)}}, $ | (15) |
式中:SA风为沿空留风巷时巷旁支护体处顶板下沉量;α2风为沿空留风巷时错动离层带的倾角,α1风为沿空留风巷时巷道顶板的倾角。
SA′受煤质和顶板条件的直接影响,顶板越坚硬,煤质越软,SA′越大,反之越小。
SB主要与冒落区岩层碎胀性及煤层采高有关,其大小可由下式计算,
| $ {S_B} = \frac{{{K_{\rm{s}}} - {K_{\rm{c}}}}}{{{K_{\rm{s}}} - 1}} \cdot \frac{{{m_0}}}{{\cos \alpha }} $ | (16) |
式中:Kc为冒落带矸石压实后的碎胀系数,一般取1.05;其他符号同前。
当SB、SA′、a、L为定值时,由式(12)~(15)可以看出,提高α2和减小α1可以减小SA。这也表明,对比较完整的顶板,通过减小巷道顶板的旋转角度和增加离层带岩层的下沉角度,可以减小沿空留巷时巷旁支护处的顶板下沉量。
2.3 沿空留机巷模型随着冒落带被压实,老顶旋转下沉趋于稳定,且破断岩块之间仍然保持力学联系,形成具有自稳平衡的“砌体梁”结构[22],其下部出现卸压区域。此时,二次破断顶板处于简支边界,如图 6所示。因此,在顶板活动后期,巷旁支护阻力主要用来平衡上覆二次破缎带岩层自重在O点产生的力矩。
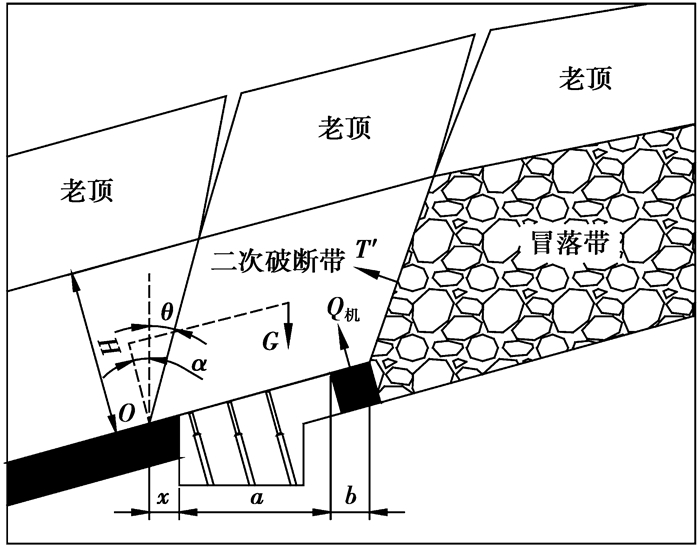
|
图 6 倾斜煤层机巷沿空留巷后期巷旁力学结构模型 |
文献[4]认为顶板活动后期所需巷旁支护阻力应能平衡式(7)或式(10)等号右边第一项岩层自重载荷产生的弯矩,其假设条件是二次破断线基于O点竖直向上。但大量现场观测和实验室研究表明[21],顶板岩层在二次破断时仍会形成一定破断角。考虑极限情况,二次破断时的岩层破断角与切顶时相等(由于边界条件的限制,其破断角将介于0到θj之间),即将二次破断带顶板岩层近似看作平行四边形,其自重载荷等效为作用于其形心的集中力G。将其分解为垂直和平行层面的两个分量Gn和Gt,其中Gn对O点的力矩主要由巷旁支护来平衡,而Gt对O点的力矩指向煤壁一侧,对下侧煤壁产生一定压力,有利于减小巷旁支护阻力。
由于顶板旋转下沉,使巷帮煤体破坏,可认为其不再具有承载能力,故在计算时忽略巷旁煤体提供的支撑力矩。如图 5所示。对O点取矩,力学平衡方程为:
| $ \begin{array}{*{20}{c}} {{Q_{机}}\frac{{x + a + b/2}}{{\cos \alpha }} = \frac{1}{2}G\cos \alpha \left[ {H\tan \left( {\theta + \alpha } \right) + } \right.}\\ {\left. {\frac{{x + a + b}}{{\cos \alpha }}} \right] - \frac{1}{2}GH\sin \alpha 。} \end{array} $ | (17) |
式中:Q机为机巷留巷巷旁支护后期所需的最小支护阻力;G为二次破断带岩层的总重力在形心的等效力;H为顶板切断岩层总厚度;θ为顶板岩层平均破断角。
依据式(12)求解顶板活动后期巷旁支护阻力的计算结果较实际偏小,但计算方法简便,在运用时可适当修正,以便满足安全需要。
当煤层倾角α大于采空区冒落矸石自然安息角φ0时,冒落矸石因自重沿底板向支护体一侧下滑堆积,对残留顶板岩层产生支撑力T′(如图 6所示),有利于减小巷旁支护阻力。
二次破断带顶板岩层自重集中力G可按下式计算:
| $ G = \frac{{x + a + b}}{{\cos \alpha }}\gamma H。$ | (18) |
将式(18)代入式(17)化简得:
| $ \begin{array}{*{20}{c}} {{Q_{机}}\left( {x + a + \frac{b}{2}} \right) = \frac{{{{\left( {x + a + b} \right)}^2}\gamma H}}{2} + }\\ {\frac{{\left( {x + a + b} \right)\gamma {H^2}\sin \theta }}{{2\cos \left( {\theta + \alpha } \right)}}。} \end{array} $ | (19) |
沿空留风巷时,顶板岩层自重分量Gn和Gt对O点的力矩均由巷旁支护来平衡,见图 7。
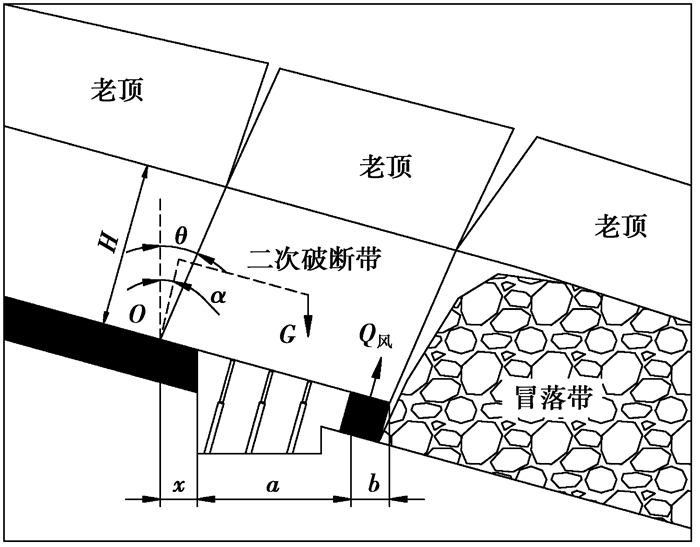
|
图 7 倾斜煤层风巷沿空留巷后期巷旁力学结构模型 |
同理,对O点取矩,模型的力学平衡方程为:
| $ \begin{array}{*{20}{c}} {{Q_{风}}\frac{{x + a + b/2}}{{\cos \alpha }} = \frac{1}{2}G\cos \alpha \left[ {H\tan \left( {\theta - \alpha } \right) + } \right.}\\ {\left. {\frac{{x + a + b}}{{\cos \alpha }}} \right] + \frac{1}{2}GH\sin \alpha 。} \end{array} $ | (20) |
将式(18)代入式(20)化简得:
| $ \begin{array}{*{20}{c}} {{Q_{风}}\left( {x + a + \frac{b}{2}} \right) = \frac{{{{\left( {x + a + b} \right)}^2}\gamma H}}{2} + }\\ {\frac{{\left( {x + a + b} \right)\gamma {H^2}\sin \theta }}{{2\cos \left( {\theta - \alpha } \right)}}。} \end{array} $ | (21) |
式中,Q风为顶板活动后期沿空留风巷巷旁支护所需的最小支护阻力。
2.5 巷旁支护阻力对比分析比较前面的沿空留机巷和沿空留风巷力学结构模型分析结果,不同的区段接替顺序时巷旁支护受力存在如下特点:
1) 当巷道维护宽度一定,若采用沿空留机巷,由式(7)、(19)可知,顶板活动前、后期巷旁支护阻力随煤层倾角的增大而增加;若采用沿空留风巷,由式(10)、(21)可知,顶板活动前、后期巷旁支护阻力随煤层倾角的增大而减小。
2) 当煤层倾角α增大到采空区冒落矸石自然安息角φ0以上时,应考虑矸石下滑堆积对残留顶板的作用。采用沿空留机留巷,冒落矸石向支护体一侧下滑堆积,对残留顶板将产生一定支撑作用,有利于降低巷旁支护阻力;采用沿空留风巷,冒落矸石向采空区堆积,不再对残留顶板产生支撑作用。
3) 机巷和风巷沿空留巷时所需切顶阻力大小的差异主要来自Δai机和Δai风,令
| $ \begin{array}{*{20}{c}} {{R_{\Delta a}} = \Delta {a_{i机}} - \Delta {a_{i风}} = }\\ {\sum\limits_{j = 0}^i {\frac{{4{h_j}{{\sin }^2}{\theta _j}\sin \alpha }}{{\cos \left( {{\theta _j} + \alpha } \right)\cos \left( {{\theta _j} - \alpha } \right)}}。} } \end{array} $ | (22) |
若不考虑其他因素的影响,RΔa恒大于等于零,即表明采用沿空留风巷的巷旁支护阻力小于沿空留机巷的巷旁支护阻力。
4) 比较式(17)、(20)可知,采用沿空留机巷时,顶板自重分量Gt作用倾斜向下,使顶板岩层处于受压状态,有利于保持其完整性,但对巷道下侧煤壁造成较大压力,需要加强煤壁支护;采用沿空留风巷时,顶板自重分量将指向下侧的采空区,顶板处于受拉状态,对于软弱破碎顶板,不利于维护其完整性。
5) 顶板活动后期的巷旁支护阻力小于前期支护阻力。因此,巷旁支护设计应以前期切顶支护力为依据,且在顶板活动过渡期,巷旁支护体应有一定的可缩量,以便适应老顶的下沉,否则,支护体易被压坏。
3 算例国内某煤矿[2]2号煤层1528综采工作面对运输巷采用沿空留巷方案,用作相邻1526综采工作面的回风巷。1528综采工作面的采深291~315 m,煤层厚度2.2~2.5 m,平均倾角15°;直接顶为泥质粉砂岩,致密性脆,属中等稳定顶板;基本顶为细砂岩,属稳定顶板。巷道维护宽度3.6 m,煤壁松动范围宽度2.5 m,巷旁支护宽度按1 m计算。
根据现场实测,工作面周期来压步距15 m,顶板岩层破断角θ平均30°,顶板岩层抗拉强度8 MPa。煤层采高2.5 m,由式(11)计算,极限切顶高度为10 m。为简化计算,将顶板岩层等厚划分为10层,每层厚度为1.0 m,容重为25 kN/m3,且每层岩层破断角相等,取其平均值θ=30°。
将以上数据代入式(7)和式(19),得到沿空留机巷时巷旁支护前期支护阻力为5 001 kN/m,后期支护阻力为1 906 kN/m。
将以上数据带入式(10)和式(21),得到沿空留风巷时前期巷旁支护阻力为4 227 kN/m,后期支护阻力为1 651 kN/m。
计算结果表明,在不考虑采空区冒落矸石对顶板作用时,采用沿空留风巷顶板活动前、后期巷旁支护阻力均小于沿空留机巷时的支护阻力,则在沿空留巷巷旁支护设计时,不仅考虑要考虑煤层倾角、厚度和煤岩性质,还应该考虑区段下行式或上行式的接替顺序。
4 结论针对不同区段接替顺序的沿空留巷围岩力学作用过程,得到如下的主要研究结果:
1) 针对倾斜煤层机巷和风巷分别采用沿空留巷条件,分别建立了顶板活动前、后期巷旁支护的力学结构模型,并给出了相应的巷旁支护阻力计算公式。
2) 沿空留机巷和沿空留风巷的对比分析表明,在煤层倾角较小时,沿空留风巷的巷旁支护所需支护阻力较沿空留机巷的小;当煤层倾角较大时,由于采空区冒落矸石下滑堆积支撑顶板,有利于减小沿空留机巷所需的巷旁支护阻力。
3) 由于沿空留机巷时顶板受压和巷道下侧煤壁受压,有利于保持巷道顶板的完整性,但是,需加强煤壁支护,防止煤壁进一步挤压剪切破坏;沿空留风巷留巷时,顶板受拉,不利于保持顶板的完整性,需要加强顶板维护。
| [1] |
黄艳利, 张吉雄, 张强, 等.
综合机械化固体充填采煤原位沿空留巷技术[J]. 煤炭学报, 2011, 36(10): 1624–1628.
HUANG Yanli, ZHANG Jixiong, ZHANG Qiang, et al. Technology of gob-side entry retaining on its original position in fully-mechanized coalface with solid material backfilling[J]. Journal of China Coal Society, 2011, 36(10): 1624–1628. (in Chinese) |
| [2] |
赵庆彪, 刘长武.
组合支架切顶巷旁自行充填矸石墙体留巷试验[J]. 煤炭学报, 2011, 36(6): 891–896.
ZHAO Qingbiao, LIU Changwu. Remain tunnel experiment of combination support roof cutting beside of self-filling waste wall[J]. Journal of China Coal Society, 2011, 36(6): 891–896. (in Chinese) |
| [3] |
唐建新, 胡海, 涂兴东, 等.
普通混凝土巷旁充填沿空留巷试验[J]. 煤炭学报, 2010, 35(9): 1425–1429.
TANG Jianxin, HU Hai, TU Xingdong, et al. Experimental on roadside packing gob-side entry retaining for ordinary concrete[J]. Journal of China Coal Society, 2010, 35(9): 1425–1429. (in Chinese) |
| [4] |
康红普, 牛多龙, 张镇, 等.
深部沿空留巷围岩变形特征与支护技术[J]. 岩石力学与工程学报, 2010, 29(10): 1977–1987.
KANG Hongpu, NIU Duolong, ZHANG Zhen, et al. Deformation characteristics of surrounding rock and supporting technology of gob-side entry retaining in deep coal mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(10): 1977–1987. (in Chinese) |
| [5] |
马立强, 张东升, 陈涛, 等.
综放巷内充填原位沿空留巷充填体支护阻力研究[J]. 岩石力学与工程学报, 2007, 26(3): 544–550.
MA Liqiang, ZHANG Dongsheng, CHEN Tao, et al. Study on packing body supporting resistance of enter-in packing for in-situ gob-side entry retaining in fully-mechanized top-coal caving mining face[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 544–550. (in Chinese) |
| [6] |
朱川曲, 张道兵, 施式亮, 等.
综放沿空留巷支护结构的可靠性分析[J]. 煤炭学报, 2006, 31(2): 141–144.
ZHU Chuanqu, ZHANG Daobing, SHI Shiliang, et al. Reliability analysis on support structure of gob-side entry retaining in fully-mechanized caving face[J]. Journal of China Coal Society, 2006, 31(2): 141–144. (in Chinese) |
| [7] | Zhu C Q, Miao X X, Liu Z. Mechanical analysis on deformation of surrounding rock with road-in packing of gob-side entry retaining in fully-mechanized sub-level caving face[J]. Journal of Coal Science and Engineering, 2008, 14(1): 24–28. DOI:10.1007/s12404-008-0005-5 |
| [8] | Dong Y F, Wang Y G. Application of full-length anchor support technology in a large-section roadway under complicated geological conditions[J]. Journal of Coal Science and Engineering, 2012, 18(1): 10–13. DOI:10.1007/s12404-012-0102-3 |
| [9] | Wang Y J, Zhao Q B, Sun L Z. Controlling entry in soft rock with natural support strength, strikesill, etc[J]. Journal of Coal Science and Engineering, 2008, 14(2): 186–189. DOI:10.1007/s12404-008-0038-9 |
| [10] | Wang W J, Zhu Y J, Li S Q, et al. The principle of stability control of surrounding rock-bearing structures in high stress soft rock roadways[J]. Journal of Coal Science and Engineering, 2009, 15(1): 24–27. DOI:10.1007/s12404-009-0104-y |
| [11] | Kidybiński A. Design criteria for roadway supports to resist dynamic loads[J]. International Journal of Mining and Geological Engineering, 1986, 4(2): 91–109. DOI:10.1007/BF01560669 |
| [12] | Hao C Y, Wang J R, Deng C B, et al. Numerical simulation and actual research on safety and suitable position of roadway driving along next goaf[J]. Journal of Coal Science and Engineering, 2010, 16(2): 125–128. DOI:10.1007/s12404-010-0203-9 |
| [13] | 孙恒虎, 赵炳利. 沿空留巷的理论与实践[M]. 北京: 煤炭工业出版社, 1993. |
| [14] |
孙立亚, 胡仁山, 王学启.
缓斜煤层沿空留巷围岩控制理论研究[J]. 矿山压力与顶板管理, 1997(Z1): 143–145.
SUN Liya, HU Renshan, WANG Xueqi. Mechanism of surrounding rock control of gently inclined coal seam for gob-side entry[J]. Ground Pressure and Strata Control, 1997(Z1): 143–145. (in Chinese) |
| [15] |
李化敏.
沿空留巷顶板岩层控制设计[J]. 岩石力学与工程学报, 2000, 19(5): 651–654.
LI Huamin. Control design of roof rocks for gob-side entry[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(5): 651–654. (in Chinese) |
| [16] |
华心祝, 马俊枫, 许庭教.
锚杆支护巷道巷旁锚索加强支护沿空留巷围岩控制机理研究及应用[J]. 岩石力学与工程学报, 2005, 24(12): 2107–2112.
HUA Xinzhu, MA Junfeng, XU Tingjiao. Study on controlling mechanism of surrounding rocks of gob-side entry with combination of roadside reinforced cable supporting and roadway bolt supporting, and its application[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(12): 2107–2112. DOI:10.3321/j.issn:1000-6915.2005.12.017 (in Chinese) |
| [17] |
阚甲广, 张农, 李宝玉, 等.
典型留巷顶板条件下巷旁充填体支护阻力分析[J]. 岩土力学, 2010, 29(10): 2778–2784.
KAN Jiaguang, ZHANG Nong, LI Dingyu, et al. Analysis of supporting resistance of backfilling wall for gob-side entry retaining under typical roof conditions[J]. Rock and Soil Mechanics, 2010, 29(10): 2778–2784. (in Chinese) |
| [18] |
文志杰, 蒋宇静, 宋振骐, 等.
沿空留巷围岩结构灾变系统及控制力学模型研究[J]. 湖南科技大学学报:自然科学版, 2011, 26(3): 12–16.
WEN Zhijie, JIANG Yujing, SONG Zhenqi, et al. Study on mechanical model and surrounding rock catastrophe system of Gob-side retaining entry[J]. Journal of Hunan University of Science & Technology:Natural Science Edition, 2011, 26(3): 12–16. (in Chinese) |
| [19] | Whittaker B N, Woodrow G J M. Design loads for gateside packs and support systems[J]. Mining Engineering, 1977, 189(136): 263–275. |
| [20] | Smart. B. G. D, Davies. D. O etc. Application of the rock-title approach to pack design in an arch-sharped roadway[J]. Mining Engineer, Dec, 1982. |
| [21] | 曹胜根. 采场围岩整体力学模型及应用研究[D]. 徐州: 中国矿业大学, 1999. |
| [22] | 钱鸣高, 刘听成. 矿山压力及其控制[M]. 北京: 煤炭工业出版社, 1991. |
 2013, Vol. 36
2013, Vol. 36

