2. 华北电力大学 电气与电子工程学院, 北京 102206
2. School of Electrical and Electronic Engineering, North China Power University, Beijing 102206, China
全封闭气体绝缘组合电器(gas insulated switchgear,GIS)是由各种电气元器件、SF6管道气室以及SF6绝缘气体介质等组成的全封闭系统,其内部的良好绝缘状态是保证设备安全运行的必要条件。然而,由于GIS腔体结构的独特性和内部机构的复杂性,加上检修时的疏忽,GIS内部不可避免地会存在各种绝缘缺陷(如微量铁屑、盆式绝缘子表面上金属污染、金属突出物等),在运行中这些绝缘缺陷会不断加剧,最终必然会导致在GIS内部不同位置产生局部放电(partial discharge,PD)。PD是设备内部绝缘击穿前的征兆和主要表现形式,又是促使绝缘进一步劣化的主要原因[1]。PD类型本身的多态性[2]以及PD产生的随机性与分散性,使实际GIS内可能因多绝缘缺陷同时存在而诱发多PD。
多PD源所激发的超高频(ultra high frequency,UHF)电磁波信号在类似同轴波导[3]的GIS腔体内传播时,其空间介质的不均匀性会导致电磁波的传播发生衰减、反射、谐振[4]和色散等,使多PD信号在GIS腔体内出现传播延迟和相互干扰的混叠状况,而外置UHF传感器检测到的PD信号则是一个多PD源产生的混合信号。迄今为止,UHF PD信号的检测与分析已经成为在线评估GIS设备内部绝缘缺陷的有效方法[5-6]。然而,现有方法都是针对GIS内单一绝缘缺陷产生PD信号的假设,却忽视了GIS内部可能同时存在多绝缘缺陷的情形,至今尚无对GIS内多绝缘缺陷产生多PD信号的分析研究报道。
对多PD源产生多PD信号的分离方法有瞬时混合分离和卷积混合分离。瞬时混合分离方法能够实现分离对脉冲类模拟多PD信号的分离[7],但是瞬时混合分离方法忽略了信号传播过程中的延迟问题,分离出的信号无法真正反映原始PD信号波形。为了对GIS内多绝缘缺陷同时产生的多PD信号进行深入研究,实现信号混合模型与真实物理模型的无限逼近,在充分考虑PD信号传播延迟的基础上,建立卷积混合模型以描述GIS内PD信号的混合过程,并结合PD信号的非平稳特征构建分离算法,对多PD信号实现分离以获取单一PD信号,为后续有效辨识GIS内各绝缘缺陷类型奠定基础。
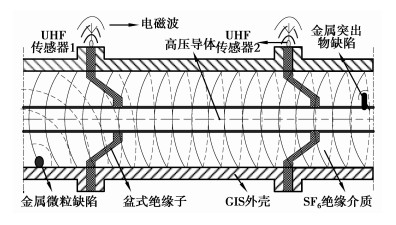
1 多PD信号特征为了获得GIS内多绝缘缺陷对应的表征各绝缘缺陷类型的单一PD信号,必须对UHF多PD信号的混合过程进行深入分析,才能找到合适的分离算法以实现对多PD信号的有效分离。GIS内2种绝缘缺陷(金属微粒和金属突出物缺陷)产生的2个PD源信号在传播与混合过程以及外置UHF传感器获取多PD信号如图 1。
|
图 1 GIS内多PD传播与混合示意图 |
一方面,GIS内单一绝缘缺陷产生的UHF PD电磁波在沿近似同轴波导的GIS腔体传播过程中,GIS腔体空内的盆式绝缘子、弯角部件以及交叉接头等电气元件与SF6绝缘气体构成不均匀的传播介质,使电磁波在GIS腔体内会发生反射、色散和透射的物理传播过程,从而引起电磁波能量衰减,并使PD特征波形具有较长的衰减时间。另一方面,当PD信号电磁波沿着同轴波导方向传播到GIS腔体尽头并发生多次反射时,反射回来的电磁波再次被同一UHF传感器检测,此时在PD信号波形上表现为滞后于PD特征波形的振荡信号,反射波的能量相对于PD特征波形而言,衰减较大。因此,PD信号波形为表征绝缘缺陷类型的特征波形和反映电磁波传播距离的反射波形的混合叠加。PD信号的传播物理过程使得其能量在传播通道上逐渐衰减,因而在实际的GIS外置传感器检测发生PD的距离是有限的。
在不同位置的绝缘缺陷同一时刻产生的多PD信号,距离同一传感器位置较近的PD源能量要远远大于较远的,任何PD信号波形主要反映就近绝缘缺陷产生的PD信号。因此,对某一传感器而言,其他较远PD信号可视为干扰加以消除,即只保留主要信号。同时,对于GIS内多绝缘缺陷产生的多PD信号在GIS腔体内同向或异向传播时,既具有上述单一PD信号的幅值衰减与混合过程,也具有不同PD信号的相对传播时延过程,使检测到的外置UHF PD信号并非是几个PD信号的简单线性叠加,而是具有相对传播时延、幅值衰减以及相互干扰等更为复杂的混合过程。
针对GIS内多PD信号传播必然产生的信号幅值衰减及传播时延,为了更能准确揭示GIS内PD信号的复杂混合过程以及多PD信号的有效分离,笔者采用信号卷积理论[8]建立GIS内PD信号的复杂混合过程模型,从构建多信号的卷积混合模型入手,研究GIS内多PD信号的混合与分离。
2 PD信号卷积混合模型为不失一般性,假定GIS内有n个绝缘缺陷,同时产生n个PD信号的电磁波在GIS腔体内传播与混合,在GIS外壳的盆式绝缘子上安放有m个UHF外置传感器检测其多PD信号。任意一个UHF传感器所检测到的多PD信号的时域模型可表示为
| $ {{x}_{j}}\left( t \right)=\sum\limits_{i=1}^{n}{\sum\limits_{k=0}^{L}{{{h}_{ji}}\left( k \right){{s}_{i}}\left( t-k \right)}}, $ | (1) |
式中:xj(t)为第j个传感器在t时刻检测到的多PD信号;si为第i个在t时刻统计上相互独立的PD信号;hij(k)为第i个信号源到第j个传感器的时延为k的FIR滤波器系数;L为FIR阶数。对于所有的PD信号和UHF多PD信号,GIS内多PD信号的线性瞬时卷积混合过程,可用滤波器矩阵H来表达
| $ {{\mathit{\boldsymbol{H}}}_{k}}={{\left[\begin{matrix} {{h}_{11}} & \cdots & {{h}_{1n}} \\ \vdots & {} & \vdots \\ {{h}_{m1}} & \cdots & {{h}_{mm}} \\ \end{matrix} \right]}_{m\times n}}, $ | (2) |
设S(t)=[s1(t),s2(t),s3(t),…,sn(t)]T为PD信号矢量,X(t)=[x1(t),x2(t),x3(t),…,xn(t)]T为检测到的多PD信号矢量,则外置UHF传感器检测多PD信号的矩阵混合模型为
| $ \mathit{\boldsymbol{X}}\left( t \right)=\sum\limits_{k=0}^{L}{{{\mathit{\boldsymbol{H}}}_{k}}\mathit{\boldsymbol{S}}\left( t-k \right)}。$ | (3) |
对平稳信号而言,常用的有效分析方法是频域法,然而实测信号多数具有非平稳特性[9]。文献[10]对非平稳卷积混合信号进行了分离研究,源信号应满足假设:①在短时间内信号是平稳的;②在长时间内信号必定是非平稳的。
依据假设①,可将检测到的非平稳信号X(t)划分为短时ts内平稳的子信号X(ts),在短时间内对平稳子信号X(ts)作短时Fourier变换(SFT),记为X(ω,ts),则与源信号S(t)SFT变换S(ω,ts)之间的关系为
| $ \mathit{\boldsymbol{X}}\left( \omega, {{t}_\text{s}} \right)=\mathit{\boldsymbol{H}}\left( \omega \right)\mathit{\boldsymbol{S}}\left( \omega, {{t}_\text{s}} \right), $ | (4) |
式中,H(ω)为卷积算子的SFT变换。
设频率ω固定不变,将X(ω,ts)作为平稳信号,即为固定频率的时间序列,记为
| $ {{\mathit{\boldsymbol{X}}}_{\omega }}\left( {{t}_\text{s}} \right)=\mathit{\boldsymbol{X}}\left( \omega, {{t}_\text{s}} \right)。$ | (5) |
采用Molgedey-Schuster解相关算法[11]对式(5)进行分离。值得注意得是Xω(ts)为复数,故必须采用Hermite矩阵和酉(矩)阵分别代替Molgedey-Schuster解相关法中的对称矩阵和正交矩阵进行计算。
对所有划分时间段内同样采用上述方法,就可以得到频率固定且分量相互独立的估计信号矢量
| $ {\widehat{\mathit{\boldsymbol{U}}}}_{\omega }\left( {{t}_\text{s}} \right)=\widehat{\mathit{\boldsymbol{B}}}\left( \omega \right){{\mathit{\boldsymbol{X}}}_{\omega }}\left( {{t}_\text{s}} \right), $ | (6) |
式中,
为了解决幅值的不确定性问题,Noboru Murata等[9]进行了深入研究,可以通过下列频谱分解得到第i个独立分量幅值
| $ \widehat{v}\left( {{t}_\text{s}};i \right)=\mathit{\boldsymbol{B}}{{\left( \omega \right)}^{-1}}{{\left[0\ \cdots \ {{\widehat{u}}_{i, w}}\left( {{t}_\text{s}} \right)\ \cdots \ 0 \right]}^{\text{T}}}, $ | (7) |
式中:i指估计
由于分离算法导致的幅值不确定性,信号重建时必须采取置换手段以实现不同频率间信号的无缝连接。对于平稳信号,不同频率的Fourier变换(FT)包络线之间是不相关的,而对于非平稳信号,来自同一源信号不同频率子信号FT变换包络线之间具有相关性:因此,可以采用信号包络线之间的相关性对分离的独立分量进行信号重构。
首先定义滑动平均算子ε为
| $ {{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( {{t}_\text{s}};i \right)}}=\frac{1}{2m}\sum\limits_{t{{'}_{s}}={{t}_\text{s}}-m}^{{{t}_\text{s}}+m}{\sum\limits_{j=1}^{n}{\left| {{v}_{j, \omega }}\left( {{t}_\text{s}}';i \right) \right|}}, $ | (8) |
式中:m是一个正常数,vj,ω(ts;i)是
| $ \left. \begin{align} &{{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( i \right)}}\cdot {{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( j \right)}}=\sum\limits_{{{t}_\text{s}}}{{{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( {{t}_\text{s}};i \right)}}\cdot {{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}'\left( {{t}_\text{s}};j \right)}}} \\ &\ \ \ \left\| {{\varepsilon }_{{{v}_{_{\omega }}}\left( i \right)}} \right\|=\sqrt{{{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( i \right)}}\cdot {{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( i \right)}}} \\ \end{align} \right\}。$ | (9) |
频域分离子PD信号重构的具体步骤如下
1) 采用独立分量之间的弱相关对频率ω排序,实现如下
| $ \text{sim}\left( \omega \right)=\sum\limits_{i\ne j}{\frac{{{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( i \right)}}\cdot {{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( j \right)}}}{\left\| {{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( i \right)}} \right\|\left\| {{\varepsilon }_{{{\widehat{v}}_{_{\omega }}}\left( j \right)}} \right\|}}, $ | (10) |
| $ \text{sim}\left( {{\omega }_{1}} \right)\leqslant \text{sim}\left( {{\omega }_{2}} \right)\leqslant \cdots \leqslant \text{sim}\left( {{\omega }_{3}} \right)。$ | (11) |
2) 对于ω1,赋值
| $ {{\widehat{y}}_{{{\omega }_{1}}}}\left( {{t}_\text{s}};i \right)={{\widehat{v}}_{{{\omega }_{1}}}}\left( {{t}_\text{s}};i \right), \left( i=1, 2, 3, \cdots n \right)。$ | (12) |
3) 对于ωk,寻找置换σ(i),使得ωk的包络线与从ω1至ωk-1的包络线之间的最大相关性ηmax,即
| $ {{\eta }_{\max }}=\max \left\{ \sum\limits_{i=1}^{n}{{{\varepsilon }_{{{\widehat{v}}_{_{{{\omega }_{k}}}}}\left( \delta \left( i \right) \right)}}}\cdot \left( \sum\limits_{j=1}^{k-1}{{{\varepsilon }_{{{\widehat{y}}_{_{{{\omega }_{j}}}}}\left( i \right)}}} \right) \right\}。$ | (13) |
然后赋值
| $ {{\widehat{y}}_{_{{{\omega }_{k}}}}}\left( {{t}_\text{s}};i \right)={{\widehat{v}}_{_{{{\omega }_{k}}}}}\left( {{t}_\text{s}};\delta \left( i \right) \right), $ | (14) |
式中σ(i)表示i为1~n的所有可能置换。对所有的频率,重复该步骤,这样就解决了信号重构时的不确定性,得到分离置换后的源信号频谱估计
| $ \widehat{y}\left( \omega, {{t}_\text{s}};i \right)={{\widehat{y}}_{\omega }}\left( {{t}_\text{s}};i \right)。$ | (15) |
对式(15)作IFT变换就能得到各分离的源信号
| $ y\left( t;i \right)=\frac{1}{2\pi W\left( t \right)}\sum\limits_{{{t}_\text{s}}}{\sum\limits_{\omega }{\widehat{y}\left( \omega, {{t}_\text{s}};i \right){{\text{e}}^{j\omega \left( t-{{t}_\text{s}} \right)}}}}, $ | (16) |
式中:W(t)=
分离效果的评价是混合信号分离的必要环节,评价指标是对分离算法分离效果客观评价的依据,本文采用评价指标信号干扰比(SIR)和波形相似系数(λ)对分离效果进行评价。
1) 信号干扰比
信号干扰比(signal interference ratio,SIR)用来衡量混合信号和分离信号相对于源信号的受干扰程度,通过SIR的增幅来评价分离效果。SIR定义为
| $ \text{SIR}=-10\ \lg \left( \frac{\left\| x_i-s_j \right\|_{2}^{2}}{\left\| {{s}_{j}} \right\|_{2}^{2}} \right), $ | (17) |
式中,在计算混合信号对于源信号的SIR (SIRxs)时,xi表示混合信号,而在计算分离信号对于源信号的SIR(SIRys)时,xi表示分离信号,i和j分别为相似波形分别对应的信号,则信号干扰比增幅ΔSIR为
| $ \Delta \text{SIR}=\text{SI}{{\text{R}}_{\text{xs}}}-\text{SI}{{\text{R}}_{\text{ys}}}Z, $ | (18) |
ΔSIR越大说明信号间的相互干扰越小。
2) 波形相似系数
波形相似系数[12]反应了分离信号相对源信号波形畸变的程度,定义为
| $ \lambda \left( {{y}_{i}}, {{s}_{j}} \right)=\frac{\sum\limits_{k=1}^{M}{\left| {{y}_{i}}\left( k \right){{s}_{j}}\left( k \right) \right|}}{\sqrt{\sum\limits_{k=1}^{M}{y_{_{i}}^{2}\left( k \right)s_{_{j}}^{2}\left( k \right)}}}, $ | (19) |
式中0 < λij≤1,i,j=1,2,…,N分别为原信号数和分离信号对应的比较信号,λ越大,波形越相似,说明分离效果越好。
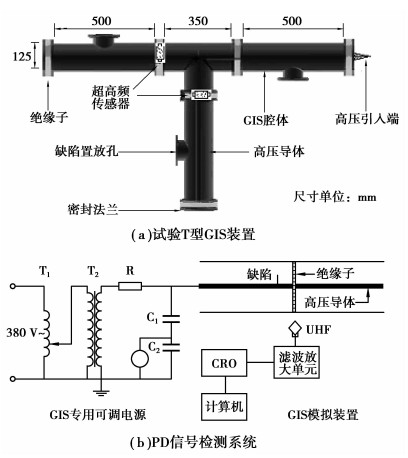
5 实测多PD信号分离在实验室GIS模拟研究平台上,首先对构建的4种典型绝缘缺陷分别单独产生的PD实验,然后将4种典型绝缘缺陷分别两两组合后再进行多绝缘缺陷的PD实验,采用外置UHF传感器检测其PD信号,对多PD信号进行分离,并将分离信号与单一PD检测信号进行对比分析,以证实对GIS内多PD信号线性卷积混合过程假设的正确性以及提出分离算法的有效性。GIS模拟装置与PD实验接线如图 2所示。
|
图 2 GIS试验装置与PD信号检测 T1:感应调压器;T2:无局放试验变压器;C1/C2:电容分压器;R:保护电阻;CRO:高速超大容量数字存储示波器;UHF:超高频传感器. |
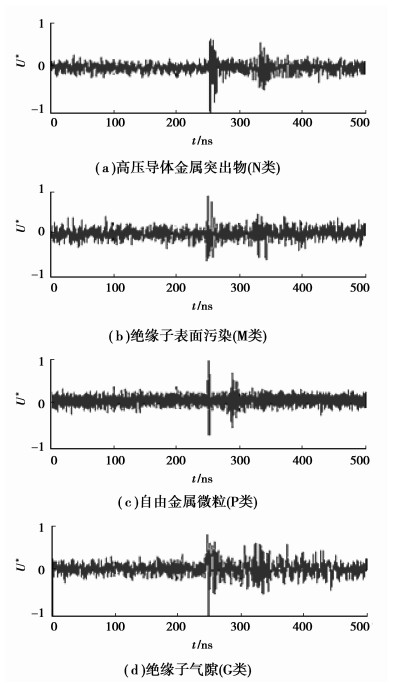
用构造的高压导体金属突出物(简称N类缺陷)、绝缘子污染(简称M类缺陷)、自由金属微粒(简称P类缺陷)和绝缘子气隙(简称G类缺陷)四种典型绝缘缺陷物理模型[13]分别置于GIS内,外施电压直至各绝缘缺陷产生稳定的PD,采用安装在支撑绝缘子外侧的UHF天线传感器[14-15]检测各PD信号,分别测得PD信号的时域波形如图 3。
|
图 3 实测UHF PD信号 |
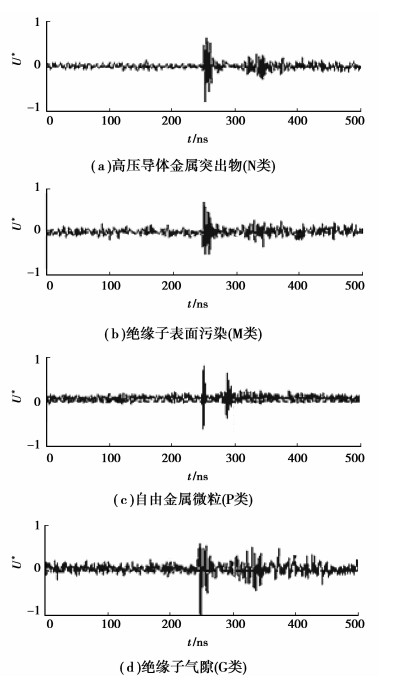
由图 3所示的4个PD信号发现测量噪声对信号有一定程度的污染。显然,在PD信号特征波及反射波的无信号区域,噪声污染很重且幅值较大,可以推知,在PD信号的信号区域,同样包含严重的噪声信号。为了便于清晰观察各绝缘缺陷对应的PD信号特征波形,采用小波变换去噪,尽可能减小噪声对信号的干扰而还原各真实的PD信号,去噪后的PD信号如图 4。为定量评价去噪前后各PD信号的干扰程度,分别对去噪前后各PD信号的信噪比(SNR)进行估计[16],如表 1。
|
图 4 去噪后的PD信号 |
| 表 1 各PD信号去噪前后的SNR比较 |
比较表 1去噪前后估计的SNR值,很显然,去噪后各PD信号的SNR值大幅度提高,均在20 dB以上,充分说明噪声对各PD信号的干扰已经很小。从理论上讲,任何去噪法都不可能完全消除噪声干扰而还原其真实信号,因此,笔者把去噪后得到的各PD信号(图 4)视为单一绝缘缺陷产生的真实PD信号,以便与后面多绝缘缺陷产生多PD信号分离后比较。目测图 4的各去噪PD信号,相对图 3而言,噪声干扰大幅度减小,各PD信号脉冲的特征波形突显可辨,不同绝缘缺陷对应的PD波形特征各不相同;同时,在PD信号特征波形后,存在信号能量相对较小的反射波,其原因是PD信号在GIS内传播过程中遇到GIS管壁而产生反射形成。可以看出,由于产生反射波的GIS空间环境不同其波形亦不相同。
由于UHF PD信号特性与其检测传感器密切相关,为了掌握各实测PD信号的特性,采用快速傅立叶变换(FFT)对各PD信号进行频谱分析。以图 3(a)高压导体金属突出物产生的PD信号为例,其频谱如图 5所示。观察可知,信号能量主要集中在300 MHz左右的范围内,也有部分信号能量分布在200 MHz以下和1 GHz左右。结合信号分析,PD信号特征波形对应的频率应在300 MHz左右的范围内,其余频率反映的是PD反射波和信号噪声的能量。这是因为从特征波和反射波本身在GIS内部形成的机理推断,特征波能量幅值较大、频率范围较窄,而反射波和噪声能量幅值应相对较小、频率范围较宽。从图 5反映的信号能量频率范围推知,该UHF传感器具有较好的低频干扰抑制性能。图 5的频谱基本上能体现4个PD信号的频率分布范围,当然各PD信号具体的频谱不同。观察图 5的PD频谱,可知PD信号具有非平稳特性[17],这也是外置UHF PD信号的显著特征,其余信号同样具有此非平稳特性,鉴于篇幅所限就不再详述了。
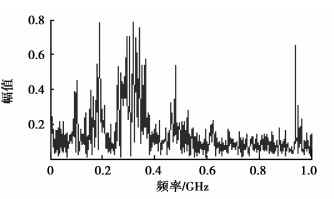
|
图 5 N缺陷的PD源信号频谱 |
对上述4种典型绝缘缺陷进行两两组合可至少形成4组多绝缘缺陷物理模型,即①N类和M类;②P类和G类;③N类和P类;④M类和G类。分别在图 2所示的实验研究平台上进行两两组合绝缘缺陷试验,当外施电压一定时,2种绝缘缺陷会同时产生稳定的PD,用性能相同的2个UHF天线传感器检测其多PD信号。为了节省篇幅,以P和G组合绝缘缺陷为例,实测得到的多PD信号如图 6。
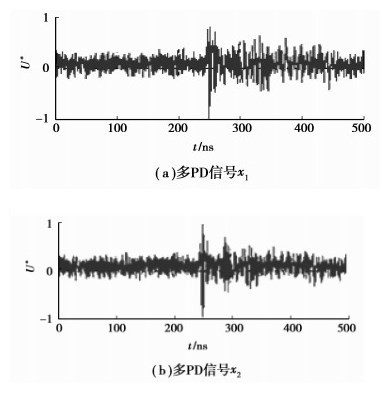
|
图 6 实测多PD信号 |
观测图 6中的实测多PD信号,干扰比较严重,同样对这组多PD信号采用小波去噪,以减小噪声干扰对分离性能的影响,去噪后的多PD信号如图 7所示。对各组多PD信号去噪前后的SNR(去噪前SNR1,去噪后SNR2)进行估计,以便对干扰程度做定量评价,见表 2所示。从去噪波形以及SNR计算结果看出,多PD信号的噪声干扰程度下降较大,把去噪后的多PD信号(图 7)作为被分离的原多PD信号。
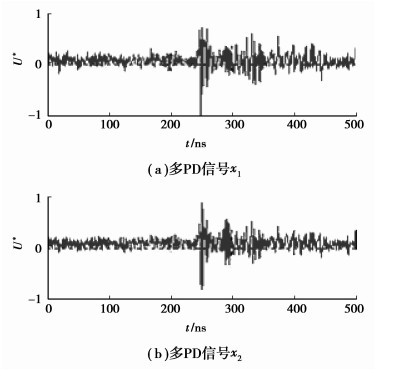
|
图 7 去噪的多PD信号 |
| 表 2 各组多PD信号去噪前后的SIR比较 |
比较图 7的多PD信号波形与图 4中单一PD信号波形(a)和(b),多PD信号的特征波形和反射波形差异比较大,因此,实测多PD信号不能直接作为GIS内绝缘缺陷类型判别的依据。如果盲目地采用这样的多PD信号进行绝缘缺陷类型的判别与分析,必然得出错误的结论。为此,必须对混合信号进行分离,还原其单一的PD信号,才能为后续的故障辨识提供可靠的信息。
5.3 实测多PD信号的分离根据前面对单一PD信号的分析以及UHF PD信号的特征,实测多PD信号仍然是非平稳信号,该信号自然满足前述分离算法的假设②。只要对PD信号作适当分段处理,划分为短时(弱)平稳信号,就能满足假设①。这样实测多PD信号就可以采用本文提出的卷积分离算法进行分离,以获取单一PD信号。对组合②(P类和G类)得到混合信号进行分离,其分离后信号如图 8所示,对分离的PD信号采用波形相似系数λ、信号干扰比SIR和ΔSIR进行分离效果的定量评价,表 3是4组绝缘缺陷产生混合信号分离后的评价数据(这里省略了3组绝缘缺陷产生混合信号的分离波形图)。
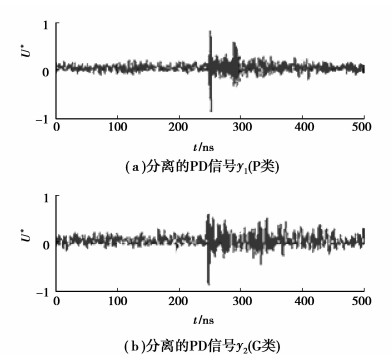
|
图 8 分离的PD信号 |
| 表 3 各组多PD信号分离效果评价 |
由表 3可知,分离所得的PD信号与图 4中的PD信号在各绝缘缺陷组合中对应的相似系数都比较大,其中组合①中PD信号(b)的相似系数达到了0.91,最小的相似系数(组合③)也达到了0.76,多数在0.8以上。部分系数较小的原因在于信号中的噪声干扰所致。因此,对实测UHF多PD信号,分离前在保持原有信号波形特征的前提下,信号去噪效果对分离性能有一定的影响。观察信号干扰比SIR,未分离的多PD信号相对于去噪后的PD信号,其信号干扰比(SIRxs)都很小,均在1 dB以下,说明多PD后中各信号间的相互干扰比较大。相对于SIRxs,在不同组合中对应的分离后的信号干扰比(SIRys)则有不同幅度的提高,最高到达7.42 dB,最小也在4 dB以上,说明多PD信号发生了分离,各组合中PD信号之间的相互干扰大幅度降低。观测图 8和表 3中的分离效果评价指标,表明对去噪后实测PD混信号的分离是成功的。
上述多PD信号分离是针对GIS内绝缘缺陷个数与外部检测传感器个数相等的情形,即两绝缘缺陷和两检测传感器。然而,由于GIS内绝缘缺陷故障产生的随机性,在已知外部安装检测传感器个数的前提下,内部绝缘缺陷个数可能少于或多于传感器个数的各种情形都有可能存在,对这类多绝缘缺陷情形,还有待于继续专题研究。
6 结论1) 针对GIS内可能同时存在多绝缘缺陷从而导致GIS内潜在绝缘故障类型辨识难的问题,提出对外置UHF传感器获取的多PD信号进行分离的新思路,以获取表征各绝缘缺陷类型的单一PD信号,并建立了分离效果的评价指标,为多绝缘缺陷类型的辨识奠定了基础。
2) 分析了PD信号电磁波在GIS腔体内的传播与混合机理,针对多PD信号在GIS腔体中的复杂混合过程,提出采用卷积混合模型对多PD信号在GIS的混合过程进行定性描述,并用仿真和实测多PD信号的有效分离予以了证实。
3) 分析了PD信号的特征,针对多PD信号的非平稳特性,提出将多PD信号在时域空间下划分为短时平稳PD信号子集合,并在频域空间下进行分离,再通过信号包络线的相关性进行信号重构,从而解决了用外置UHF传感器检测的多绝缘缺陷诱发多PD信号辨识难的问题。
| [1] | Hasegawa Y, Lzumi K, Kobayashi A, et al. Investigation on phenomena caused by insulation abnormalities in actual GIS[J]. IEEE Transactions on Power Delivery, 1994, 9(2): 796–804. DOI:10.1109/61.296259 |
| [2] |
钱勇, 黄成军, 陈陈, 等.
多小波消噪算法在局部放电检测中的应用[J]. 中国电机工程学报, 2007, 27(6): 89–94.
QIAN Yong, HUANG Chengjun, CHEN Chen, et al. Application of multi-wavelet based on denoising algorithm in partial discharge detection[J]. Proceedings of the CSEE, 2007, 27(6): 89–94. (in Chinese) |
| [3] |
张鸣超, 王建生, 邱毓昌.
GIS中局部放电产生的超高频电磁波及其测量[J]. 高电压技术, 1998, 24(2): 22–25.
ZHANG Mingchao, WANG Jiansheng, QIU Yuchang. UHF electromagnetic waves excited by partial discharge in GIS and their measurements[J]. High Voltage Engineering, 1998, 24(2): 22–25. (in Chinese) |
| [4] |
黄兴泉, 康书英, 李泓志, 等.
Gis局部放电超高频电磁波的传播特性研究[J]. 高电压技术, 2006, 32(10): 32–35.
HUANG Xingquan, KANG Shuying, LI Hongzhi, et al. Simulation study on the characteristic of ultra-high frequncy electromagnetic wave in GIS[J]. High Voltage Engineering, 2006, 32(10): 32–35. DOI:10.3969/j.issn.1003-6520.2006.10.010 (in Chinese) |
| [5] |
王建生, 邱毓昌.
气体绝缘开关设备中局部放电的在线监测技术[J]. 电工电能新技术, 2000, 19(4): 44–48.
WANG Jiansheng, QIU Yuchang. On-line partial discharge monitoring techniques for gas insulated substations[J]. Advanced Technology of Electrical Engineering and Energy, 2000, 19(4): 44–48. (in Chinese) |
| [6] |
金立军, 刘卫东, 钱家骊.
GIS绝缘配合中的故障分析及诊断和检测技术[J]. 中国电力, 2002, 35(2): 52–55.
JIN Lijun, LIU Weidong, QIAN Jiali. The failure analysis and diagnostic and detection technology of insulation coordination in GISJIN[J]. Electric Power, 2002, 35(2): 52–55. (in Chinese) |
| [7] | Tang J, Li W, Liu Y L. Blind source separation of mixed PD signals produced by multiple insulation defects in GIS[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 170–176. DOI:10.1109/TPWRD.2009.2035296 |
| [8] |
楼红伟, 胡光锐.
基于小波域的非平稳卷积混合语音信号的自适应盲分离[J]. 控制与决策, 2004, 19(1): 73–76.
LOU Hongwei, HU Guangrei. Adaptive wavelet domain algorithm for blind separation of non-stationary convolved speech mixtures[J]. Control and Decision, 2004, 19(1): 73–76. (in Chinese) |
| [9] |
冯志鹏, 李学军, 褚福磊.
基于平稳小波包分解的水轮机非平稳振动信号希尔伯特谱分析[J]. 中国电机工程学报, 2006, 26(12): 79–84.
FENG Zhipeng, LI Xuejun, CHU Fulei. Application of stationary wavelet packets decomposition based Hilbert spectrum to nonstationary hydraulic turbine vibration signal analysis[J]. Proceedings of the CSEE, 2006, 26(12): 79–84. DOI:10.3321/j.issn:0258-8013.2006.12.014 (in Chinese) |
| [10] | Murata N, Ikeda S, Ziehe A. An approach to blind source separation based on temporal structure of speech signals[J]. Neurocomputing, 2001, 41(1/2/3/4): 1–24. |
| [11] | Molgedey L, Schuster H G. Separation of a mixture of independent signals using time delayed correlations[J]. Physical Review Letters, 1994, 72(23): 3634–3637. DOI:10.1103/PhysRevLett.72.3634 |
| [12] |
唐炬, 彭莉, 谢颜斌.
一种用于抑制白噪声的分层复阈值算法[J]. 中国电机工程学报, 2007, 27(21): 25–30.
TANG Ju, PENG Li, XIE Yanbin. An algorithm of complex multilevel threshold for reducing white-noise[J]. Proceedings of the CSEE, 2007, 27(21): 25–30. DOI:10.3321/j.issn:0258-8013.2007.21.005 (in Chinese) |
| [13] | Tang J, Zhou Q, Tang M, et al. Study on mathematical model for VHF partial discharge of typical insulated defects in GIS[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(1): 30–38. DOI:10.1109/TDEI.2007.302869 |
| [14] |
张晓星, 唐炬, 彭文雄, 等.
GIS局部放电检测的微带贴片天线研究[J]. 仪器仪表学报, 2006, 27(12): 1595–1599.
ZHANG Xiaoxing, TANG Ju, PENG Wenxiong, et al. Study on the outer UHF microstrip patch antenna forpartial discharge detection in GIS[J]. Chinese Journal of Scientific Instrument, 2006, 27(12): 1595–1599. (in Chinese) |
| [15] |
唐炬, 魏钢, 孙才新, 等.
GIS局部放电检测用超宽频带振子天线传感器研究[J]. 高电压技术, 2004, 30(3): 29–31, 42.
TANG Ju, WEI Gang, SUN Caixin, et al. Research on the dipole antenna sensor with broadband for partial discharge detection in GIS[J]. High Voltage Engineering, 2004, 30(3): 29–31, 42. (in Chinese) |
| [16] |
范海波, 陈军, 曹志刚.
AWGN信道中非恒包络信号SNR估计算法[J]. 电子学报, 2002, 30(9): 1369–1371.
FAN Haibo, CHEN Jun, CAO Zhigang. An algorithm of SNR estimation for non-constant envelope signal in the AWGN channel[J]. Acta Electronica Sinica, 2002, 30(9): 1369–1371. (in Chinese) |
| [17] |
胡明友, 谢恒堃, 蒋雄伟, 等.
基于小波变换抑制局部放电监测中平稳性干扰的滤波器的研究[J]. 中国电机工程学报, 2000, 20(1): 37–40.
HU Mingyou, XIE Hengku, JIANG Xiongwei, et al. Study on WTST-NST filter used for suppression of stationary noises in PD monitoring[J]. Proceedings of the CSEE, 2000, 20(1): 37–40. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

