2. 西南交通大学, 成都 610031
2. Southwest Jiaotong University, Chengdu 610031, China
随着非线性、强耦合机器人对跟踪精度、稳定性、鲁棒性要求不断提高,机器人系统中的摩擦导致了关节的跟踪精度降低、黏滑运动以及极限环振荡加剧等问题,更严重的是当机器人低速重载运行时,摩擦甚至造成了50%的误差[1-3]。而缺乏死区补偿,将增大机器人控制力矩和摩擦力矩的误差,导致大幅振荡,影响系统的动态响应。同时,负载、润滑、环境的改变及传动机构的温度、磨损量的变化将分别导致摩擦及死区的变化。因此,进行机器人摩擦力和死区补偿是非常有必要的。国内外众多学者开展了大量关于机器人摩擦补偿方法的研究[2-4],但存在如下缺陷:1)补偿效果由离线参数估计决定;2)忽略了某些关键的摩擦特性;3)摩擦模型中只有部分参数有更新算子;4)把摩擦作为干扰,而未考虑摩擦的黏滑、stribeck效应等重要特性。同样,关于死区的补偿方法主要有:模糊逻辑、神经网络、线性矩阵不等式增益的保性能控制、重复学习控制等[5-8],这些方法同样存在不同程度的局限性,如文献[5-6]的神经网络补偿算法太过复杂,且不利于稳定性分析。文献[7]的算法收敛时间较长,而文献[8]所用算法的控制器增益较大。但很少有学者研究死区逆模型中期望力矩ud=0时其对应的带宽对机器人控制系统的影响。
具有并行计算推理、分布式信息存储和处理、自适应学习、强容错能力等众多优点的RBF神经网络,以及具有定性问题描述能力强、鲁棒性好、推理灵活等优点的模糊逻辑,特别适合于处理动态摩擦和死区这类不确定性、非线性问题,所以构造了基于两者结构等价的模糊RBF神经网络,用于机器人摩擦力矩补偿,以及设计了模糊逻辑系统,用于死区补偿[9]。此时,模糊神经网络的结构和权值都被赋予特定的物理含义,并可以基于先验知识及针对不同复杂程度的问题等设计出合适的模型。这样,就提高了机器人的学习速率、并实现了全局优化。
根据摩擦学的3个公理[10]和7种重要典型摩擦模型[2-3, 11-15]及非对称非线性死区的特性,在对大量的摩擦和死区补偿方法比较后,同时结合机器人的动力学模型,提出了一种智能补偿机器人系统中的摩擦和死区不确定性的滑模控制算法,达到了机器人高精度、高可靠的控制要求,仿真结果表明该方法是有效的。
1 考虑动态摩擦和死区补偿的机械臂动力学模型及其控制结构根据拉格朗日运动学,对自由度机器人建模为
| $ \mathit{\boldsymbol{D}}\left( q \right)\ddot q + \mathit{\boldsymbol{C}}\left( {q,\dot q} \right)\dot q + \mathit{\boldsymbol{G}}\left( q \right) + \mathit{\boldsymbol{F}}\left( {z,hz,\dot q} \right) + {\mathit{\boldsymbol{\tau }}_d} = \mathit{\boldsymbol{\tau }}, $ | (1) |
式中,q、
|
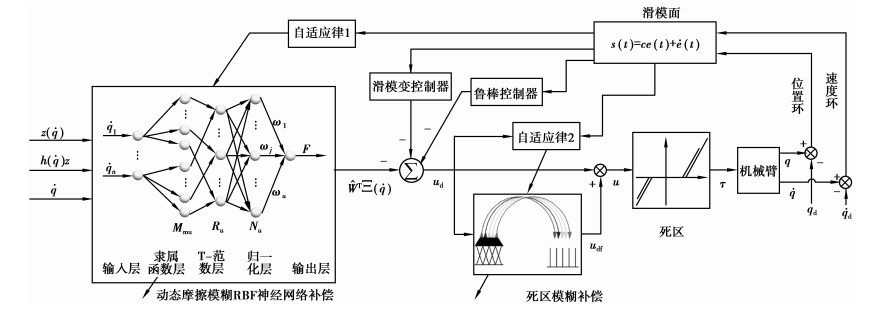
图 1 模糊RBF神经网络摩擦补偿和死区模糊补偿的机器人滑模变控制框架 |
机器人控制系统主要包括摩擦模糊神经网络整体补偿器、死区模糊补偿器、滑模控制器和鲁棒控制器。整个控制器的输入信号包括各关节的给定位置、速度、加速度,反馈信号包括各关节的位置和速度误差,输出信号包括绝对各关节的力矩、光栅编码器的实际位置及速度,构成位置和速度2个闭环,达到机器人高精度、高可靠智能控制的目的。
在图 1中,机械臂的未知干扰鲁棒项,τd=Kssat(s),Ksi=diag(ksi),Ksi>0,i=1,2,…,n,取δ>0,则饱和函数设计为
| $ {\rm{sat}}\left( s \right) = \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;s > \delta ;\\ s/\delta \;\;\;\left| s \right| \leqslant \delta ;\\ - 1\;\;\;\;\;\;s < - \delta 。\end{array} \right. $ | (2) |
在机器人动力学模型式(1)中,F为非线性动态摩擦项。根据文献分析可知,LuGre模型是一个能对摩擦的各种重要特性进行准确描述的摩擦模型。虽然有学者通过实验手段获得了LuGre模型的参数[3, 16],但其动态参数的准确辨识到目前为止仍然是一个难题。因此,文中在前期LuGre摩擦参数实验方法辨识的研究基础之上[3],开展了用模糊RBF神经网络来逼近其动态参数(由实验获得)的研究。
而LuGre摩擦模型是根据鬃毛的平均变形,即zi(关节i=1,2,…,n)的微分来描述[2-3, 17],表示为
| $ \frac{{{\rm{d}}{z_i}}}{{{\rm{d}}t}} = {{\dot q}_i} - \frac{{{\sigma _{0i}}\left| {{{\dot q}_i}} \right|}}{{g\left( {{{\dot q}_i}} \right)}}{z_i}。$ | (3) |
摩擦力由鬃毛的挠曲产生,可以描述为
| $ {F_i} = {\sigma _{0i}}{z_i} + {\sigma _{1i}}{{\dot z}_i} + {\sigma _{2i}}{{\dot q}_i}, $ | (4) |
式中,σ0i、σ1i和σ2i分别是鬃毛的刚度、微观阻尼系数和黏性摩擦系数,Stribeck效应由函数g(
| $ g\left( {{{\dot q}_i}} \right) = {F_{{\rm{c}}i}} + \left( {{F_{{\rm{s}}i}} - {F_{{\rm{c}}i}}} \right){e^{ - {{\left( {{{\dot q}_i}/{{\dot q}_{\rm{s}}}} \right)}^2}}}, $ | (5) |
式中Fci、Fsi分别为关节的库仑摩擦和黏性摩擦。
根据式(3)、(4)、(5),可以得出
| $ F = {\sigma _{0i}}{z_i} - {\sigma _{3i}}{h_i}\left( {{{\dot q}_i}} \right){z_i} + {\sigma _{4i}}{{\dot q}_i}, $ | (6) |
式中σ3i=σ0iσ1i,σ4i=σ1i+σ2i,
在机械臂系统中,动态摩擦力矩F为未知,可采用模糊RBF神经网络对F进行建模并估计[3, 18],输入语言变量为z(
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}} = \mathit{\boldsymbol{\hat F}}\left( {z\left( {\dot q} \right),h\left( {\dot q} \right)z\left( {\dot q} \right),\dot q} \right) + {\mathit{\boldsymbol{E}}_1} = }\\ {{{\left\{ {\mathit{\boldsymbol{\hat W}}} \right\}}^{\rm{T}}} \cdot \left\{ {{\bf{\Xi }}\left( {\dot q} \right)} \right\} + {\mathit{\boldsymbol{E}}_1},} \end{array} $ | (7) |
式中,Ŵ、E1分别为模糊RBF神经网络权值W的估计值和整体逼近误差。
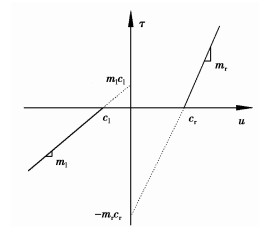
1.2 机械臂控制系统的非对称死区模糊补偿由图 2可知,机械臂非对称非线性死区可表示为
| $ \tau = D\left( u \right) = \left\{ \begin{array}{l} {m_1}u + {m_1}{c_1},u \leqslant - {c_1};\\ 0, - {c_1} \leqslant u \leqslant {c_{\rm{r}}};\\ {m_{\rm{r}}}u - {m_{\rm{r}}}{c_{\rm{r}}},u \geqslant {c_{\rm{r}}}。\end{array} \right. $ | (8) |
|
图 2 非对称非线性死区 |
式中,u、τ分别为进入死区前、后的控制力矩。ml、mr、cl、cr都为大于0的死区参数。
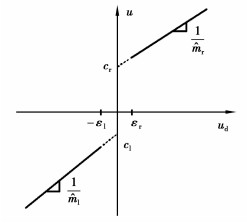
由图 3可知,死区的逆的估计为
| $ u = {D^{ - 1}}\left( {{u_{\rm{d}}}} \right) = \left\{ \begin{array}{l} \frac{{{u_{\rm{d}}} - {{\hat m}_1}{{\hat c}_1}}}{{{{\hat m}_1}}},{u_{\rm{d}}} \leqslant - {\varepsilon _1};\\ 0, - {\varepsilon _1} \leqslant {u_{\rm{d}}} \leqslant {\varepsilon _{\rm{r}}};\\ \frac{{{u_{\rm{d}}} - {{\hat m}_{\rm{r}}}{{\hat c}_{\rm{r}}}}}{{{{\hat m}_{\rm{r}}}}},{u_{\rm{d}}} \geqslant {\varepsilon _{\rm{r}}}。\end{array} \right. $ | (9) |
|
图 3 死区的逆的估计 |
式中,ud为机械臂系统的期望控制输入,
采用模糊补偿后的控制输入为
| $ u = {u_{\rm{d}}} + {u_{{\rm{d}}F}}。$ | (10) |
隶属函数设计为
| $ \left\{ \begin{array}{l} {X_{\rm{l}}}\left( {{u_{{\rm{d}}i}}} \right) = \left\{ \begin{array}{l} 0,{u_{{\rm{d}}i}} > - {\varepsilon _{\rm{l}}};\\ 1,{u_{{\rm{d}}i}}\leqslant - {\varepsilon _{\rm{l}}}; \end{array} \right.\\ {X_{\rm{r}}}\left( {{u_{{\rm{d}}i}}} \right) = \left\{ \begin{array}{l} 0,{u_{{\rm{d}}i}} < {\varepsilon _{\rm{r}}};\\ 1,{u_{{\rm{d}}i}} \geqslant {\varepsilon _{\rm{r}}}; \end{array} \right.\\ {X_{\rm{c}}}\left( {{u_{{\rm{d}}i}}} \right) = \left( {1 - {X_{\rm{l}}}} \right)\left( {1 - {X_{\rm{r}}}} \right) = \\ \left\{ \begin{array}{l} 0,{u_{{\rm{d}}i}}\leqslant - {\varepsilon _{\rm{l}}},{u_{{\rm{d}}i}} \geqslant {\varepsilon _{\rm{r}}};\\ 1, - {\varepsilon _{\rm{l}}} < {u_{{\rm{d}}i}} < {\varepsilon _{\rm{r}}}。\end{array} \right. \end{array} \right. $ | (11) |
根据反模糊化方法,并考虑到Xl+Xr+Xc=1,得模糊系统的输出为
| $ \begin{array}{*{20}{c}} {{u_{{\rm{d}}F}} = \left( {\frac{{{u_{\rm{d}}} - {{\hat m}_1}{{\hat c}_1}}}{{{{\hat m}_1}}} - {u_{\rm{d}}}} \right){X_{\rm{l}}}\left( {{u_{\rm{d}}}} \right) + }\\ {\left( {\frac{{{u_{\rm{d}}} + {{\hat m}_{\rm{r}}}{{\hat c}_{\rm{r}}}}}{{{{\hat m}_{\rm{r}}}}} - {u_{\rm{d}}}} \right){X_{\rm{r}}}\left( {{u_{\rm{d}}}} \right) - {\mathit{\boldsymbol{E}}_{\rm{d}}} + {\mathit{\boldsymbol{E}}_{{\rm{21}}}} + {\mathit{\boldsymbol{E}}_{{\rm{2r}}}},} \end{array} $ | (12) |
式中,Ed=εxXc,εx=ud(此时,|ud|≤max(εl,εr)),E2l,E2r为死区的模糊补偿估计误差。根据式(8)~(12),得死区后的控制输入为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{u}}_{\rm{d}}} + {{\left[ {{{\left\{ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}} \right\}}^{\rm{T}}}\left\{ {{{\mathit{\boldsymbol{\tilde W}}}_1}} \right\}} \right]}^{\rm{T}}}{X_{\rm{l}}} + {{\left[ {{{\left\{ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{r}}}} \right\}}^{\rm{T}}}\left\{ {{{\mathit{\boldsymbol{\tilde W}}}_{\rm{r}}}} \right\}} \right]}^{\rm{T}}}{X_{\rm{r}}} - }\\ {{\varepsilon _{\rm{x}}}{X_{\rm{c}}} + {\mathit{\boldsymbol{E}}_{2{\rm{l}}}} + {\mathit{\boldsymbol{E}}_{2{\rm{r}}}},} \end{array} $ | (13) |
| $ {\rm{其中}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}}=\left[ \begin{matrix} \frac{{{u}_{\rm{d1}}}-\overset\frown{{{m}_{\rm{l}1}}{{c}_{\rm{l}1}}}}{\overset\frown{{{m}_{\rm{l}1}}}}&\cdots &0 \\ 1&\cdots &0 \\ \vdots &{}&\vdots \\ 0&\cdots &\frac{{{u}_{\rm{d}n}}-\overset\frown{{{m}_{\rm{l}\mathit{n}}}{{c}_{\rm{l}\mathit{n}}}}}{\overset\frown{{{m}_{\rm{l}\mathit{n}}}}} \\ 0&\cdots &1 \\ \end{matrix} \right], $ |
| $ {{{\mathit{\boldsymbol{\tilde{W}}}}}_{\rm{l}}}=\left[ \begin{matrix} {{m}_{\rm{l1}}}-\overset\frown{{{m}_{\rm{l1}}}}&\cdots &0 \\ {{m}_{\rm{l1}}}-{{c}_{\rm{l1}}}-\overset\frown{{{m}_{\rm{l1}}}{{c}_{\rm{l1}}}}&{}&0 \\ \vdots &{}&\vdots \\ 0&\cdots &{{m}_{\rm{l}\mathit{n}}}-\overset\frown{{{m}_{\rm{l}\mathit{n}}}} \\ 0&\cdots &{{m}_{\rm{l}\mathit{n}}}{{c}_{\rm{l}\mathit{n}}}-\overset\frown{{{m}_{\rm{l}\mathit{n}}}{{c}_{\rm{l}\mathit{n}}}} \\ \end{matrix} \right], $ |
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{\rm{r}}}=\left[ \begin{matrix} \frac{{{u}_{\rm{d1}}}-\overset\frown{{{m}_{\rm{r}1}}{{c}_{\rm{r}1}}}}{\overset\frown{{{m}_{\rm{r}1}}}}&\cdots &0 \\ 1&\cdots &0 \\ \vdots &{}&\vdots \\ 0&\cdots &\frac{{{u}_{\rm{d}n}}-\overset\frown{{{m}_{\rm{r}\mathit{n}}}{{c}_{\rm{r}\mathit{n}}}}}{\overset\frown{{{m}_{\rm{r}\mathit{n}}}}} \\ 0&\cdots &1 \\ \end{matrix} \right], $ |
| $ {{{\mathit{\boldsymbol{\tilde{W}}}}}_{\rm{r}}}=\left[ \begin{matrix} {{m}_{\rm{r1}}}-\overset\frown{{{m}_{\rm{r1}}}}&\cdots &0 \\ {{m}_{\rm{r1}}}-{{c}_{\rm{r1}}}-\overset\frown{{{m}_{\rm{l1}}}{{c}_{\rm{l1}}}}&{}&0 \\ \vdots &{}&\vdots \\ 0&\cdots &{{m}_{\rm{r}\mathit{n}}}-\overset\frown{{{m}_{\rm{r}\mathit{n}}}} \\ 0&\cdots &{{m}_{\rm{r}\mathit{n}}}{{c}_{\rm{r}\mathit{n}}}-\overset\frown{{{m}_{\rm{r}\mathit{n}}}{{c}_{\rm{r}\mathit{n}}}} \\ \end{matrix} \right] $ |
为2n×n对角矩阵。
2 机械臂滑模变控制器的设计和稳定性分析 2.1 控制律的设计设理想的位置及实际的位置指令分别为qd,q,则跟踪误差定义为
| $ e = q - {q_{\rm{d}}}。$ | (14) |
滑模函数设计为
| $ s = {e_2} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{e_1}, $ | (15) |
其中Λ为正定矩阵,e2=ė,e1=-e。
定义
| $ {{\dot q}_{\rm{s}}} = {{\dot q}_{\rm{d}}} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}e。$ | (16) |
死区补偿前的理想控制律设计为
| $ \begin{array}{*{20}{c}} {{u_{\rm{d}}} = \mathit{\boldsymbol{D}}\left( q \right){{\ddot q}_{\rm{s}}} + \mathit{\boldsymbol{C}}\left( {q,\dot q} \right){{\dot q}_{\rm{s}}} + \mathit{\boldsymbol{G}}\left( q \right) + }\\ {\mathit{\boldsymbol{\hat F}}\left( {z,hz,\dot q} \right) - {\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{D}}}s,} \end{array} $ | (17) |
其中KD=diag(Ki),Ki>0。
自适应律设计为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot {\hat W}}}}_{{\rm{f}}i}} = - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{f}}i}} \cdot \left\{ {{\xi _{{\rm{f}}i}}\left( {z\left( {\dot q} \right),hz\left( {\dot q} \right),\dot q} \right)} \right\}{s_i}\left( k \right),\\ \;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\dot {\hat W}}}}_{{\rm{l}}i}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{l}}i}} \cdot \left\{ {{\varphi _{{\rm{l}}i}}} \right\}{X_{{\rm{l}}i}}{s_i}\left( k \right),\\ \;\;\;\;\;\;\;\;\;{{\mathit{\boldsymbol{\dot {\hat W}}}}_{{\rm{r}}i}} = {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{r}}i}} \cdot \left\{ {{\varphi _{{\rm{r}}i}}} \right\}{X_{{\rm{r}}i}}{s_i}\left( k \right), \end{array} $ | (18) |
其中Γfi-1,Γli-1,Γri-1为对称正定矩阵。
2.2 稳定性分析定义Lyapunov函数为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{V}} = \frac{1}{2}{s^{\rm{T}}}\mathit{\boldsymbol{D}}s + \frac{1}{2}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde W}}_{{\rm{f}}i}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{f}}i}^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{f}}i}}} + }\\ {\frac{1}{2}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde W}}_{{\rm{l}}i}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{l}}i}^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{l}}i}}} + \frac{1}{2}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde W}}_{{\rm{r}}i}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{r}}i}^{ - 1}{{\mathit{\boldsymbol{\tilde W}}}_{{\rm{r}}i}}} ,} \end{array} $ | (19) |
其中:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}} = {s^{\rm{T}}}\left[ {\mathit{\boldsymbol{D}}\dot s + \frac{1}{2}\mathit{\boldsymbol{\dot D}}s} \right] + \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde W}}_{{\rm{f}}i}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{f}}i}^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde W}}}}_{{\rm{f}}i}}} + }\\ {\sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde W}}_{{\rm{l}}i}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{l}}i}^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde W}}}}_{{\rm{l}}i}}} + \sum\limits_{i = 1}^n {\mathit{\boldsymbol{\tilde W}}_{{\rm{4}}i}^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{{\rm{4}}i}^{ - 1}{{\mathit{\boldsymbol{\dot {\tilde W}}}}_{{\rm{4}}i}}} 。} \end{array} $ | (20) |
根据Ḋ(q)-2C(q,
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}} = - {s^{\rm{T}}}\left( {{\mathit{\boldsymbol{K}}_{\rm{D}}}s + {\mathit{\boldsymbol{E}}_{\rm{l}}} + {\mathit{\boldsymbol{E}}_{\rm{d}}} + {\mathit{\boldsymbol{K}}_{\rm{s}}}{\rm{sat}}\left( s \right)} \right) + }\\ {{s^{\rm{T}}}\left( {{\mathit{\boldsymbol{E}}_{2{\rm{l}}}} + {\mathit{\boldsymbol{E}}_{2{\rm{r}}}}} \right) \le 0。} \end{array} $ | (21) |
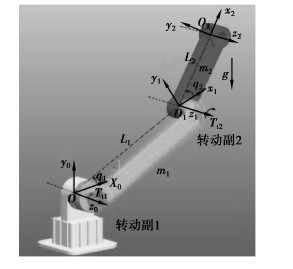
根据二自由度机器人系统的动力学方程(1)式,其中,n=2,机器人各关节低、中、高速的位置指令分别为qd1=0.03 cos t,qd2=0.03 cos t,qd1=-0.3 cos t,qd2=0.3 cos t,qd1=-cos t,qd2=cos t。系统的初始条件,低速为qd(0)=[-0.03 0.03]或者[0 0],中速qd(0)=[-0.030.03],高速qd(0)=[-1 1],z(0)=
| $ \mathit{\boldsymbol{M}}\left( q \right) = \left[ {\begin{array}{*{20}{c}} {\left( {{m_1} + {m_2}} \right)L_1^2 + {m_2}L_2^2 + 2{m_2}{L_1}{L_2}\cos \left( {{q_2}} \right)}&{{m_2}L_2^2 + {m_2}{L_1}{L_2}\cos \left( {{q_2}} \right)}\\ {{m_2}L_2^2 + {m_2}{L_1}{L_2}\cos \left( {{q_2}} \right)}&{{m_2}L_2^2} \end{array}} \right], $ | (22) |
| $ \mathit{\boldsymbol{C}}\left( {q,\dot q} \right) = \left[ {\begin{array}{*{20}{c}} { - {m_2}{L_1}{L_2}\sin \left( {{q_2}} \right){{\dot q}_2}}&{ - {m_2}{L_1}{L_2}\sin \left( {{q_2}} \right)\left( {{{\dot q}_1} + {{\dot q}_2}} \right)}\\ {{m_2}{L_1}{L_2}\sin \left( {{q_2}} \right){{\dot q}_1}}&0 \end{array}} \right], $ | (23) |
| $ \mathit{\boldsymbol{G}}\left( q \right) = \left[ {\begin{array}{*{20}{c}} {\left( {{m_1} + {m_2}} \right)g{L_1}\cos \left( {{q_2}} \right) + {m_2}g{L_2}\cos \left( {{q_1} + {q_2}} \right)}\\ {{m_2}g{L_2}\cos \left( {{q_1} + {q_2}} \right)} \end{array}} \right]。$ | (24) |
| 表 1 机器人参数及其摩擦力参数 |
|
图 4 二关节机器人 |
| 表 2 机器人参数及其摩擦力参数 |
| 表 3 机器人参数及其摩擦力参数 |
图 5~图 14反映了在是否有死区补偿的情况下,二关节机器人的轨迹跟踪、摩擦力矩、控制力矩与时间的关系及摩擦力矩与速度的相图。
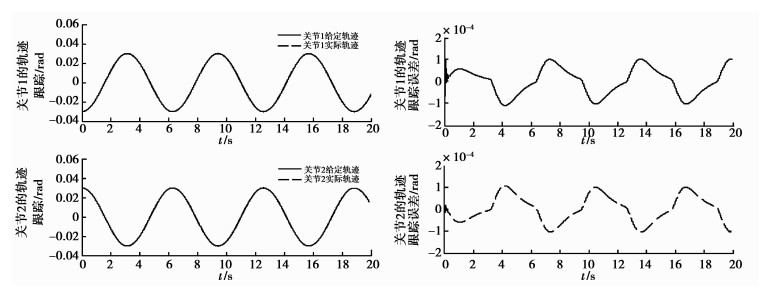
|
图 5 有摩擦和死区补偿时机器人轨迹跟踪及误差 |
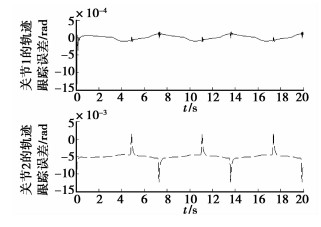
|
图 6 无死区补偿时机器人轨迹跟踪误差 |
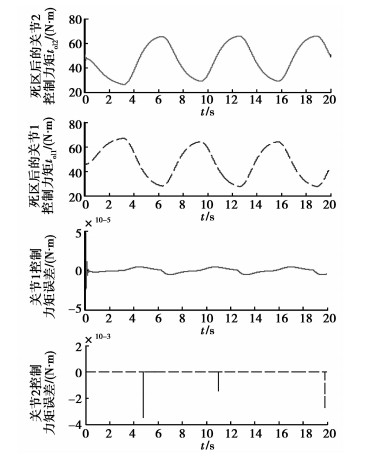
|
图 7 有摩擦和死区补偿时机器人控制力矩及误差 |
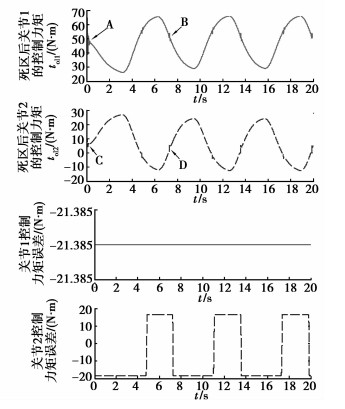
|
图 8 无死区补偿时机器人控制力矩 |
|
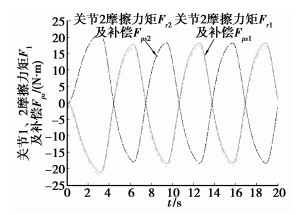
图 9 机器人摩擦及补偿 |
|
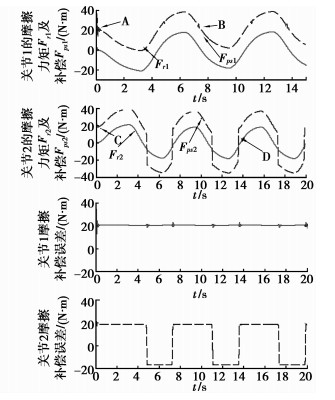
图 10 机器人摩擦力矩(无死区补偿) |
|
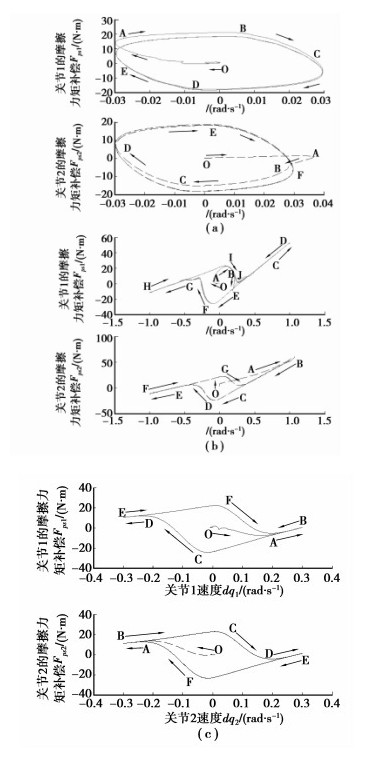
图 11 机器人摩擦模型 (a:dq1=-0.03 cos t,b:dq1=-cos t,c:dq1=-0.3 cos t) |
|
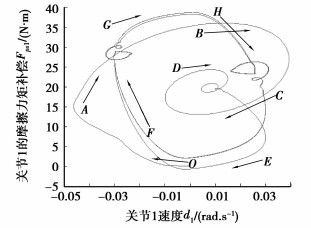
图 12 无死区补偿时第1关节摩擦模型 |
|
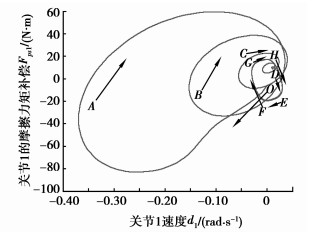
图 13 第1关节摩擦模型(qd1(0)=0) |
|
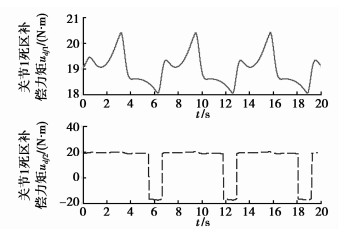
图 14 机器人死区补偿力矩 |
由图 5、图 7、图 9可以看出,在有摩擦和死区补偿时,机器人关节1的轨迹跟踪精度较高,最大位置误差为1.101 6×10-4 rad;死区后的控制力矩τ与死区补偿前的期望控制力矩ud误差小,最大力矩误差为4.726×10-5 N·m,当然,可以通过增大死区自适应律的参数Γli,Γri来提高控制力矩精度,但此时伴随出现的间断脉冲式力矩增大或减小,将对机械臂控制系统的稳定造成不利影响,因此需统一协调控制力矩精度与其稳定性之间的矛盾;动态摩擦力矩的补偿效果也很好,稳定状态最大误差为-1.113 3 N·m。同样地,关节2也将出现类似的规律。
由图 6可以看出,无死区补偿时,关节1的轨迹跟踪精度在启动时和死区附近将降低,最大跟踪误差为-1.333 5×10-3 rad,并将产生不间断脉冲式抖振。
由图 8可以看出,无死区补偿时,关节1的控制力矩将首先在“零”力矩附近(A)及力矩方向发生改变处(B)产生振荡,且关节2的振荡也在一定程度上对关节1的振荡存在着激励的作用,且此时最大力矩误差为21.385 N·m,占总的控制力矩的32.43%。同样地,关节2也存在力矩振荡。
由图 10可以看出,无死区补偿时,关节1的摩擦力矩将主要在由快速增大或减小的过程过渡到向力矩慢速逐渐增大或减小的交点处(A,B)发生振荡,且关节2的振荡也在一定程度上对关节1的振荡存在着激励的作用;且此时的摩擦补偿误差较大,最大为34.358 5 N·m,是稳态时摩擦力矩幅值-21.417 5的1.63倍。与关节1比较,关节2存在类似的规律。
图 11(a)、图 12、图 13是低速运行时,机器人摩擦力矩与速度的相图,达到稳态时类似于菱形。当机器人由启动状态O→平衡状态的运动过程,启动摩擦力矩出现了不同程度的波动,即机器人的初始位置、速度、加速度,对机器人的稳定性影响重大(图 13),特别是在无死区补偿时,其摩擦力矩将出现极限环振荡(图 12)。在初始位置为qd1(0)=0时,机器人的启动力矩震荡幅值较大,为-83.023 6 N·m,是稳态时最大幅值-19.783 6 N·m的4.196 6倍,经过一定时间后,摩擦力矩F与角速度
图 11(b)是高速运行时,机器人摩擦力矩与速度两者的相图,同样出现了Stribeck现象,且当第一关节速度
机器人中速运行时死区补偿力矩udF随时间变化的关系,如图 14所示,其波峰或者波谷的形状与死区的斜率
1) 发现了该2自由度机器人摩擦力矩与速度的规律,即低速时,摩擦以Stribeck效应为主;高速时,以黏性摩擦为主;中速时则兼有两种效应;同时,机器人的启动速度过大将使其启动摩擦力矩出现较大震荡。发现了死区补偿力矩的规律和死区逆模型的估计准确度对机器人精度及控制系统稳定性发挥着至关重要的作用。
2) 缺乏死区模糊补偿,降低了机器人控制精度及品质,引起了控制力矩、摩擦力矩的极限环振荡,影响了系统的稳定性。
| [1] | Kermani M, Wong M, Patel R, et al. Friction compensation in low and high-reversal-velocity manipulators[C]//Proceedings of the 2004 IEEE International Conference on, in Proc. ICRA'04, 2004 IEEE Int. Conf. on Robotics and Automation, April 26-May 1, 2004, New Orleans, LA, USA. Piscataway:IEEE Press, 2004, 5:4320-4325. |
| [2] | 李敏, 王家序, 肖科, 等. 基于模糊RBF神经网络动态摩擦分块补偿的机器人数字鲁棒滑模控制算法[J]. 中国机械工程, 2012, 23(23): 2792–2796. DOI:10.3969/j.issn.1004-132X.2012.23.005 |
| [3] | 李敏. 滤波驱动机构不确定性补偿的机器人鲁棒滑模控制方法研究[D]. 重庆大学博士学位论文, 重庆: 2012. http: //cdmd. cnki. com. cn/Article/CDMD-10611-1013007920. htm |
| [4] | Bona B, Indri M. Friction compensation in robotics:an overview[C]//Proceedings of the 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference, December 12-15, 2005, Seville, Spain. Piscataway:IEEE Press, 2005:4360-4367. |
| [5] |
李妍, 毛志忠, 王琰.
自适应动态径向基函数网络死区补偿控制[J]. 控制理论与应用, 2009, 26(12): 1395–1400.
LI Yan, MAO Zhizhong, WANG Yan. Compensation control for dead-zone by adaptive dynamic radial basis function network[J]. Control Theory & Applications, 2009, 26(12): 1395–1400. (in Chinese) |
| [6] | Lewis F L, Woo K T, Wang L Z, et al. Deadzone compensation in motion control systems using adaptive fuzzy logic control[J]. IEEE Transactions on Control Systems Technology, 1999, 7(6): 731–742. DOI:10.1109/87.799674 |
| [7] | Xu J X, Viswanathan B. Adaptive robust iterative learning control with dead zone scheme[J]. Automatica, 2000, 36(1): 91–99. DOI:10.1016/S0005-1098(99)00100-4 |
| [8] | Hiroaki M, Umeda T, Tanaka Y, et al. LMI-based additive gain for guaranteed cost control of robotic manipulator with deadzone[C]//Proceedings of the 2007 American Control Conference, July 9-13, 2007, New York, NY. Piscataway:IEEE Press, 2007:4077-4082. |
| [9] | 田雨波. 混合神经网络技术[M]. 北京: 科学出版社, 2009. |
| [10] |
谢友柏.
摩擦学系统的系统理论研究和建模[J]. 摩擦学学报, 2010, 30(1): 1–8.
XIE Youbai. On the system theory and modeling of tribo-systems[J]. Tribology, 2010, 30(1): 1–8. (in Chinese) |
| [11] |
刘丽兰, 刘宏昭, 吴子英, 等.
机械系统中摩擦模型的研究进展[J]. 力学进展, 2008, 38(2): 201–213.
LIU Lilan, LIU Hongzhao, WU Ziying, et al. An overview of friction models in mechanical systems[J]. Advances in Mechanics, 2008, 38(2): 201–213. DOI:10.6052/1000-0992-2008-2-J2007-075 (in Chinese) |
| [12] | Canudas D W C, Olsson H, Astrom K J, et al. A new model for control of systems with friction[J]. IEEE Transactions on Automatic Control, 1995, 40(3): 419–425. DOI:10.1109/9.376053 |
| [13] | Armstrong-Hélouvry B, Dupont P, Canudas D W C. A survey of models, analysis tools and compensation methods for the control of machines with friction[J]. Automatica, 1994, 30(7): 1038–1183. |
| [14] | Khayati K, Bigras P. A new model-based dynamic feedback control for systems with friction[C]//Proceedings of the 2007 IEEE International Conference on Systems, Man and Cybernetics, October 7-10, 2007, Montreal, Quebec. Piscataway:IEEE Press, 2007:2710-2715. |
| [15] | Hayward V, Armstrong B, Altpeter F, et al. Discrete-time elasto-plastic friction estimation[J]. IEEE Transactions on Control Systems Technology, 2009, 17(3): 688–696. DOI:10.1109/TCST.2008.2001710 |
| [16] | Kermani M R, Patel R V, Moallem M. Friction identification and compensation in robotic manipulators[J]. IEEE Transactions on Instrumentation and Measurement, 2007, 56(6): 2346–2353. DOI:10.1109/TIM.2007.907957 |
| [17] | Haessig D A, Jr., Fliedland B. On the modeling and simulation of friction[J]. ASME Journal of Dynamic Systems, Measurement, and Control, 1991, 113(3): 354–362. DOI:10.1115/1.2896418 |
| [18] | 刘金琨. 机器人控制系统的设计与MATLAB仿真[M]. 北京: 清华大学出版社, 2008. |
 2013, Vol. 36
2013, Vol. 36

