b. 重庆大学 动力工程学院, 重庆 400044;
c. 重庆大学 城市建设与环境工程学院, 重庆 400044
b. College of Power Engineering, Chongqing University, Chongqing 400044, China;
c. College of Urban Construction and Environmental Engineering, Chongqing University, Chongqing 400044, China
水冷式除渣是大中型煤粉炉常见的一种除渣方式,高温炉渣落入捞渣机冷却水中淬火,冷却后的炉渣通过刮板输送至渣仓,完成除渣过程。炉渣淬火后捞渣机内的冷却水称为含渣水。除渣系统实际运行时,含渣水温度约65 ℃,表面存在较强烈的蒸发。由于蒸发过程伴随着传热及传质,故而含渣水表面蒸发状况对控制捞渣机槽体冷却水温度、确定系统补水量有着重要的影响,因此水冷式除渣系统采用维持水位的方式运行时需要对捞渣机内含渣水的表面蒸发速率进行准确预测,以满足实际运行的需要。
水表面蒸发速率是指单位时间内单位面积上水表面的蒸发量,是衡量水面蒸发快慢的重要参数[1]。迄今有关水面蒸发的研究,大多是在自然环境中对自然水体进行的[2-5],涉及气象、水利等方面。Shammiri和Sartori[6-7]较系统地总结了水面蒸发速率的相关研究成果,并给出水面蒸发速率的部分理论和经验关系式,其中大多基于1802年Dalton提出的计算水面蒸发速率的模型[8]
| $ E=f\left( u \right)\left( {{e}_{\text{s}}}-{{e}_{\text{d}}} \right), $ | (1) |
式中:E为单位时间内的蒸发量;es为蒸发表面温度为Ts时的水汽压力;ed为空气露点温度Td时的水汽压力;f(u)为水平风速u的函数。这些关系式因实验条件和方法的不同而有各自的参数及表达形式[9-10]。
此外,Vinnichenko Nikolay等[11]用数值方法研究了水面蒸发的影响因素,并与现有经验公式对比,认为瑞利数与水表面蒸发有很大的相关性;Assouline和Narkis[12]从抑制水面蒸发的角度研究了表面覆盖分数对蒸发效率的影响,发现蒸发效率与覆盖分数的平方根成正比;Drisdell Walter、Saykally Richard[13]研究了表面活性剂离子对蒸发速率的影响,实验发现高氯酸钠溶液的蒸发速率较纯净水低25%,Cohen Ronald等[13-14]从分子动力学角度对此结果进行了分析。
目前的研究已可以实现对自然水体蒸发速率的定量计算,在现代工业中经常需要对类似上述含渣水等非自然水体的表面蒸发速率进行预测。笔者对水冷式除渣系统的含渣水表面蒸发速率进行了实验,得到了1个大气压下风速为0.5 m/s时含渣水表面蒸发速率与各影响因素之间的实验关联式;通过改变含渣水浓度进行表面蒸发速率测量实验,并与同实验条件下纯水表面蒸发速率情况作对比,从热力学角度分析了表面水温、水体组分含量等对表面蒸发速率影响的内在原因。
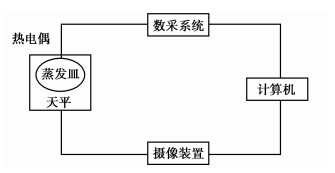
1 实验方法水的蒸发过程是液面相变向环境传质的过程,因此实验采用直接计量蒸发器皿中水的质量变化的方法测定蒸发速率。采用热电偶测量、数采系统监测和采集蒸发水面的温度,摄像头记录天平的读数变化,然后逐帧分析实验读数视频,采集蒸发过程水体质量变化的数据。实验装置如图 1所示。
|
图 1 实验装置示意图 |
实验所用到的器材及参数如表 1所示。
| 表 1 实验器材 |
实验采用的高精度数字式天平量程较小,为保证测量,不便在蒸发皿上架设恒温装置,一次实验过程为水体的自然冷却过程,实验步骤如下:
1) 蒸发皿中盛约80 ℃的待测液置于天平上,热电偶探头安装在液面下5 mm处,温湿度计放置在蒸发皿附近,外置摄像头对准分析天平的显示屏。
2) 记录蒸发液的初始温度和蒸发环境的温度、相对湿度。
3) 数采装置和摄像头连续记录蒸发液的温度及质量的变化,直至蒸发液冷却至室温。
4) 重复以上步骤若干次,得到足够的实验数据。数据处理时,忽略短时间内水温的变化,认为2 s内水面在恒定的水温下蒸发,记录这段时间的蒸发量,就可计算得到对应水温下的蒸发速率。大量重复实验,得到对应水温下的多组蒸发数据,据此探寻蒸发规律。
煤粉燃烧后灰渣成分复杂,主要含有SiO2、Al2O3、CaO、Fe2O3和MgO等物质。笔者采用陕西国华锦界电厂600 MW机组除渣系统的含渣水进行实验,经检测,含渣水溶液PH值约为9,呈碱性,其主要成分含量见下表。
| 表 2 含渣水主要成分及含量 |
实验时含渣水温度变化范围30~75 ℃,其他影响因素的控制情况分别为相对湿度RH=40%~90%,风速稳定在0.5 m/s,环境压力为1个大气压。
2 实验结果及分析 2.1 实验结果影响水面蒸发速率的因素较多,图 2、图 3分别给出了控制变量条件下单因子变量与蒸发速率的关系,直观地描述各影响因素对含渣水表面蒸发速率的作用。
|
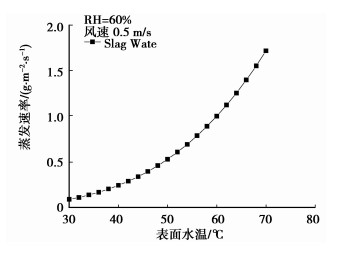
图 2 表面水温与蒸发速率的关系 |
|
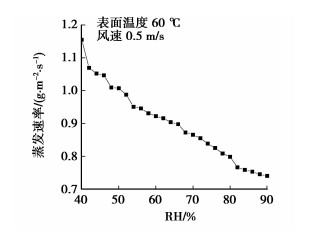
图 3 相对湿度与蒸发速率的关系 |
由图 2可知风速0.5 m/s,相对湿度60%时,表面温度越高,水面蒸发速率越快;图 3给出的是风速0.5 m/s,表面水温60 ℃时,相对湿度越大,水面蒸发速率越慢。
用Levenberg-marquardt法和通用全局优化法[15]对所有的实验数据进行多元非线性回归处理,得到了以表面水温和相对湿度为自变量,水面蒸发速率为因变量的函数表达式
| $ \begin{align} &E=(0.001{{T}^{2}}-0.0552T+ \\ &\ \ \ 0.9121){{(1-{{r}^{2}})}^{0.0456}}, \\ \end{align} $ | (1) |
式中:E表示水面蒸发速率,g/(m2·s);T表示水表面温度,℃;r表示蒸发环境的相对湿度,计算时用小数表示。关联式的相关系数为0.96,适用于1个大气压,风速0.5 m/s,表面水温30~75 ℃,相对湿度40%~90%的场所。
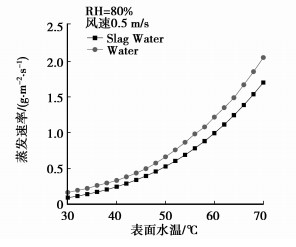
作为对比,笔者采用同样的实验方法对纯水进行了实验。图 4、图 5给出的是相同实验条件下2种水质水面蒸发速率随水面温度变化的比较,图 4的实验条件为RH=50%,图 5的实验条件为RH=80%。

|
图 4 RH=50%时蒸发速率对比 |
|
图 5 RH=80%时蒸发速率对比 |
两图的比较结果均表明相同温度下纯水表面蒸发速率较含渣水水面蒸发速率快。在实验范围内,温度大于50 ℃时,纯水蒸发速率约为含渣水蒸发速率的1.1~1.2倍,30~50 ℃时,这个倍数略大一些,且这一现象不受相对湿度变化的影响,是水质的不同导致了2种水面蒸发速率产生了差异。
为了进一步探究产生这种差异的原因,笔者又做了另外1组实验。将含渣水溶液按1:1和1:2的比例用水稀释,分别测量稀释后的溶液表面蒸发速率。实验结果见图 6。

|
图 6 溶质浓度对水面蒸发速率的影响 |
图 6描述的是RH=50%时,1:1和1:2稀释含渣水表面蒸发速率与纯水和原含渣水表面蒸发速率的对比,显然相同温度下稀释后的溶液表面蒸发速率介于纯水和原含渣水表面蒸发速率之间,表明含渣水溶液的浓度对表面蒸发速率产生了影响。比较图中相同温度下不同浓度的溶液表面蒸发速率,可以看出溶液的浓度越小,表面蒸发速率越快。图 6中稀释后的含渣水表面蒸发速率更靠近原含渣水的表面蒸发速率,而不同比例的含渣水蒸发速率曲线靠得很近,计算发现相同温度下不同3种浓度的含渣水表面蒸发速率的改变在10%以内,说明一定范围内浓度的改变对含渣水的表面蒸发速率影响不大。
2.2 结果分析蒸发现象的基本原理是液体内分子不规则的运动,动能较大的分子突破液面表面自由能逸出,宏观上由液相变为气相。表面自由能定义为[16]
| $ \gamma =\left( \frac{\text{d}G}{\text{d}T} \right)T, p, $ | (2) |
从热力学角度看,其物理意义为增加单位表面积时Gibbs自由能的增量,又称表面Gibbs自由能。Gibbs自由能不仅取决于温度和压力,还取决于体系的各组分的量n1,n2…,即dG=f(T,p,n1,n2,…)。此时G的全微分为[17-19]
| $ \begin{align} &\left( \frac{\text{d}G}{\text{d}T} \right){{n}_{1}}, {{n}_{2}}, p\text{d}T+ \\ &\left. \left( \frac{\text{d}G}{\text{d}T} \right){{n}_{1}}, {{n}_{2}}, T\text{d}p+\frac{\text{d}G}{\text{d}{{n}_{1}}} \right)T, p, {{n}_{2}}\text{d}{{n}_{1}}+\cdots。\\ \end{align} $ | (3) |
上式表明表面自由能会因温度改变dT,压力改变dp以及组分量改变dn1,dn2而发生变化。
根据热力学的基本公式,对σ表面,有
| $ \text{d}{{G}^{\sigma }}=-{{S}^{\sigma }}\text{d} T+\gamma\text{d}A+\sum{\mu i\text{d}{{n}^{\sigma }}}, $ | (4) |
定温时,
| $ \text{d}{{G}^{\sigma }}=\gamma \text{d}A+\sum{\mu i\text{d}{{n}^{\sigma }}}, $ | (5) |
式中,μi为组分的化学势。
又据热力学偏摩尔量公式,σ面的Gibbs函数为
| $ {{G}^{\sigma }}=\sum{n_{^{i}}^{\sigma }{{\mu }_{i}}}+\gamma A, $ | (6) |
该式的全微分式为
| $ \text{d}{{G}^{\sigma }}=\sum{{{\mu }_{i}}\text{d}{{n}^{\sigma }}}\text{+}\sum{n_{^{i}}^{\sigma }\text{d}{{\mu }_{i}}}\text{+}\gamma \text{d}A\text{+}A\text{d}\gamma 。$ | (7) |
比较式(5)与式(7)得
| $ \text{d}\gamma \text{= }-\sum{\frac{n_{^{i}}^{\sigma }}{A}}\text{d}{{\mu }_{i}}=-\sum{{{\mathit{\Gamma }}_{\mathit{i}}}\text{d}{{\mu }_{i}}}。$ | (8) |
式中:Γi为单位面积上组分i的过剩量,也称组分i的过剩浓度或表面吸附量。
对于2组分体系,上式变为
| $ \text{d}\gamma \text{=}-{{\mathit{\Gamma }}_{1}}\text{d}{{\mu }_{1}}-{{\mathit{\Gamma }}_{2}}\text{d}{{\mu }_{2}}。$ | (9) |
式中:1代表溶剂,2代表溶质。
根据吉布斯相界面理论,认为溶剂的表面过剩量等于零Γ1(1)=0,以此来规定溶质的量,于是有
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2^{(1)} = - {\left( {\frac{{\partial \gamma }}{{\partial {\mu _2}}}} \right)^{\rm{T}}} $ | (10) |
对理想稀溶液,溶液中溶质的化学式为
| $ {{\mu }_{2}}=\mu _{2}^{\Theta }\left( T \right)+RT\ln \frac{{{c}_{2}}}{{{c}^{\Theta }}}, $ | (11) |
| $ \text{d}{{\mu }_{2}}=RT\text{d}\ln \frac{{{c}_{2}}}{{{c}^{\Theta }}}, $ | (12) |
式中,c表示溶液浓度。则有
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_2^{(1)} = - \frac{1}{{RT}}{\left( {\frac{{\partial \gamma }}{{\partial \ln \frac{{{c_2}}}{{{c^\Theta }}}}}} \right)^{\rm{T}}}。$ | (13) |
式(13)描述了表面自由能与温度、溶质浓度和表面过剩量之间的关系。若
气液界面上持续进行着分子的迁移交换,由液相到气相的迁移速率大于由气相到液相的迁移速率时,就会出现蒸发现象。研究发现界面单个分子的迁移速率为[15]
| $ \beta =\alpha {{\left( 2\pi mkT \right)}^{0.5}}{{p}_{0}}, $ | (13) |
式中:α为黏性系数;p0是液体的平衡气压;m表示分子量;k指Boltzmann常数。
显然温度越高,界面分子的迁移速率越大,这会增大表面的总熵,因而减少其自由能,表面自由能减小,表面对分子的束缚能力降低,蒸发速率增大,如图 2所示。
3 结论对1个大气压下,风速为0.5 m/s时非自然水体含渣水表面蒸发速率进行了实验,得到了适用于水温30~75 ℃,相对湿度在40%~90%范围内的含渣水表面蒸发速率实验关联式,其相关系数为0.96。实验测量了不同浓度的含渣水水面蒸发速率,并与纯水表面蒸发速率的实验结果对比,计算发现实验范围内,相同条件下水温高于50 ℃时纯水表面蒸发速率约为含渣水表面蒸发速率的1.1~1.2倍,水温低于50 ℃时倍数略高;而一定范围内含渣水浓度的改变对表面蒸发速率的影响较小,实验范围内浓度的改变对蒸发速率的影响在10%以内。此外,文中从热力学角度分析讨论了影响含渣水气液界面上的蒸发速率的内在原因,即水面的温度和组分含量改变了水面的表面自由能,从而影响了水面的蒸发速率,呈碱性的无机盐组分增大了表面自由能,抑制了水面蒸发速率,无机盐浓度越高,抑制作用越明显;水温的升高降低了表面自由能,使水面蒸发速率增加。
| [1] |
耿江涛, 李相一, 邢广磊, 等.
水表面蒸发速率的实验研究[J]. 电源技术, 2010(5): 470–472.
GENG Jiangtao, LI Xiangyi, XING Guanglei, et al. An experimental study on water surface evaporation rate[J]. Chinese Journal of Power Sources, 2010(5): 470–472. (in Chinese) |
| [2] | Inoueh I. Water evaporation amount in surface[J]. The Air Conditioning Sanitary Engineering, 1962, 36(1): 144–145. |
| [3] | Ueda M B. Rate of evaporation of water by turn disk[J]. Application Physics, 1962, 31(6): 492–493. |
| [4] | Ueda M B. Rate of evaporation of water by forced convection[J]. Application Physics, 1960, 29(1): 443–451. |
| [5] | Ueda M B. Humidity and evaporation[M]. Corona: Corona Publishing Co. LCD, 2000. |
| [6] | Shammiri-Al M. Evaporation rate as a function of water salinity[J]. Desalination, 2002, 150(2): 189–203. DOI:10.1016/S0011-9164(02)00943-8 |
| [7] | Sartori E. A critical review on equations employed for the calculation of the evaporation rate from free water surface[J]. Solar Energy, 2000, 68(1): 77–89. DOI:10.1016/S0038-092X(99)00054-7 |
| [8] | 朱岗崑. 自然蒸发的理论及应用[M]. 北京: 气象出版社, 2000. |
| [9] | Tang R S, Etzion Y. Molecular dynamics simulation of a thin water layer evaporation and evaporation coefficient[J]. Building and Environment, 2004, 39: 77–86. DOI:10.1016/j.buildenv.2003.07.007 |
| [10] | Sakuma T O. Study of heat collection and extraction method in solar pond[J]. The Reports of Central Research Institute of Electric Power Industry, 1986, 28081: 11–13. |
| [11] | Vinnichenko N A, Uvarov A V, Vetukov D A, et al. Direct computation of evaporation rate at the surface of swimming pool[J]. Recent Researches in Mechanics, 2011: 120–124. |
| [12] | Assouline S, Narkis K. Evaporation suppression from water reservoirs:efficiency considerations of partial covers[J]. Water Resources Research, 2009, 47(7). |
| [13] | Drisdell W S, Saykally R J, Cohen R C. Effect of surface active ions on the rate of water evaporation[J]. Journal of Physical Chemistry, 2010, 114(27): 11880–11885. |
| [14] | Škvarla J, Nagy M. Do partially wettable surfaces influence the drying kinetics of microliter water drops beyond the evaporation models[J]. Journal of Physical Chemistry, 2011, 115(38): 18670–18682. |
| [15] | 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997. |
| [16] | 林宪杰, 许和允, 殷保华, 等. 物理化学[M]. 北京: 科学出版社, 2010. |
| [17] | 颜肖慈, 罗明道. 界面化学[M]. 北京: 化学工业出版社, 2005. |
| [18] | 范康年. 物理化学[M]. 2版. 北京: 高等教育出版社, 2005. |
| [19] | Myers D. 表面界面和胶体: 原理及应用[M]. 吴大诚, 朱谱新, 王罗新, 等译. 北京: 化学工业出版社, 2005. |
 2013, Vol. 36
2013, Vol. 36

