太阳能热发电技术是太阳能研究领域的前沿课题,吸热器作为碟式太阳能热发电过程中的能量转换装置在整个发电系统中起到了重要的作用,其性能的改善对提高整个发电系统的热电转换效率具有重要意义。虽然吸热器的结构形式在国内外的研究中呈现多元化的态势,但腔式吸热器因其较高的热传递效率仍获得了较多的关注。目前广泛研究和实际应用的腔式吸热器形状主要有方形、圆柱形、半球形、平顶锥形等。其中对方形腔式吸热器的研究最多也最广,而对于圆柱形腔式吸热器的研究相对较少。
Koenig和Marvin[1]提出了考虑圆柱形腔式吸热器倾角和采光口大小对自然对流热损失影响的传热关系式。Siebers和Kraabel[2]在对圆柱形腔式吸热器开展实验研究的基础上,提出了一个结构简单,使用方便,但是计算精度有限的努塞尔特数与格拉晓夫数和吸热器壁温之间的关系式。Stine和Mcdonald[3]在上述模型的基础上,对一个圆柱平截头体复合结构的太阳能腔式吸热器进行了实验,提出了考虑工作壁温、倾角、采光口大小对吸热器对流热损失影响的传热模型,提出了计算精度较高,结构简单、被广为采用的实验关联式。Taumoefolau和Paitoonsurikam等[4-6]也在定壁温的工况下对圆柱形腔式吸热器的对流换热特性进行了实验研究,获得了多个关于计算圆柱形腔式吸热器自然对流热损失的努塞尔特数传热关系式。
值得指出的是,以上研究都是在定壁温的热边界条件下进行的,而根据太阳能辐射热流的特性,腔式吸热器的热边界条件近似为定热流更符合实际情况[7-9],同时与定壁温的热边界条件不同,定热流时的热辐射对腔体内的自然对流有着重要的影响,因此定热流时的腔式吸热器热损失特性要比定壁温时复杂。Chakroun[10]对1个只有一侧全开的方形腔体在某一个或某几个壁面处于定热流边界条件下的传热特性进行了实验研究。而目前对圆柱形腔式吸热器在定热流条件下热损失特性的实验研究还开展得较少。通过建立腔式吸热器热损失性能测试实验台,采用电加热的方法,分别在所有壁面加热和只有底面(开口对面)加热2种情况下,探讨腔式吸热器的倾角和热流密度等参数对热损失的影响,从而为圆柱形腔式吸热器的设计提供理论参考。
1 实验装置实验装置如图 1所示。其中吸热器壁面材料为304不锈钢(06Cr19Ni10),其耐腐性和成型性都很好,且能耐1 000 ℃的高温,满足实验要求。

|
图 1 实验装置图 |
腔体的保温材料选用单层厚度为5 mm的陶瓷纤维纸,其导热系数与温度的关系拟合为λ=-0.070 5+4×10-4T-2×10-7T2(其中T为吸热器达到稳态后腔体壁面和保温层外表面温度的平均值,K);陶瓷纤维纸比保温棉、针刺毯等普通保温材料的导热系数更低,且连续使用温度可达800 ℃,优于传统的保温材料。
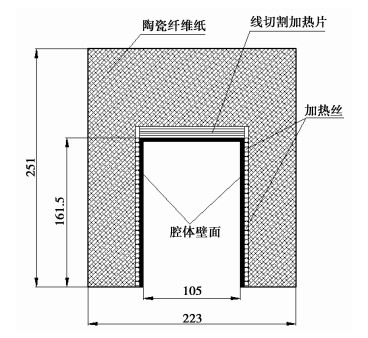
腔体结构如图 2所示,其中腔体一侧全开,即开口率为1。实验过程采用电加热方式来实现对圆柱形腔体外壁面的加热,其中,对腔体的侧面和底面分别通过2个独立的回路进行加热,即侧面加热通过在侧面均匀缠绕直径为2mm,材料为OCr25Al5的加热丝来实现;而底面加热则采用线切割技术加工的不锈钢片。用2个调压器分别控制每个回路的输入功率,既可以实现腔体侧面和底面的输入热流密度相等,又可以方便实现不同的加热情况。
|
图 2 腔体结构示意图(单位:mm) |
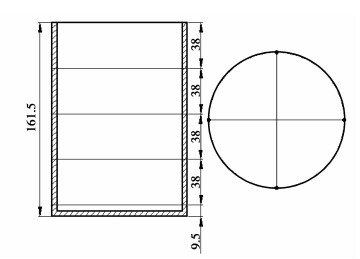
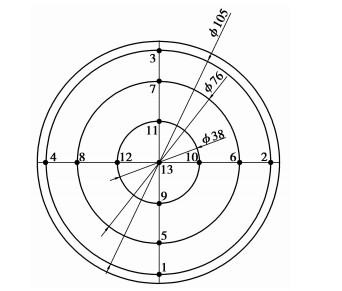
腔体的侧面和底面分别铆接16只和13只K型热电偶测温,其中,侧面取与底面平行的4个圆周,每个圆周对称铆接4支热电偶,如图 3所示;底面取以腔体底面圆心为圆心,直径为38、76、105 mm的3个同心圆,每个圆周上对称铆接4支热电偶,圆心处也铆接1支热电偶,如图 4所示。通过XMTA-JK408型温控仪来显示和记录系统达到稳态后腔体各测点的温度。包裹好保温材料的吸热器通过钢支架固定到实验台上,吸热器的倾角通过数字角度尺实现精确调节。腔体的倾角定义如下:如果腔体开口方向水平朝右,则其倾角φ为0°;顺时针方向旋转,如果腔体开口方向垂直向下,则其倾角φ为90°。
|
图 3 侧面热电偶布置示意图(单位:mm) |
|
图 4 底面热电偶布置示意图(单位:mm) |
由于腔式吸热器与环境相比无穷小,因此计算辐射热损失的公式可近似为[11]
| $ {P_r} = {\varepsilon _{\rm{a}}}\sigma \left( {T_{\rm{w}}^4 - T_{\rm{s}}^4} \right){A_2}, $ | (1) |
式中:σ为斯忒藩波尔兹曼常量,W/(m2·K4);Tw为腔体内壁平均温度,K;Ts为环境温度,K;A2为采光口面积,m2;εa为腔体内壁面的有效发射率,可以采用Umarov等[12]提出的方法进行计算
| $ {\varepsilon _{\rm{a}}} = \frac{{{\varepsilon _{\rm{w}}}}}{{1 - \left( {1 - {\varepsilon _{\rm{w}}}} \right)\left( {1 - {A_2}/{A_1}} \right)}}, $ | (2) |
式中:εw为腔体壁面材料的热发射率;A1为腔式吸热器的内腔壁表面积,m2。
2.2 导热损失的计算腔体的导热损失为腔体侧面导热损失和底面导热损失之和,即
| $ {P_{{\rm{cond}}}}{\rm{ = }}\frac{{2\pi H\lambda \left( {{t_1} - {t_2}} \right)}}{{\ln \left[{\left( {r + {\delta _1}} \right)/r} \right]}} + \frac{{{A_3}\lambda \left( {{t_3} - {t_4}} \right)}}{{{\delta _2}}}, $ | (3) |
式中:H为吸热器内腔高度,m;r为吸热器外半径,m;δ1为吸热器侧面保温材料厚度,m;δ2为吸热器底面保温材料厚度,m;T1为吸热器侧面的平均壁温,℃;T2为保温层外侧面的平均温度,℃;T3为吸热器底面的平均壁温,℃;T4为保温层底面的平均温度,℃;A3为吸热器底面面积,m2;λ为保温材料的导热系数,W/(m·K)。
2.3 自然对流热损失的计算当系统达到稳态后,输入系统的功率通过3种方式损失掉,即腔体内壁与环境之间的辐射换热损失Pr,腔体通过保温材料的导热损失Pcond以及腔体内壁与空气的自然对流热损失Pc,由能量平衡可知
| $ {P_{\rm{c}}}{\rm{ = }}P - {P_r} - {P_{{\rm{cond}}}} $ | (4) |
因此,正确计算腔体的辐射热损失和导热损失是计算自然对流热损失和实验数据处理的关键。
2.4 自然对流热损失Nuc与辐射热损失Nur的计算为反映自然对流热损失的大小,引入自然对流热损失努塞尔特数Nuc为
| $ N{u_{\rm{c}}}{\rm{ = }}\frac{{{q_{\rm{c}}}d}}{{\left( {{T_{\rm{w}}} - {T_{\rm{s}}}} \right){\lambda _1}}}{\rm{ = }}\frac{{{p_{\rm{c}}}d}}{{\left( {{T_{\rm{w}}} - {T_{\rm{s}}}} \right){A_1}{\lambda _1}}}, $ | (5) |
式中:d为吸热器的采光口直径,m;λ1为环境温度Ts下的空气导热系数,W/(m·K);qc为自然对流热损失的热流密度,W/m2。
同样,为反映辐射热损失的特性,定义辐射热损失的努塞尔特数Nur为
| $ N{u_{\rm{r}}}{\rm{ = }}\frac{{{q_{\rm{r}}}d}}{{\left( {{T_{\rm{w}}} - {T_{\rm{s}}}} \right){\lambda _1}}}{\rm{ = }}\frac{{{p_{\rm{r}}}d}}{{\left( {{T_{\rm{w}}} - {T_{\rm{s}}}} \right){A_1}{\lambda _1}}}, $ | (6) |
式中,qr为辐射热损失的热流密度,W/m2。
3 实验结果及分析在系统达到稳态后,记录吸热器壁面(包括侧面和底面)所布热电偶的温度、保温材料外部表面温度以及环境温度。改变腔式吸热器的倾角φ和电源的输入功率,测得不同工况下的热损失数据。通过计算分别求得辐射热损失Pr,导热损失Pcond,自然对流热损失Pc,自然对流热流密度qc,努塞尔特数Nuc,格拉晓夫数Grc以及辐射热损失热流密度qr,努塞尔特数Nur和格拉晓夫数Grr。
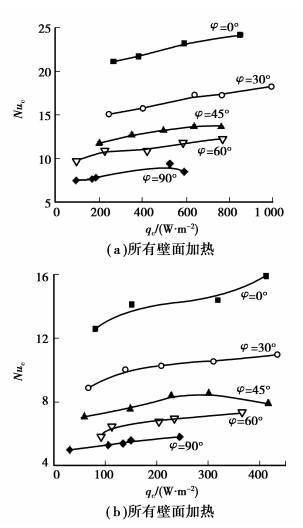
图 5给出了2种加热情况下腔式吸热器在不同的倾角φ下自然对流热损失的努塞尔特数Nuc随自然对流热流密度qc的变化规律。从图中可以看出,当倾角φ一定时,吸热器自然对流热损失的Nuc随着自然对流热流密度qc的增大而增大,但增大趋势较缓慢,这可能是由于在倾角φ一定时,qc的增大也会导致壁温Tw升高,但壁温Tw的升高幅度小于qc的增大幅度;当自然对流热损失qc一定时,自然对流热损失的Nuc数随倾角的增大而减小,这是由于当qc一定时,随着倾角φ的增大,自然对流强度变弱,腔体壁温Tw升高的缘故。另外,通过比较图 5(a)和(b)可看出,尽管2种加热情况下的Nuc随自然对流热流密度qc的变化规律类似,但在相同的条件下,只有底面加热时的Nuc要小于所有壁面加热时的Nuc,即2种情况下的自然对流热损失性能存在差异,这是由于在只有底面加热时,受热空气位于腔体内的上部区域,即滞止区内,不易形成自然对流;而在所有壁面加热时,由于腔体侧面也被加热,存在受热空气向上流动形成自然对流的可能。
|
图 5 不同倾角φ下Nuc与qc的关系曲线 |
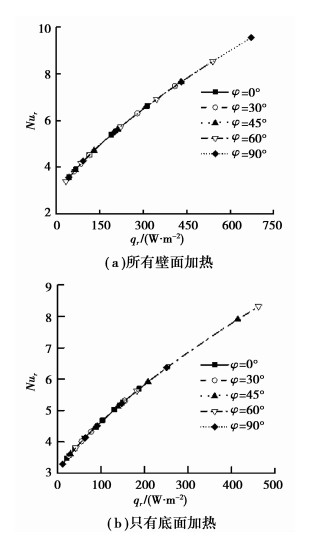
图 6给出了2种加热情况下吸热器在不同倾角φ下辐射热损失的Nur数随辐射热损失热流密度qr的变化规律。从图中可看出,当倾角φ一定时,2种加热情况下吸热器辐射热损失的Nur都随热流密度qr的增大而显著增大,这与自然对流热损失的Nuc随着自然对流热流密度qc的增大而略微增大不同;不同倾角φ下的辐射热损失的Nur数随辐射热损失的热流密度qr的变化曲线基本重合,这说明,当辐射热损失热流密度qr一定时,倾角对辐射热损失的努塞尔特数Nur影响很小,这可能是由于在不同的倾角φ下,只要辐射热损失的热流密度qr保持不变,腔体壁面的平均温度也会近似保持不变的缘故。这一结果与文献[13-14]在吸热器腔体处于定壁温工况下得到的结论类似,即倾角对辐射热损失几乎没有影响。但是仍有差别:定热流工况下倾角对辐射热损失的影响比定壁温工况略大。另外,通过比较图 6(a)和(b)可以看出,当辐射热损失的热流密度和倾角相同时,所有壁面加热时的Nur和单独底面加热时的Nur偏差很小,这跟图 5所反映的自然对流热损失的Nuc在2种情况下的规律不同,这也说明加热位置对辐射热损失性能的影响要比对自然对流热损失的影响小。
|
图 6 不同倾角φ下Nur与qr的关系曲线 |
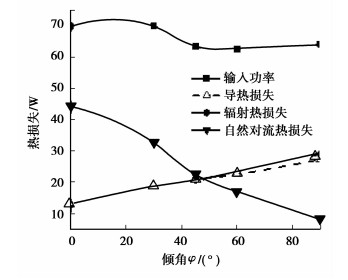
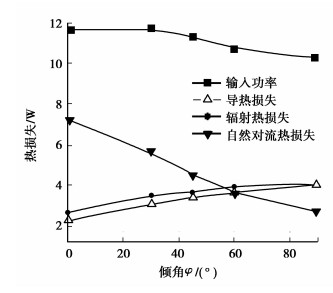
图 7为所有壁面加热且输入功率为66 W左右时,腔体的辐射热损失、导热损失和自然对流热损失随倾角φ的变化关系曲线。图中输入功率曲线出现波动的原因是由于在输入电压一定时,腔体倾角的变化会导致系统达到稳态后腔体的平均壁温略有变化,因此腔体侧面的加热丝和底面的加热片的电阻也随之变化,从而使得稳态后系统的输入功率也有所变化。如当吸热器的倾角为30°时,稳态后测得输入功率为70.20 W,与初始输入功率66 W最大偏差仅为6.36%,因此可以近似看作定热流工况。图 8为只有底面加热且输入功率为11 W左右时,腔体的辐射热损失、导热损失和自然对流热损失随倾角φ的变化关系曲线。当吸热器的倾角为30°时,稳态后测得输入功率为11.77 W,与初始输入功率11 W偏差为6.97%;而当倾角为90°时,与初始输入功率的偏差为6.72%,与图 7相比偏差稍大,这是由于与图 7的所有壁面加热情况相比,只有底面加热时的系统电阻要小得多,从而使得壁温的变化所引起的加热片电阻变化在加热片总电阻中所占的比例增大,导致在稳态下测得的输入功率与初始输入功率的偏差增大。不过在工程允许偏差范围之内,仍然可以近似看作定热流工况。2种加热情况下的自然对流热损失都是随倾角φ的增大而减小,而导热热损失和辐射热损失则随倾角φ的增大而增大,但增大的幅度相对较小,说明自然对流热损失相对于辐射热损失和导热损失受角度的变化影响较大;并且2种情况下的导热损失都小于辐射热损失。但对所有壁面加热情况,在倾角较小时,导热热损失和辐射热损失相差不大;对只有底面加热情况,在倾角较大时,两者差异减小。
|
图 7 所有壁面加热且输入功率为66 W左右时不同热损失随倾角φ的变化曲线 |
|
图 8 只有底面加热且输入功率为11 W左右时不同热损失随倾角φ的变化曲线 |
为获得2种情况下自然对流热损失的Nuc和辐射热损失的Nur随倾角φ,自然对流热流密度qc和辐射热损失热流密度qr的实验关联式,借助文献[13]在辐射热损失的Nur中耦合格拉晓夫数的方法,同时定义定热流边界条件下的自然对流热损失的格拉晓夫数Grc和辐射热损失的格拉晓夫数Grr为
| $ G{r_{\rm{c}}}{\rm{ = }}\frac{{g{\alpha _{\rm{V}}}{q_{\rm{c}}}{d^4}}}{{{\lambda _1}{v^2}}}, G{r_{\rm{r}}}{\rm{ = }}\frac{{g{\alpha _{\rm{V}}}{q_{\rm{r}}}{d^4}}}{{{\lambda _1}{v^2}}}, $ | (7) |
式中:g为重力加速度,m/s2;αV为空气体胀系数,K-1;ν为空气的运动粘度,m2/s;定性温度取环境温度Ts。
通过实验数据拟合,整理出的实验关联式如下所有壁面加热时:
| $ N{u_{\rm{c}}}{\rm{ = 0}}{\rm{.06252}}Gr_{_{\rm{c}}}^{0.25}{\left( {1{\rm{ + }}\cos \varphi } \right)^{1.19286}}{\left( {\frac{{{q_{\rm{c}}}}}{{\sigma T_{\rm{s}}^4}}} \right)^{ - 0.10663}}, $ | (8) |
| $ N{u_{\rm{r}}}{\rm{ = 0}}{\rm{.06140}}Gr_{\rm{r}}^{0.25}{\left( {1{\rm{ + }}\cos \varphi } \right)^{ - 0.05317}}{\left( {\frac{{{q_{\rm{r}}}}}{{\sigma T_{\rm{s}}^4}}} \right)^{0.09534}}。$ | (9) |
只有底面加热时:
| $ N{u_{\rm{c}}}{\rm{ = 0}}{\rm{.04429}}Gr_{_{\rm{c}}}^{0.25}{\left( {1{\rm{ + }}\cos \varphi } \right)^{1.11272}}{\left( {\frac{{{q_{\rm{c}}}}}{{\sigma T_{\rm{s}}^4}}} \right)^{ - 0.13912}}, $ | (10) |
| $ N{u_{\rm{r}}}{\rm{ = 0}}{\rm{.05769}}Gr_{\rm{r}}^{0.25}{\left( {1{\rm{ + }}\cos \varphi } \right)^{ - 0.03564}}{\left( {\frac{{{q_{\rm{r}}}}}{{\sigma T_{\rm{s}}^4}}} \right)^{0.00823}}。$ | (11) |
所有壁面加热时,采用实验关联式(8)计算所得的努塞尔特数Nuc,cor与通过实验数据计算所得的努塞尔特数Nuc,exp的对比发现,40%的Nuc,cor与Nuc,exp的偏差在±10%内,而92%的Nuc,cor与Nuc,exp的偏差在±20%内。同样,通过式(9)计算所得的努塞尔特数Nur,cor与通过实验数据计算所得的努塞尔特数Nur,exp比较发现,100%的Nur,cor与Nur,exp的偏差在±10%内。只有底面加热时,采用实验关联式(10)计算所得的努塞尔特数Nuc,cor与通过实验数据计算所得的努塞尔特数Nuc,exp的对比发现,32%的Nuc,cor与Nuc,exp的偏差在±10%内,而80%的Nuc,cor与Nuc,exp的偏差在±20%内。同样,通过实验关联式(11)计算所得的努塞尔特数Nur,cor与通过实验数据计算所得的努塞尔特数Nur,exp比较发现,88%的Nur,cor与Nur,exp的偏差在±10%内。
4 结语通过建立腔式吸热器热损失性能测试实验台,在定热流工况下,分整体加热和只有底面加热2种情况对一侧全开式圆柱形腔式吸热器的热损失特性进行了实验研究,得到了可用于工程设计的实验关联式。结果表明,1)在相同的倾角φ下,自然对流热损失的Nuc数和辐射热损失的Nur数都随对应的热流密度的增大而增大,但增幅不同;2)吸热器的自然对流热损失qc一定时,自然对流的Nuc数随倾角φ的增大而减小;而辐射热损失qr一定时,倾角φ对辐射换热的Nur数影响很小;3)输入功率一定时,吸热器的自然对流热损失随倾角φ的增大而减小,导热损失和辐射损失随倾角φ的增大而增大,但增幅不大;4)2种加热情况下的热损失性能存在一定的差异,加热位置对辐射热损失性能的影响要比对自然对流热损失的影响小。
| [1] | Koenig A A, Marvin M. Convection heat loss sensitivity in open cavity solar receivers[R]. USA:Department of Energy, 1981. |
| [2] | Siebers D L, Kraabel J S. Estimating convective energy losses from solar central receivers[R]. United States:Sandia National Labs, 1984. |
| [3] | Stine W B, McDonald C G. Cavity receiver convective heat loss[C]//Proceedings of the International Solar Energy Society (ISES)Solar World Conference, September 4-8, 1989, Kobe, Japan.[S.l.]:[S.n.], 1989. |
| [4] | Taumoefolau T, Lovegrove K. An experimental study of natural convection heat loss from a solar concentrator cavity receiver at varying orientation[C/OL]//Proceedings of the 40th Annual Conference of the Australian and New Zealand Solar Energy Society, November 25-December 2, 2002, Newcastle, Australia.[2011-10-22]. http://solar-thermal.anu.edu.au/files/2010/02/Newcastle02Tui.pdf . |
| [5] | Taumoefolau T, Paitoonsurikarn S, Hughes G, et al. Experimental investigation of natural convection heat loss from a model solar concentrator cavity receiver[J]. Journal of Solar Energy Engineering, 2004, 126(2): 801–807. DOI:10.1115/1.1687403 |
| [6] | Paitoonsurikarn S, Lovegrove K. A new correlation for predicting the free convection loss from solar dish concentrating receivers[C]. Proceedings of the 44th Conference of the Australia and New Zealand Solar Energy Society, September 13-13, 2006, Canberra, Australia.[2011-11-12]. http://solar-thermal.anu.edu.au/files/2010/02/Paitoonsurikarn2Sol06.pdf . |
| [7] | Bilgen E. Passive solar massive wall systems with fins attached on the heated wall and without glazing[J]. Journal of Solar Energy Engineering, 2000, 122(1): 30–34. DOI:10.1115/1.556274 |
| [8] | Abanades S, Charvin P, Flamant G. Design and simulation of a solar chemical reactor for the thermal reduction of metal oxides:case study of zinc oxide dissociation[J]. Chemical Engineering Science, 2007, 62(22): 6323–6333. DOI:10.1016/j.ces.2007.07.042 |
| [9] | Wang M, Siddiqui K. The impact of geometrical parameters on the thermal performance of a solar receiver of dish-type concentrated solar energy system[J]. Renewable Energy, 2010, 35(11): 2501–2513. DOI:10.1016/j.renene.2010.03.021 |
| [10] | Chakroun W. Effect of boundary wall conditions on heat transfer for fully opened tilted cavity[J]. ASME Journal of Heat Transfer, 2004, 126(6): 915–923. DOI:10.1115/1.1798931 |
| [11] |
刘志刚, 张春平, 赵耀华, 等.
一种新型腔式吸热器的设计与实验研究[J]. 太阳能学报, 2005, 26(3): 332–337.
LIU Zhigang, ZHANG Chunping, ZHAO Yaohua, et al. The design and experiments of a new cavity absorber[J]. Acta Energiae Solaris Sinica, 2005, 26(3): 332–337. (in Chinese) |
| [12] | Umarov I, Fattakhov A, Umarov A, et al. Heat loss in a cavity-type solar collector[J]. Applied Solar Energy, 1983, 19(3): 35–38. |
| [13] | Reddy K S, Kumar N S. Combined laminar natural convection and surface radiation heat transfer in a modi? ed cavity receiver of solar parabolic dish[J]. International Journal of Thermal Sciences, 2008, 47(12): 1647–1657. DOI:10.1016/j.ijthermalsci.2007.12.001 |
| [14] | Hinojosa J F, Cabanillas R E, Alvarez G, et al. Nusselt number for the natural convection and surface thermal radiation in a square tilted open cavity[J]. International Communications in Heat and Mass Transfer, 2005, 32(9): 1184–1192. DOI:10.1016/j.icheatmasstransfer.2005.05.007 |
 2013, Vol. 36
2013, Vol. 36

