眼压即眼内压(Intraocular pressure,IOP),是眼球内部的压力。眼压的大小是医生判断眼睛健康的重要标志,也是诊断和治疗青光眼的重要依据,其测量值是否能准确反应眼内压力的“真实”值,直接关系到青光眼的早期诊断水平,为此,许多国家开展了对眼压测量技术的研究工作[1]。
非接触眼压测量是近年来出现的一种新型的眼压测量技术,与传统的接触式眼压测量技术相比,其测量时不需与眼膜直接接触、无需麻醉、不会产生交叉感染,具有安全、卫生、无痛苦等特点。
目前,国外出现的非接触眼压计主要有:利用脉冲气流代替外加机械压力将眼膜压平到一定面积,根据压平所需时间、压平面积、气流大小和眼内压之间的关系得出眼压值的压平式眼压计[2-8],以及利用气流脉冲或声脉冲撞击眼膜引发眼膜振动,从而通过测量振动程度与眼内压的关系来测量眼压的非接触式眼压计[9-10]。这2种测量技术在国外已经相对比较成熟,但仪器设备复杂,造价昂贵,技术条件要求高(需要进行定期标定)[11-12]。此外,由于国外专利技术的保护,国内至今无法生产和普及非接触眼压计。
参考文献[13]中提出了一种采用激光干涉检测代替光电检测或超声检测的激光干涉式非接触眼压测量方法,尽管可以严格控制激光的功率,但对眼角膜采用激光检测仍具有一定的风险性,故从提出至今该系统并未实用化。
鉴于上述非接触眼压测量技术的优缺点,提出了一种基于力平衡原理和空气静压技术的新型非接触式眼压测量方法,实现了眼压的非接触测量,使病人无痛苦,不需眼角膜有较大形变,同时又具有造价低、使用方便、体积小等特点。
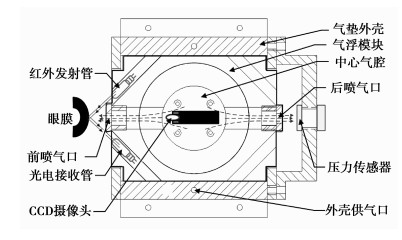
1 基本工作原理 1.1 气浮测量装置原理笔者提出的眼压测量方法与目前国内外其他类型的非接触测量方法在原理上有很大的差别,具体原理是:结合力平衡原理和空气静压技术设计气浮式眼压测量装置(如图 1所示),当供气系统对气浮式眼压测量装置的气垫外壳供气时,气垫外壳与气浮测量模块之间产生一层气膜,气浮测量模块悬浮于气垫外壳内不受固体摩擦力的作用(气体摩擦力可忽略不计),处于力平衡状态。此时,气浮式眼压测量模块前侧喷嘴的气流将眼膜喷平的压力和后侧喷嘴气流喷至压力传感器产生的作用力相平衡,由于眼膜到前侧喷嘴的距离与压力传感器到后侧喷嘴的距离相等,眼膜被喷平时,通过传感器测得的压力即为眼内压值。
|
图 1 气浮测量装置结构图(俯视) |
在喷气过程中利用CCD摄像头实时监测眼膜,使眼膜中央位于前侧喷气口的正中。喷气口的两侧分别有一红外发射管和光电接收管,喷气时,发射管向眼膜发射红外光,经眼膜反射后被接收管接收,通过检测光电接收管接收到红外光信号的大小来判断眼膜是否被喷平。
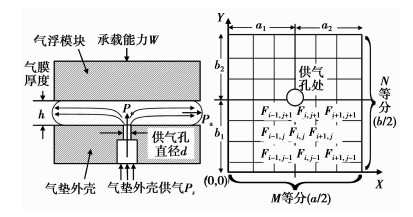
1.2 空气静压气垫设计测量装置采用外框式气浮垫结构进行设计,外框式气浮垫的左、右气浮面和底部气浮面均采用小孔节流式静压止推气体轴承结构。由于每个轴承面上均有4个对称配置的节流孔,所以可根据其分布特性对轴承面的1/4进行研究,采用有限元计算方法精确计算空气轴承内气膜压力的分布情况和静态特性[14-15]。图 2所示为1/4气体轴承结构原理图,主要由具有节流孔的气垫外壳和作为载荷的气浮模块组成。压力为Ps的压缩空气经节流孔进入气膜间隙,压力降为Po后沿支撑面流至轴承两端排入大气,从而在气垫外壳和气浮模块之间造成一定的压力分布,使气浮模块处于悬浮状态。
|
图 2 空气静压气垫轴承结构及网格划分 |
假设气膜厚度h一定,气膜内气体的流动是等温流、定常状态,以轴承面的长为x轴,宽为y轴设置坐标(如图 2所示),则有雷洛方程式
| $ \frac{{{\partial ^2}{p^2}}}{{{\partial ^2}{x^2}}} + \frac{{{\partial ^2}{p^2}}}{{{\partial ^2}{y^2}}} = 0。$ | (1) |
由于x=0、y=0处与大气压相接,x=a/2、y=b/2处气压沿x轴、y轴变化为0,则有边界条件
| $ \left. \begin{align} &x=0\ 时\ \ p={{p}_{a}}, x=a/2\ \ \ 时\ \ \frac{\partial p}{\partial x}=0\ \ \ \ \ \\ &y=0\ 时\ \ p={{p}_{a}}, y=b/2\ \ \ 时\ \ \frac{\partial p}{\partial y}=0 \\ \end{align} \right\}。$ | (2) |
其中:a、b分别为整个轴承面的长和宽。
为了实现数字计算,用垂直于x轴和y轴的直线将轴承面等分成M等分和N等分,成为网格状(如图 2所示),在x轴上用i计数,y轴方向上用j计数,节点(i,j)上的压力值p2设为Fi,j,则根据差分法(1)式可表示为[15]
| $ {{F}_{i, j}}= \frac{1}{T}\left\{ \frac{1}{\Delta {{x}^{2}}}({{F}_{i+1, j}}+{{F}_{i-1, j}})+\frac{1}{\Delta {{y}^{2}}}({{F}_{i, j+1}}+{{F}_{i, j-1}}) \right\}。$ | (3) |
与此对应,式(2)边界条件可表示如下
| $ \left. \begin{align} &F\left( 0, 0 \right)=P_{a}^{2} \\ &F\left( \frac{a}{2}, y \right)=\frac{1}{T}\left\{ \frac{1}{\Delta {{x}^{2}}}\cdot 2{{F}_{i-1, j}}+\frac{1}{\Delta {{y}^{2}}}({{F}_{i, j}}+{{F}_{i, j-1}}) \right\} \\ &F\left( x, \frac{b}{2} \right)=\frac{1}{T}\left\{ \frac{1}{\Delta {{x}^{2}}}({{F}_{i+1, j}}+{{F}_{i-1, j}})+\frac{1}{\Delta {{y}^{2}}}\cdot 2{{F}_{i, j-1}} \right\} \\ &F\left( \frac{a}{2}, \frac{a}{2} \right)=\frac{1}{T}\left\{ \frac{1}{\Delta {{x}^{2}}}\cdot 2{{F}_{i-1, j}}+\frac{1}{\Delta {{y}^{2}}}\cdot 2{{F}_{i, j-1}} \right\} \\ &F\left( 0, y \right)=F\left( x, 0 \right)=p_{a}^{2} \\ &F\left( {{a}_{1}}, {{b}_{1}} \right)=p_{a}^{2} \\ \end{align} \right\},$ | (4) |
式中,
根据式(3)、(4),以Fi,j=1(Fa1,b1点除外)为初始条件,利用加速利普曼法(逐步超松弛法)反复进行计算,直到满足以下收敛条件:
| $ \frac{\sum\limits_{i=0}^{M-1}{\sum\limits_{j=0}^{N-1}{\left| \overline{F_{i, j}^{(r+1)}}-\overline{F_{i, j}^{(r)}} \right|}}}{\sum\limits_{i=0}^{M-1}{\sum\limits_{j=0}^{N-1}{\left| \overline{F_{i, j}^{(r+1)}} \right|}}}\leqslant \sigma。$ | (5) |
由此,可计算出对应于供气孔出口压力Po的压力分布。式(5)中Fi,j(r)表示节点(i,j)上第r次计算的值,而
计算出压力分布后,首先求x方向压力分布的积分值PWj,再用PWj值对y方向上积分,采用辛普松公式求出承载能力W,如式(6)所示。
| $ \left. \begin{align} &P{{W}_{j}}=\frac{\Delta x}{3}\sum\limits_{i=0, 2, \cdots }^{M-1}{\{\left( {{P}_{i, j}}-{{P}_{a}} \right)}+ \\ &4\left( {{P}_{{i+1},j}}-{{P}_{a}} \right)+\left( {{P}_{i+2, j}}-{{P}_{a}} \right)\}, \\ &W=\frac{\Delta y}{3}\sum\limits_{j=0, 2\cdots }^{N-2}{\left( P{{W}_{j}}+4P{{W}_{j+1}}+P{{W}_{j+2}} \right)}。\\ \end{align} \right\} $ | (6) |
对于图 2所示轴承,假设通过单个供气孔流入轴承的气体流量为Win,则
| $ {{W}_{\text{in}}}=\pi \text{d}h{{C}_{0}}\psi \cdot \frac{{{P}_{\text{s}}}}{\sqrt{R{{T}_{0}}}}。$ | (7) |
而由轴承周围流出的气体流量Wout为
| $ \begin{align} &{{W}_{\text{out}}}=\frac{{{h}^{3}}}{12\mu }\{\sum\limits_{i=0}^{M-1}{\frac{\left| {{P}_{i, 2}}-{{P}_{i, 0}} \right|{{P}_{i, 1}}\cdot \Delta x}{2\cdot \Delta y}}+ \\ &\ \ \ \ \ \ \sum\limits_{j=0}^{N-1}{\frac{\left| {{P}_{2, j}}-{{P}_{0, j}} \right|{{P}_{1, i}}\cdot \Delta y}{2\cdot \Delta x}}\}{{\gamma }_{a}}。\\ \end{align} $ | (8) |
由于Win=Wout,根据此关系式可计算出气膜厚度h。式中:C0、ψ、R、T0、μ、γa分别表示供气孔喷嘴的流量系数、流出速度系数、气体常数、温度、动力粘度和气体密度。
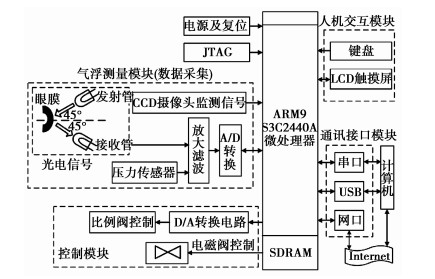
2 系统总体结构设计图 3所示为系统总体结构图,该系统主要由以下模块组成:ARM9微处理器模块、气浮测量模块、控制模块、人机交互及通讯接口模块等。
|
图 3 系统总体结构图 |
系统以ARM9系列的S3C2440A为核心处理器。其中控制系统主要是通过调节比例阀和电磁阀,完成对气浮测量装置中心气腔的供气。气浮测量模块主要完成数据的采集,其中CCD摄像头实时检测瞳孔位置,压力传感器采集后喷嘴喷气压力,光电检测模块采集眼膜反射光信号。此外,基于ARM9丰富的I/O功能,还设计了外围电路,扩展相应的功能模块,包括键盘、LCD触摸屏、USB口,串口和网口通讯等。
3 硬件系统设计 3.1 气路系统供气系统采用TP551F1型便携式静音无油空压机作为供气装置,功率550 W,最高压力8 Pa,排量最高可达118 L/min,具有噪声小、使用方便、经济实惠的特点。
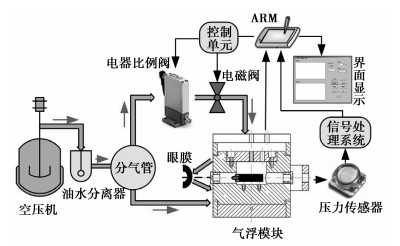
图 4所示为总体的硬件实现:系统通过空压机将气体压缩到设定压强,并存储在气罐中,再经气管进入油水分离器进行油水过滤,干燥后由分气管将其分为两路,其中一路直接给气浮测量装置的气垫外壳供气,用于产生一定厚度的气膜,使气浮测量模块悬浮在气垫外壳内处于平衡状态;另外一路经电气比例阀和电磁阀开关后给气浮测量模块的中心气腔供气,用于喷平眼膜及气压传感器实时检测。
|
图 4 总体硬件结构 |
系统采用微型USB CCD摄像头对瞳孔图像进行实时检测,有30万像素和640×480的分辨率。摄像头整体尺寸8 mm×28 mm,镜头直径8 mm,位于气浮测量模块气腔的中央。摄像头镜头正对前喷气口,可对测试者瞳孔进行实时监测,同时在LCD屏上显示瞳孔图像,测试眼压时,需调节眼睛位置使瞳孔正对前喷气口正中。此外,在摄像头镜头的左右两边对称位置,分别有一个LED灯,主要用于人眼的固视。
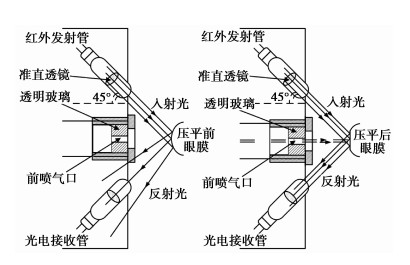
3.3 光电检测系统如图 5所示为光电检测示意图,该检测系统主要由红外发射管、光电接收管和准直透镜组成。发射管和接收管位于气浮测量模块前喷气口两端对称位置,成额定45°角倾斜瞄准被测者角膜顶点,且分别位于准直透镜的焦距上。当角膜与前喷气口位置达到额定距离时,控制系统提升中心气腔的供气压力,光电检测系统开始工作。随着供气压力的增强,从前喷气口喷出的气体使眼角膜变形,此时从光电发射管发射的红外光经透镜准直后射向角膜,再经角膜反射后,又通过透镜会聚到光电接收管接收。当被测角膜被压平时,光电接收管接收到的光强达到最大值。
|
图 5 光电检测示意图 |
由于系统对动态特性的要求较高,同时压力测量的量程范围较小,因此压力传感器的选取极为重要,考虑到分辨率、采样率和动态性能等因素,选取迈姆斯公司的MPS20N0100A-P作为系统压力测量传感器。该传感器是一款PCB模块封装模拟压力传感器,被广泛应用于测量气压、水压等无腐蚀性流体,具有良好的可重复性和长时间的工作稳定性。其外围尺寸6.9 mm×6.3 mm,易于系统集成。
传感器输出的模拟信号经过由AD620组成的差分放大电路后,经过A/D转换器将压力传感器信号转换为数字量,输入到微处理器做进一步的处理。
3.5 微处理器模块现有的非接触式眼压测量装置大都采用单片机控制,功能简单。为了提高系统性能,采用基于ARM920T内核的32位嵌入式微处理器S3C2440A作为CPU,其配置的2片32M SDRAM,1片64M NAND flash,2片16位SDRAM器件共同组成一个32位数据宽度的SDRAM系统,提高了与CPU通信效率,更好地实现了系统性能。
人机交互模块采用TFT-LCD搭配触摸屏设计,在LCD上可对测量控制参数进行设定,在测量结束后绘制压力曲线和光电接收曲线,并计算出最终测出的眼压值。
4 软件系统设计系统选用ARM-Linux和QT作为开发平台,与其他的嵌入式操作系统WinCE、Vxworks、pSoS相比,Linux可以适应多种体系结构,具有性能稳定、可裁剪性好、开源等特点。
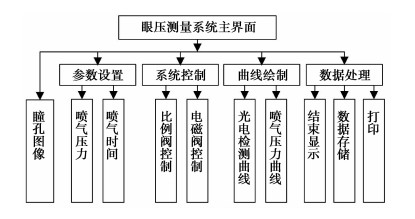
基于Linux系统,可以通过设计驱动程序、API函数等实现内核的移植和扩展。利用QT开发平台,完成眼压测量系统软件设计,实现眼压测量过程的控制、数据采集与分析处理、光电检测信号和压力信号的曲线绘制,以及测量数据显示和储存等,软件系统框图如图 6所示。
|
图 6 软件系统框图 |
设计的气垫采用小孔节流,节流小孔直径d=0.2 mm,4个节流小孔均布在气垫平面上。节流小孔喷嘴采用人造红宝石制造,人造红宝石具有硬度高,加工性能好的优点。采用激光打孔和研磨后,制造的人造红宝石节流小孔的直径误差±0.015 mm。
将气浮测量模块置于气垫外壳内,调节压力供气装置为气垫外壳供气,则气浮测量模块由于受到底面和侧面气浮气垫的支撑而悬浮,与外壳之间产生一定的气膜厚度,可根据气膜厚度、供气压力、气浮测量模块质量之间的关系分析气浮式眼压测量装置的气浮特性。
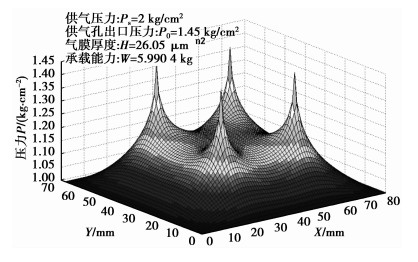
图 7所示气垫外壳供气压力Ps=2 kg/cm2,气膜厚度h=26.05 μm时,气浮测量模块与底部气垫外壳间的气体压力分布,气体压力从供气孔处开始沿支撑面向四周逐渐降低,至外壳边缘与大气压相近。由于4个供气孔对称分布,气浮测量模块与气垫外壳间的气体压力分布也相应对称,气膜厚度处处相等。此外,在Ps=2 kg/cm2,h=26.05 μm处供气孔出口压力P0=1.45 kg/cm2,有5.99 kg的承载能力,完全可以使气浮测量模块处于悬浮状态。
|
图 7 气浮模块与气垫外壳间的气体压力分布 |
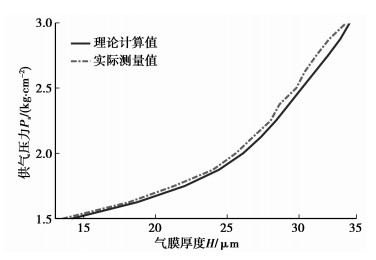
图 8所示为气浮测量模块质量固定时,气垫外壳供气压力Ps与气膜厚度h的关系曲线。由实验曲线可见,在气浮测量模块质量固定时,增加供气压力,气膜厚度相应增大,且只需1.5 kg/cm2的供气压力,气膜厚度就可达到15 μm左右,即气浮测量模块能正常悬浮于外壳内,达到了设计目的。图中实线为理论分析值,虚线为利用光栅测头传感器在不同供气压力下测得的气膜厚度实际值,通过对比,在一定的供气压力下,实际的气膜厚度与理论气膜厚度几乎相等。
|
图 8 供气压力与气膜厚度关系曲线 |
在密闭条件下用压力传感器测量供气的压强,通过电器比例阀调节对密闭环境的供气压力大小,在无气体泄漏的情况下对压力传感器的静态性能进行标定。
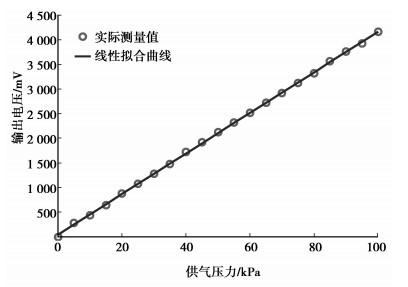
根据压力传感器的量程,测试在供气压力每次增加5 kPa的情况下,经放大滤波、A/D转换后的压力传感器输出信号值。对标定的结果进行线性拟合处理,结果如图 9所示,由曲线图可以看出,压力传感器的输出与供气压力之间有良好的线性关系,供气压力每升高1 kPa,压力传感器输出电压变化41.164 mV。
|
图 9 压力传感器标定曲线 |
由于压力传感器检测到的实际喷气压力与中心气腔供气压力不同,在仪器系统调试时,需要通过调节中心气腔的供气压力,测试喷嘴实际喷出气体压力,保证其在常用眼压范围内。由于眼膜到前侧喷嘴的距离与压力传感器到后侧喷嘴的距离相等,所以实验时只需要测试压力传感器处的实际喷气压力与中心气腔供气压力之间的关系,以便确定进行非接触眼压测量时中心气腔所需的供气压力。
由实验结果确定,气浮测量模块中心气腔供气压力在300 kPa左右时,压力传感器处喷气压力达到常用的眼压范围。
图 10所示为设计的非接触式眼压测量装置图,被测者坐在测量装置台前,下巴位于托架上,检测者通过显示屏观察瞳孔图像,利用手柄前后、左右调节测量装置,使瞳孔对准气浮测量模块前喷气口正中,同时根据图像的大小和清晰度判断眼膜与前喷气口之间的距离,当图像最清晰时,达到额定距离,然后对眼压进行测量。

|
图 10 非接触式眼压测量装置图 |
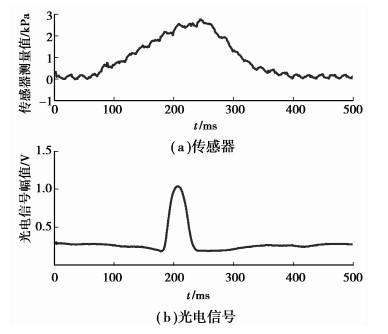
图 11所示为实际眼压测量时绘制的喷气压力曲线和光电信号曲线,根据压平眼膜过程中反射光量的关系,眼膜压平时反射光最强,此时传感器测得的压力值即为需要测量的眼压值。图中光电信号最大值对应压力2.52 kPa,换算为常用单位表示测得的眼压为18.5 mmHg。
|
图 11 眼压测量时光电信号与传感器测量曲线 |
为了检验测量装置的准确性,利用医院进口非接触式眼压计(Canon TX-F)和设计的眼压测量系统进行对比实验。表 1所示是对4个志愿者进行对比测试的结果,即在相同环境下,用2种仪器分别对同一对象连续测量3次,计算眼压平均值、重复性和相对误差。
| 表 1 对比测试实验数据 |
由表 1所示,在相同环境下,利用国外进口眼压计测量眼压的重复性误差≤5.09%,而装置测量眼压的重复性误差≤6.01%,虽然重复性误差略大于进口仪器,但仍然表明测量装置具有较高的稳定性。而与进口仪器相比眼压测量平均值的绝对误差≤1.3 mmHg,说明研究设计的眼压测量装置可以对眼压进行较准确的测量,验证了采用空气静压技术和力平衡原理进行非接触眼压测量的可行性。
相对于国外进口仪器,装置测量眼压的重复性误差偏大,据分析这是由于采用的CCD摄像头景深偏大,在前喷气口与眼膜之间的距离有较小变化时,通过瞳孔图像清晰度不能对其进行分辨,产生了一定的误差。在后续研究中,考虑设计景深较小更符合要求的摄像头成像物镜,以提高测量精度。
6 结语提出并设计了一种基于力平衡原理和空气静压技术的非接触眼压测量系统,即在力平衡条件下通过测量与眼角膜受力相同的传感器压力而直接得出眼压值,该设计思想和仪器结构设计与现有的根据气体脉冲持续时间和气腔内压关系测量眼压完全不同,结构简单,测量方便,具有创新性和实用性。该非接触眼压测量系统具有自主知识产权,为我国自主生产非接触眼压计提供了一定技术支持。
| [1] |
干江红, 周莉萍, 徐龙.
眼内压力测量技术的研究[J]. 中国医疗器械杂志, 2009, 33(3): 202–206.
GAN Jianghong, ZHOU Liping, XU Long. The study on techniques for monitoring intraocular pressure[J]. Chinese Journal of Medical Instrumentation, 2009, 33(3): 202–206. (in Chinese) |
| [2] | Kanngiesser H E, Kniestedt C, Robert Y C. Dynamic contour tonometry:presentation of a new tonometer[J]. Journal of Glaucoma, 2005, 14(5): 344–350. DOI:10.1097/01.ijg.0000176936.16015.4e |
| [3] | Lam A K, Chan R, Lam C H. The validity of a new noncontact tonometer and its comparison with the Goldmannn tonometer[J]. Optometry and Vision Science, 2004, 81(8): 601–605. DOI:10.1097/01.opx.0000141796.95597.43 |
| [4] | Pepose J S, Feigenbaum S K, Qazi M A, et al. Changes in corneal biomechanics and intraocular pressure following LASIK using static, dynamic and noncontact tonometry[J]. American Journal of Ophthalmology, 2007, 143(1): 39–47. DOI:10.1016/j.ajo.2006.09.036 |
| [5] | Lam A, Chen D, Chiu R, et al. Comparison of IOP measurements between ORA and GAT in normal Chinese[J]. Optometry and Vision Science, 2007, 84(9): 909–914. DOI:10.1097/OPX.0b013e3181559db2 |
| [6] | Kempf R, Kurita Y, Lida Y, et al. Understanding eye deformation in non-contact tonometry[C]//Proceedings of the 28th Annual International Conference of the IEEE Engineering Medicine and Biology Society, August 30-September 3, 2006, New York, NY. Piscataway:IEEE Press, 2006, 1:5428-5431. |
| [7] | Han Y M, Bryanston-Cross P J, Lee W K, et al. Active non-contact tonometer for glaucoma detection[J]. Optics in Health Care and Biomedical Optics:Diagnostics and Treatment, 2002, 4916: 143–150. DOI:10.1117/12.482946 |
| [8] | Ogbuehi K C, Almubrad T M. Accuracy and reliability of the Keeler Pulsair EasyEye non-contact tonometer[J]. Optometry and Vision Science, 2008, 85(1): 61–66. DOI:10.1097/OPX.0b013e31815ed742 |
| [9] | Gloster J, Perkins E S. The validity of the imbert-fick law as applied to applanation tonometry[J]. Experimental Eye Research, 1963, 2(3): 274–283. DOI:10.1016/S0014-4835(63)80048-2 |
| [10] | Hsu H. Non-contact high frequency tonmeter:US, 4928697 A[P]. 1990-05-29. |
| [11] |
祝远方, 郭文毅.
新型非接触式眼压分析仪ORA与Goldmann压平眼压计的比较[J]. 中国实用眼科杂志, 2007, 25(5): 521–523.
ZHU Yuanfang, GUO Wenyi. The comparison of intraocular pressure measurement between ocular response analyzer and Goldmann applanation tonometer[J]. Chinese Journal of Practical Ophthalmology, 2007, 25(5): 521–523. (in Chinese) |
| [12] |
张学勇, 马建国, 卢荣胜.
眼压检测技术应用研究[J]. 合肥工业大学学报:自然科学版, 2011, 34(7): 976–981.
ZHANG Xueyong, MA Jianguo, LU Rongsheng. State of arts of intraocular pressure measurement technology[J]. Journal of Hefei University of Technology:Natural Science, 2011, 34(7): 976–981. (in Chinese) |
| [13] | 李玉峰. 激光干涉式非接触眼压计中电信号处理与控制系统研究[D]. 天津: 天津大学硕士学位论文, 2004. http://d.wanfangdata.com.cn/Thesis/Y592515 |
| [14] |
黄灏, 刘品宽, 董泽光.
静压止推气体轴承性能仿真[J]. 计算机仿真, 2010, 27(3): 340–343, 361.
HUANG Hao, LIU Pinkuan, DONG Zeguang. The performances simulation of aerostatic thrust bearing[J]. Computer Simulation, 2010, 27(3): 340–343, 361. (in Chinese) |
| [15] | 十合晋一. 气体轴承设计、制作与应用[M]. 韩焕臣, 译. 北京: 宇航出版社, 1988. |
 2013, Vol. 36
2013, Vol. 36

