2. 中国大唐集团科学技术研究院, 北京 100032
2. China Datang Corporation Science and Technology Research Institute, Beijing 100032, China
现今一次能源日益紧张,传统燃煤火电机组面临着诸多新型发电模式迅猛发展所带来的巨大竞争压力。而且,燃煤机组因电厂燃料的供应渠道不稳定,面临热值多变且煤质更差的现状[1]。另外,并网机组承担电网一次调频的任务,机组面临频繁负荷波动。兼顾快速性和准确性的机组燃水比(Firing rate to feed water ratio,FR/FW)调节反馈信号精确检测依然困难,制约燃水比控制[2-4]。
变工况时,机组结构和参数时变,纯迟延部分变化较大。基于额定工况下设计的固定参数PID控制器自适应能力及鲁棒性差[5-6],常常引起燃料量或给水量调节过量,使锅炉远偏离于设计工况运行,进而危害机组运行安全。文献[7-8]分别基于Smith预估控制和内模控制的现代控制理论方法来优化燃水比控制,但其建模过程依赖精确对象数学模型,限制实际应用效果。在分析某厂600 MW超临界机组燃水比控制系统存在的局限性后,将具备较好非线性逼近能力、快速并行处理能力和自学习能力的动态递归模糊神经网络[9-16]应用于超临界机组燃水比控制系统中,而固定拓扑结构神经网络在信息处理时不能充分发挥其性能,提出一种基于生长-剪枝动态递归模糊神经网络的燃水比控制方法,实时改变网络神经元个数及神经网络拓扑结构。随当前相关状态参数输入,GAP-DRFNN自动增加和修剪神经元,且依据梯度下降法,动态调整网络的隶属函数参数及神经网络递归权值,极大改善变工况下控制系统抗扰动及适应非线性的能力。GAP-DRFNN以汽水分离器出口工质温度偏差最小为导师信号,综合与燃水比相关的主要状态参数,如:末级和中间级过热器出口温度、汽水分离器出口汽温等,并依据当前汽温控制设定,实时运算出最佳FR/FW。试验对比表明该优化方案在机组燃水比控制及运行上的可行性。
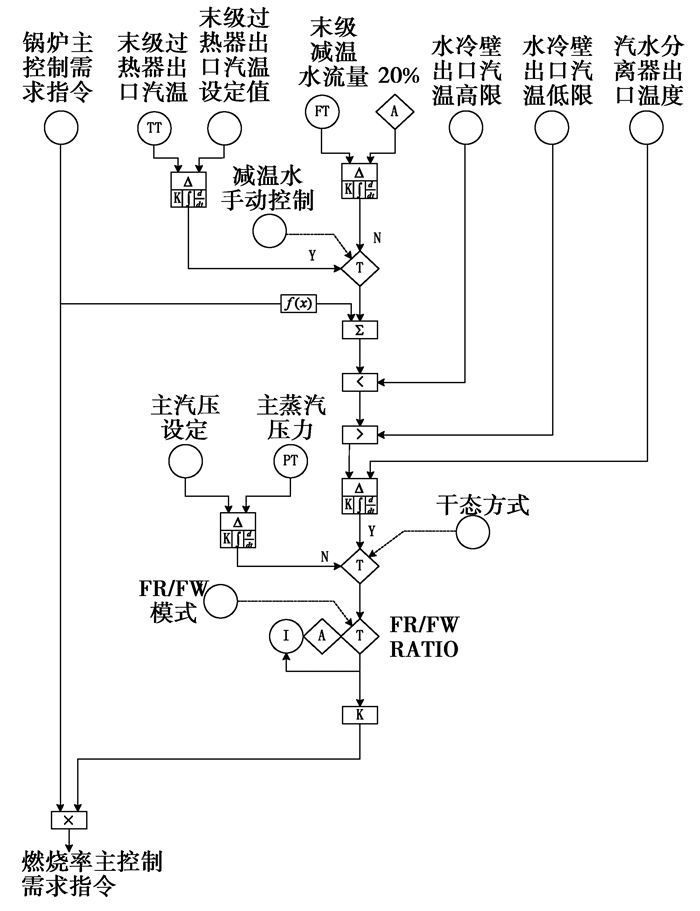
1 超临界机组燃水比控制特性及问题分析如图 1所示为某厂600 MW超临界机组在干态模式下燃水比控制系统。
|
图 1 燃水比控制原理图 |
该燃水比以汽水分离器出口蒸汽温度为控制目标。汽水分离器出口温度设定值是锅炉主控需求指令的函数关系,其测量值作为控制的反馈,两者差值经PID主控制器运算之后得出FR/FW,并用于修正燃烧率控制指令。此控制方案设置了汽水分离器出口温度的设定值高低限,以免水冷壁受热面管材因高温疲劳或温度过低而危害汽水循环的动力特性。此外,以减温水流量及末级过热器蒸汽温度为锅炉燃水比的前馈控制,减温水流量或过热蒸汽温度发生变化时,FR/FW及时变化,且FR/FW通过快速修正燃烧率控制指令调整燃料量。
此燃水比控制系统,利用有限锅炉运行工况参数,仅有汽水分离器出口温度、末级过热器汽温以及减温水流量,未有效利用过热器导前汽温等,不足以全面反映锅炉运行工况变化,尤其热量在锅炉各实际受热面的分布情况。因而,难以计算出精确的FR/FW。此外,因干扰因素较多,有时并不能精确测量出减温水流量,若将其引入燃水比控制,喷水量过多,系统火用损失增大,再则势必带来扰动,不利于工况稳定。此FR/FW使用传统PID线性控制器,克服直流锅炉过热汽温及燃烧控制对象的强非线性并对其解耦能力较差,变工况控制时尤其明显。
2 燃水比GAP-DRFNN优化控制设计燃水比控制以保证锅炉汽水分离器出口汽温在设定值为目标。为此,输入量分别为能够反映控制过程中过热汽温粗调节效果的末级过热器出口汽温与主蒸汽温度给定值之差值η(t);表征减温水投入当量,以排除其流量测量诸多干扰因素,并减少与减温喷水控制耦合作用的减温水导前汽温偏差z(t);汽水分离器出口工质温度y(t)、设定值r(t)。此控制系统,y(t)作为系统反馈控制量,减温器前后汽温与主汽温为系统前馈,FR/FW控制滞后效应大为减小。因此,GAP-DRFNN输入量为
| $ \begin{array}{l} \mathit{\boldsymbol{x}} = {\left[ {{x_1},{x_2},{x_3},{x_4}} \right]^{\rm{T}}} = \\ \;\;\;\;\;\;{\left[ {y\left( t \right),z\left( t \right),\eta \left( t \right),r\left( t \right)} \right]^{\rm{T}}}。\end{array} $ | (1) |
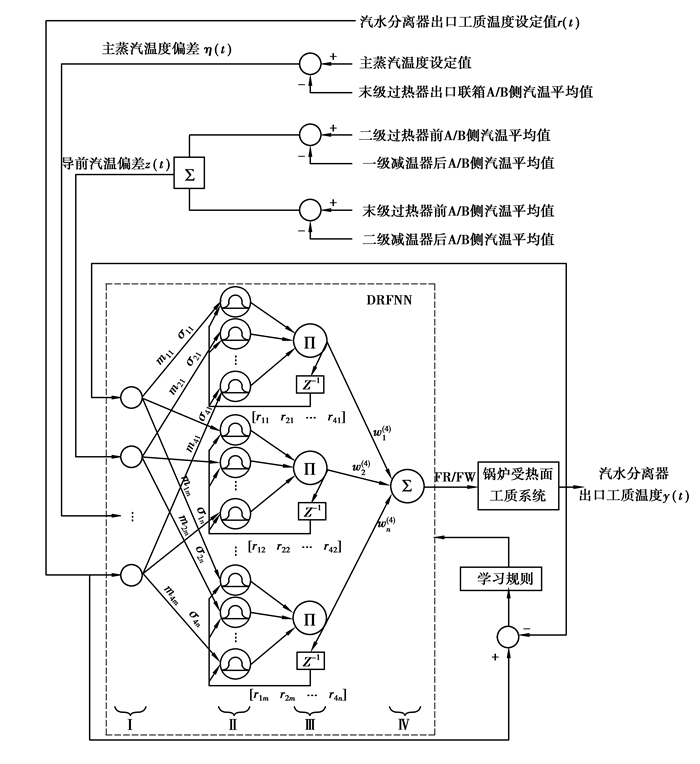
四输入单输出GAP-DRFNN优化控制系统结构如图 2所示。
|
图 2 燃水比GAP-DRFNN优化控制系统 |
第Ⅰ层:输入层。
| $ \left. \begin{array}{l} net_i^{\left( 1 \right)} = x_i^{\left( 1 \right)}\\ y_i^{\left( 1 \right)} = f_i^{\left( 1 \right)}\left( {net_i^{\left( 1 \right)}} \right) = net_i^{\left( 1 \right)}\\ i = 1,2, \cdots ,4 \end{array} \right\}, $ | (2) |
式中,xi(1)代表网络输入量。
第Ⅱ层:模糊化层。该层将输入变量模糊化,采用的模糊隶属函数为高斯基函数。
| $ \left. \begin{array}{l} net_{ij}^{\left( 2 \right)} = - \left\{ {{{\left[ {x_i^{\left( 2 \right)} - {m_{ij}} - {r_{ij}} \cdot y_{jp}^{\left( 3 \right)}} \right]}^2}/{{\left( {{\sigma _{ij}}} \right)}^2}} \right\}\\ y_{ij}^{\left( 2 \right)} = {f^{\left( 2 \right)}}\left( {net_{ij}^{\left( 2 \right)}} \right) = \exp \left( {net_{ij}^{\left( 2 \right)}} \right)\\ j = 1,2, \cdots ,n \end{array} \right\}, $ | (3) |
式中:xi(2)为第Ⅱ层的第i个输入;mij、σij分别表示高斯基函数的均值中心和标准偏差;rij是模糊规则的反馈增益;yjp(3)是第Ⅲ层前一次迭代输出对第Ⅱ层第j个节点的作用;n表示输入节点相应的全部语言变量数。模糊化层输入信号为该层当前输入和第Ⅲ层节点输出加权信号的延迟。因此,第Ⅱ层输出不仅受当前输入影响,而且网络过去的输出信息对其也有影响。
第Ⅲ层:推理层。此层各节点k用Π表示,即输入信号的乘积为输出结果。
| $ \left. \begin{array}{l} net_k^{\left( 3 \right)} = \prod {w_{jk}^{\left( 3 \right)}x_j^{\left( 3 \right)}} \\ y_k^{\left( 3 \right)} = f_k^{\left( 3 \right)}\left( {net_k^{\left( 3 \right)}} \right) = net_k^{\left( 3 \right)}\\ k = 1,2, \cdots ,n \end{array} \right\}, $ | (4) |
式中:xj(3)表示第Ⅲ层第j个输入;wjk(3)为模糊化层与推理层之间的权值,且均取值为1。
第Ⅳ层:输出层。该层仅有一个节点O,所有输入信号之和即为去模糊化输出结果。
| $ \left. {\begin{array}{*{20}{l}} {net_o^{\left( 4 \right)} = \sum\limits_k {w_{ko}^{\left( 4 \right)}x_k^{\left( 4 \right)}} }\\ {y_o^{\left( 4 \right)} = f_o^{\left( 4 \right)}\left( {net_o^{\left( 4 \right)}} \right) = net_o^{\left( 4 \right)}}\\ {o = 1} \end{array}} \right\}, $ | (5) |
式中:xk(4)为第Ⅳ层输入量;输出节点与第k条规则的连接权值wko(4)初值为0,其值动态自适应学习调整;yo(4)=u(t)为GAP-DRFNN控制器的输出量,即为燃水比控制量FR/FW。
3 燃水比GAP-DRFNN优化控制算法 3.1 GAP-DRFNN结构学习算法GAP-DRFNN分为结构学习和参数学习,合适的网络结构学习方案包括节点的生长和剪枝[17-20]。在节点的生长过程中,任一输入数据xi(1)隶属于模糊规则的适用度由式(4)知
| $ {\beta _k} = y_k^{\left( 3 \right)},k = 1,2, \cdots ,n。$ | (6) |
定义最大适用度值为βmax,
| $ \begin{array}{l} \sigma _i^{{\rm{new}}} = x_i^{\left( 1 \right)},\sigma _i^{{\rm{new}}} = \bar \sigma ,\\ {r^{{\rm{new}}}} = 0,w_i^{{\rm{new}}} = 0, \end{array} $ | (7) |
其中:xi是新输入信号;σ是预先设定常量。当控制系统动态特性复杂,需要更多模糊规则时,βth可以选取1个较大值,增加更多神经元,反之亦然。
神经网络需要修剪多余的节点,确保每一个节点都能够很好的激活。第k个节点的重要性表示为
| $ {I_k}\left( {N + 1} \right) = {I_k}\left( N \right)\exp \left[ { - \tau \times {\mu _{\rm{s}}}\left( {\rho ,{\beta _k}} \right)} \right], $ | (8) |
其中:Ik(N)是衡量第k个节点在第N个采样时刻的显著因子,初始值设为1;ρ是预先设定的阈值,用来删除现有节点;τ表示消除速率的常量;μs是单位阶跃函数。
| $ {\mu _{\rm{s}}}\left( {\rho ,{\beta _k}} \right) = \left\{ \begin{array}{l} 1,{\rm{if}}\;\;\;\left( {\rho - {\beta _k}} \right) \ge 0,\\ 0,{\rm{if}}\;\;\;\left( {\rho - {\beta _k}} \right) < 0。\end{array} \right. $ | (9) |
如果第k条规则经过一段时间不能很好的激活,则认为此节点对于DRFNN不重要,即当Ik≤Ith时,第k条规则从DRFNN中修剪,Ith是预先设定的常量。同理Ith选取一个较小值,可以保留更多神经元。
3.2 GAP-DRFNN参数学习算法依据梯度下降法[21]训练学习GAP-DRFNN的隶属函数参数mij、σij以及神经网络递归权值wko、rij。定义控制系统瞬时误差代价函数为
| $ J\left( n \right) = {e^2}\left( n \right)/2 = {\left[ {r\left( t \right) - y\left( t \right)} \right]^2}/2。$ | (10) |
连接权值wko变化率为
| $ \begin{array}{*{20}{c}} {\Delta {w_{ko}}\left( n \right) = - \eta \cdot \frac{{\partial J\left( n \right)}}{{\partial {w_{ko}}}} = }\\ {\eta \left[ {r\left( t \right) - y\left( t \right)} \right] \cdot \frac{{\partial y\left( t \right)}}{{\partial u\left( t \right)}} \cdot \frac{{\partial u\left( t \right)}}{{\partial {w_{ko}}}} = }\\ {\eta \left[ {r\left( t \right) - y\left( t \right)} \right] \cdot \frac{{\partial y\left( t \right)}}{{\partial u\left( t \right)}} \cdot x_k^{\left( 4 \right)} = }\\ {\eta \left[ {r\left( t \right) - y\left( t \right)} \right] \cdot {\mathop{\rm sgn}} \left[ {\frac{{\partial y\left( t \right)}}{{\partial u\left( t \right)}}} \right] \cdot x_k^{\left( 4 \right)}。} \end{array} $ | (11) |
对象动态特性未知下,∂y(t)/∂u(t)不能精确计算,采用其符号函数sgn[∂y(t)/∂u(t)]近似代替。权值wko迭代更新算法为
| $ \begin{array}{l} {w_{ko}}\left( n \right) = {w_{ko}}\left( {n - 1} \right) + \Delta {w_{ko}}\left( n \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\gamma \left[ {{w_{ko}}\left( {n - 1} \right) - {w_{ko}}\left( {n - 2} \right)} \right]。\end{array} $ | (12) |
同理,隶属函数均值中心mij、标准偏差σij及模糊规则的反馈增益rij的迭代算法依次为
| $ \begin{array}{l} \Delta {m_{ij}}\left( n \right) = - \eta \cdot \frac{{\partial J\left( n \right)}}{{\partial {m_{ij}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\eta \left[ {r\left( t \right) - y\left( t \right)} \right] \cdot {\mathop{\rm sgn}} \left[ {\frac{{\partial y\left( t \right)}}{{\partial u\left( t \right)}}} \right] \cdot net_o^{\left( 4 \right)} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2\left\{ {\left[ {x_i^{\left( 2 \right)} - {m_{ij}} - {r_{ij}} \cdot y_{jp}^{\left( 3 \right)}} \right]} \right\}}}{{{{\left( {{\sigma _{ij}}} \right)}^2}}}, \end{array} $ | (13) |
| $ \begin{array}{l} \Delta {\sigma _{ij}}\left( n \right) = - \eta \cdot \frac{{\partial J\left( n \right)}}{{\partial {\sigma _{ij}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\eta \left[ {r\left( t \right) - y\left( t \right)} \right] \cdot {\mathop{\rm sgn}} \left[ {\frac{{\partial y\left( t \right)}}{{\partial u\left( t \right)}}} \right] \cdot net_o^{\left( 4 \right)} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2{{\left\{ {\left[ {x_i^{\left( 2 \right)} - {m_{ij}} - {r_{ij}} \cdot y_{jp}^{\left( 3 \right)}} \right]} \right\}}^2}}}{{{{\left( {{\sigma _{ij}}} \right)}^3}}}, \end{array} $ | (14) |
| $ \begin{array}{l} \Delta {r_{ij}}\left( n \right) = - \eta \cdot \frac{{\partial J\left( n \right)}}{{\partial {r_{ij}}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\eta \left[ {r\left( t \right) - y\left( t \right)} \right] \cdot {\mathop{\rm sgn}} \left[ {\frac{{\partial y\left( t \right)}}{{\partial u\left( t \right)}}} \right] \cdot net_o^{\left( 4 \right)} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2y_{jp}^{\left( 3 \right)}\left[ {x_i^{\left( 2 \right)} - {m_{ij}} - {r_{ij}} \cdot y_{jp}^{\left( 3 \right)}} \right]}}{{{{\left( {{\sigma _{ij}}} \right)}^2}}}, \end{array} $ | (15) |
| $ \begin{array}{l} {m_{ij}}\left( n \right) = {m_{ij}}\left( {n - 1} \right) + \Delta {m_{ij}}\left( n \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\gamma \left[ {{m_{ij}}\left( {n - 1} \right) - {m_{ij}}\left( {n - 2} \right)} \right], \end{array} $ | (16) |
| $ \begin{array}{l} {\sigma _{ij}}\left( n \right) = {\sigma _{ij}}\left( {n - 1} \right) + \Delta {\sigma _{ij}}\left( n \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\gamma \left[ {{\sigma _{ij}}\left( {n - 1} \right) - {\sigma _{ij}}\left( {n - 2} \right)} \right], \end{array} $ | (17) |
| $ \begin{array}{l} {r_{ij}}\left( n \right) = {r_{ij}}\left( {n - 1} \right) + \Delta {r_{ij}}\left( n \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\gamma \left[ {{r_{ij}}\left( {n - 1} \right) - {r_{ij}}\left( {n - 2} \right)} \right], \end{array} $ | (18) |
式中:γ、η分别为动量因子、学习速率。
4 仿真实验与结果分析 4.1 燃水比控制系统仿真直流锅炉蓄热量小,必须协调燃料、给水动作来响应负荷变化。主汽温控制利用燃水比调节保持中间点温度在设定值,而中间点至过热器出口区段则依靠喷水减温进行调节,以适应过热器的工况变化并维持规定的过热器出口汽温。中间点温度对燃水比扰动响应相对较快,100%负荷下燃水比控制对象[22]为
| $ \begin{array}{l} {G_B}\left( s \right) = \frac{{T\left( s \right)}}{{B\left( s \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{0.03{s^2} + 0.6s + 0.04}}{{{s^3} + 13.6{s^2} + 0.316s + 0.095}}, \end{array} $ | (19) |
| $ \begin{array}{l} {G_W}\left( s \right) = \frac{{T\left( s \right)}}{{W\left( s \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{ - 0.032{s^2} - 1.169s - 0.073}}{{{s^3} + 16.34{s^2} + 5.243s + 0.354}}, \end{array} $ | (20) |
式中:T表示汽水分离器出口汽温;B表示燃料量;W表示给水量。
| 表 1 主汽温对喷水扰动的动态特性 |
由表 1可知,主汽温控制对象迟延、惯性较大,且不同工况下,机组模型结构参数变化较大,若只采集某一工况下的运行数据,其训练所得模型适应能力较差。为此取运行历史记录中,转干态模式至额定工况间的主汽温偏差η(t)、减温水导前汽温偏差z(t)、汽水分离器出口工质温度y(t)及设定值r(t)各200组不同工况对应数据作为训练样本。初始化参数为βth=0.85,σ=0.8,ρ=0.3,τ=0.02,Ith=0.000 1,η=0.25,γ=0.02,rij、mij、σij初值皆取随机数。当中间点温度设定值r(t)与系统响应误差小于允许值时,离线训练完成,控制系统即可投入运行。
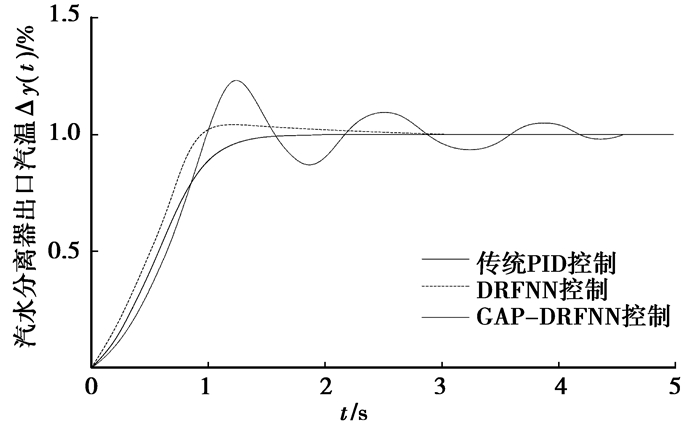
汽水分离器出口汽温阶跃响应实验对比,结果如图 3所示,基于GAP-DRFNN的燃水比控制系统,具有修正网络加权值、中心位置及宽度等参数的能力,且其具备节点生长、修剪能力,使中间点温度输出能较好跟随设定值,上升、调节时间以及超调量等性能均得到显著改善。该方法控制效果明显优于传统PID控制、DRFNN控制,表现出较强的鲁棒性、自适应性及抗模型失配能力。为工况变动下快速、精确控制主蒸汽温度提供有利条件。
|
图 3 燃水比控制阶跃响应曲线 |
在干态运行协调控制模式下,将某厂600 MW火电机组全范围仿真机负荷从450 MW升到600 MW,之后降负荷至450 MW,负荷升降速率取10 MW/min。考查此工况变动过程汽水分离器出口温度与主蒸汽温度变化。
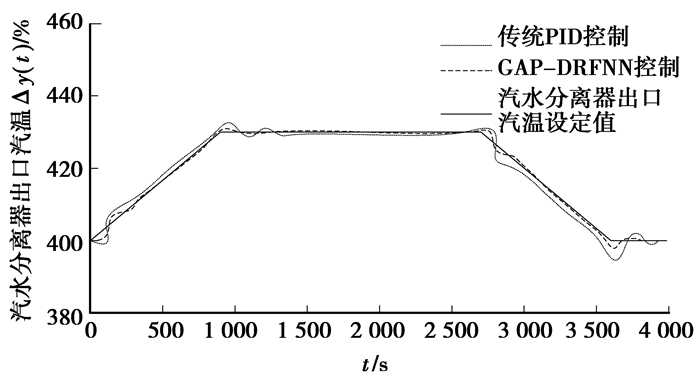
机组变工况,作为锅炉汽温控制导前信号的中间点温度,不仅使气温调节滞后时间大为减小,而且能够及时控制水冷壁工质温度,避免水冷壁出现传热恶化。因此,直接表现燃水比控制效果的中间点温度的控制是锅炉运行关键。如图 4对比可见,在负荷升降开始与结束阶段,常规PID控制因无自整定、自学习能力,中间点温度波动明显,偏差最大值达2.7 ℃和-5.2 ℃,平均2.6 ℃。GAP-DRFNN控制时,只在负荷升降开始与结束阶段中间点温度稍有偏差,中间阶段始终能很好逼近汽温设定值,偏差最大值仅1.8 ℃和-2 ℃,平均0.4 ℃,表明此动态过程控制鲁棒性、自适应性较强。
|
图 4 燃水比变负荷控制试验(汽水分离器出口工质温度) |
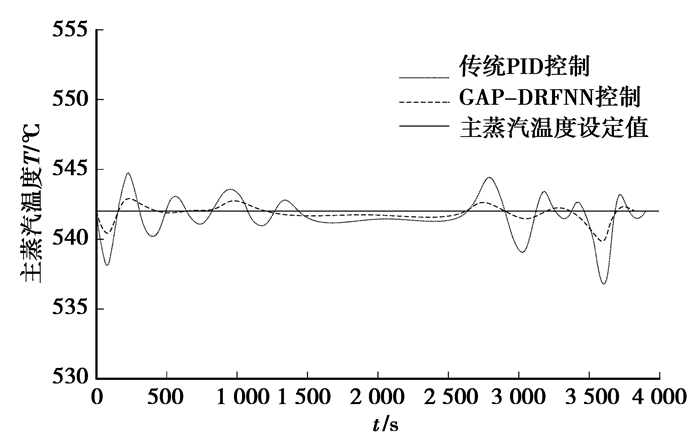
此锅炉在高负荷阶段主蒸汽温度设定值不变,均为542 ℃,工况变动下,具有典型大滞后特性的主蒸汽温度控制尤为困难,这也对粗调节主蒸汽温度的燃水比控制提出更高要求。如图 5所示,常规PID控制,锅炉工况波动较大,主蒸汽温度偏差最大2.8 ℃和-5.1 ℃,均值为2.4 ℃。燃水比在GAP-DRFNN控制下,中间点温度已得到较好控制,从而为主蒸汽温度精确调整提供保证。主蒸汽温度偏差只在负荷变动初始与结束时稍微扰动。其最大值仅为1 ℃和-2.1 ℃,主汽温平均偏差为0.55 ℃,体现了GAP-DRFNN较好地非线性适应能力及动态过程控制能力。
|
图 5 燃水比变负荷控制试验(主蒸汽温度) |
生长-剪枝动态递归模糊神经网络燃水比控制系统,融合了模糊控制的良好鲁棒性、自适应性特点与神经网络的逼近非线性、强自学习能力,且其反馈单元能够记忆过去时刻神经网络的输出,使系统具有动态特性,燃水比控制超调量小,稳态误差小且能够迅速响应。在煤质变化、负荷变动等扰动下,神经网络通过结构学习,自动增加和修剪神经元,而且根据梯度下降法,动态调整网络的隶属函数参数以及神经网络递归权值,有利于GAP-DRFNN适应燃水比变工况控制时的需要。利用热量信号优化燃水比控制,燃水比信号更加精确,但寻求更快速、准确的燃水比调节校正信号对于提高燃水比的调节速度和精度具有重要意义。
| [1] |
樊泉桂.
1000 MW超超临界锅炉中间点温度和汽温控制[J]. 动力工程, 2007, 27(3): 332–335.
FAN Quangui. Temperature at intermediate points of 1000MW ultra-supercritical boilers and their steam temperature control[J]. Journal of Power Engineering, 2007, 27(3): 332–335. (in Chinese) |
| [2] |
于达仁, 范轶, 徐志强.
基于分布信息融合的直流锅炉燃料量信号重构[J]. 中国电机工程学报, 2004, 24(2): 191–195.
YU Daren, FAN Yi, XU Zhiqiang. Reconstruction for fuel signal of once-through boiler based on distributed data fusion[J]. Proceedings of the CSEE, 2004, 24(2): 191–195. (in Chinese) |
| [3] |
李阳春, 卫成业, 罗志浩, 等.
以炉膛辐射信号为中间被调量的串级模糊调节策略研究[J]. 中国电机工程学报, 2001, 21(6): 80–83.
LI Yangchun, WEI Chengye, LUO Zhihao, et al. Cascade fuzzy control system based on the radiation signal of the furnace[J]. Proceedings of the CSEE, 2001, 21(6): 80–83. (in Chinese) |
| [4] |
韩忠旭, 周传心, 李丹, 等.
燃煤发热量软测量技术及其在超临界机组控制系统中的应用[J]. 中国电机工程学报, 2008, 28(35): 90–95.
HAN Zhongxu, ZHOU Chuanxin, LI Dan, et al. Soft measurement technology of coal-fired heat and its application on supercritical generating unit control system[J]. Proceedings of the CSEE, 2008, 28(35): 90–95. DOI:10.3321/j.issn:0258-8013.2008.35.015 (in Chinese) |
| [5] | Paranjape R D.Modeling and control of a supercritical coal fired boiler[D].Texas:Texas Tech University, 1996. https://www.coursehero.com/file/24142211/UG-courses-of-study-2007pdf/ |
| [6] |
夏明.
超临界机组汽温控制系统设计[J]. 中国电力, 2006, 39(3): 74–77.
XIA Ming. The design of steam temperature control systems for supercritical generation units[J]. Electric Power, 2006, 39(3): 74–77. (in Chinese) |
| [7] |
刘潇, 曹冬林, 丁劲松.
外高桥1000 MW超超临界机组闭环控制系统设计[J]. 中国电力, 2006, 39(3): 70–73.
LIU Xiao, CAO Donglin, DING Jinsong. Closed loop control system design for Waigaoqiao 1000MW ultra-supercritical power unit[J]. Electric Power, 2006, 39(3): 70–73. (in Chinese) |
| [8] | Zhu H L, Liu J Z, Chang T H, et al. Internal model control using LMS filter and its application to superheated steam temperature of power plant[C]//Proceedings of the 20102nd International Conference on Computer and Automation Engineering, February 26-28, 2010, Singapore. Piscataway:IEEE Press, 2010, 2:135-138. |
| [9] |
王东风, 韩璞, 郭启刚.
锅炉过热汽温系统的DRNN网络自整定PID控制[J]. 中国电机工程学报, 2004, 24(8): 196–200.
WANG Dongfeng, HAN Pu, GUO Qigang. A diagonal recurrent neural network self-tuning PID control for superheated steam temperature system[J]. Proceedings of the CSEE, 2004, 24(8): 196–200. (in Chinese) |
| [10] |
王耀南, 王辉, 邱四海, 等.
基于递归模糊神经网络的感应电机无速度传感器矢量控制[J]. 中国电机工程学报, 2004, 24(5): 84–89.
WANG Yaonan, WANG Hui, QIU Sihai, et al. The field-oriented control for speed-sensorless induction motor drive based on recurrent fuzzy neural network[J]. Proceedings of the CSEE, 2004, 24(5): 84–89. (in Chinese) |
| [11] |
彭金柱, 王耀南, 王杰.
基于递归模糊神经网络的机器人鲁棒H∞跟踪控制[J]. 控制理论与应用, 2010, 27(9): 1145–1151.
PENG Jinzhu, WANG Yaonan, WANG Jie. Robust H-infinity tracking-control for robotic system based on recurrent fuzzy-neural-networks[J]. Control Theory & Applications, 2010, 27(9): 1145–1151. (in Chinese) |
| [12] |
张桂臣, 马捷.
滑模动态递归模糊神经网络船电推进复合控制[J]. 控制理论与应用, 2011, 28(5): 625–630.
ZHANG Guichen, MA Jie. Hybrid control based on sliding mode-dynamic recursive fuzzy neural network for marine electrical propulsion[J]. Control Theory & Applications, 2011, 28(5): 625–630. (in Chinese) |
| [13] | Lin C J, Chen C H. Identification and prediction using recurrent compensatory neuro-fuzzy systems[J]. Fuzzy Sets and Systems, 2005, 150(2): 307–330. DOI:10.1016/j.fss.2004.07.001 |
| [14] | Zhang L J, Qi X, Pang Y J. Adaptive output feedback control based on DRFNN for AUV[J]. Ocean Engineering, 2009, 39(9/10): 716–722. |
| [15] | Zhang Q Z, Gan W S, Zhou Y L. Adaptive recurrent fuzzy neural networks for active noise control[J]. Journal of Sound and Vibration, 2006, 296(4/5): 935–948. |
| [16] | Hsu C F, Cheng K H. Recurrent fuzzy-neural approach for nonlinear control using dynamic structure learning scheme[J]. Neurocomputing, 2008, 71(16/17/18): 3447–3459. |
| [17] | Huang G B, Saratchandran P, Sundararajan N. A generalized growing and pruning RBF (GGAP-RBF)neural network for function approximation[J]. IEEE Transactions on Neural Networks, 2005, 16(1): 57–67. DOI:10.1109/TNN.2004.836241 |
| [18] | Li S Y, Chen Q, Huang G B. Dynamic temperature modeling of continuous annealing furnace using GGAP-RBF neural network[J]. Neurocomputing, 2006, 69(4/5/6): 523–536. |
| [19] | Bortman M, Aladjem M. A growing and pruning method for radial basis function networks[J]. IEEE Transactions on Neural Networks, 2009, 20(6): 1039–1045. DOI:10.1109/TNN.2009.2019270 |
| [20] | Zhang R X, Huang G B, Sundararajan N, et al. Improved GAP-RBF network for classification problems[J]. Neurocomputing, 2007, 70(16/17/18): 3011–3018. |
| [21] | Chen L, Xie Y C, Shen Z L, et al.Modeling of the combustion optimizing based on RBF neural networks[C]//Proceedings of the 2008 ISECS International Colloquium on Computing, Communication, Control, and Management, August 3-4, 2008, Guangzhou, China. Piscataway:IEEE Press, 2008, 2:95-98. |
| [22] | 李凤翎. 超临界机组中间点温度控制的研究与仿真[D]. 石家庄: 华北电力大学, 2009. http://www.cnki.com.cn/Article/CJFDTOTAL-ZSJS201105013.htm |
 2013, Vol. 36
2013, Vol. 36

