2. 重庆大学 机械工程学院, 重庆 400044
2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China
全地形车是一种全新概念的新车型,适合在各种地形下行驶。全地形车车架是整车的关键部件,在整车操纵稳定性、行驶安全性、乘坐舒适性和可靠性等方面起着十分重要的作用。由于行驶的路况通常比较恶劣,车架在行驶的过程中受力情况复杂,不仅要求车架有足够的强度和刚度,而且要求其质量越轻越好。在产品设计阶段,对全地形车车架的轻量化研究不仅对减少原材料的浪费、降低生产成本和提高产品竞争力都具有很重要的实际意义,而且对新产品的开发具有重要的指导作用。
车架轻量化一般有2种途径:一是应用新材料减轻车架结构质量[1-2];二是在保证承载能力和可靠性的前提下根据经验适当减轻质量[3-4]。前者轻量化效果比较明显,但新材料的成本高和工艺复杂;后者轻量化的途径容易实现,并且轻量化效果良好,但轻量化过程中存在盲目性,很容易造成车架结构强度分配不合理。随着现代设计方法不断提高,运用有限元分析方法实现轻量化设计使设计过程可预见、可控制。Mayer[5],Sobieski[6]利用计算机技术分别考虑了车架在碰撞、振动过程中的各种约束,将安全性和舒适性引入轻量化设计过程中,这为全地形车的轻量化研究提供了技术上的借签。目前对全地形车结构轻量化的研究尚不多。朱茂桃等[7]只是根据经验减小车架厚度尺寸而达到轻量化的目的,许佩霞等[8]根据经验选择优化过程中的设计变量来实现结构优化。考虑到全地形车车架包含的零部件比较多,如果把所有部件都选为设计变量会增加设计时间和成本,因此利用灵敏度分析结果选择设计变量可以提高优化设计效率。
在建立全地形车车架有限元模型的基础上,对车架结构进行模态分析,对比实验结果验证了所建立模型的有效性,进一步分析其静态应力变形情况和车架结构灵敏度,并提出了轻量化方案,经过验证取得了较好的减重效果。
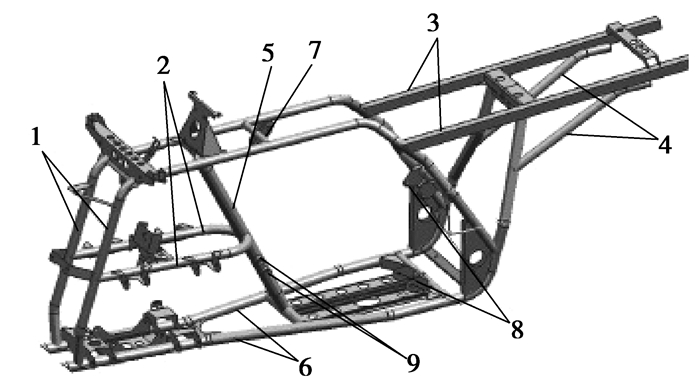
1 全地形车车架有限元模态分析 1.1 全地形车车架有限元模型的建立根据某型全地形车车架的二维图纸,利用三维建模软件CATIA建立该车架的三维几何模型,考虑到一些小部件对车架总质量影响不大,故对其进行了一些简化,最终建立模型如图 1所示。车架材料采用10和Q345,其中除车架左右上管采用Q345外其余都采用10,其材料的力学性能如表 1所示。
|
图 1 全地形车车架三维模型 1.车架左右上管;2.左右联接管;3.方管组合;4.左右后支承管;5.前撑管;6.车架左右下管;7.发动机前上支承;8.发动机后支承;9.发动机衬管 |
| 表 1 车架材料的力学性能 |
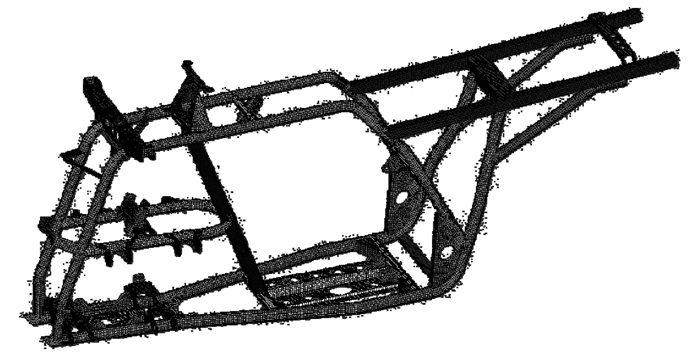
分析该全地形车车架发现,车架主要是由各种截面的薄壁管焊接而成,其厚度与长度和截面尺寸相比很小,因此采用shell63单元能够很好地表达其结构特性[9-10]。采用HyperMesh对车架进行有限元网格划分,划分过程中忽略焊点对结构刚度的影响,直接采用壳单元连接[11]。最终建立的有限元模型如图 2所示。
|
图 2 全地形车车架有限元模型 |
利用optistruct求解器对全地形车车架进行自由状态下的模态分析,设定频率范围为0~200 Hz,提取前6阶的自由模态值。
实验模态分析即是通过对系统施加某种激励,测出相应的响应,根据频响函数来识别结构的模态参数[12],试验模态分析可以用来验证有限元模型及计算模态分析的准确性。
为模拟车架的自由状态,实验时将车架用软橡皮绳悬挂起来,采用力锤激励。实验后测得的实验模态与计算模态值比较如表 2所示。
| 表 2 车架计算模态和实验模态对比 |
由表 2可以看出,计算模态和实验模态相对误差值都比较小,说明以上建立的有限元模型比较准确,可以依此模型来进行轻量化分析。
2 全地形车车架工况应力变形分析 2.1 载荷条件全地形车整车的基本载荷主要由车架承担,所有载荷以均布载荷或者集中载荷的方式加到相应的节点和单元上,其中主要包括车架自身的重量、乘员的重量、发动机及底盘的重量、满载时货物的重量以及油箱和油的重量等。在施加载荷的过程中将油箱的质量取油箱的容积与汽油密度的乘积,并以集中载荷的形式加载到油箱与车架连接处,发动机的质量以集中载荷的形式加载到发动机质心,货物与乘员质量以均布载荷的方式加载到后货架梁上[13],具体数值见表 3。
| 表 3 车架所承受的主要载荷 |
由于全地形车行驶路况复杂,针对实际情况中的水平弯曲,极限扭转(左后轮悬空)、紧急制动和紧急转弯4种工况进行仿真分析。4种工况下的边界条件如下[14]
1) 水平弯曲,在满载情况下对4个车轮的中心进行全约束,即约束6个自由度。
2) 极限扭转(左后轮悬空),在满载情况下约束右后轮中心的3个平动自由度,释放3个转动自由度,释放左后轮中心的所有自由度并且在其中心加上后轮胎的重量270 N;约束前轮中心的垂直自由度,释放其他自由度。
3) 紧急制动,在满载情况下考虑前后轮抱死的情况,以最大的制动加速度0.8 g制动,在载荷相应的位置施加惯性制动力。约束前轮中心的3个平动自由度,释放3个转动自由度;约束后轮中心的垂直和纵向自由度,释放其他自由度。
4) 紧急转弯,在满载情况下考虑除水平弯曲工况下的载荷外,还施加0.4 g的离心加速度均布在相应的位置。约束前、后轮中心的3个平动自由度,释放3个转动自由度。
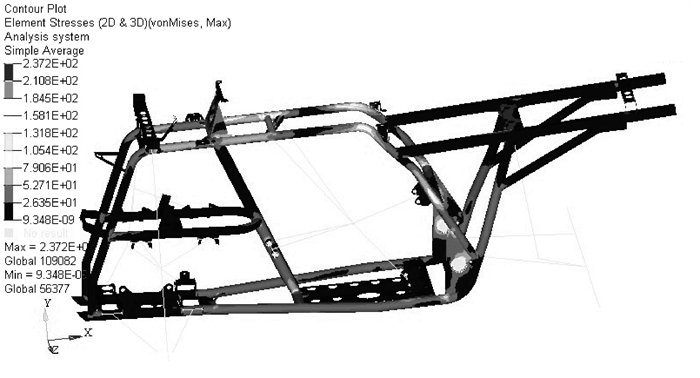
2.3 分析结果分别将4种工况的有限元模型提交到Optistruct求解器中进行分析,得到全地形车车架在4种工况下应力和变形结果,其中极限扭转工况下的应力和变形云图如图 3、图 4所示。
|
图 3 极限扭转工况的应力云图 |
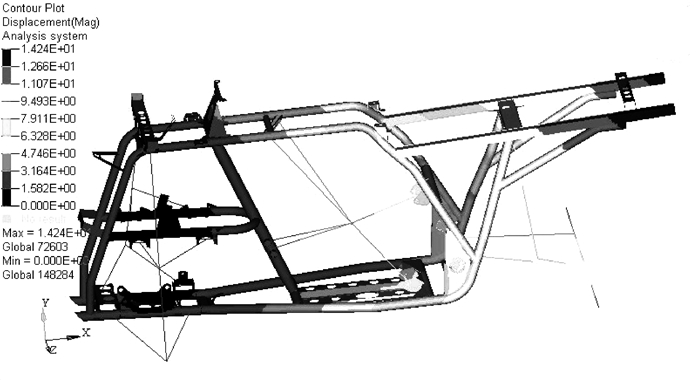
|
图 4 极限扭转工况的变形云图 |
极限扭转工况下车架的受力和变形最为严重,最大应力为237 MPa,发生在右上主管靠近与发动机上支承联接管处,最大位移14.24 mm发生在车架左货架尾部,其余工况下最大应力分别为55.58 MPa,69.95 MPa和69.43 MPa,最大变形分别为1.13 mm,1.65 mm和1.583 mm。车架材料为Q345钢,其屈服极限值为345 Mpa,此时车架的安全系数为1.46,车架满足强度要求,同时有一定的富余量,可以进一步进行结构的轻量化设计。
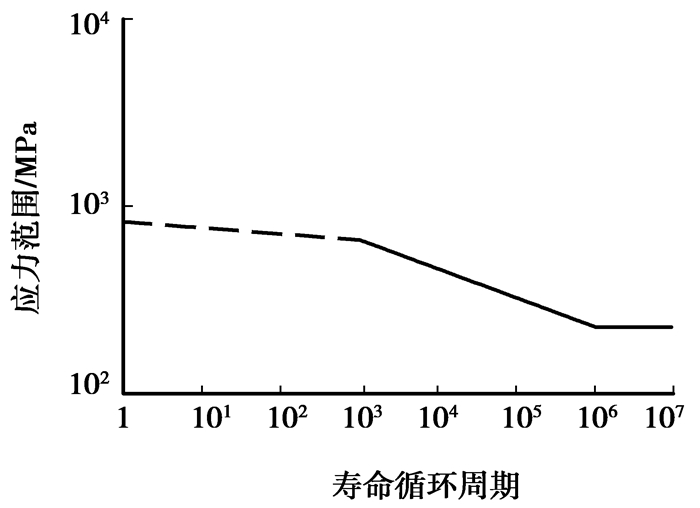
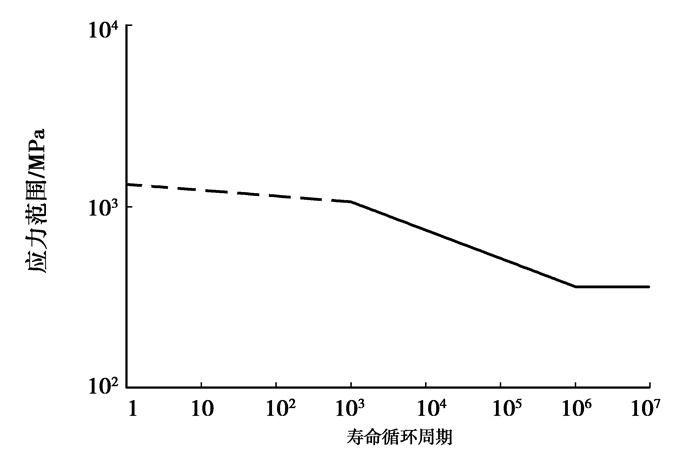
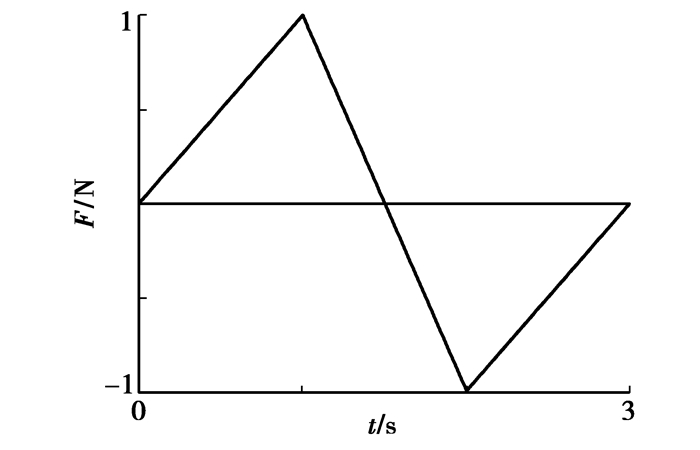
3 全地形车车架疲劳寿命分析对车架进行疲劳寿命分析必需具备三大条件,即结构的几何特征、材料的疲劳属性及载荷时间历程。前面分析得到的有限元模型及应力结果即是结构的几何特征。根据车架的材料10和Q345,取可靠度为99%的疲劳寿命曲线,在MSC.fatigue中得到材料S-N曲线[15]如图 5、图 6所示;本文研究的对象属于高周疲劳,其总体应力水平不高,应变相对较小,适合选用名义应力法来计算疲劳寿命。车架系统中的载荷是外部集中载荷,以时间历程的形式来定义,故采用图 7所示的载荷时间曲线。
|
图 5 10的S-N曲线 |
|
图 6 Q345的S-N曲线 |
|
图 7 载荷时间曲线 |
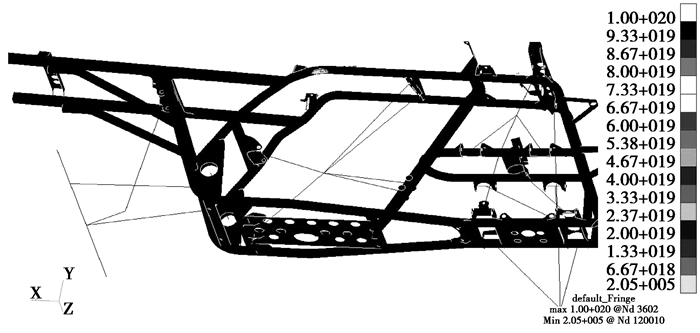
将上面得到的车架结构应力值、材料的疲劳属性及载荷时间曲线输入到MSC.fatigue软件中,进行车架结构疲劳分析,得到车架结构在4种工况下的疲劳寿命结果,其中极限扭转工况下疲劳寿命云图如图 8所示。
|
图 8 极限扭转工况疲劳寿命云图 |
根据分析结果,除了极限扭转工况下最低疲劳寿命为205 000个周期外,其余工况下的疲劳寿命均为无限寿命,其中最低寿命发生在车架右上管后弯折处。
4 车架结构灵敏度分析及轻量化设计 4.1 灵敏度分析的理论基础灵敏度是关注指标对某些结构参数xj的变化梯度。从数学意义上讲,灵敏度为:若一函数ui可导,其一阶灵敏度[16]在连续系统中可表示为
| $ {\rm{Sen(}}\frac{{{u_i}}}{{{x_j}}}{\rm{)}} = \frac{{\partial {u_i}}}{{\partial {x_j}}}, $ | (1) |
式中:ui为车架结构性能参数;xj为车架结构设计参数。
现代的设计分析软件引入了灵敏度分析的功能模块,使灵敏度的计算分析成为方便有效的结构分析方法。而设计分析软件中的灵敏度分析大多是利用设计优化模块提供的优化方法中的梯度评估工具进行的,因此可以计算目标函数和状态变量对设计变量在某一参考点的梯度,即灵敏度为
| $ {\rm{Sen(}}\frac{{{u_i}}}{{{x_j}}}{\rm{) = }}\frac{{\partial {u_i}}}{{\partial {x_j}}} = \frac{{{u_i}(\mathit{X + }\Delta {x_i}\mathit{\boldsymbol{e}}) - {\mathit{u}_i}(\mathit{x})}}{{\Delta {x_j}}}, $ | (2) |
式中:X为由参考点处所有的车架结构设计参数组成的向量;Δxj为车架结构设计参数的变化,缺省值为xi上、下限之差的1%;e为X同维数的向量。
4.2 车架灵敏度分析及轻量化设计优化设计中需要定义优化3要素:目标函数、约束条件和设计变量,具体的数学模型表达式[17]为
| $ \left\{ \begin{array}{l} {{\bar v}_{\min }} \le \mathit{\boldsymbol{\bar v}} \le {{\bar v}_{\max }}。\;\;\;\mathit{\boldsymbol{\bar v}} = [{\mathit{v}_1}, {\mathit{v}_2}, \cdot \cdot \cdot, {\mathit{v}_n}], \\ {{\bar w}_{\min }} \le \mathit{\boldsymbol{\bar w}} \le {{\bar w}_{\max }}, \;\mathit{\boldsymbol{\bar w}} = [{\mathit{w}_1}, {\mathit{w}_2}, \cdot \cdot \cdot, {\mathit{w}_{\rm{m}}}], \\ \min f(\mathit{\bar v})。\end{array} \right. $ |
式中:v为设计变量;w为约束条件;f(v)为目标函数。
目标函数是在满足应力和位移的要求下达到质量最小。由于质量与体积呈线性变化(密度均匀时),体积最小意味着质量最小。因此把目标函数定义为结构的体积最小。
约束条件是指约束设计的数值,一般是设计变量的函数。轻量化通过截面形状尺寸数值的改变来实现,同时要保证车架的强度与刚度的要求。因此,将车架的应力和位移定义为约束条件,实现“等强度,等刚度”的要求[18]。
在优化过程中,根据灵敏度分析结果确定优化变量[19]。即先对参数进行灵敏度分析,选取车架结构中主要的零件进行灵敏度分析。分别计算出目标函数和约束条件对每个设计变量的灵敏度值,从高刚度轻质量的角度考虑,对刚度与质量进行权衡,利用求得的灵敏度值计算Sv/Sd,灵敏度分析结果如表 4所示。
| 表 4 车架灵敏度分析 |
根据Sv/Sd的结果,选取T1,T6,T8,T10,T11,T12,T14,T15,T16,T17,T18,T20,T22,T23,T24,T25作为设计变量。
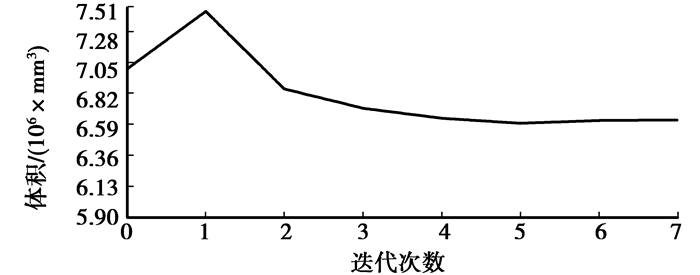
4.3 轻量化结果根据前面确定的车架优化的设计变量、目标函数和约束条件后,提交给Optistruct求解器分析,经过7步迭代后得到车架尺寸优化的结果如表 5所示,优化过程中目标函数的变化曲线图如图 9所示。最终减重了6.606 3 kg,优化后车架总体质量减轻了25.9%。
| 表 5 车架尺寸优化结果 |
|
图 9 目标函数变化曲线图 |
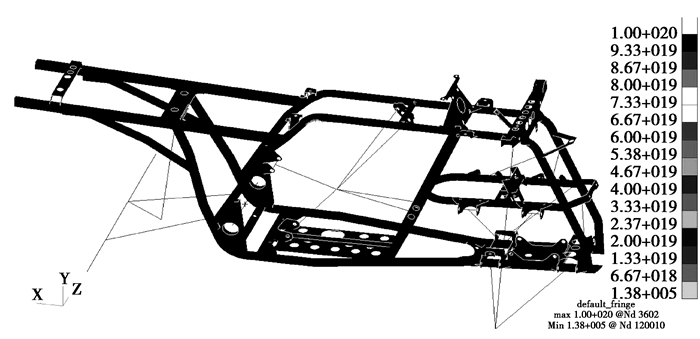
为了验证以上优化结果是否有效以及车架能否达到预期的疲劳寿命,按优化后的参数修改车架然后进行有限元强度刚度校核及疲劳分析,优化前后的最大应力值及变形量对比如表 6所示。极限扭转工况疲劳寿命结果如图 10所示。
| 表 6 优化前后最大应力值对比 |
|
图 10 极限扭转工况疲劳寿命云图 |
根据对比发现,优化后4种工况下车架的强度和刚度都有所下降,但最大应力值均小于材料的屈服极限,同时应力分布情况同优化前相同,变形量也在允许范围之内,优化后车架的安全系数为1.36,可见优化后车架强度满足其设计要求。
根据优化后车架各种工况疲劳分析结果可知,除极限扭转工况的最低寿命为138 000个周期外,其余工况的疲劳寿命均为无限寿命,最低寿命也发生在右上管后弯折处。通过优化后疲劳寿命分析可知,沙滩车在实际使用过程中要尽量避免一轮悬空的情况,优化后车架的疲劳寿命基本上能够满足设计要求(13×104次)。
5 结论通过对全地形车车架结构进行有限元静力学分析和疲劳分析,在进一步分析车架结构灵敏度的基础上,对车架结构进行参数化优化设计,优化效果比较明显。根据优化后车架强度分析和疲劳寿命结果验证了优化的有效性,优化后车架质量减轻了25.9%。同时表明,灵敏度分析是确定优化设计过程中设计变量的有效方法。
| [1] |
李桂华, 熊飞, 龙江启.
车身材料轻量化及其新技术的应用[J]. 材料开发与应用, 2009, 24(2): 87–93.
LI Guihua, XIONG Fei, LONG Jiangqi. Applications of lightweight of car body material and new technology[J]. Development and Application of Material, 2009, 24(2): 87–93. (in Chinese) |
| [2] |
冯美斌.
汽车轻量化技术中新材料的发展及应用[J]. 汽车工程, 2006, 28(3): 213–220.
FENG Meibin. Development and applications of new materials in automotive lightweighting technologies[J]. Automotive Engineering, 2006, 28(3): 213–220. (in Chinese) |
| [3] |
程耿东, 顾元宪, 王健.
我国机械优化研究与应用的综述和展望[J]. 机械强度, 1995, 17(2): 68–74.
CHEN Gengdong, GU Yuanxian, WANG Jian. Aprospective review on research and application of optimal design of mechanical systems in China[J]. Journal of Mechanical Strength, 1995, 17(2): 68–74. (in Chinese) |
| [4] | Fukushina J, Suzuki K, Kikuchi N. Shape and topology optimization of a car body with multiple loading condition[C]//Proceedings of the International Congress & Exposition, February 24, 1992, Detroit, Michigan, United States.[S.l.]:SAE Technical Papers, 1992:920777. https://ar.scribd.com/document/315330230/Topology-Optimization |
| [5] | Mayer R R, Kikuchi N, Scott R A. Application of topological optimization techniques to structural crashworthiness[J]. International Journal for Numerical Methods in Engineering, 1996, 39(8): 1383–1403. DOI:10.1002/(ISSN)1097-0207 |
| [6] | Sobieszczanski-Sobieski J, Kodiyalam S, Yang R Y. Optimization of car body under constraints of noise, vibration, and harshness (NVH), and crash[J]. Structural and Multidisciplinary Optimization, 2001, 22(4): 295–306. DOI:10.1007/s00158-001-0150-6 |
| [7] |
朱茂桃, 蔡炳芳, 束荣军, 等.
全地形车车架结构有限元分析与轻量化设计[J]. 拖拉机与农用运输车, 2008, 35(3): 47–48, 52.
ZHU Maotao, CAI Binfang, SU Rongjun. FEA and lightweight design for ATV frame structure[J]. Tractor and Farm Transporter, 2008, 35(3): 47–48, 52. (in Chinese) |
| [8] |
许佩霞, 蔡炳芳.
基于ANSYS的全地形车车架结构优化设计[J]. 机械设计, 2008, 25(12): 56–58.
XU Peixia, CAI Binfang. Structural optimization design on frame of all topography vehicle based on ANSYS[J]. Journal of Machine Design, 2008, 25(12): 56–58. (in Chinese) |
| [9] |
朱茂桃, 蔡炳芳, 束荣军, 等.
全地形车车架的动态性能分析与减振研究[J]. 中国机械工程, 2008, 19(12): 1508–1511.
ZHU Maotao, CAI Binfang, SU Rongjun, et al. Analysis on dynamic performance of ATV frame and its vibration reduction[J]. China Mechanical Engineering, 2008, 19(12): 1508–1511. DOI:10.3321/j.issn:1004-132X.2008.12.027 (in Chinese) |
| [10] | Ibrahim I M, Crolla D A, Barton D C. Effect of frame flexibility on the ride vibration of trucks[J]. Computer and Structures, 2004, 58(4): 709–713. |
| [11] |
徐中明, 郭师峰, 张志飞, 等.
全地形车车体动态特性分析[J]. 重庆大学学报, 2009, 32(1): 6–10.
XU Zhongming, GUO Shifeng, ZHANG Zhifei, et al. Dynamic characteristic analysis of an all-terrain vehicle body[J]. Journal of Chongqing University, 2009, 32(1): 6–10. DOI:10.11835/j.issn.1000-582X.2009.01.002 (in Chinese) |
| [12] | Peeters B, Antonnio V, Herman V D A. PolyMAX modal parameter estimation from operational data[M]. Leuven: Katholieke University, 2004. |
| [13] |
邹喜红, 毛星子, 税宁, 等.
LX200摩托车车架有限元分析及强度评价[J]. 重庆工学院学报:自然科学版, 2009, 23(5): 7–10.
ZOU Xihong, MAO Xingzi, SHUI Ning, et al. Finite element analysis and strength appraisement of LX200 motorcycle frame[J]. Journal of Chongqing Institute of Technology:Natural Science, 2009, 23(5): 7–10. (in Chinese) |
| [14] |
赵韩, 姜康, 曹文钢, 等.
半承载式客车车身结构有限元分析[J]. 汽车工程, 2007, 29(4): 346–351.
ZHAO Han, JIANG Kang, CAO Wengang, et al. Finite element analysis for half-integral body structure of buses[J]. Automotive Engineering, 2007, 29(4): 346–351. (in Chinese) |
| [15] | 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2003. |
| [16] | Nalecz A G. Application of sensitivity method to snalysis and dynthesis of vehicle dynamic system[J]. Vehicle System Dynamics, 1989(1/2/3): 1–44. |
| [17] | 刘惟信. 机械最优化设计[M]. 2版. 北京: 清华大学出版社, 1994. |
| [18] |
曹文钢, 曲令晋, 白迎春.
基于灵敏度分析的客车车身质量优化研究[J]. 汽车工程, 2009, 31(3): 278–281.
CAO Wengang, QU Lingjin, BAI Yingchun. A study on the mass optimization of bus body based on sensitivity analysis[J]. Automotive Engineering, 2009, 31(3): 278–281. (in Chinese) |
| [19] |
瞿晓彬, 何志刚, 张敏中, 等.
城市客车车身结构灵敏度分析及优化[J]. 机械设计与制造, 2007(1): 79–80.
QU Xiaobin, HE Zhigang, ZHANG Mingzhong, et al. Sensitivity analysis and optimization of city bus body[J]. Mechanical Design and Manufacture, 2007(1): 79–80. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


