随着CMOS技术不断地发展,CMOS电子器件也被运用到各个领域。但是在诸如太空探测、粒子物理实验以及医学成像等电离辐射环境中使用的CMOS器件,会受到辐射引起的辐射总剂量效应(radiation total dose effect, RTDE)[1]和单粒子翻转效应(single event upset, SEU)[2-3]等的影响,可能导致工作异常甚至损坏。为了提高电子器件在辐射环境中工作的稳定性和工作时间,研究者从器件级和电路级都提出了许多方法[4-6]。目前在抗RTDE效应方面,从MOS器件结构上提高晶体管耐辐射能力的方法主要是避免NMOS管的源漏端与厚的场氧相连,主要有环状栅(annular or endless gate)的MOS晶体管版图结构[7]和Dog Bone栅MOS晶体管的版图结构[8]。环状栅结构虽然避免了源漏之间场氧的出现,然而存在源漏端不对称、受最小宽长比约束等缺点。Dog Bone栅MOS场效应晶体管的版图结构是在常规版图结构基础上用多晶硅覆盖源漏区边缘而形成(如图 1所示),即在源漏边缘处用薄的栅氧取代了厚的场氧。因此,Dog Bone栅MOS场效应晶体管源漏端对称且设计灵活。但是对于这类进行了辐射加固设计的特殊版图结构,由于其电流电压特性与同尺寸的普通结构晶体管的有所不同,给集成电路设计带来了一定问题。文中采用Silvaco工艺与器件仿真软件,对标准CMOS工艺下的Dog Bone结构的辐射加固MOS器件进行了建模仿真,将之与普通结构MOS器件相比较,以寻求一种Dog Bone栅MOS场效应晶体管等效宽长比的计算方法,为进一步的电路设计打下基础。
|
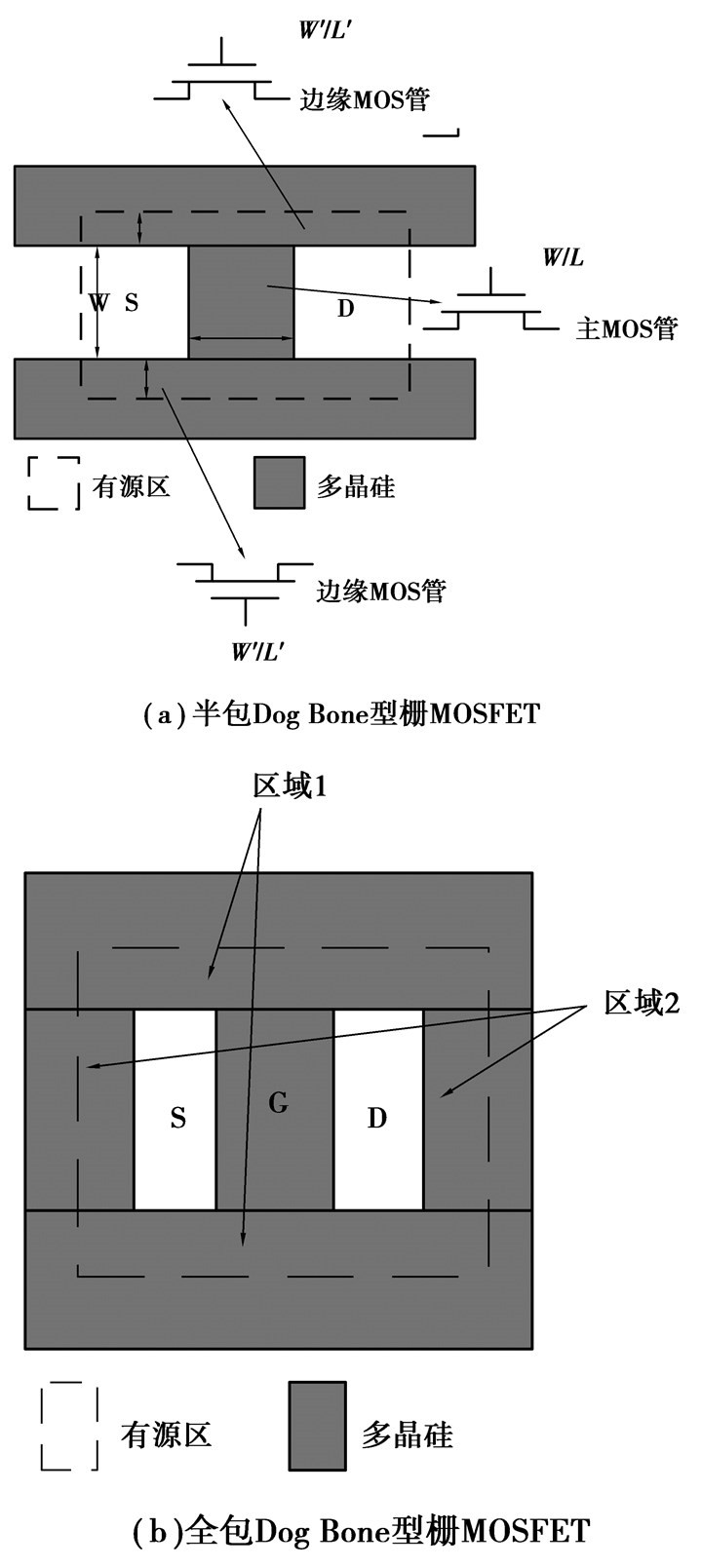
图 1 Dog Bone栅MOS FET的版图结构 |
利用Silvaco TCAD平台,使用工艺仿真器(ATHENA)、三维器件编辑器(DEVEDIT3D)和器件仿真器(ATLAS)。实验样管拟采用CSMC 0.5 μm CMOS工艺流片,为了与厂家提供的参数吻合,首先使用ATHENA工艺仿真提取出具体的工艺参数(如衬底掺杂、源漏扩散、阈值调节注入等),使所得器件的阈值电压和各部分方块电阻与厂家基本吻合。再根据工艺仿真提取的参数和厂家提供的部分参数,用三维器件编辑器DEVEDIT3D生成器件结构。最后用器件仿真器ATLAS对生成的结构进行仿真。
在ATLAS的器件仿真过程中,物理模型采用Boltzmann载流子统计模型,SRH (Shockley-Read-Hall)复合模型,CVT载流子迁移率模型;数值仿真采用Newton-Richardson迭代算法[8]。
在Dog Bone栅MOS场效应晶体管的2种结构(见图 1)中,图 1(b)源漏两端完全被多晶硅包围,可以防止该晶体管和相邻管子之间的连通。利用ATLAS对这2种结构进行电学仿真,结果表明,在相同的偏置下这2种结构在周围无其他器件存在时有相同的输出电流,且在栅极正向偏置下,图 1(b)的区域2没有贡献额外的电流密度(如图 2所示,为便于观察,图中MOS管未显示多晶硅层和氧化层),因此以下的仿真分析只对图 1(a)结构进行。
|
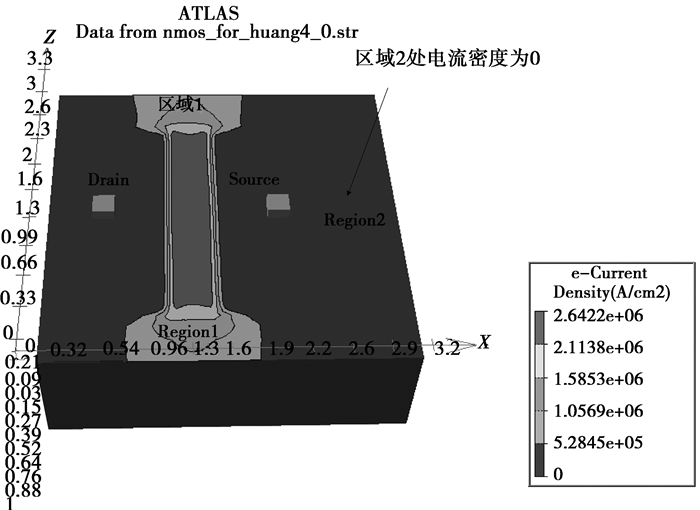
图 2 源漏全包的Dog Bone栅MOS结构表面电流密度分布 |
将Dog Bone栅MOS管结构划分为普通结构的MOS管(主MOS管)和等效的边缘MOS管2部分的并联,见图 1(a),则整个Dog Bone栅MOS管的等效宽长比按照式(1) 计算。
| $ {\left( {\frac{W}{L}} \right)_{{\rm{eq}}}} = {\rm{finger}} \times {\left( {\left( {\frac{W}{L}} \right.} \right)_{{\rm{host}}}} + 2 \times \left( {{{\left. {\frac{{W'}}{{L'}}} \right)}_{{\rm{edge}}}}} \right), $ | (1) |
式中:
| $ {g_m} = \mu {C_{{\rm{ox}}}}{\left( {\frac{W}{L}} \right)_{{\rm{eq}}}}({{V}_{{\rm{GS}}}} - {{V}_{{\rm{TH}}}}), $ | (2) |
式中:μ为电子迁移率;Cox为单位面积栅氧化层电容;
利用ATLAS分别仿真了主MOS管的沟道长度、宽度及边缘MOS管中多晶硅和有源区的重叠宽度d的大小对边缘MOS管等效宽长比大小的影响。
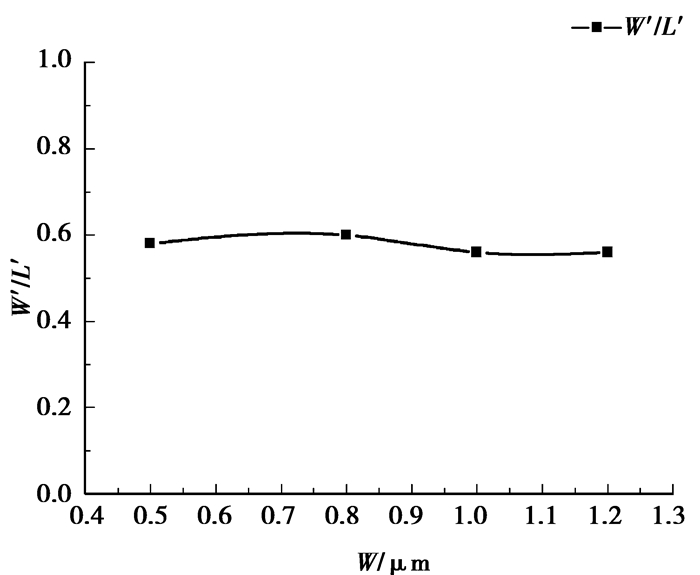
1) 主MOS的沟道宽度对边缘MOS等效宽长比的影响。用ATLAS对边缘MOS的多晶硅和有源区的重叠宽度d=0.5 μm,主MOS的长度L=0.5 μm,宽度W分别为0.5,0.8,1,1.2 μm的4种Dog Bone MOS管结构进行仿真,由其电压-电流曲线计算等效宽长比。得到边缘MOS等效宽长比随主MOS沟道宽度W变化的曲线,如图 3所示。由图可见,边缘MOS等效宽长比几乎不受主MOS沟道的宽度的影响。因为主MOS的沟道宽度变化前后不会对边缘MOS的沟道横向电场产生影响。
|
图 3 边缘MOS等效宽长比和主MOS的宽度之间的关系 |
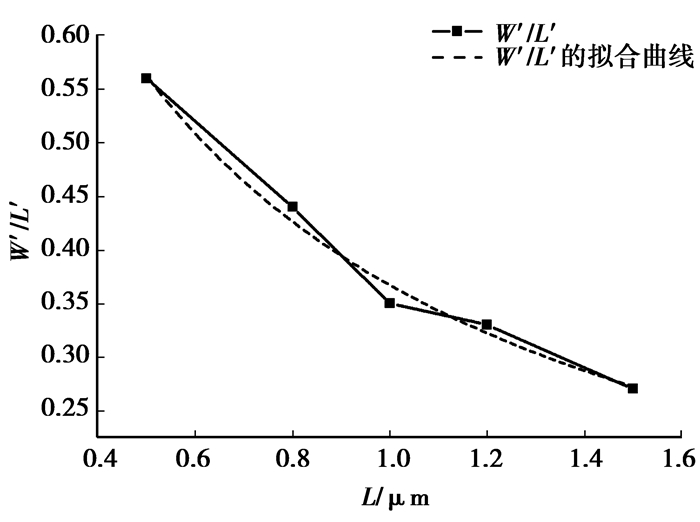
2) 主MOS的沟道长度L对边缘MOS等效宽长比的影响。用ATLAS对边缘MOS的多晶硅和有源区的重叠宽度d=0.5 μm,主MOS的沟道宽度W=1 μm,长度L分别为0.5、0.8、1、1.2、1.5 μm的5种Dog Bone栅MOS管结构进行仿真,并计算其等效宽长比。图 4中的黑色点线表示仿真得到的边缘MOS的等效宽长比与主MOS的长度的关系。对该曲线进行了两参数的线性倒数函数的拟合(图 4中的红色虚线),拟合公式为
| $ \frac{{W'}}{{L'}} = \frac{1}{{\alpha + \beta L}}, $ | (3) |
|
图 4 边缘MOS的等效宽长比和主MOS的长度之间关系 |
式中:L为主MOS的沟道长度,α、β为拟合参数,拟合值α=0.829 7,β=1.895 1/μm。可见,边缘MOS等效宽长比与主MOS的沟道长度成反比。
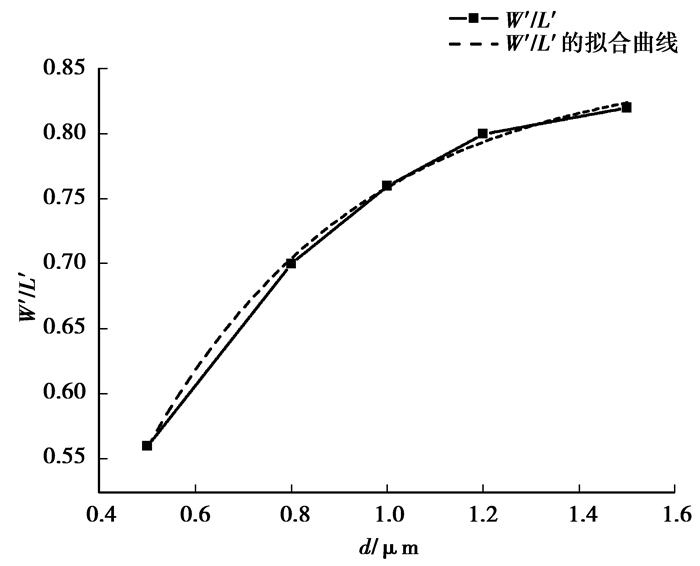
3) 边缘MOS中的多晶硅和有源区的重叠宽度d对其等效宽长比的影响。用ATLAS对主MOS的宽度沟道W=1 μm,长度L=0.5 μm,边缘MOS中的参数d分别为:0.5、0.8、1、1.2、1.5 μm的5种Dog Bone栅MOS结构进行仿真,并计算其等效宽长比。图 5是边缘MOS的等效宽长比和参数d之间的关系,其中黑色的点线表示仿真结果。对该曲线进行了指数衰减函数拟合(图中的红色虚线),拟合公式为
| $ \frac{{W'}}{{L'}} = A - {B_{\exp }}\left( {\frac{{ - d}}{C}} \right), $ | (4) |
|
图 5 边缘MOS的等效宽长比和参数d之间的关系 |
式中:d为边缘MOS的多晶硅和有源区的重叠宽度,A、B、C为拟合参数,拟合值A=0.855 3,B=0.911 0,C=0.445 1 μm。可见,边缘MOS的等效宽长比与其多晶硅和有源区的重叠宽度d成指数非线性关系。这与普通的MOS管的宽长比和多晶硅宽度成正比的特性不相同,因为边缘MOS的沟道横向电场并非一族平行电场线,而是从主MOS的漏端侧向到源端侧向的弯曲电场线,其电场强度随距离而变化,靠近主MOS的边缘处电场强,远离主MOS的边缘处则电场弱。边缘MOS沟道内横向电场线弯曲的情况也可由图 2中的边缘电流密度的分布看出。
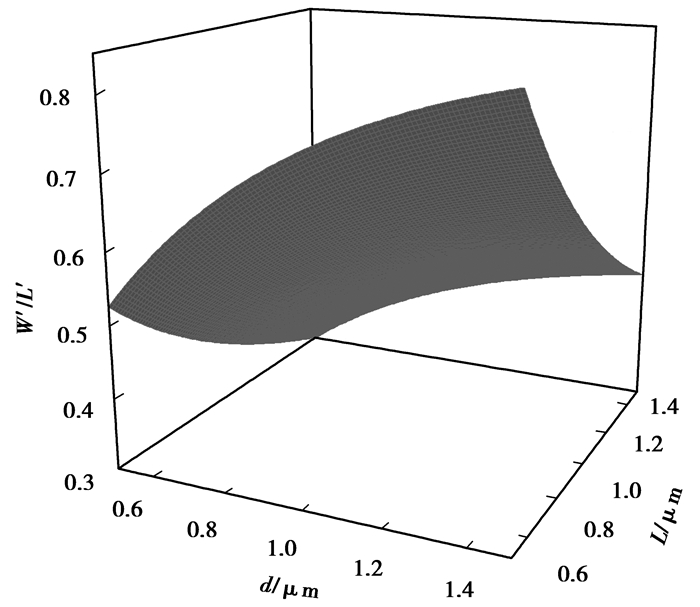
由以上仿真结果可知,边缘MOS等效宽长比与参数d和主MOS的沟道长度L有关,而与主MOS的沟道宽度W无关。因此其等效宽长比的计算式是关于d和L的函数。为了得到该两变量的函数,对更多Dog Bone栅MOS结构进行了仿真。包括:主MOS宽度W=1 μm,长度L分别为0.5、0.8、1、1.2、1.5 μm,边缘MOS的参数d分别为0.5、0.8、1、1.2、1.5 μm的总共25种Dog Bone栅MOS结构。图 6是边缘MOS等效宽长比和重叠宽度d、主MOS的沟道长度L之间的关系的拟合曲面,拟合式为
| $ \frac{{W'}}{{L'}} = = \frac{{\rho (1 - \exp ( - \theta {d})}}{{\gamma + L}}, $ | (5) |
|
图 6 边缘MOS等效宽长比和参数d、主MOS的长度L之间的关系的拟合曲面 |
式中:ρ、θ、γ为拟合参数,拟合值ρ=1.234 2,θ=1.699 5/μm,γ=0.843 4。将式(5) 代式(1) 中得到整个Dog Bone栅MOS晶体管的等效宽长比。
3 实验测试采用CSMC 0.5 μm DPTM CMOS混合信号工艺对样管进行了流片。每组测试芯片上分别有3个不同宽长比的普通结构晶体管(分别编号1、2、3) 和3个相应的Dog Bone栅MOS晶体管。1号晶体管W/L=1.1 μm/1 μm,2号晶体管W/L=2 μm/0.55 μm,3号晶体管W/L=9 μm/0.6 μm。相应Dog Bone栅MOS场效应晶体管的版图结构中,主MOS管W/L与普通晶体管的尺寸一样,边缘MOS的多晶硅和有源区的重叠宽度d不同,分别为1号d=0.75 μm,2号d=0.3 μm,3号d=0.35 μm。
用安捷伦4 155 B半导体测试仪对15组芯片进行了测试,每个样管的电流均取自饱和区处的3个点(Vgs=3 V,Vds=1.6 V;Vgs=4 V,Vds=1.6 V;Vgs=5 V,Vds=1.6 V)的电流值。
因为MOS管的电流与其等效宽长比成正比,所以在相同的工艺和电压偏置条件下,任意2个MOS管应满足关系
| $ \frac{{{I_1}}}{{{I_2}}} = \frac{{{{({W}{\rm{/}}{L})}_1}}}{{{{({W}{\rm{/}}{L})}_2}}}。$ | (6) |
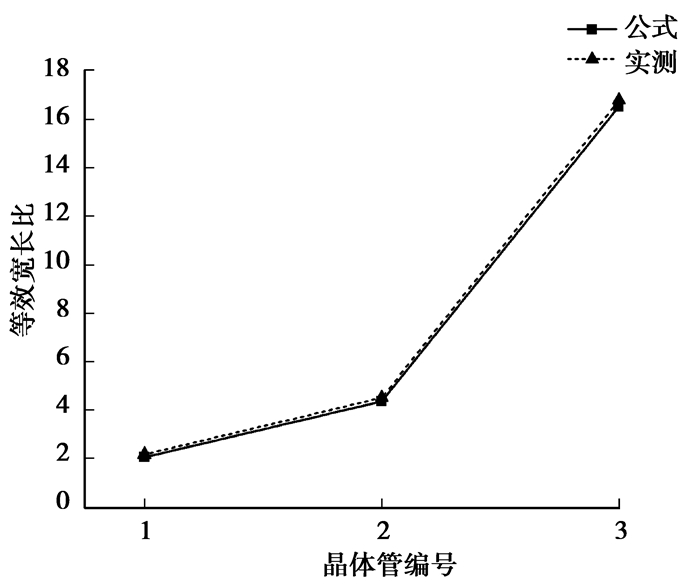
把Dog Bone栅MOS场效应晶体管的电流与普通的MOS结构的电流相比较,就得到其等效宽长比。每一个电流取值点可以得到1个等效宽长比,把这些等效宽长比取平均作为每个Dog Bone栅MOS晶体管的等效宽长比,再把15组里相同结构的Dog Bone栅MOS晶体管的等效宽长比取平均作为其最终等效宽长比。图 7所示是3个Dog Bone栅MOS结构等效宽长比的实验测量值和公式计算值的对比,由图可见,得出的拟合和实验吻合较好。
|
图 7 Dog Bone MOS等效宽长比的实验测量值和公式给出值之间的比较 |
Dog Bone MOS FET是一种防辐射总剂量效应的版图结构,与环状栅的版图结构相比,它的设计灵活、结构对称。研究借助工艺与器件仿真工具SILVACO TCAD构造了该结构晶体管的器件仿真模型,提出一种简化计算方法,把Dog Bone结构MOS划分为常规结构的主MOS和非常规的边缘MOS的并联。主MOS的宽长比可以直接从版图尺寸中的获得;计算边缘MOS的等效宽长比就可得到整个Dog Bone MOS的等效宽长比和跨导等信息。仿真结果表明,边缘MOS的等效宽长比与主MOS沟道宽度W无关,与主MOS沟道长度L成反比,与其自身的多晶硅与有源区的重叠宽度d成指数非线性关系。用拟合的方法得到了边缘MOS晶体管等效宽长比的计算公式,进而可计算得到整个Dog Bone MOS FET的等效宽长比和跨导。采用CSMC 0.5 μm DPTM CMOS混合信号工艺制作了样管,对实验测量值和公式计算值进行了比较,Dog Bone MOS晶体管的等效宽长比的计算公式与实验吻合较好。
| [1] | Oldham T R, J r, McLean F B. Total ionizing dose effects in MOS oxides and devices[J]. IEEE Transactions on Nuclear Science, 2003, 50(3): 483–499. DOI:10.1109/TNS.2003.812927 |
| [2] | Hass K J, Ambles J W. Single event transients in deep submicron CMOS[C]//Proceedings of the 199242nd Midwest Symposium on Circuits and Systems, August 8-11, 1999, Las Cruces, NM. Piscataway:IEEE Press, 1999, 1:122-125. |
| [3] | Amusan O A, Massengill L W, Baze M P, et al. Single event upsets in deep-submicrometer technologies due to charge sharing[J]. IEEE Transactions on Device and Materials Reliability, 2008, 8(3): 582–589. DOI:10.1109/TDMR.2008.2000892 |
| [4] | Baze M P, Büchner S P, McMorrow D. A digital CMOS design technique for SEU hardening[J]. IEEE Transactions on Nuclear Science, 2000, 47(6): 2603–2608. DOI:10.1109/23.903815 |
| [5] | Snoeys W, Faccio F, Burns M, et al. Layout techniques to enhance the radiation tolerance of standard CMOS technologies demonstrated on a pixel detector readout chip[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment, 2000, 439(2/3): 349–360. |
| [6] | Lacoe R C. Improving integrated circuit performance through the application of hardness-by-design methodology[J]. IEEE Transactions on Nuclear Science, 2008, 55(4): 1903–1925. DOI:10.1109/TNS.2008.2000480 |
| [7] | Mayer D C, Lacoe R C, King E E, et al. Reliability enhancement in high-performance MOSFETs by annular transistor design[J]. IEEE Transactions on Nuclear Science, 2004, 51(6): 3615–3620. DOI:10.1109/TNS.2004.839157 |
| [8] | Champion C L. Modeling of FETs with abnormal gate geometries for radiation hardening[D]. Washington:Washington State University, 2004. http://www.eecs.wsu.edu/~dheo/deuk_cv_Feb2007_web.pdf |
| [9] | Silvaco International. Atlas user's manual:version 5.10.0.R[CP]. Santa Clara:Silvaco International Corporation, 2005. http://perso.esiee.fr/~polleuxj/Documents/athena_users.pdf |
 2013, Vol. 36
2013, Vol. 36

