图像融合是指对多个图像传感器获得的互补或冗余信息进行集合的过程。它使得新图像更加适合人的视觉感知,或者满足诸如图像处理中的分割、特征提取、目标识别的需要[1]。图像融合技术现已广泛应用于军事[2]、遥感[3]、医学[4]和安防[5]等众多领域。
红外与可见光图像传感器在军事、安防领域的用途广泛。红外图像能较好地反映与背景温差较大的目标,但是对于细节部分表现得不明显;可见光图像可较好地反映场景的细节,但在照度不佳时对比度较低[6]。红外与可见光图像的融合能够将红外图像中目标存在特性和可见光图像中丰富的背景信息相结合,有效地综合和发掘它们各自的特征信息,增强场景理解,突出目标。
Piella[7]提出了一个通用的多分辨率图像融合框架。基于多分辨率分析的图像融合方法能较好地挖掘被融合图像的互补信息,得到更符合人类视觉特性的融合效果[8]。刘刚等[9]将拉普拉斯金字塔(laplacian pyramid, LP)应用于图像融合,但是拉普拉斯金字塔变换会产生大量的冗余信息,且不能很好地体现原始图像的方向信息。晁锐等[10]将小波变换(wavelet transform, WT)应用于图像融合,小波变换具有非冗余和方向性的优点,但是小波变换缺乏平移不变性,不可避免地在融合后图像的尖锐边缘附近的局部区域引入振铃和抖动。平稳小波变换[11](stationary wavelet transform, SWT)具有平移不变性,能克服小波变换在图像融合中存在的振铃效应,有利于提升图像融合效果。
对于大多数图像融合的应用来说,更有意义的是将各种源图像中的目标信息融合而不是简单的像素融合[12],因此将目标信息引入到融合过程是非常必要的。
为此,笔者提出一种基于图像分割和平稳小波变换的红外与可见光图像融合方法,首先运用图像分割方法将红外图像分割为背景部分和目标部分;然后利用平稳小波变换将红外图像的背景部分与可见光图像进行融合;最后对该融合结果与红外图像的目标部分采用加权求和的融合准则进行融合,得到最终的红外与可见光融合图像。
1 结合最大类间方差和边缘检测的红外图像分割方法图像分割是指将图像划分为若干具有特征一致性且相互不重叠的区域的过程[13]。红外图像可以较好地反映与背景温差较大的目标,目标部分的灰度值通常较大,因此利用最大类间方差方法(Otsu方法)[14]可以将红外图像分割为目标部分和背景部分,但是Otsu方法存在一个明显的缺点,即它倾向于将图像分割成2个大小相当的部分而不管目标和背景的实际大小。研究提出一种结合最大类间方差和边缘检测的红外图像分割方法,该方法能够比较准确的分离出目标和背景部分,较好地保留目标图像的边缘轮廓特征。
1.1 Otsu方法Otsu方法在类间方差最大的情况下是最佳的,且完全以在一幅图像的直方图上执行计算为基础,便于计算。设输入图像有L个灰度级,它们分别为[0, 1, ……, L-1],研究的基本步骤如下[14]
1) 计算输入图像每个灰度级i出现的概率pi(i=0, 1, ……, L-1);
2) 对每个灰度级k(k=0, 1, ……, L-1),计算累积和
3) 对每个灰度级k(k=0, 1, ……, L-1),计算累积均值
4) 计算图像的全局灰度均值
5) 对每个灰度级k(k=0, 1, ……, L-1),计算类间方差
6) 得到使σB2(k)最大的k值,即为Otsu阈值k*,如果最大值不唯一,用相应检测到的各个最大值k的平均得到k*。
1.2 Canny边缘检测方法基本步骤如下[15]
1) 用一个高斯滤波器平滑输入图像;
2) 计算梯度幅值图像和角度图像;
3) 对梯度幅值图像应用非最大抑制;
4) 用双阈值处理和连接分析来检测并连接边缘。
1.3 结合Otsu和Canny边缘检测的红外图像分割方法为克服Otsu方法倾向于将图像分割成2个大小相当的部分而不管目标和背景的实际大小的缺陷,笔者将Otsu和Canny边缘检测结合起来,利用Otsu计算目标阈值,利用Canny边缘检测计算得到可能的目标区域,最后综合两者信息以判定目标区域,其算法的具体步骤如下
1) 利用Otsu方法得到红外图像目标分割的阈值k*;
2) 利用Canny边缘检测方法得到红外图像可能的目标区域的边缘,计算这些边缘内部区域的均值Mean;
3) 对于由步骤2) 得到的可能的目标区域,比较其均值Mean和k*的大小,如果Mean>k*,则对应的区域为目标区域;否则为背景区域。
通过上述步骤将红外图像分割为目标图像与背景图像。
2 基于平稳小波变换的图像融合方法 2.1 小波变换与平稳小波变换小波变换具有良好的时频局域化特性和多分辨率特性,在图像融合中得到了广泛的应用。基于多分辨率分析理论,Mallat[16]给出了小波变换的快速算法,其分解和重构实质是低通和高通滤波过程,且分解需要进行下采样,重构需要进行上采样。由于存在采样操作,小波变换不具备平移不变性,这将导致融合图像出现相位失真而产生振铃效应等问题。
为了克服小波变换不具备平移不变性的问题,Nason等[11]提出了平稳小波变换。平稳小波变换与小波变换的分解策略是相同的,唯一的区别在于:在分解过程中不进行下采样,从而具备了平移不变性。此外,在分解过程中为了满足奈奎斯特采样定理,需要对滤波器在奇位置或偶位置进行插零上采样。平稳小波变换能克服在图像融合中存在的振铃效应和光谱失真,有利于提升图像融合效果。
设用于分解的小波低通滤波器为h(n),高通滤波器为g(n),对于第j层的低通滤波器和高通滤波器,每2个系数之间内插2j-1个零来实现对滤波器的扩展,即
| $ {h^{({j})}}({k}) = \left\{ \begin{array}{l} h\left( {\frac{k}{{{2^j}}}} \right), k = {2^j}m, m \in Z;\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else, }} \end{array} \right. $ | (1) |
| $ {g^{({j})}}({k}) = \left\{ \begin{array}{l} g\left( {\frac{k}{{{2^j}}}} \right), k = {2^j}m, m \in Z;\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else, }} \end{array} \right. $ | (2) |
二维平稳小波变换的分解公式如下
| $ {A^{({j})}}({m, n}) = {\sum\limits_{k, l} h ^{({j})}}({k}){h^{({j})}}({l}){A^{({j - {\rm{1}}})}}({k + m, l + n}); $ | (3) |
| $ {H^{({j})}}({m, n}) = {\sum\limits_{k, l} g ^{({j})}}({k}){h^{({j})}}({l}){A^{({j - {\rm{1}}})}}({k + m, l + n}); $ | (4) |
| $ {V^{({j})}}({m, n}) = {\sum\limits_{k, l} h ^{({j})}}({k}){{g}^{({j})}}({l}){A^{({j - {\rm{1}}})}}({k + m, l + n}); $ | (5) |
| $ {D^{(j)}}(m,n) = \sum\limits_{k,l} {{g^{(j)}}} (k){g^{(j)}}({l}){A^{(j - 1)}}(k + m,l + n); $ | (6) |
其中,A(j-1)表示原始图像在尺度2j-1下的低频近似,A(j)表示原始图像在尺度2j下的低频近似,H(j)、V(j)、D(j)分别表示原始图像在尺度2j下的水平方向、垂直方向和对角方向的高频细节。
设用于重构的小波低通滤波器为
| $ {{{\tilde h}}^{({j})}}({k}) = \left\{ \begin{array}{l} {\tilde h}\left( {\frac{k}{{{2^j}}}} \right), k = {2^j}m, m \in Z;\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else, }} \end{array} \right. $ | (7) |
| $ {{\tilde g}^{({j})}}({k}) = \left\{ \begin{array}{l} \tilde g\left( {\frac{k}{{{2^j}}}} \right), k = {2^j}m, m \in Z;\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else, }} \end{array} \right. $ | (8) |
二维平稳小波变换的重构公式如下
| $ \begin{array}{l} \;\;{A^{({j - }{\rm{1}})}}({m, n}) = \frac{1}{4}\left[{\sum\limits_{k, l} {{{{\tilde h}}^{({j})}}} ({k}){{\tilde h}^{({j})}}({l}){A^{({j})}}({k + }} \right.\\ {m, l + n}) + \sum\limits_{k, l} {{{\tilde g}^{({j})}}({k}){{\tilde h}^{({j})}}({l}){{H}^{({j})}}({k + m, l + n})} + \\ \;\;\;\;\;\;\;\;\sum\limits_{k, l} {{{{\tilde h}}^{({j})}}({k}){{\tilde g}^{({j})}}({l}){{V}^{({j})}}({k + m, l + n}) + } \\ \;\;\;\;\;\;\;\left. {\sum\limits_{k, l} {{{\tilde g}^{({j})}}({k}){{\tilde g}^{({j})}}({l}){{D}^{({j})}}({k + m, l + n})} } \right]。\end{array} $ | (9) |
经平稳小波变换后,源图像被分解为低频子带和高频子带。低频子带主要包含源图像的近似特性,反映图像的轮廓等信息;高频子带主要包含源图像的细节特性,反映图像的纹理、边缘等信息。
图像融合准则的选择对于融合质量至关重要。目前广为采用的融合准则可概括为基于像素和基于区域特征的融合准则,针对图像低频子带和高频子带不同特点,应选择与之相适应的融合准则。
1) 图像低频子带融合准则
图像的低频子带主要包含源图像的近似特性,占据图像的主要能量。常见低频子带融合准则有平均法[17],区域能量取大法[18]和区域方差取大法[19]等。但是,平均法没有考虑图像的边缘和亮度特征,降低了融合图像的对比度,影响融合图像的视觉效果;区域能量取大法倾向于选择高亮度区域,会细化低亮度区域边缘;区域方差取大法会优先选择边缘纹理丰富的区域,忽视亮度的影响,且对噪声比较敏感。为此,低频子带的融合准则采用区域空间频率取大的方法。
图像的区域空间频率定义[20]如下
| $ BF = \sqrt {\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 2}^N {[{F}{\rm{(}}{i, j}{\rm{)-}}{F}{{{\rm{(}}{i, j-}{\rm{1)}}}^2}]} } } ; $ | (10) |
| $ CF = \sqrt {\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 2}^N {[{F}{\rm{(}}{i, j}{\rm{)-}}{F}{{{\rm{(}}{i-}{\rm{1}}{, j}{\rm{)}}}^2}]} } } ; $ | (11) |
| $ SF = \sqrt {R{F^2} + C{F^2}} , $ | (12) |
其中RF为空间行频率(row frequency),CF为空间列频率(column frequency),SF为空间频率,F(i, j)表示图像在(i, j)处的灰度值,M、N表示图像区域的大小。空间频率[21]反映了图像的边缘化程度,能很好地描述图像的灰度突变信息,空间频率越大图像就越活跃、越清晰。融合准则选择区域空间频率取大法有利于提高融合图像的边缘细节信息和清晰度,其系数选取准则如下
| $ {C^F}{\rm{(}}{i, j}{\rm{) = }}\left\{ \begin{array}{l} {C^A}{\rm{(}}{i, j}{\rm{)}}, {S}{{F}^A}{\rm{(}}{i, j}{\rm{)}} \ge {S}{{F}^B}{\rm{(}}{i, j}{\rm{);}}\\ {C^B}{\rm{(}}{i, j}{\rm{), otherwise, }} \end{array} \right. $ | (13) |
其中:CF(i, j)表示融合图像低频系数;CA(i, j)表示源图像A的低频系数;CB(i, j)表示源图像B的低频系数;SFA(i, j)表示源图像A在(i,j)处的区域空间频率;SFB(i, j)表示源图像B在(i,j)处的区域空间频率。
2) 图像高频子带融合准则
图像的高频子带主要包含源图像的细节特性,反映图像的纹理、边缘等信息;且平稳小波变换后图像高频子带的数据量较小波变换大大增加。为此,高频子带的融合准则采用绝对值取大法,即选择取绝对值较大的高频分量作为融合图像的高频分量, 既能够得到边缘细节较丰富、清晰度较高的融合图像,又可以节约图像融合所花的时间,提高图像融合速度。
2.3 基于平稳小波变换的图像融合方法采用的基于平稳小波变换的图像融合方法如下
1) 利用研究方法对源图像分别进行平稳小波变换,得到各自的低频子带和高频子带;
2) 利用区域空间频率取大法和绝对值取大法分别对源图像的低频子带和高频子带进行融合,得到融合后图像的低频和高频子带;
3) 将融合后图像的低频和高频子带进行平稳小波逆变换得到最终的融合图像。
3 基于图像分割和平稳小波变换的红外与可见光图像融合方法笔者提出一种基于图像分割和平稳小波变换的红外与可见光图像融合方法,如图 1所示
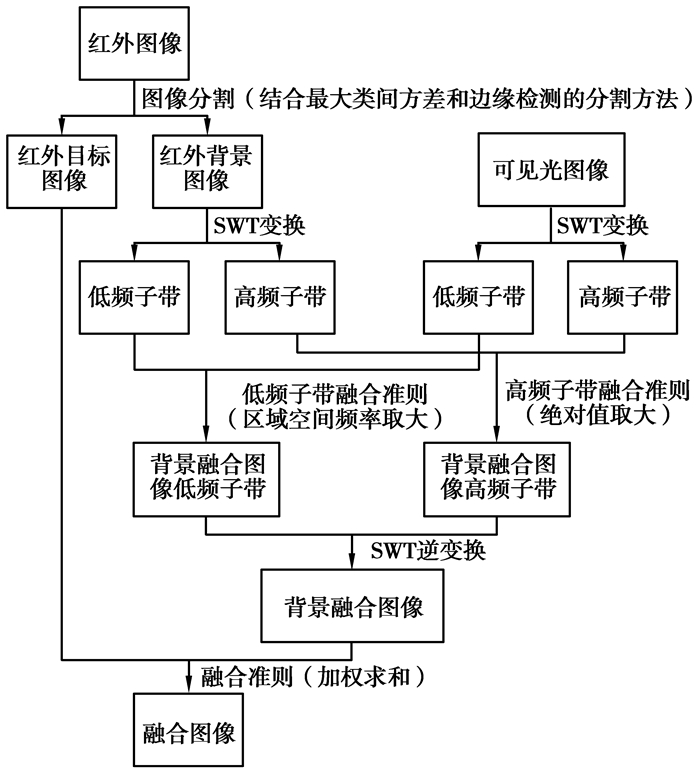
|
图 1 基于图像分割和平稳小波变换的红外与可见光图像融合方法算法流程 |
其中SWT表示平稳小波变换,所使用的加权求和融合准则如下
| $ {F}{\rm{(}}{i, j}{\rm{)}} = {w_1}IR\_O({i}{\rm{, }}{j}) + {w_2}B({i}{\rm{, }}{j}), $ | (14) |
其中:F(i, j)表示融合图像;IR_O(i, j)表示红外目标图像;B(i, j)表示背景融合图像,w1,w2表示权重系数。
4 实验结果与分析 4.1 图像融合评价方法图像融合的质量评价方法主要可分为2类:主观评价方法和客观评价方法。主观评价方法就是依靠人眼对融合图像效果进行主观判断的方法,其优点是简单、直观。客观评价方法依据模型给出的量化指标来衡量融合图像质量,本论文采用标准差、信息熵和互信息[22]3个评价指标来进行客观评价。
1) 标准差
标准差是由均值间接求得的,其定义为
| $ {\rm{std}} = \sqrt {\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{({F}{\rm{(}}{i, j}{\rm{) - }}\mu {\rm{)}}}^2}} } }, $ | (15) |
其中F(i, j)表示图像在(i, j)处的灰度值,M, N表示图像的尺寸,μ表示图像的均值。标准差反映了图像灰度值相对于图像灰度均值的离散程度情况,标准差越大,则灰度级分布就越分散,图像的对比度也就越大,图像融合效果越好。
2) 信息熵
根据香农理论,熵的定义为
| $ {H = - }\sum\limits_{i = 0}^{l - 1} P {\rm{(}}{i}{\rm{)log}}{P}{\rm{(}}{i}{\rm{)}}, $ | (16) |
其中:l为图像总的灰度级数,P(i)是灰度值为i的像素数Ni与图像总像素数之比,即
3) 互信息
互信息量的定义为
| $ MI = H({A}) + H({B}) - H({AB}), $ | (17) |
其中:H(A)为源图像A的熵;H(B)为源图像B的熵;H(AB)为源图像A、B的联合熵;其定义为
| $ H({AB}) = - \sum\limits_i {\sum\limits_j {P({{A}_i}{{B}_j})} } {\rm{log}}{P}({{A}_i}{{B}_j})。$ | (18) |
融合图像与2个源图像的互信息为
| $ {\rm{MI}} = {\rm{M}}{{\rm{I}}_{AF}} + {\rm{M}}{{\rm{I}}_{BF}}。$ | (19) |
其中F为融合后图像。互信息量可作为2个或多个变量之间相关性的度量,这里衡量融合图像与源图像的关联程度。互信息量的值越大,表明融合图像从源图像中所获取的信息越多,融合效果越好。
4.2 图像融合实验结果与分析为了验证所提出方法的有效性,选择基于Laplacian塔变换的图像融合方法(LPTF),基于小波变换的图像融合方法(WTF)和基于平稳小波变换的图像融合方法(SWTF)与提出的方法进行对比。其中,LPTF的分解层数为4层,低频融合准则为均值法,高频融合准则为绝对值取大法;WTF所使用的小波基为bior 4.4小波,分解层数为4层,低频融合准则为均值法,高频融合准则为绝对值取大法;SWTF所使用的小波基为bior4.4小波,分解层数为4层,低频融合准则其一为均值法(SWTF1),其二为区域频率取大法(SWTF2),高频融合准则为绝对值取大法;研究提出的方法所使用的小波基为bior4.4小波,分解层数为4层,权重系数w1=1.0,w2=1.0。采用标准差、信息熵和互信息3个评价指标来进行客观评价。实验采用的红外与可见光图像来源于荷兰TNO Human Factors Research Institute拍摄的“UN Camp”红外和可见光序列图,第一组图像序号为“1815”,第二组图像序号为“1831”。融合图像结果分别如图 2和图 3所示,评价指标结果如表 1所示。
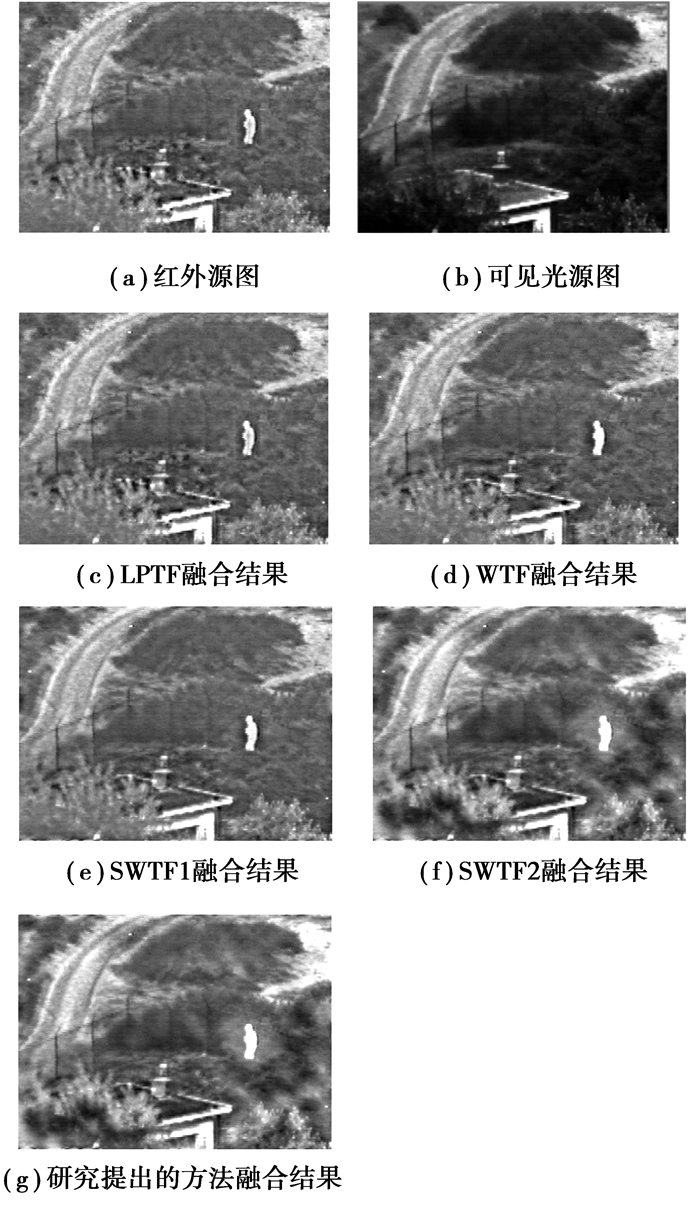
|
图 2 源图像(1815) 及不同方法的融合结果 |
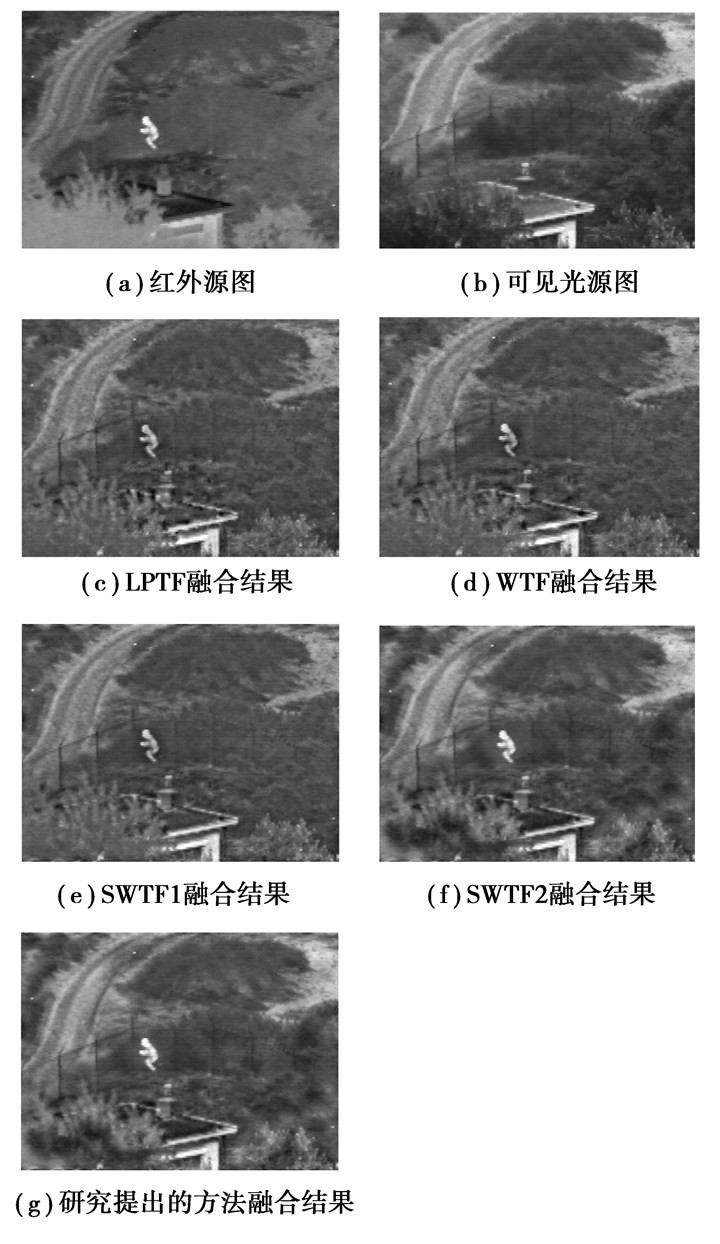
|
图 3 源图像(1831) 及不同方法的融合结果 |
| 表 1 图像融合结果客观评价指标 |
LPTF、WTF和SWTF1的融合图像整体对比度不高,亮度较暗,图像目标人物特征比较模糊,而且可见光图像的道路、栏杆等重要信息没有很好地在融合图像中体现出来;而SWTF2和融合算法得到的融合图像既能有效突出目标,又能较好地反映道路、栏杆等细节信息。
从表 1可以得出如下结论
1) 融合算法得到的融合图像的标准差、信息熵、互信息均为最高,这说明融合图像的对比度更高、信息量更丰富、从源图像中所获取的信息更多,融合算法的融合效果优于其它方法;
2) SWTF2得到的融合图像的标准差、信息熵、互信息要比SWTF1的高,这说明采用SWTF2得到的融合图像的对比度更高、信息量更丰富、从源图像中所获取的信息更多,SWTF2的融合效果优于SWTF1,即在低频子带采用区域空间频率取大融合准则的融合效果要优于均值法。
5 结论提出一种基于图像分割和平稳小波变换的红外与可见光图像融合方法。该方法首先结合Otsu和Canny边缘检测的红外图像分割方法将红外图像分割为目标图像和背景图像;然后利用基于平稳小波变换的图像融合方法将红外背景图像与可见光图像进行融合,其中低频部分采用区域空间频率取大融合准则,高频部分采用绝对值取大融合准则,得到背景融合图像;最后利用加权求和融合准则将背景融合图像与红外目标图像相融合,得到最终的红外与可见光融合图像。实验结果表明,所提出的融合方法不仅很好地突出了红外图像的目标信息,还较好地体现了可见光图像的场景细节信息,很好地改善了融合图像的视觉效果。无论是在视觉效果上,还是在标准差、信息熵和互信息的客观指标上均优于拉普拉斯金字塔变换和小波变换等传统的融合算法。
| [1] | Pohl C, Van GENDEREN J L. Multisensor image fusion in remote sensing:concepts, methods and applications[J]. International Journal of Remote Sensing, 1998, 19(5): 823–854. DOI:10.1080/014311698215748 |
| [2] | Muller A C, Narayanan S. Cognitively-engineered multisensor image fusion for military applications[J]. Information Fusion, 2009, 10(2): 137–149. DOI:10.1016/j.inffus.2008.08.008 |
| [3] | Dixon T D, Nikolov S G, Lewis J J, et al. Task-based scanpath assessment of multisensor video fusion in complex scenarios[J]. Information Fusion, 2010, 11(1): 51–65. DOI:10.1016/j.inffus.2009.04.007 |
| [4] | Kumar M, Dass S. A total variation-based algorithm for pixel-level image fusion[J]. IEEE Transactions on Image Processing, 2009, 18(9): 2137–2143. DOI:10.1109/TIP.2009.2025006 |
| [5] | Sadler J, Smith M I. Enhancing image fusion performance and utility for defence and security applications[J]. Proceedings of the SPIE, 2009, 7345: 1–13. |
| [6] | Schmidt R. Benefits of ir/visible fusion[J]. Proceedings of the SPIE, 2007, 654105: 1–6. |
| [7] | Piella G. A general framework for multiresolution image fusion:from pixels to regions[J]. Information Fusion, 2003, 4(4): 259–280. DOI:10.1016/S1566-2535(03)00046-0 |
| [8] | Donoho D L, Flesia A G. Can recent innovations in harmonic analysis 'explai' key findings in natural image statistics[J]. Network:Computation in Neural Systems, 2001, 12(3): 371–393. DOI:10.1080/net.12.3.371.393 |
| [9] | Liu Gang, Jing Z L, Sun S Y, et al. Image fusion based on expectation maximization algorithm and steerable pyramid[J]. Chinese Optics Letters, 2004, 2(7): 386–389. |
| [10] |
晁锐, 张科, 李言俊.
一种基于小波变换的图像融合算法[J]. 电子学报, 2004, 32(5): 750–753.
CHAO Rui, ZHANG Ke, LI Yinjun. A image fusion method based on wavelet transform[J]. Chinese Journal of Electronics, 2004, 32(5): 750–753. (in Chinese) |
| [11] | Nason G P, Silverman B W. The stationary wavelet transform and some statistical applications in wavelet and statistics[J]. Lecture Notes in Statistics, 1995, 103: 281–299. DOI:10.1007/978-1-4612-2544-7 |
| [12] | Plella G. A region-based multiresolution image fusion algorthim[C]//Proceedings of the Fifth International Conference on Information Fusion, 2002, 2(2):1557-1564. |
| [13] | Pal N R, Pal S K. A review on image segmentation techniques[J]. Patten Recognition, 1993, 26(9): 1277–1294. DOI:10.1016/0031-3203(93)90135-J |
| [14] | Otsu N. A threshold selection method from a gray level histograms[J]. IEEE Transactions Systems, 1979, SMC-9: 62–66. |
| [15] | Canny J. A computational approach to edge detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679–698. |
| [16] | Mallat S. A theory for multiresolution signal decomposition:the wavelet representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674–693. DOI:10.1109/34.192463 |
| [17] |
张强, 郭宝龙.
一种基于Curvelet变换多传感器图像融合算法[J]. 光电子激光, 2006, 17(9): 1123–1127.
ZHANG Qiang, GUO Baolong. Fusion of multisensor images based on the Curvelet transform[J]. Journal of Optoelectronics Laser, 2006, 17(9): 1123–1127. (in Chinese) |
| [18] |
叶传奇, 苗启广, 王宝树.
基于非子采Contourle变换的图像融合方法[J]. 计算机辅助设计与图形学学报, 2007, 19(10): 1274–1278.
YE Chuanqi, MIAO Qiguang, WANG Baoshu. Image fusion method based on the nonsubsampled contourlet transform[J]. Journal of Computer-Aided Design & Computer Graphics, 2007, 19(10): 1274–1278. (in Chinese) |
| [19] |
杨镠, 郭宝龙, 倪伟.
基于区域特性的Contourlet域多聚焦图像融合算法[J]. 西安交通大学学报, 2007, 41(4): 448–452.
YANG Liu, GUO Baolong, NI wei. Multifocus image fusion algorithm based on region statistics in Contourlet domain[J]. Journal of Xi'An Jiao Tong University, 2007, 41(4): 448–452. DOI:10.7652/xjtuxb200704015 (in Chinese) |
| [20] | Eskicioglu A M, Fisher P S. Image quality measures and their performance[J]. IEEE Transactions on Communications, 1995, 12(43): 2959–2965. |
| [21] | Pajares G, Cruz J M. A wavelet-based image fusion tutorial[J]. IEEE Pattern Recognition, 2004, 37(9): 1855–1872. DOI:10.1016/j.patcog.2004.03.010 |
| [22] |
杨晓慧, 金海燕, 焦李成.
基于DT-CWT的红外与可见光图像自适应融合[J]. 红外与毫米波学报, 2007, 26(6): 419–424.
YANG Xiaohui, JIN Haiyan, JIAO Licheng. Aaptive image fusion algorithm for infrared and visible light images based on DT-CWT[J]. Journal of Infrared and Millimeter Waves, 2007, 26(6): 419–424. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

