设备寿命周期内的故障率分布曲线包含了设备可靠性的关键信息,是对设备进行可靠性设计、试验等可靠性工作的基础,因而研究设备故障率曲线的变化规律具有重要的理论意义和实际应用价值[1]。国内外对此做了大量研究。Rodrigo B.Silva[2]指出故障率分布曲线的形状能揭示设备的故障机理或者对应于设备特定的使用阶段,有助于故障的预测和控制。M.Xie[3]运用扩展威布尔模型建立故障率分布曲线并给出参数估计方法,为故障率曲线建模提供了新的思路和方法。李瑞莹[4]在对比多种时间序列模型的基础上,建立了故障率预测模型并给出实施步骤,为故障预测提供了理论基础。对于数控机床的故障率研究,J. A. Jones[5]提出新的故障数据搜集方法,从而为提高机床可靠性作好基础工作。Yu J[6]运用复杂寿命分布模型对加工中心寿命周期故障数据进行可靠性建模以及故障率分布模型研究。廖小波[7]在故障数据统计分析的基础上,提出了机床的故障率曲线服从浴盆分布。然而,上述文献忽略了机床是集机、电、液、气等于一体的复杂设备,仅仅应用单一分布模型建立机床故障率分布曲线。事实上,机床发生的故障是由多种原因或失效机理引起的,在不同的使用时期所发生的故障特征也不相同。同时,采用单一形式的分布拟合多样式分布会出现较大的误差[8]。因此,采用两重威布尔分段模型来拟合机床故障率分布曲线,充分考虑机床在早期故障期和偶然故障期所发生的故障是由不失效机理造成。然后对早期故障期与偶然故障期之间的时间拐点进行确定。最后运用该模型对该系列加工中心的最优保修期进行研究。
1 机床故障率曲线定量化建模 1.1 观测值分析机床故障间隔时间是用来拟合其可靠性分布模型的重要的基础数据[9]。传统的可靠性考核方法所关注的是产品在偶然故障期的故障数据,一般是在产品投入使用一年以后开始跟踪考核的,这就忽略了产品投入使用初期的故障。以某机床厂的某系列卧式加工中心为研究对象,搜集该系列5台加工中心在3个用户单位运行近一年的故障维修记录,共统计得到61个故障数据。以考核时间内的加工中心故障间隔时间观测值来拟合其概率密度函数,并将故障间隔时间观测值t∈[2, 1735]分为7组,如表 1所示。
| 表 1 加工中心整机故障频率表 |
以每组时间的中值为横坐标,每组的概率密度的观测值
| $ \mathop f\limits^ \wedge \left( t \right) = \frac{{{n_i}}}{{n\Delta {t_i}}}, $ | (1) |
式中:ni为每组故障间隔时间中的故障频数;
n为故障总频数,n=61;
Δti为组距,为247.57 h;
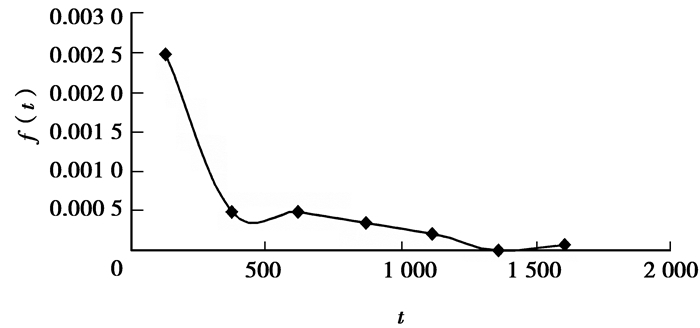
拟合出的概率密度曲线如图 1所示。
|
图 1 故障间隔时间概率密度曲线 |
由图 1可知,该加工中心故障间隔时间的概率密度曲线呈单调下降趋势,而且下降到一定时间后趋于平稳。因此,该加工中心故障间隔时间所服从的分布不会是正态分布或对数正态分布,而可能是指数分布或者威布尔分布。由于指数分布是威布尔分布的形状参数β=1时的形式[11]。因此,假设该系列加工中心故障间隔时间服从威布尔分布。
1.2 模型建立 1.2.1 威布尔分布的线性回归分析假设试验中获得n组试验数据:(x1, y1)、(x2, y2)、…、(xn, yn),将其标在直角坐标纸上。从图形上看,数据点大体上散布在一条直线的附近,变量间近似地呈现为线性关系[12]。设直线方程为
| $ y = \mathit{\boldsymbol{A}} + Bx, $ | (2) |
式中,参数B为该直线的斜率,A为截矩。
对于2参数威布尔分布,其累积分布函数为
| $ F\left( t \right) = \left\{ \begin{array}{l} \int_0^t {f\left( t \right){\rm{d}}t} = 1 - \exp \left[ { - {{\left( {\frac{{t - \gamma }}{\alpha }} \right)}^\beta }} \right],t \ge \gamma ;\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t < \gamma , \end{array} \right. $ | (3) |
式中:β为形状参数,β>0;
α为尺度参数,α>0;
γ为位置参数,γ>0;
在设备的故障分析中,β与设备的故障机理相联系,不同的β值伴随着不同的故障机理。当β>1时,呈早期故障期的寿命分布;当β=1时,呈偶然故障期的寿命分布;当β=1时,呈耗损故障期的寿命分布。α与工作条件的负载有关,负载大,则相应的α小;反之亦然。γ的变化影响概率密度曲线的平移位置,产品在t=γ之前不发生故障,在t=γ以后发生故障。
实际应用中,往往假设在t=0时产品便发生故障。这样,式(3)便简化为
| $ F\left( t \right) = 1 - \exp \left[ { - {{\left( {\frac{t}{\alpha }} \right)}^\beta }} \right],t \ge 0; $ | (4) |
两端进行线性变换,并取自然对数得
| $ \ln \left[ {\ln \left( {\frac{1}{{1 - F\left( t \right)}}} \right)} \right] = \beta \ln t - \beta \ln \alpha 。$ | (5) |
对比式(2)和式(5)
令
| $ \overset{\wedge }{\mathop{\rm{ }\mathit{y}}}\,=\overset{\wedge }{\mathop{\mathit{\boldsymbol{A}}}}\,+\overset{\wedge }{\mathop{\rm{ }B}}\,\overset{\wedge }{\mathop{\rm{ }\mathit{x}}}\,, $ | (6) |
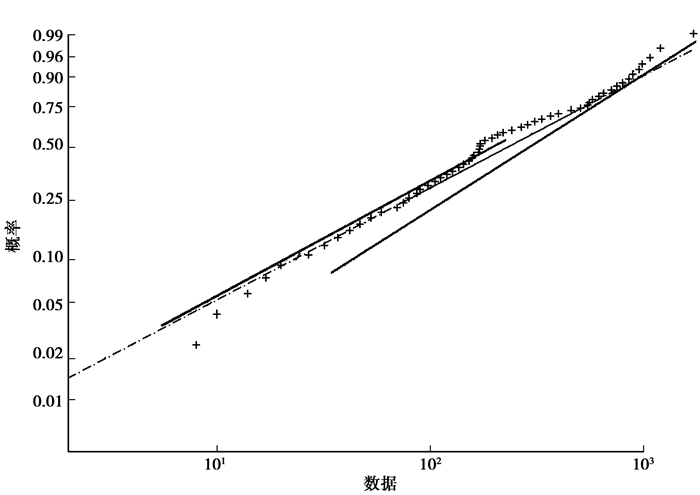
通过Matlab把搜集的故障数据进行线性化处理,得到威布尔概率图,如图 2。
|
图 2 威布尔概率图 |
从图 2中可以看出,数据点并不完全在一条直线上,而是出现拐点。所以用单一的威布尔分布去拟合该批数据是不合适的,应该用更为复杂的模型来对其进行建模;根据WPP图的形状和已知不同参数范围的WPP图相比较可知,其属于两重威布尔分段模型(β1 < β2)的情况。
1.2.2 两重威布尔分段模型建立由两重威布尔分段模型的定义[10]:
将时间t≥0的区间分为2个区间T1和T2:T1={0, t0},T2={t0, t},其模型的可靠性函数为R(t)=kiRi(t),Ri(t)是参数为βi和αi的2参数威布尔分布,若β1=β2,则模型将退化为一个简单的威布尔分布,因此令β1≠β2。由此得两重威布尔分段模型的为
| $ R\left( t \right) = \left\{ \begin{array}{l} {k_1}\exp \left[ { - {{\left( {t/{\alpha _1}} \right)}^{{\beta _1}}}} \right],0 < t \le {t_0};\\ {k_2}\exp \left[ { - {{\left( {t/{\alpha _2}} \right)}^{{\beta _2}}}} \right],{t_0} < t。\end{array} \right. $ | (7) |
说明:如果直接采用两参数威布尔分布模型组成的两重威布尔分段模型,虽然其可靠性函数在分界点处是连续的,但其密度函数和失效率函数是不连续的。为了让两重威布尔分段模型的密度函数f(t)在分界点处2段曲线达到连续,在模型中引入参数k1, k2,其几何意义是通过k1, k2调节f2(t)的上下位置达到与f1(t)的平滑对接,实现连续的目的,k1, k2的作用相当于一个权值。
1.2.3 极大似然函数估计参数设f(x;θ1,θ2,…,θm)(θ1,θ2,…,θm是m个待估参数)为随机变量X的总体概率密度,根据随机变量X的n个观测数据可构造似然函数[10]。
| $ L\left( {{\theta _1},{\theta _2}, \cdots ,{\theta _m}} \right) = \prod\limits_{i = 1}^n {f\left( {{x_i};{\theta _1},{\theta _2}, \cdots ,{\theta _m}} \right)} 。$ | (8) |
对似然函数lnL(θj) (j=1, 2, …, m)取极值,可以得到似然方程组
| $ \frac{{{\rm{dln}}L\left( {{\theta _j}} \right)}}{{{\rm{d}}{\theta _j}}} = 0, $ | (9) |
求解式(9) 即可求得参数θj的估计值。
从图 2可得,前29个点拟合成直线L1;而由后31个点拟合成渐近线L2。因此可以对两重威布尔分段模型参数分段进行极大似然估计。两参数威布尔分布的似然函数可以写成为
| $ \begin{array}{*{20}{c}} {\ln \left[ {L\left( \theta \right)} \right] = }\\ {n\ln \left( \beta \right) - n\beta \ln \left( \alpha \right) + \left( {\beta - 1} \right)\ln \left( {\sum\limits_{i = 1}^n {{t_i}} } \right) - \sum\limits_{i = 1}^n {{{\left( {\frac{{{t_i}}}{\alpha }} \right)}^\beta }} 。} \end{array} $ | (10) |
求偏微分并令其为零得
| $ \begin{array}{*{20}{c}} {\frac{{\partial \ln \left[ {L\left( \theta \right)} \right]}}{{\partial \beta }} = }\\ {\frac{n}{\beta } - n\ln \left( \alpha \right) + \left( {\sum\limits_{i = 1}^n {{t_i}} } \right) - \sum\limits_{i = 1}^n {{{\left( {\frac{{{t_i}}}{\alpha }} \right)}^\beta }} \ln \left( {\frac{{{t_i}}}{\alpha }} \right) = 0。} \end{array} $ | (11) |
| $ \frac{{\partial \ln \left[ {L\left( \theta \right)} \right]}}{{\partial \alpha }} = \frac{{ - n\beta }}{\alpha } + \sum\limits_{i = 1}^n {{{\left( {\frac{{{t_i}}}{\alpha }} \right)}^\beta }} \frac{\beta }{\alpha } = 0。$ | (12) |
由式(11) 和式(12) 可得
| $ \left\{ \begin{array}{l} \alpha = {\left[ {\frac{{\sum\limits_{i = 1}^n {t_i^\beta } }}{n}} \right]^{\frac{1}{\beta }}}\\ \frac{n}{\beta } - n\ln \left( \alpha \right) + \left[ {\sum\limits_{i = 1}^n {\ln \left( {{t_i}} \right)} } \right] - \frac{1}{{{\alpha ^\beta }}}\sum\limits_{i = 1}^n {t_i^\beta \ln \left( {\frac{{{t_i}}}{\alpha }} \right)} = 0 \end{array} \right.。$ | (13) |
式(13) 中n为失效数据个数,ti代表故障间隔时间;通过迭代求解式(13) 的极大似然估计值。
| $ {\beta _1} = 0.894,{\alpha _1} = 331,{\beta _2} = 1.014,{\alpha _2} = 445, $ | (14) |
将式(14) 代入式(7) 可得
| $ R\left( t \right) = \left\{ \begin{array}{l} {k_1}\exp \left[ { - {{\left( {t/331} \right)}^{0.894}}} \right],0 < t \le {t_0};\\ {k_2}\exp \left[ { - {{\left( {t/445} \right)}^{1.104}}} \right],{t_0} < t \end{array} \right.。$ | (15) |
由故障率浴盆曲线的定义可知设备在整个寿命周期主要经历3个阶段,而在各时间区间之间存在一个转折点,即关键时间拐点。对于文中的两参数威布尔分段模型,t0就是其分段函数的分界点及关键时间拐点。由于其可靠度函数与概率密度函数在其分界点处连续,则
| $ R\left( {t_0^ - } \right) = R\left( {t_0^ + } \right),f\left( {t_0^ - } \right) = f\left( {t_0^ + } \right)。$ | (16) |
因此由式(7)、(16) 可得
| $ {k_1}\exp \left[ { - {{\left( {{t_0}/{\alpha _1}} \right)}^{{\beta _1}}}} \right] = {k_2}\exp \left[ { - {{\left( {{t_0}/{\alpha _2}} \right)}^{{\beta _2}}}} \right]。$ | (17) |
| $ \begin{array}{*{20}{c}} { - \frac{{{k_1}{\beta _1}}}{{{\alpha _1}}}{{\left( {{t_0}/{\alpha _1}} \right)}^{{\beta _1} - 1}}\exp \left[ { - {{\left( {{t_0}/{\alpha _1}} \right)}^{{\beta _1}}}} \right] = }\\ { - \frac{{{k_2}{\beta _2}}}{{{\alpha _2}}}{{\left( {{t_0}/{\alpha _2}} \right)}^{{\beta _2} - 1}}\exp \left[ { - {{\left( {{t_0}/{\alpha _2}} \right)}^{{\beta _2}}}} \right]。} \end{array} $ | (18) |
令k1=1,由式(17) 与式(18) 可得
| $ {t_0} = {\left[ {{\beta _1}{\alpha _2}^{{\beta _2}}/{\beta _2}/{\alpha _1}^{{\beta _1}}} \right]^{1/\left( {{\beta _2} - {\beta _1}} \right)}}; $ | (19) |
| $ {k_2} = \exp \left[ {\left( {1 - {\beta _2}/{\beta _1}} \right){{\left( {{t_0}/{\alpha _2}} \right)}^{{\beta _2}}}} \right]; $ | (20) |
将式(14) 代入式(17) 和式(18) 可得
| $ {t_0} = 1441,{k_2} = 0.689。$ | (21) |
由式(15)、(21) 可得两参数威布尔分段模型的可靠度函数为
| $ \begin{array}{*{20}{c}} {R\left( t \right) = \left\{ \begin{array}{l} {k_1}\exp \left[ { - {{\left( {t/{\alpha _1}} \right)}^{{\beta _1}}}} \right]\\ {k_2}\exp \left[ { - {{\left( {t/{\alpha _2}} \right)}^{{\beta _2}}}} \right] \end{array} \right. = }\\ {\left\{ \begin{array}{l} \exp \left[ { - {{\left( {t/331} \right)}^{0.894}}} \right],0 < t \le 1412.67,\\ 0.6485\exp \left[ { - {{\left( {t/445} \right)}^{1.014}}} \right],1412.67 < t。\end{array} \right.} \end{array} $ | (22) |
因此,可以求得两参数威布尔分段模型的失效率函数为
| $ \begin{array}{*{20}{c}} {\lambda \left( t \right) = - \frac{{\rm{d}}}{{{\rm{d}}t}}\ln R\left( t \right) = \left\{ \begin{array}{l} \frac{{{\beta _1}}}{{{\alpha _1}}}{\left( {t/{\alpha _1}} \right)^{{\beta _1} - 1}}\\ \frac{{{\beta _2}}}{{{\alpha _2}}}{\left( {t/{\alpha _2}} \right)^{{\beta _2} - 1}} \end{array} \right. = }\\ {\left\{ \begin{array}{l} 0.0027{\left( {t/331} \right)^{ - 0.106}}, - 0 < t \le 1412.67,\\ 0.00228{\left( {t/445} \right)^{0.014}}, - 1412.67 < t, \end{array} \right.} \end{array} $ | (23) |
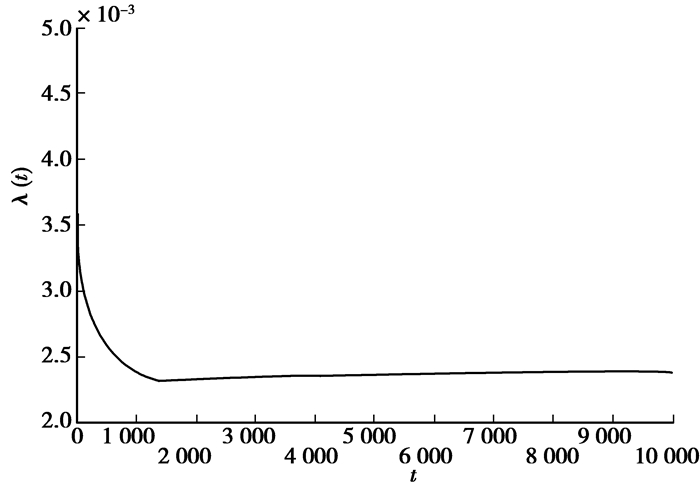
其图形如图 3所示。
|
图 3 两重威布尔分段分布模型故障率函数图 |
由计算结果可得,该系列卧式加工中心的早期故障期约有1 412 h,按平均每天工作14 h计算,则该系列卧式加工中心早期故障期将持续3个月之久。这与用户反映的加工中心故障频繁时间相差不大,因此可以表明,该模型正确,数据可信。
2 机床最佳保修期研究保修是指产品(或元件、系统)的生产者与经销商根据保修条款为确保产品在正常使用的情况下,一定时期内性能充分满足所规定的要求而做出的一种承诺,要求生产者与经销商在一定时期,在规定的条件下,必须对产品出现的故障向顾客进行补偿[13]。文献[14]分别从用户和企业的角度,阐述了确定最佳保修期对双方的利益。由于产品的保修期主要是针对其早期失效,因此,可以断定该系列加工中心的保修期应在偶然故障期之内。
在确定该系列加工中心最佳保修期之前,作如下假设:
假设一:该系列加工中心发生故障后,采取的维修方式为最小维修,这种维修只是更换或修复那些直接导致设备失效的元件,而不对其它元件进行维修或更换。在这种维修方式下,并不改变设备的失效函数,只使设备从失效状态恢复到工作状态[15]。因此,在时间区间(0,T]内的平均维修次数为
| $ M\left( t \right) = \int_0^T {\lambda \left( t \right){\rm{d}}t} 。$ | (24) |
假设二:由于设备进入耗损故障期后,其维修费用增大,所创造的效益相对减少,因此忽略设备在耗损故障期内的效益,即设备的使用寿命截至其偶然故障期。
在上述两条假设的前提下,企业生产销售一台加工中心的经济效益为
| $ {E_1} = \frac{P}{{{C_0} + {C_r}\left[ {\int_0^{{t_0}} {\lambda \left( t \right)dt} + \int_0^T {\lambda \left( t \right){\rm{d}}t} } \right]}}, $ | (25) |
式中:P为该加工中心平均每台的售价,P=3 500 000;
C0为制造该加工中心的平均每台成本,C0=1 800 000;
Cr为每次故障的平均修复费用,Cr=5 000;
T为该系列加工中心的最佳保修期;
用户购买使用该加工中心的经济效益为
| $ {E_2} = \frac{{b\left( {L - N{t_r}} \right)}}{{{C_1} + {C_2} + {C_3} + P}}, $ | (26) |
式中:b为加工中心在使用过程中单位时间创造的收益,b=500;
L为加工中心的寿命,L=72 000;
tr为该系列加工中心每次故障的平均修复时间,tr=100;
N为该系列加工中心在寿命周期内的故障次数,
C1为该系列加工中心因发生故障造成的损失,C1=NtrCL;
CL为该系列加工中心在单位故障时间的损失费用,CL=50;
C2为该系列加工中心在寿命周期内的使用费用,C2=Cu(L-Ntr);
Cu为该系列加工中心单位时间的使用费用,Cu=20;
C3为用户在保修期后所支付的维修费用
由式(25)、(26) 可以看出,在其他因素不变的情况下,保修期越长,企业的经济效益下降,而用户的经济效益上升;保修期越短,则企业的经济效益上升,用户的经济效益下降。保修期的过长或过短都必将损害一方的利益[16]。因此,采用企业效益与用户效益同时相对最大来确定该系列加工中心最佳保修期。
目标函数为
| $ {\rm{Max}}{E_1} = \frac{P}{{{C_0} + {C_r}\left[ {\int_0^{{t_0}} {\lambda \left( t \right)dt} + \int_0^T {\lambda \left( t \right){\rm{d}}t} } \right]}}, $ | (27) |
| $ {\rm{Max}}{E_2} = \frac{{b\left( {L - N{t_r}} \right)}}{{{C_1} + {C_2} + {C_3} + P}}, $ | (28) |
约束条件为
E1>1,E2>1,T>0,T < L。
通过MATLAB运算求得最佳保修期11 077 h,按每天工作14 h计算,保修时间为791天。此时企业和用户利益同时相对达到最大。
3 结论在加工中心的故障时间数据的基础上,分析了其早期故障期和偶然故障期的故障分布规律。基于全寿命周期的观点,建立包含早期故障期、偶然故障期的加工中心故障率分布曲线,并运用高等数学方法确定了其关键时间拐点。得出某机床厂的某系列加工中心早期故障期和偶然故障期的分界点大约为1 000 h,与用户反映的时间相差不大。并利用该系列加工中心故障率分布曲线作为理论模型用来确定其最佳保修期,对企业效益和用户效益进行平衡优化,使企业与用户同时获得最大的效益。同时,该方法可以应用于其他复杂机电设备,具有良好的工程应用前景。
| [1] | Lai C D, Xie M. M.Bathtub-Shaped Failure Rate Life Distributions[M]//N.Balakrishnan, C.R.Rao, Handbook of Statistics. Netherlands:Elsevier Science B.V., 2001:69-104. https://link.springer.com/chapter/10.1007/978-3-642-39106-4_1 |
| [2] | Rodrigo B. G M. A new distribution with decreasing, increasing and upside-down bathtub failure rate[J]. Computational Statistics and Data Analysis, 2010, 54(4): 935–944. DOI:10.1016/j.csda.2009.10.006 |
| [3] | Xie M, Tang Y, Goh T N. A modified Weibull extension with bathtub-shaped failure rate function[J]. Reliability Engineering and System Safety, 2002, 76(3): 279–285. DOI:10.1016/S0951-8320(02)00022-4 |
| [4] |
李瑞莹, 康锐.
基于ARMA模型的故障率预测方法研究[J]. 系统工程与电子技术, 2008, 30(8): 1588–1591.
LI Ruiying, KANG Rui. Research on failure rate forecasting method based on ARMA model[J]. Systems Engineering and Electronic, 2008, 30(8): 1588–1591. (in Chinese) |
| [5] | Jones J A, Hayes J A. Use of a field failure database for improvement of product reliability[J]. Reliability Engineering & System Safety, 1997, 55(2): 131–134. |
| [6] | Yu J, Jia Y Z. Applied research on reliable increase measures of CNC lathes[J]. Journal of Harbin Institute of Technology (New Series), 2005, 12(2): 218–220. |
| [7] | 廖小波. 机床故障率浴盆曲线定量化建模及应用研究[D]. 重庆: 重庆大学, 2010. http://www.oalib.com/paper/4249750 |
| [8] |
赵继俊, 邹经湘, 张锡清.
混合威布尔分布的参数优化估计[J]. 机械科学与技术, 2001, 20(1): 14–16.
ZHAO Jijun, ZOU Jingxiang, ZHANG Xiqing. Parameter optimization estimation of mixed weibull distribution[J]. mechnical science and technology, 2001, 20(1): 14–16. (in Chinese) |
| [9] |
贾志成, 申桂香, 胡仲翔, 等.
基于生命周期的数控车床寿命分布模型及控制[J]. 机床与液压, 2008, 36(1): 164–168.
JIA Zhicheng, SHEN Guixiang, HU Zhongxiang, et al. Lifetime distribution model and control for CNC lathes based on life cycle[J]. machine tool & hydraulics, 2008, 36(1): 164–168. (in Chinese) |
| [10] | 蒋仁言, 左明健. 可靠性模型与应用[M]. 北京: 机械工业出版社, 1999. |
| [11] | Govind S.Mudholkar, Kobby O. Transformation of the bathtub failure rate data in reliability for using Weibull-model analysis[J]. Statistical Methodology, 2009, 6(6): 622–633. DOI:10.1016/j.stamet.2009.07.003 |
| [12] | 贺国芳. 可靠性数据的收集与分析[M]. 北京: 国防工业出版社, 1995. |
| [13] | Blischke W R, Murthy DNP. Product warranty handbook[M]. New Yourk: Marcel Dekker, 1996. |
| [14] | 解晶. 保修策略下的成本与保修期研究[D]. 天津: 天津大学, 2005. |
| [15] | Wu C C, Chou C Y, Chikong H. Optimal burn-in time and warranty length under fully renewing combination free replacement and pro-rata warranty[J]. Reliability Engineering & System Safety, 2007, 92(7): 914–920. |
| [16] |
胡飞, 宗群.
基于产品保修的不可靠生产系统最优生产周期[J]. 系统工程与电子技术, 2009, 31(1): 479–483.
HU Fei, ZONG Qun. Optimal production run length for an unreliable production system based on product warranty policy[J]. Systems Engineering and Electronic, 2009, 31(1): 479–483. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

