2. 西安科技大学 通信与信息工程学院, 西安 710054
2. College of Communication and Information of Engineering, Xi'an University of Science and Technology, Xi'an 710054, China
超宽带(UWB)以其高速率、大容量、低功耗、低成本、精确定位等优良特性在短距离无线通信中有着广泛的应用前景[1-2]。然而,在室内环境中,UWB无线信道具有密集多径的特点,由此引起的码间干扰(ISI)会严重地影响系统性能。此外,随着系统用户数的增加,多址干扰(MAI)也成为影响UWB系统性能的重要因素。因此,设计适合于实际应用的高性能、低复杂度的接收机也是UWB的重要研究方向。
传统的Rake接收机[3]能有效合并多径信号,从而获得分集增益,提高系统性能。但是,在典型的室内环境中,UWB信道响应的时延扩展长达80~200 ns,路径数多达几十乃至上百条,随着Rake接收机支路(finger)数的增加,其实现复杂度将难以接受[4-5],且Rake接收机在MAI情况下性能受限。为了有效抑制MAI,多用户检测技术(MUD)技术也被应用于UWB系统中,考虑到所需较少先验知识等因素,一些盲MUD方案更被关注[6],其中最重要的是盲最小均方误差(MMSE)检测器,其批处理实现主要包括直接法(DMI)和子空间法(SS)[7],但因涉及到矩阵求逆或特征值分解(ED)等问题,这两种方法计算量均很大,且不能满足实时性要求。进一步考虑到无线信道的动态特性,盲自适应MUD方案便成为解决在线实现问题的关键,与两种批处理方法对应的常用自适应算法分别是最小输出能量(MOE)[8]和紧缩近似投影子空间跟踪(PASTd)[9]。然而,随着检测数据维数的增加,自适应滤波器的长度也相应的增加,这导致了计算复杂度的增加及滤波器稳健性的下降。为了减小算法复杂度,降维自适应滤波技术也受到人们的青睐,包括:主分量法(PC)、互谱法(CS)和多级维纳滤波器(MSWF)[10]。其中PC法和CS法均需要通过特征值分解得到降维子空间,运算量较大,相比较而言,MSWF无需特征值分解,具有较低的计算复杂度和接近于满秩MMSE接收机的性能。
笔者提出一种适用于UWB系统的盲自适应降秩多用户检测方案,该方案分为两步实现:第一步将MOE算法和MSWF方法相结合,实现盲自适应解相关;第二步采用PASTd方法进行信道估计并进行最大比合并(MRC),进一步提高输出信干噪比(SINR)。该方案具有计算复杂度低、所需先验知识较少等优点,仿真结果表明,其能有效抑制ISI和MAI,且收敛较快。
1 系统模型考虑一个含有K个用户的直扩超宽带(DS-UWB)系统,第k个用户的发射信号可表示为[11]
| $ {x_k}\left( t \right) = \sum\limits_{m = 0}^{M - 1} {{b_k}\left( m \right)} \sum\limits_{n = 0}^{N - 1} {{c_k}\left( n \right)w\left( {t - mT - n{T_c}} \right)} , $ | (1) |
其中,bk(m)∈{±1}和ck(n)∈{±1}分别是第k个用户发送的周期为T的信息比特和扩频增益为N的扩频序列,w(t)是周期为Tc=T/N且具有单位能量的UWB脉冲波形,其设计需满足FCC关于UWB信号的频谱限制。
xk(t)通过的UWB多径信道设为hk(t),其通常采用IEEE802·15·3a的室内信道模型[12-13],该模型是修正的S-V模型,特点是多径分量以簇的形式到达,hk(t)可建模为
| $ {h_k}\left( t \right) = {G_k}\sum\limits_{p = 1}^{{L_c}} {\sum\limits_{q = 1}^{L\left( p \right)} {{\alpha _{k,p,q}}\delta \left( {t - {T_{k,p}} - {\tau _{k,p,q}}} \right)} } 。$ | (2) |
式中Gk是第k个用户的幅度增益,Lc是观测到的簇的数目,L(p)是第p簇内接收到的多径数目,Tk, p是用户k的第p簇的到达时间,αk, p, q和τk, p, q分别是用户k的第p簇中第q条路径的系数和时延。
K个用户信号通过UWB信道后,上行链路总的接收信号可表示为
| $ y\left( t \right) = \sum\limits_{k = 1}^K {{x_k}\left( t \right) * {h_k}\left( t \right)} + v\left( t \right), $ | (3) |
式中:*表示卷积运算;v(t)是均值和方差分别为0和σ2的加性高斯白噪声(AWGN)。为了简化分析,假定信道中可分辨路径的最小时间间隔(时间仓)等于Tc,且K个用户信道中最大路径数为L+1,则y(t)经过码片匹配滤波器并以1/Tc速率采样后,第i个样值为
| $ \begin{array}{*{20}{c}} {y\left( i \right) = \int_{i{T_c}}^{\left( {i + 1} \right){T_c}} {y\left( t \right)w\left( {t - i{T_c}} \right)} = }\\ {\sum\limits_{k = 1}^K {\sum\limits_{m = 0}^{M - 1} {{b_k}\left( m \right)\sum\limits_{l = 0}^L {{h_k}\left( l \right){c_k}\left( {i - mN - l} \right)} } } + v\left( i \right),} \end{array} $ | (4) |
式中,
假设用户1为期望用户,且L < N,同时定义向量y(m)=[y(mN), …, y(mN+N+L-1)]T,则离散接收信号模型可表示为
| $ \mathit{\boldsymbol{y}}\left( m \right) = {\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{h}}_1}{b_1}\left( m \right) + \mathit{\boldsymbol{u}}\left( m \right), $ | (5) |
式中,C1为用户1各路径的拓展特征波形向量,可定义为第1行和第1列分别是[c1(0), 0, …, 0]和[c1(0), …, c1(N-1), 0, …, 0]T的(N+L)×(L+1) 维Toeplitz矩阵;h1=[h1(0), …, h1(L)]T为信道系数向量;b1(m)为期望检测的符号;而u(m)为一包含有ISI、MAI及AWGN的向量。
2 盲自适应降秩接收机笔者提出的盲自适应降秩接收机可分两步实现,首先将MOE算法和MSWF方法相结合,来抑制MAI,提取期望用户多径分量;再通过PASTd估计信道从而对分离出的多径分量进行最大比合并。MOE可实现盲自适应解相关,结合MSWF可减少滤波器的维数,降低复杂度;而PASTd算法可以自适应精确估计信道,提高输出SINR。其原理如图 1所示。
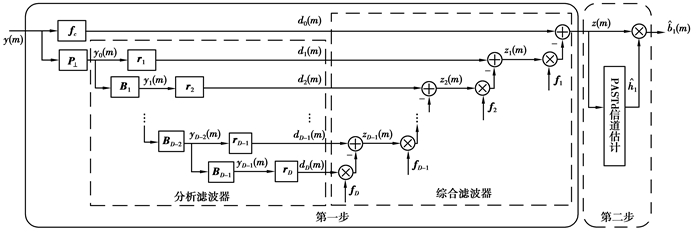
|
图 1 盲自适应降秩接收机结构 |
设期望用户1的滤波器系数f为一个(N+L)×(L+1) 维矩阵,则该滤波器基于MOE算法的约束代价函数可定义为
| $ \begin{array}{*{20}{c}} {\mathop {\min J}\limits_f = E\left\{ {{{\left\| {{\mathit{\boldsymbol{f}}^{\rm{H}}}\mathit{\boldsymbol{y}}\left( m \right)} \right\|}^2}} \right\},}\\ {{\rm{s}}.{\rm{t}}.\;\mathit{\boldsymbol{C}}_1^{\rm{H}}\mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{I}}_{\left( {L + 1} \right)}},} \end{array} $ | (6) |
式中I(L+1)表示(L+1)×(L+1) 维单位矩阵,为了便于求解,采用广义旁瓣相消器(GSC)可将式(6) 转化为无约束优化问题。分别定义C1上的投影矩阵P=C1(C1HC1)-1C1H和正交投影矩阵P⊥=I(N+L)-P,将f分解成相互正交的2部分
| $ \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{f}}_c} - {\mathit{\boldsymbol{P}}_ \bot }{\mathit{\boldsymbol{f}}_a}, $ | (7) |
其中fc=Pf=C1(C1HC1)-1为固定部分。fa为(N+L)×(L+1) 维矩阵,将式(7) 代入式(6) 得
| $ \begin{array}{*{20}{c}} {\mathop {\min J}\limits_{{f_a}} = E\left\{ {{{\left\| {{\mathit{\boldsymbol{d}}_0}\left( m \right) - \mathit{\boldsymbol{f}}_a^{\rm{H}}{\mathit{\boldsymbol{y}}_0}\left( m \right)} \right\|}^2}} \right\} = }\\ {{\rm{tr}}\left( {{\mathit{\boldsymbol{I}}_{\left( {L + 1} \right)}}} \right) + {\rm{tr}}\left( {\mathit{\boldsymbol{f}}_a^{\rm{H}}{\mathit{\boldsymbol{R}}_{{y_0}}}{\mathit{\boldsymbol{f}}_a}} \right) - 2{\rm{tr}}\left( {\mathit{\boldsymbol{f}}_a^{\rm{H}}{\mathit{\boldsymbol{R}}_{{y_0}{d_0}}}} \right),} \end{array} $ | (8) |
式中,y0(m)=P⊥Hy(m)为(N+L)×1维向量,d0(m) =(C1HC1)-1C1Hy(m)为(L+1)×1维列向量,而Ry0=E{y0(m)y0H(m)}为前者的自相关矩阵,ry0d0=E{y0(m)d0H(m)}为二者的互相关矩阵,tr(·)表示迹运算。式(8) 的最优解为
| $ {\mathit{\boldsymbol{f}}_a} = \mathit{\boldsymbol{R}}_{{\mathit{\boldsymbol{y}}_0}}^{ - 1}{r_{{\mathit{\boldsymbol{y}}_0}{d_0}}}。$ | (9) |
上式为一标准维纳滤波器,随着输入数据向量维数的增大,其相应的矩阵运算就会越复杂,而MSWF通过逐级对输入信号作正交投影分解,将标准的维纳滤波器的求解过程分解为一个嵌套链式结构,降低了维数,减小了计算复杂度,其结构如图 1中第一部分所示,从功能上,MSWF可分为分析滤波器和综合滤波器两部分:分析滤波器在每一级上对输入信号作正交投影分解,通过多级分解减小了数据向量的维数;而综合滤波器将分析滤波器的输出作为操作对象,采用MMSE准则。与传统MSWF[10]不同的是:di(m)是一个维数为L+1的向量,且每一级可减少L+1维[14-15],滤波器的最大级数为
| 表 1 MSWF-MOE算法 |
通过第一步MSWF-MOE滤波后,可抑制输入数据向量中的大部分MAI和ISI,其输出z(m)为(L+1)×1维列向量,主要包含了期望用户的待检测的各多径分量,可表示为
| $ z\left( m \right) = {\mathit{\boldsymbol{f}}^{\rm{H}}}\mathit{\boldsymbol{y}}\left( m \right) = {\mathit{\boldsymbol{h}}_1}{b_1}\left( m \right) + \mathit{\boldsymbol{e}}\left( m \right), $ | (10) |
式中e(m)=fHu(m)为滤波器对干扰和噪声部分的输出。为了进一步提高输出SINR,可对z(m)中的各分量进行最大比合并,理论上,最佳合并向量[16]为Rzz-1h1,其中h1需通过信道估计求得。但由于z(m)中期望用户1的信号功率远大于e(m)中各分量的功率,即有
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{zz}} = E\left\{ {z\left( m \right)z{{\left( m \right)}^{\rm{H}}}} \right\} = }\\ {{\mathit{\boldsymbol{h}}_1}\mathit{\boldsymbol{h}}_1^{\rm{H}} + E\left\{ {\mathit{\boldsymbol{e}}\left( m \right)\mathit{\boldsymbol{e}}{{\left( m \right)}^{\rm{H}}}} \right\} \approx {\mathit{\boldsymbol{h}}_1}\mathit{\boldsymbol{h}}_1^{\rm{H}}。} \end{array} $ | (11) |
因此,使用最大比合并估计信道系数向量h1,即
| $ \mathop {{\mathit{\boldsymbol{h}}_1}}\limits^ \wedge = \mathop {\arg \max }\limits_{\left\| {{h_1}} \right\| = 1} \mathit{\boldsymbol{h}}_1^{\rm{H}}{\mathit{\boldsymbol{R}}_{zz}}{\mathit{\boldsymbol{h}}_1}, $ | (12) |
式中
| $ J\left( {\mathop {{\mathit{\boldsymbol{h}}_1}}\limits^ \wedge \left( j \right)} \right) = {\sum\limits_{m = 0}^j {{\beta ^{j - m}}\left\| {\mathit{\boldsymbol{z}}\left( m \right) - \mathop {{\mathit{\boldsymbol{h}}_1}}\limits^ \wedge \left( j \right)\mathop {\mathit{\boldsymbol{h}}_1^{\rm{H}}}\limits^ \wedge \left( j \right)\mathit{\boldsymbol{z}}\left( m \right)} \right\|} ^2}, $ | (13) |
式中0<β≤1为遗忘因子,当m接近j时,
| $ g\left( m \right) = \mathop {\mathit{\boldsymbol{h}}_1^{\rm{H}}}\limits^ \wedge \left( {j - 1} \right)\mathit{\boldsymbol{z}}\left( m \right)。$ | (14) |
来近似代替
| $ \tilde J\left( {\mathop {{\mathit{\boldsymbol{h}}_1}}\limits^ \wedge \left( j \right)} \right) = {\sum\limits_{m = 0}^j {{\beta ^{j - m}}\left\| {\mathit{\boldsymbol{z}}\left( m \right) - \mathop {{\mathit{\boldsymbol{h}}_1}}\limits^ \wedge \left( j \right)g\left( m \right)} \right\|} ^2}。$ | (15) |
可采用RLS算法自适应更新
| 表 2 PASTd主特征值跟踪算法 |
最后,期望用户1的符号数据可以通过下式估计
| $ {{\overset{\wedge }{\mathop{\mathit{b}}}\,}_{1}}\left( \mathit{m} \right)=\rm{sign}\left\{ \mathit{Re}\left[ \overset{\wedge }{\mathop{\mathit{\boldsymbol{h}}_{1}^{\rm{H}}}}\,{{\mathit{\boldsymbol{f}}}^{\rm{H}}}\mathit{\boldsymbol{y}}\left( \mathit{m} \right) \right] \right\}, $ | (16) |
其中,sign(·)为符号函数,Re(·)表示复数的实部。
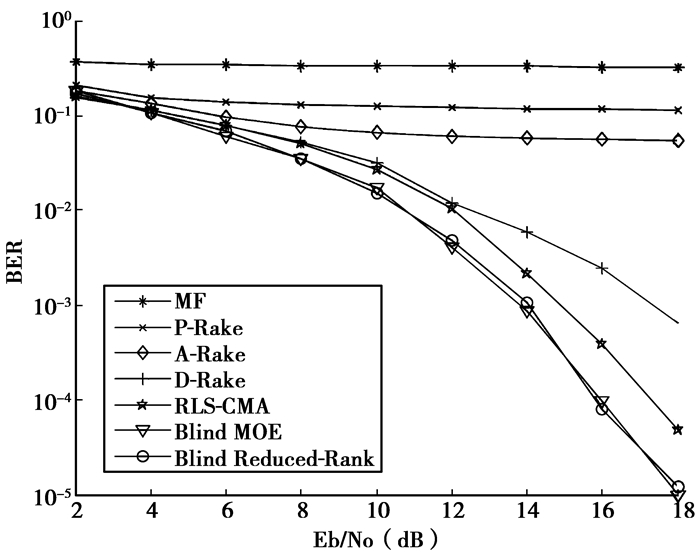
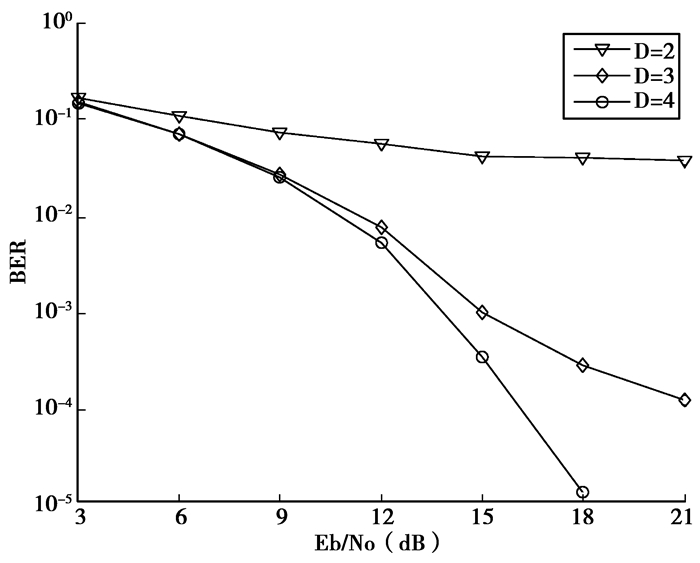
3 仿真及性能分析仿真实验考虑一个多径、多用户环境下的DS-UWB系统,扩频码采用扩频增益N=31的Gold序列,UWB脉冲波形为二阶导高斯脉冲,信道采用IEEE802·15·3a CM1的室内信道模型。图 2为用户数K=16条件下,几种接收机误码率随Eb/N0变化情况的比较,其中匹配滤波器(MF)是UWB系统中最简单、最常用的接收机之一,但其仅在加性高斯白噪声(AWGN)信道下具有最佳性能,仿真结果表明,在多径、多用户环境下,匹配滤波器(MF)既不能消除多径干扰也不能抑制多址干扰,所以完全失效。传统Rake接收机能有效收集多径能量,但在多用户环境下,Rake接收机性能受限,仿真结果也显示,当用户数K=16时,随着Eb/N0的增加,支路数为6的部分Rake接收机(P-Rake)[3]以及全Rake接收机(A-Rake)[3]误码性能均不理想,主要因为传统Rake接收机不能消除多址干扰。采用约束代价函数的解相关Rake接收机(D-Rake)[16]是传统Rake接收机的改进方案,能有效抑制多址干扰,且能合并最先到达的6条路径,性能优于前3种接收机,但其性能的提高依赖于接收机支路数的增加,这会导致复杂度的相应增加。基于约束恒模算法(CMA)的盲自适应接收机(RLS-CMA)[17]需要较少的先验知识且具有较低的复杂度,从仿真图可以看出,在高Eb/N0时,该接收机性能改善明显,优于D-Rake接收机,但其性能依赖于RLS算法中遗忘因子选择。而所提出的盲自适应降秩接收机(blind reduced-rank)在降低计算复杂度的同时,可获得与文献[8]中的盲最小输出能量接收机(blind MOE)相同的性能。图 3为用户数K=16条件下,盲自适应降秩接收机的第一步中MSWF取不同级数(D)时,误码率性能比较,当存在10条(L=9) 可分辨路径时,MSWF每经过一级迭代输出向量维数会减少10,由图可知,随着级数的增加误码率相应的减小,但最大级数需满足条件
|
图 2 K=16时几种接收机误码性能比较 |
|
图 3 盲降秩接收机中MSWF取不同级数时误码性比 |
|
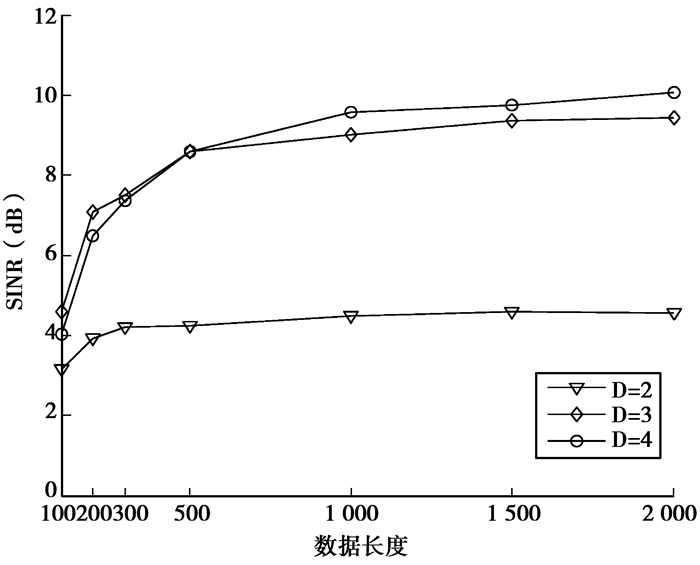
图 4 不同级数下数据长度对输出信干噪比的影响 |
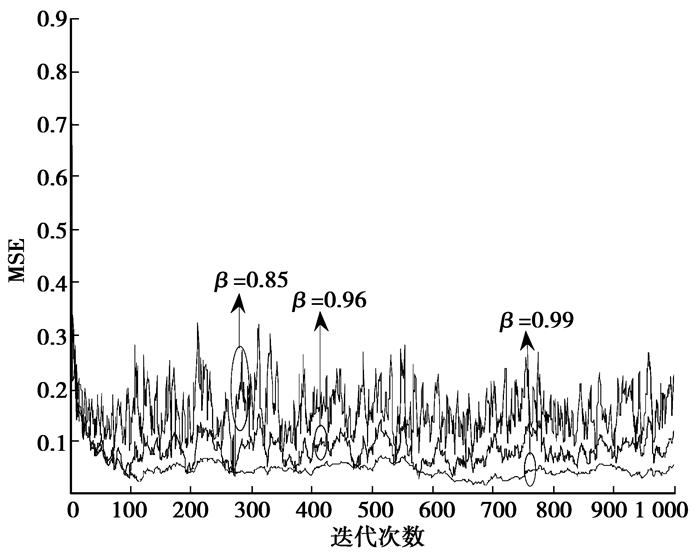
|
图 5 遗忘因子β取不同值时PASTd收敛情况比较 |
多址干扰和码间干扰是影响UWB系统性能的主要因素,提出一种盲自适应降秩接收机,该接收机通过两步来抑制系统中的多址干扰及码间干扰。仿真结果表明,在多径信道、多用户环境下,其性能优于传统的Rake接收机、解相关Rake接收机和基于恒模算法的自适应接收机,且具有所需先验知识较少、计算复杂度较低、收敛较快等优点,适用于室内UWB的多用户高速接人场合。
| [1] | Zhuo Z, Mendoza D S, WANG P, et al. A low-power and flexible energy detection IR-UWB receiver for RFID and wireless sensor networks[J]. IEEE Trans. on Circuits and Systems, 2011, 58(7): 1470–1482. DOI:10.1109/TCSI.2011.2142930 |
| [2] | Liu K H, Shen X M, Zhang R N, et al. Performance Analysis of Distributed Reservation Protocol for UWB-based WPAN[J]. IEEE Trans. on Vehicular Technology, 2009, 58(2): 902–913. DOI:10.1109/TVT.2008.928638 |
| [3] | Cassioli D, Win M Z, Vatalaro F, et al. Low complexity Rake receivers in ultra wideband channels[J]. IEEE Trans. on Wireless Commun, 2007, 6(4): 1265–1275. DOI:10.1109/TWC.2007.348323 |
| [4] | Malik W Q, Stevens C J, Edwards D J. Multipath effects in ultra wideband Rake reception[J]. IEEE Trans. on Antennas and Propagation, 2008, 56(2): 507–514. DOI:10.1109/TAP.2007.915414 |
| [5] | Mohsenian A H, Mietzner J, Schober R, et al. Pre-equalization for pre-rake DS-UWB systems with spectral mask constraints[J]. IEEE Transa on Commun ication, 2011, 59(3): 780–791. DOI:10.1109/TCOMM.2011.122110.090718 |
| [6] | Zhang D, Wang K, Zhang X. Blind adaptive affine projection algorithm-based multi-user detector over a multi-path fading channel[J]. Signal Processing, 2010, 90(6): 2102–2106. DOI:10.1016/j.sigpro.2009.12.007 |
| [7] | Cheng C H, Lin W J, Chen K J. Subspace-based blind multi-user detection for TH-UWB systems in multi-path channels[J]. WSEAS Transaction on Communications, 2008, 7(8): 796–806. |
| [8] | Xu Z Y, Liu P, Wang X D. Blind multiuser detection:from MOE to subspace methods[J]. IEEE Trans. on Signal Processing, 2006, 25(2): 510–524. |
| [9] | Yang B. Projection approximation subspace tracking[J]. IEEE Trans on Signal Processing, 1995, 43(1): 95–107. DOI:10.1109/78.365290 |
| [10] | Goldstein J S, REED I S, SCHARF L L. A multistage representation of the wiener filter based on orthogonal projections[J]. IEEE Trans. on Signal Processing, 1998, 44(7): 2943–2959. |
| [11] | Ahmed Q Z, Yang L L, Chen S. Reduced rank adaptive least bit-error-rate detection in hybrid direct sequence time-hopping ultrawide bandwidth systems[J]. IEEE Trans. on Vehicular Technology, 2011, 60(3): 849–857. DOI:10.1109/TVT.2011.2109974 |
| [12] | Hao K, Gubner J A. The distribution of sums of path gains in the IEEE 802.15.3a UWB channel model[J]. IEEE Trans. on Wireless Commun, 2007, 6(3): 811–816. DOI:10.1109/TWC.2007.05438 |
| [13] | Molisch A F. Ultra-wide-band propagation channels[J]. Proceedings of the IEEE, 2009, 97(2): 353–371. DOI:10.1109/JPROC.2008.2008836 |
| [14] | Hu C C, Lin H Y. Multiuser detection using adaptive multistage matrix wiener filtering schemes with stage selection criteria in DS-UWB[J]. EURASIP journal on Advances in Signal Processing, 2008, 1: 1–9. |
| [15] |
谢跃雷, 欧阳缮, 赖伟明.
多径衰落信道下的一种盲多用户检测方法[J]. 通信学报, 2005, 26(2): 51–55.
XIE Yuelei, OUYANG Shan, LAI Weiming. Blind multi-user detection approach to multi-path fading channel[J]. Journal on Communications, 2005, 26(2): 51–55. (in Chinese) |
| [16] | Liu H, Li K. A decorrelating RAKE receiver for CDMA communications over frequency selective fading channels[J]. IEEE Trans. Commun, 1999, 47(7): 1036–1045. DOI:10.1109/26.774854 |
| [17] | Kang X, Yang J, MEN S. Blind adaptive receiver based on RLS-CMA for TH-UWB system[J]. The Journal of China Universities of Posts and Telecommunications, 2011, 18(6): 38–43. DOI:10.1016/S1005-8885(10)60120-3 |
 2013, Vol. 36
2013, Vol. 36

