2. 西安石油大学 电子工程学院, 陕西西安, 710065
2. College of Electronic Engineering, Xi'an Shiyou University, Xi'an 710065, China
目前,中国油田上采用的主要采油设备仍然是抽油机,其保有量在10×104台以上,电动机装机总容量在3 500 MW,每年耗电量逾100×108度。抽油机的运行效率特别低[1],在中国平均效率为25.96%,而国外平均水平为30.05%,年节能潜力可达几十亿度,因此对抽油机的节能增产研究显得尤为重要。
近年来,已有不少学者研究抽油机节能策略,并取得了一些前瞻性的成就,主要分为以下两类:一类是引入新的机械或电气设备,另一类是则是采用新的工作方式[2]。第一类方法主要是通过变换装备,改变抽油机或电动机的一些机械结构和特性,典型的有文献[3]通过对CYJY12-4.8-73HB型偏置抽油机支架进行改进,使得抽油机的设计更合理,实现节能目的。文献[4]提出了一种ZXCY型直线电动机抽油机用于油田的采油,这种抽油机能使能量转化率提高23%。文献[5]采用了一种单速三功率档节能型电机,这能使额定转速、效率、功率因素等相近,从而达到节能目的。文献[6]尝试用连续量子粒子群优化抽油机的结构参数,设计节能型抽油机。这些方法虽然能够明显的提高抽油机的系统效率,但是随着油田的不断开采,油田的内在环境不断的变化,机械节能改进结构的方法不能适应系统的变化,同时,需要改变抽油机的结构或更新设备,这在一定程度上造成了对油田原有设备的破坏和浪费。第二类方法主要是采用间歇式运行方式[7-8],这种方式是用定时启动运行、定时停机来控制抽油机,例如,Li等[9],Qi等[10]分别引入模糊神经网络来控制抽油机抽停节奏,从而实现节能。然而,这种方式是以损失产量为代价的,且这种方式是自动启动运行,存在不安全因素,在油田一般不允许使用。鉴于上述方法存在的一些问题,希望找到一种方法既能保证安全生产又能在原有的设备基础上对抽油机采油系统进行优化。让抽油机的工艺参数工作在最理想状态是一种实现增产节能的重要方法。这种方法操作简单,不需要对改变硬件设备,只需要找出抽油机工作的最理想工艺参数。优化最理想工艺参数的关键是抽油机模型的建立。为此,笔者考虑建立抽油机采油系统整体的一个模型,通过这个模型用优化技术优化工艺,达到增产节能目的。
考虑到抽油机系统是一个复杂的非线性系统,用准确的数学模型通常很难描述它,而广义回归神经网络[11-13](ceneralized regression neural network,GRNN)具有很强的非线性映射能力,很高的容错性和很强的鲁棒性,适用于解决非线性系统建模问题。因此,采用GRNN来确定工艺参数与增产节能指标的映射关系,建立抽油机的多维映射模型;然后运用具有智能特性的基于Pareto的向量评价微粒群算法[14](vector evaluated particle swarm optimization based on Pareto,VEPSO-BP)对多维映射模型进行搜索,搜索增产节能最好的理想点,据此确定工艺参数的最优值;最后,根据优化后的工艺参数最优值进行实际生产指导。
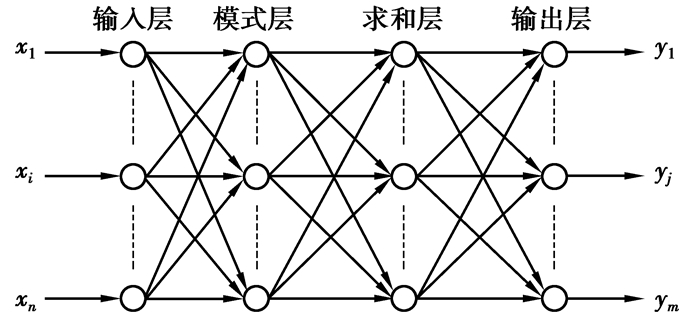
1 广义回归神经网络算法人工神经网络(ANN)因为其良好的非线性逼近能力和不需要知道系统内部具体结构仅通过系统输入输出数据就能模拟系统而被广泛应用于化工过程建模[15]。广义回归神经网络是一种具有很强的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性的神经网络。广义回归神经网络为4层类神经网络,分别为输入层,模式层,求和层,输出层,其模型架构见图 1。
|
图 1 广义回归神经网络架构 |
广义回归神经网络的理论基础是非线性回归分析,非独立变量Y相对于独立变量x的回归分析实际上是计算具有最大概率值的y。设随机变量x和随机变量y的联合概率密度函数为f(x, y),已知x的观测值为X,则y相对于X的回归,也即条件均值为
| $ \mathop Y\limits^ \wedge = E({y}{\rm{/}}{X}) = \frac{{\int_{ - \infty }^\infty {yf({X}, {y}){\rm{d}}{y}} }}{{\int_{ - \infty }^\infty {f({X}, {y}){\rm{d}}{y}} }}, $ | (1) |
对f(X, y)进行泊松(Parzen)非参数估计,由于
| $ \mathop Y\limits^ \wedge ({X}) = \frac{{\sum\limits_{i = 1}^n {{Y_i}{\rm{exp}}\left[-{\frac{{{{({X}{\rm{-}}{{X}_i})}^{\rm{T}}}({X}{\rm{-}}{{X}_i})}}{{2{\sigma ^2}}}} \right]} }}{{\sum\limits_{i = 1}^n {{\rm{exp}}\left[-{\frac{{{{({X}{\rm{-}}{{X}_i})}^{\rm{T}}}({X}{\rm{-}}{{X}_i})}}{{2{\sigma ^2}}}} \right]} }}, $ | (2) |
估计值
VEPSO-BP是一种多目标微粒群算法,其核心思想是将微粒群划分为若干个种群规模相等的子微粒群,分别对多个目标函数进行优化,并且各个子微粒群的适应值要受到其他子微粒群的影响。VEPSO-BP将p个种群规模都为M的子微粒群同时对多目标优化问题的p个目标函数进行优化,其中k(k=1, 2, …, p)个子微粒群k只负责优化第k个目标函数fk(U)。
相比VEPSO,VEPSO-BP在全局最优位置的赋值和更新上需要建立一个外部记忆体,并将所有p个子微粒群中的Pareto非支配解都放入该记忆体中,程序迭代式,需按照一定的算法从外部记忆体中取p个Pareto非支配解(可重复)分别作为各个子微粒群的全局最优位置。适用于VEPSO-BP的进化方程为
| $ \begin{array}{l} [{k}]{{v}_{{\rm{ad}}}}({\rm{gen}} + 1) = [{k}]{w + }{{v}_{{\rm{ad}}}}{\rm{(gen) + }}[{k}]{{c}_1} \times {r_1} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;[[{k}]{{p}_{{\rm{bes}}{{\rm{t}}_{{\rm{ad}}}}}} - [{k}]{x_{{\rm{ad}}}}{\rm{(gen)}}] + \\ \;\;\;\;\;[{k}]{{c}_2} \times {r_2} \times \;[[{k}]{{p}_{{\rm{bes}}{{\rm{t}}_{d}}}} - [{k}]{x_{{\rm{ad}}}}{\rm{(gen)}}], \end{array} $ | (3) |
| $ [{k}]{{v}_{{\rm{ad}}}}({\rm{gen}} + 1) = [{k}]{x_{{\rm{ad}}}}{\rm{(gen)}} + [{k}]{{v}_{{\rm{ad}}}}({\rm{gen}} + 1), $ | (4) |
其中:[k]xad(gen),[k]vad(gen),[k]pbestad,[k]gbestad分别为gen时刻,第k个子微粒群中,第a个微粒在第d维分量下的坐标、速度、局部最优位置和全局最优位置;[k]c1和[k]c2为微粒的加速因子;r1和r2为2个在[0, 1]范围内变化的随机数。
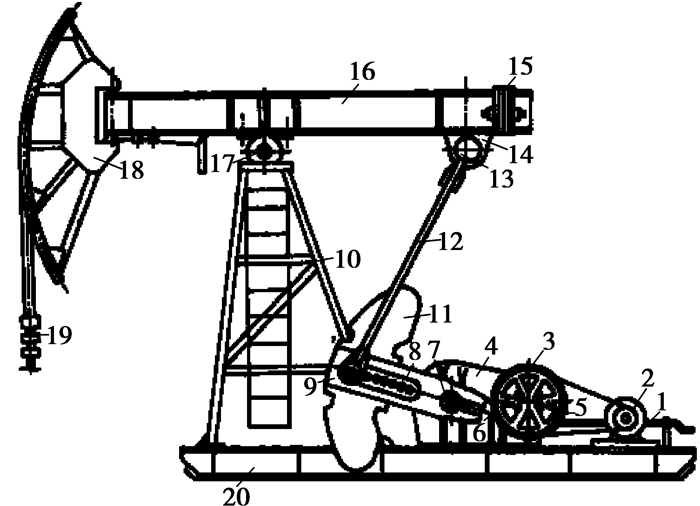
3 VEPSO-BP和GRNN的抽油机采油过程建模与决策参数优化 3.1 抽油机模型抽油机模型[16]如图 2所示,抽油机工作时,驴头悬点(图中19) 上作用的负载是变化的。抽油机工作分为上下两个冲程,抽油机上冲程时,驴头悬点需提起抽油杆柱和液柱,在抽油机未进行平衡的条件下,电动机(图中2) 要付出很大的能量,这时电动处于电动状态。在下冲程时,抽油机杆柱转拉动对电动机做功,使电动机处于发电机运行状态。
|
图 2 抽油机模型 |
抽油机工作过程中电能的消耗和油的产出量受很多过程变量的综合影响。这些过程变量与能耗和产油量呈非线性关系,传统建模方法很难得到精准的工艺能耗模型。GRNN具有很强的非线性映射能力,很高的容错性和很强鲁棒性,适用于解决非线性系统建模问题,能够对模型进行高精度拟合,为优化算法优化最优工艺提供了可行性和可靠性。
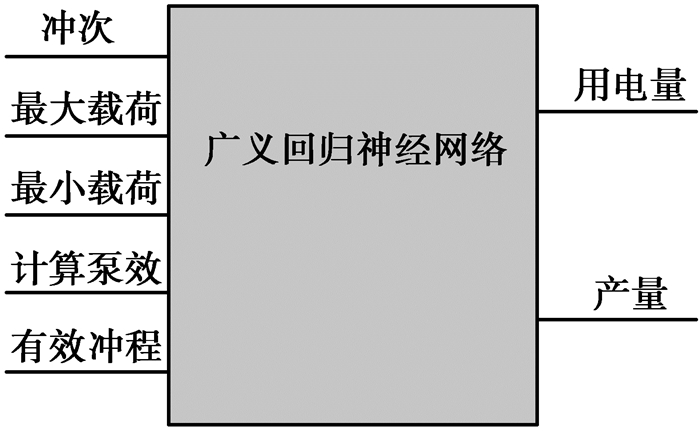
3.2 基于GRNN的抽油机生产系统建模抽油机采油系统中,冲次的大小与系统的生产状况是否合理是影响抽油机能耗和生产产量的关键因素,因此将冲次作为决策变量。考虑到冲次含有的信息量有限,仅用冲次对抽油机系统进行建模的效果很难接近真实模型,不足以反映真实的生产情况,为此,找出4个环境变量:最大载荷,最小载荷,有效冲程,计算泵效,结合冲次作为GRNN模型的输入变量,以用电量和产量作为输出,建立抽油机生产系统的模型,模型如图 3所示。
|
图 3 抽油机广义回归神经网络模型 |
在广义回归神经网络训练模型时,为了直观的表示测试样本的预测效果,采用均方差MSE和拟合优度U这2个指标来衡量,公式如下
| $ {\rm{MSE}} = \frac{{\sum {{{({{e}_i})}^2}} }}{N}, U = 1 - \frac{1}{N}\sum {\left| {\frac{{{e_i}}}{{{s_i}}}} \right|, } $ | (5) |
其中,si是期望值,ei是绝对误差,N是样本个数。
3.3 基于VEPSO-BP的抽油机采油过程决策参数优化GRNN建模得到了理想的抽油机采油模型后,需要再进行决策参数优化方能获得理想参数。考虑2个目标中用电量越小越好,产量越大越好,而VEPSO-BP算法是以目标最小为优化方向,为此,将产量转换为负数,与用电量结合,作为多目标优化的2个目标函数。即目标函数为
| $ \begin{array}{l} {\rm{object1Min}}\;{{\rm{G}}_{EPC}}({{X}_i}), {i = }{\rm{1, 2, }} \cdot \cdot \cdot {\rm{, 5;}}\\ {\rm{object2Min}}\;{{\rm{G}}_{OY}}({{X}_i}), {i = }{\rm{1, 2, }} \cdot \cdot \cdot {\rm{, 5;}} \end{array} $ | (6) |
其中,GEPC(Xi)为用电量的目标函数,GOY(Xi)为产量的目标函数,i=1, 2, …, 5为对应的5个参数。
由于研究的目的是寻找抽油机采油系统的最优决策参数,达到节能增产的目的,而环境变量在特定的状态下变化不大,为此把环境变量的搜索范围设置得较小,表示在特定的环境下,环境的变化不大。
4 实验及结果分析为了验证提出方法的合理性和有效性,在真实的油田数据上进行了大量实验。
4.1 数据选取与预处理笔者采用xx油田G17号和B24号2口井2011年6月1号到2011年10月18号的生产数据。经过人工处理粗大误差后分别得到1 521组数据和1 539组数据,为了对比结果,最后都采用前1 520组数据来进行试验,部分生产数据如表 1所示。方便起见,表格中用符号No.、P、Lmax、Lmin、S、E、C、Y分别表示序号、冲次、最大载荷、最小载荷、有效冲程、计算泵效、用电量和产量。
| 表 1 部分试验数据 |
为了避免在GRNN建模时输入或者输出变量中数值大和数值小的分量绝对误差差异大,对输入和输出分别进行归一化处理,使其归一化后的数据在-1到1之间。
4.2 GRNN抽油机生产系统建模经过上一步的处理,已经得到了两口井的建模数据,对两口井的数据分别取前面1 286组数据来训练模型,后面234组数据来验证模型的准确性。模型采用冲次、最大载荷、最小载荷、有效冲程、计算泵效5个变量作为输入,用电量和产量这2个指标作为输出。
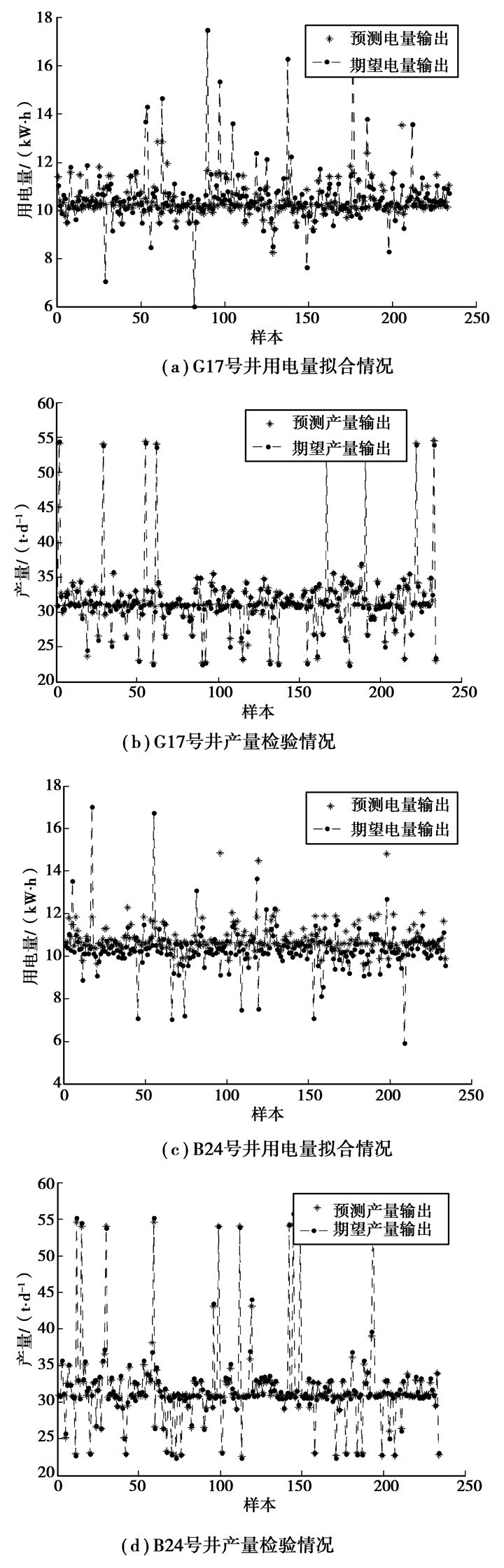
2个模型分别在光滑因子在0.3和0.4时,通过对模型的训练,拟合了油田抽油机采油系统的模型,检验数据带入模型得到的拟合效果如图 4所示,总体的均方差MSE和拟合优度U如表 2所示。
| 表 2 模型检验数据性能 |
从图 4可以看出,预测样本基本拟合了期望值,由表 2可见,MSE较小,U到达90%以上,网络模型具备了较强的泛化能力。可见,GRNN较好的拟合了抽油机系统的模型,建模效果良好。
|
图 4 GRNN模型检验数据拟合情况 |
在决策参数优化过程中,变量的上下限设根据经验设定,其设定结果如表 3所示,并设置VEPSO-BP算法的种群大小为100,迭代次数为50,2个学习因子都为2.5,神经网络的输出作为适应度函数,得到两口井的Pareto最优解集如图 5所示,两口井的Pareto前沿(仅列5组)如表 4所示。
| 表 3 变量上下限 |
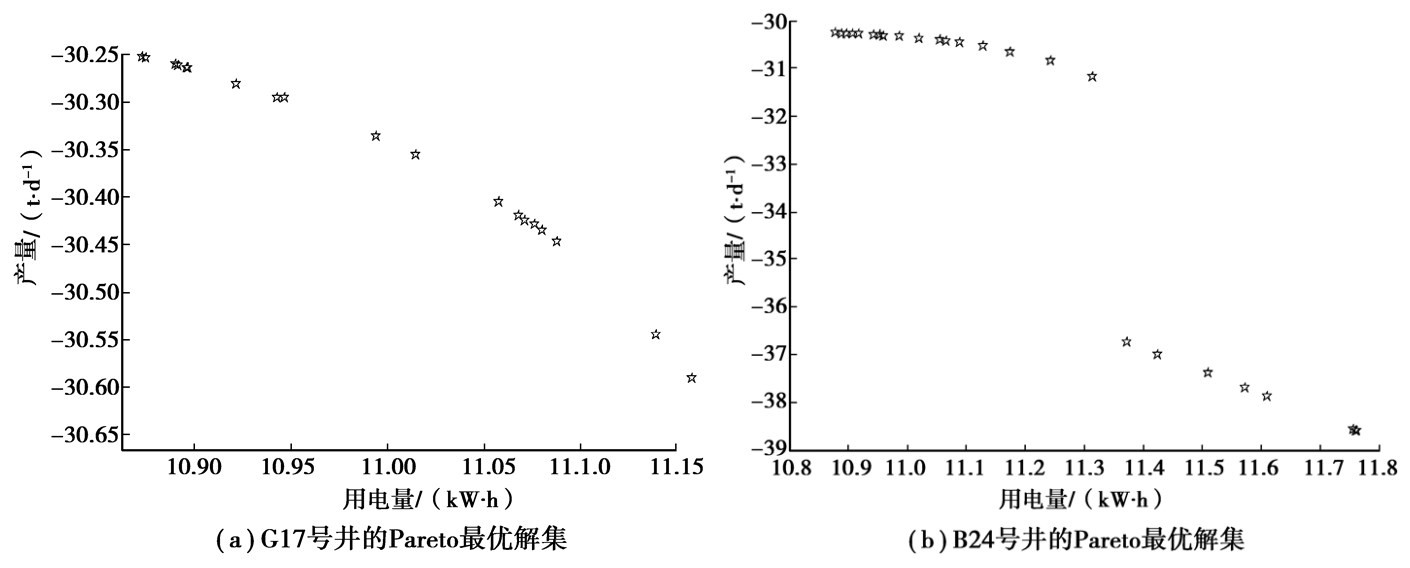
|
图 5 VEPSO-BP搜索的Pareto前沿 |
| 表 4 Pareto前沿 |
从图 5和表 4中可以看出,在2口井上分别得到了不同的Pareto前沿,方便了油田的工作人员在不同的操作环境下给出最优冲次。通过将获得的最优解带入实际的油田抽油机生产过程发现,经过优化后的生产过程大大降低了用电量的同时提高了产量,具体地G17号井用电量降低5.2%,产量提高了6.6%;B24号井用电量降低4.1%,产量提高了6.8%。实验结果充分证实了提出方法的可行性和有效性。
5 结论通过对抽油机采油系统的深入研究,建立了一套基于数据挖掘的抽油机建模及节能优化方法。首先,利用具有良好的非线性映射描述能力的GRNN建立了抽油机采油系统模型,然后,利用VEPSO-BP多目标优化算法搜索其最优决策参数,获得能节能降耗和增产的最优决策参数。实验结果表明本方法搜索到的最优决策参数用于油田生产,获得了6.6%以上的产量提高,和4.1%以上的用电量降低,实现了较大幅度的节能降耗。笔者提出方法对油田实现高产低耗的集约型生产提供了一种可行的解决思路,得到的是一个最优解集,如何从Pareto最优解集中找出一组最优解来指导生产,将是下一步研究的重点。
| [1] | Liu H L, Li Y, Huo G. Mechanical production parameters optimization and application[J]. Journal of Shengli Oilfield Staff University, 2007, 21(1): 30–31. |
| [2] | Xu J, L J, Chen J, Han M. Research on power saving positive torque and constant power pumping unit and tracking technique system[J]. Procedia Engineering, 2012, 29: 1034–1041. DOI:10.1016/j.proeng.2012.01.085 |
| [3] | Guo D M, Guan F, Zhu Y M, Liu Y Z. Improved design of CYJY12-4.8-73HB offset pumping unit support[J]. Journal of Oil and Gas Technology, 2005, 27(2): 258–260. |
| [4] | Gu Y H, Xiao W S, Zhou X X. Full scale test of ZXCY-series linear motor pumping units[J]. Petroleum Exploration and Development, 2008, 35(3): 366–372. DOI:10.1016/S1876-3804(08)60085-3 |
| [5] | Wang H F, Sun J M. Application of a single-speed three-power energy-saving motor in pumping unit[J]. Electric Machines & Control Application, 2010, 37(10): 50–54. |
| [6] | Li W, Yin Q, Cao J, Li L. The optimization calculation and analysis of energy-saving motor used in beam pumping unit based on continuous quantum particle swarm optimization[J]. Bio-Inspired Computing:Theories an Applications, 2010: 1–8. |
| [7] | Wang Q Y, Zhao H Q. The intelligent control technology and applications of rod pump well[J]. Petroleum Instruments, 2011, 25(1): 60–62. |
| [8] | Gao H B, Zhu Q F, Yang C J, et al. Intermittent intelligent pumping unit and its application[J]. China Petroleum Machinery, 2007, 35(11): 58–60. |
| [9] | Li M, He P, Meng C. The design of oil pump energy saving expert controller based on ARM[J]. Computing Technology and Automation, 2009, 28(4): 56–58. |
| [10] | Qi W, Zhu X, Zhang Y. Study of fuzzy neural network control of energy-saving of oil pump[C]. Proceedings of the CSEE, 2004, 137-140. https://link.springer.com/chapter/10.1007/978-3-540-87442-3_105 |
| [11] | Specht D F. A general regression neural network[J]. IEEE Transactions on Neural Networks, 1991, 2(6): 568–576. DOI:10.1109/72.97934 |
| [12] | Haidar A M A, Mustafa M W, Ibrahim F AF. Transient stability evaluation of electrical power system using generalized regression neural networks[J]. Applied Soft Computing, 2011, 22(4): 3558–3570. |
| [13] | Li H Z, Guo S, Li C J, Sun J Q. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm[J]. Knowledge-Based System, 2012, 08: 015. |
| [14] | Guo Y, Li N, Li X S. Multi-resource leveling in multiple projects and vector evaluated particle swarm optimization based on Pareto[J]. Control and Decision, 2010, 25(5): 789–793. |
| [15] | Zadedi G, Parvizian F, Rahimi M R. An expert model for estimation of distillation sieve tray efficiency based on artificial neural network approach[J]. Journal of Applied Science, 2010, 10(12): 1076–1082. DOI:10.3923/jas.2010.1076.1082 |
| [16] | Zou Y X. Production technology[M]. Peking: Petroleum Industry Press, 2006. |
 2013, Vol. 36
2013, Vol. 36

