目前非线性系统在微弱周期信号和噪声信号联合摄动下的混沌运动越来越受到人们的关注。基于混沌理论检测微弱信号是一个热门研究课题,也是混沌学发展的主要趋势,它的基本原理是混沌系统的非平衡相变对微弱信号有极强的敏感性以及对噪声有较强免疫力。信号检测包括频率、振幅和相位检测,频率检测是振幅和相位检测的前提同时也是一项困难的工作。对于信号的频率检测,文献[1]提出一种基于锁频原理的振子组检测方法,在Duffing方程的基础之上,采用78个级联振子阵列进行频率检测,该算法不仅复杂且只有当振子频率增加到某一成分信号频率附近时,才可以从时间图像上清晰观测到阵发混沌现象,但是检测方法繁琐。文献[2]提出一种循环相态技术,即统计一定时间内轨道定向穿过零点的次数,由固定的时间内得到周期的个数进而确定系统的频率,不足之处是没有考虑噪声对信号的影响。对于信号检测,人们目前用的较多的是Duffing振子[3-5],修正Duffing-Holmes振子[6]和双耦合Duffing振子[7],它们都属于非自治系统。利用非自治系统在理想的情况下进行信号检测尽管能获得较低的工作门限值,但是也存在一些不足。首先,此类系统一般采用计算过程较复杂的Melnikov函数作为判据来计算系统出现混沌的参数临界值,但Melnikov方法的分析结果不是充分条件[8],只能作为大致参考。依据此方法一般只能给出系统由周期状态进入混沌的参数条件,而实际检测时所采用的由混沌到大尺度周期的参数临界值无法直接计算,因此实际采用的参数常常与理论结果相差很大,获得合适的参数临界值要靠经验与尝试[9]。其次,非自治系统在强噪声影响下的分岔特性非常复杂,容易出现类似混沌状态的假象,造成错误判决,故只有当噪声功率很低时才能获得较好的检测效果[9]。以上这些问题是由非自治系统的固有特性决定的,仅通过对方程进行修正难以完全解决,因而有必要研究基于其它工作原理的新型自治混沌检测系统。
基于自治混沌系统的信号检测研究还较少,文献[10]基于非共振参数激励混沌抑制原理,利用受控Lorenz系统实现强噪声背景下微弱谐和信号的检测。文献[9]也利用该原理实现了强噪声背景下微弱周期脉冲信号的检测,但是该方法只能检测某种激励信号的存在性而不能精确地检测出信号的相关参数值。最近文献[11]采用高阶混沌振子及比例微分控制方法相结合,将含有待检信号的混沌振子从混沌态控制到周期态,然后利用频谱分析的方法检测待检信号的频率。从文献[11]的实验结果上看,最终检测出来的频率值在精确值附近的一个小范围内,通过肉眼观察检测频率值会导致一定的误差。
在以上研究成果的基础上,进一步研究利用自治混沌系统来检测噪声背景下信号频率的方法。首先,将含有噪声干扰的信号加入到一个自治混沌系统的某一项,此时系统的动力学特性更复杂,无法通过各种方法直接检测出待测信号的频率。因此,对受扰系统施加一个状态负反馈,通过适当地调节反馈控制增益,将系统的轨道控制到某一个极限环(由于受到噪声的干扰,极限环显得比较粗糙)。然后,利用文献[2]提出的循环相态技术,统计一定时间内受控轨道定向穿越某一个平面的总次数,再由固定的时间内得到周期的个数进而确定系统的振荡频率。由于系统的频率由待测信号的频率决定,而不受噪声的影响(噪声只会影响轨道的光滑程度),所以待测信号的频率也就是检测出的系统的振荡频率。仿真实验进一步验证了该方法的有效性,并对计算结果的绝对误差与相对误差进行分析,计算量小。
1 自治混沌系统的动力学行为研究 1.1 自治混沌系统模型利用文献[12]所提出的混沌系统来检测噪声背景下信号的频率,该系统的数学模型可以描述为
| $ \left\{ \begin{array}{l} \mathop {{x_1}}\limits^. = a({{x}_2} - {{x}_{^1}}),\\ \mathop {{x_2}}\limits^. = b{x_1} + c{x_2} + {x_1}{x_3},\\ \mathop {{x_3}}\limits^. = x_1^2 - h{x_3}, \end{array} \right. $ | (1) |
式中,x1,x2,x3为系统(1)的状态变量。当a=20,b=14,c=10.6,h=2.8,选取系统(1)的初始值为(1, 1, 1) 时,该系统存在一个典型的混沌吸引子,如图 1所示。
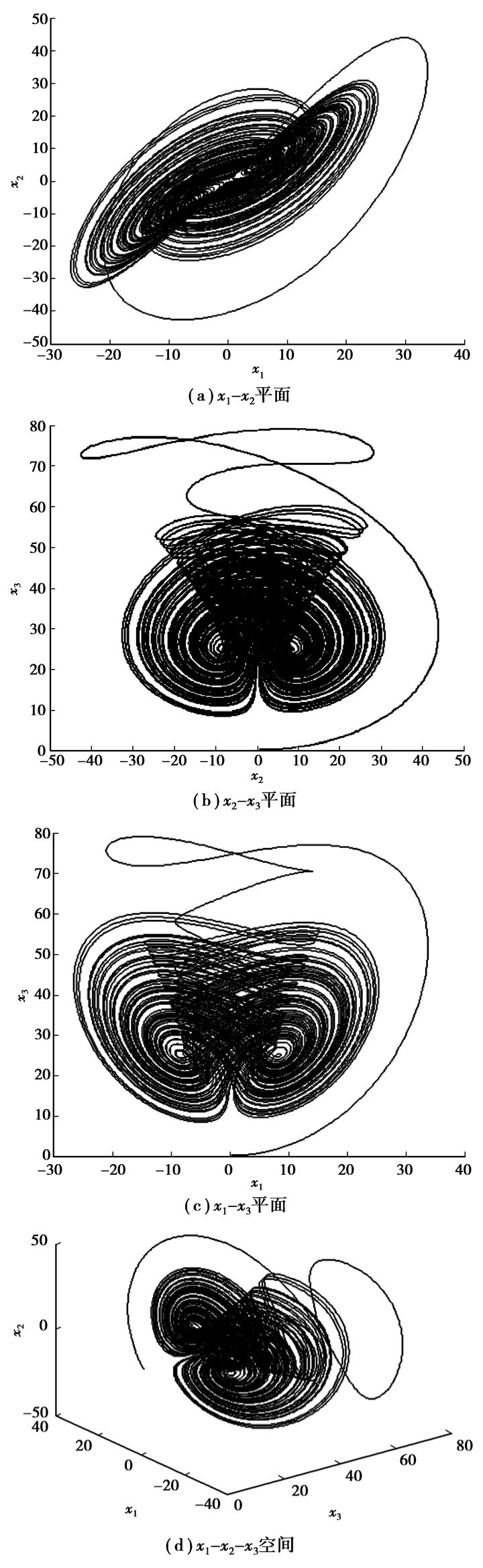
|
图 1 系统(1)的典型混沌吸引子的相图 |
混沌系统的基本特点就是系统对初始值的极端敏感性,2个相差无几的初值所产生的轨迹,随着时间的推移按指数方式分离,Lyapunov指数就是定量的描述这一现象的量。Lyapunov指数是衡量系统动力学特性的一个重要定量指标,它表征了系统在相空间中相邻轨道间收敛或发散的平均指数率。对于系统是否存在动力学混沌,可以从最大Lyapunov指数是否大于零非常直观的判断出来:一个正的Lyapunov指数,意味着在系统相空间中,无论初始两条轨线的间距多么小,其差别都会随着时间的演化而成指数率的增加以致达到无法预测,这就是混沌现象。为了进一步验证系统(1)在以上参数取值下确实存在混沌现象,数值计算出它的Lyapunov指数谱,如图 2所示。通过计算得到,系统(1)的Lyapunov指数分别为LE1=2.4040,LE2=0,LE3=-14.610 1,故系统(1)确实存在混沌现象。
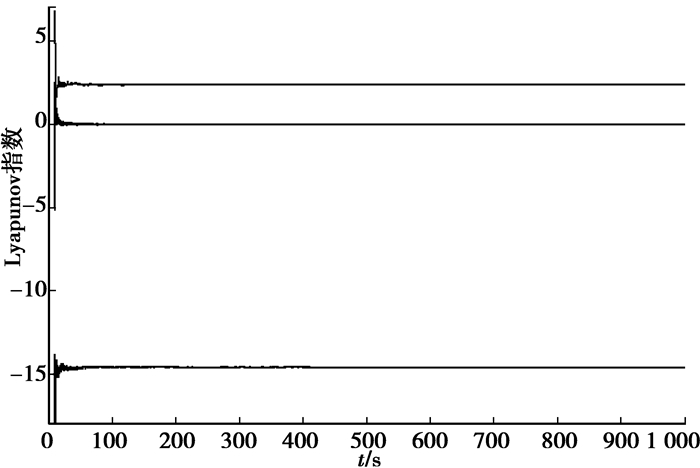
|
图 2 系统(1)的3个Lyapunov指数随时间的变化图 |
接下来,分析系统(1)的平衡点及其稳定性。令
在平衡点S0(0, 0, 0) 处,线性化系统(1),得到Jacobian矩阵为
| $ {\mathit{\boldsymbol{J}}_0} = \left[\begin{array}{l} -20\;\;\;\;20\;\;\;0\\ 14\;\;\;10.6\;\;0\\ \;0\;\;\;\;\;0\;\;\;-2.8 \end{array} \right], $ | (2) |
令det(J0-λI)=0,得其特征根为λ1=-2.8,λ2=17.973 6,λ3=-27.373 6。因为λ2是正实数,λ1和λ3是2个负实数,所以平衡点S0是第一类鞍点,故S0(0, 0, 0) 是不稳定的。
对平衡点S1(8.299 4,8.299 4,24.6) 和S2(-8.299 4,-8.299 4,24.6),注意到当(x1,x2,x3)变为(-x1,-x2,x3)时,系统(1)(x10,x20,x30)是系统(1)的解,则(-x10,-x20,x30)也是系统(1)的解,并且二解具有相同的性质,故分析其中之一即可。在此,分析平衡点S1的稳定性。在平衡点S1(8.299 4,8.299 4,24.6) 处,线性化系统(1),得到其Jacobian矩阵为
| $ {\mathit{\boldsymbol{J}}_1} = \left[ \begin{array}{l} -20\;\;\;\;\;\;\;\;\;\;20\;\;\;\;\;\;\;\;\;0\\ - 10.6\;\;\;\;10.6\;\;\; - 8.299\;4\\ 16.598\;8\;\;\;0\;\;\;\;\; - 2.8 \end{array} \right], $ | (3) |
令det(J1-λI)=0,得其特征根为λ1=-18.683 9,λ2=3.241 9+11.702 7i,λ3=3.241 9-11.702 7i。因为λ1是负实数,而λ2和λ3是一对具有正实部的共轭复根,所以平衡点S1是第二类鞍点,显然S2也是第二类鞍点,故平衡点S1、S2均是不稳定的。综上所述,平衡点S0、S1和S2都存在极限环。
2 噪声背景下信号频率的检测 2.1 噪声作用下的自治混沌系统设待检测的信号为s(t)=0.75cos(2πt)+n(t),其中待检信号的角频率为ω=2π,频率为f=1,幅值为0.75 V,n(t)=1×randn是均值为0,方差为1的噪声信号。从理论上说,将待测信号加入到系统(1)的3个方程的任意一个均可改变系统的动力学行为,将待测信号加入到系统(1)的第3个方程进行分析。于是,加入待测信号后的系统变为
| $ \left\{ \begin{array}{l} \mathop {{x_1}}\limits^. = a({{x}_2} - {{x}_{^1}}),\\ \mathop {{x_2}}\limits^. = b{x_1} + c{x_2} - {x_1}{x_3},\\ \mathop {{x_3}}\limits^. = x_1^2 - h{x_3} + s{\rm{(}}{t}{\rm{)}}, \end{array} \right. $ | (4) |
先取步长为0.002 π,仿真时间为t1=20 π,以初始值(x1(0),x2(0),x3(0))=(1.036 4,-0.673 9,0.458 9) 迭代得到一组值(x1(end),x2(end),x3(end))=(-4.947 2,-5.000 6,8.087 1);再以得到的(x1(end),x2(end),x3(end))为初始值,仿真时间为t2=40 π,求解系统(4),其相图如图 3所示。
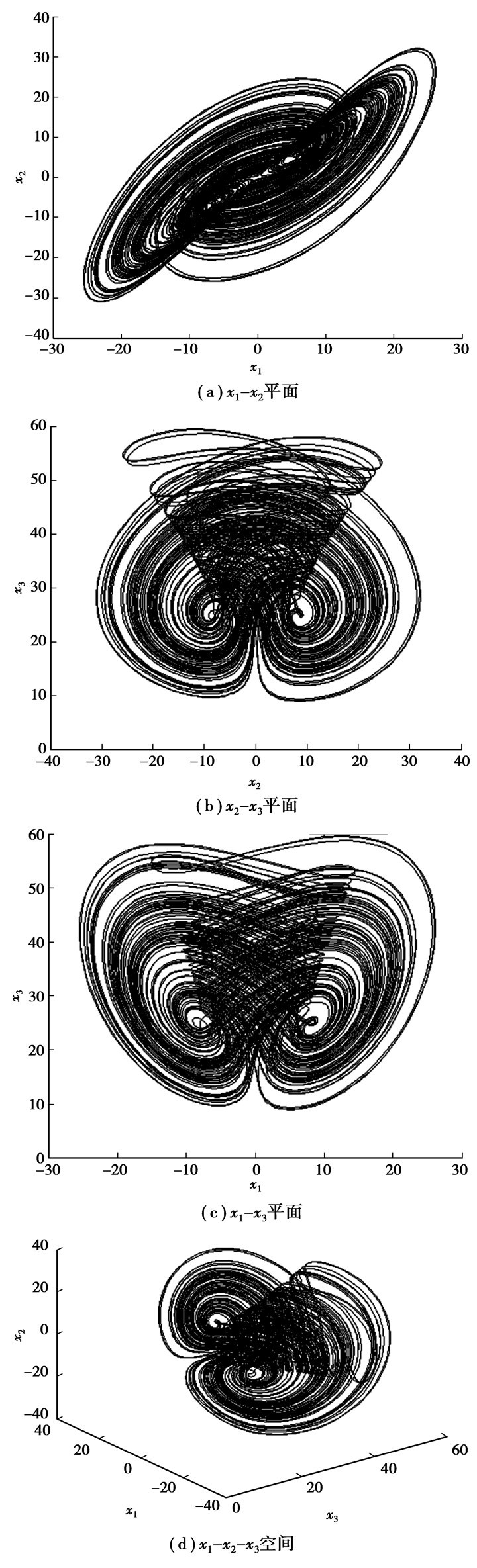
|
图 3 受扰系统(4) 的典型混沌吸引子的相图 |
从图 3的相轨迹来看,完全辨认不出输入信号中的待测周期信号,更无法通过频谱分析等方法观测出待测信号的频率。所以给系统(4) 的第2个方程增加一个负反馈项-kx2(t),通过不断调节反馈增益k的值,可以将系统(4) 控制到某一个比较粗糙的极限环(由于受到噪声的干扰)。通过实验尝试,这里取k=16.232 1,受控后的系统轨迹如图 4所示。

|
图 4 受扰系统(4) 在负反馈-kx2(t)控制下的轨迹相图 |
利用文献[2]提出的一种定向循环相态技术,统计在后40 π时间内从左到右定向穿越平面x2(t)=-4.85(如图 4(b)所示)的总次数为Times=126次,所以待测信号的频率估计为
| $ \begin{array}{l} \;\;\;\mathop f\limits^ \wedge = \frac{1}{{\mathop T\limits^ \wedge }} = 1/({{t}_2}/{\rm{Times}}) = \\ 1/(40{\rm{\pi /{\rm{Times}}}}) = 1.002\;676。\end{array} $ |
该检测方法得到的绝对误差eab=|f-
当检测信号都取s(t)=0.75cos(2πft)+σ2randn时,针对不同噪声方差情形下,得到以下检测结果,如表 1所示。
| 表 1 不同噪声的影响下,待测信号频率检测结果 |
从表 1可以看出:即使在不同强度的噪声干扰下,利用该方法的检测结果对噪声具有较强的免疫力,而且检测误差较小,从而表明了该方法的可行性和有效性。
3 结论针对噪声背景下的信号检测问题,提出一种利用自治混沌系统来检测信号频率的新方法。该方法克服了利用非自治混沌系统检测信号时的不足—获得合适的参数临界值要靠经验与尝试和容易出现类似混沌状态的假象,容易造成错误判决。同时提出的方案也有利于借鉴在自治混沌系统的控制领域中已取得的大量研究成果,为微弱信号的混沌检测方法提供新的途径。实验仿真结果表明,提出的方法能够检测出噪声背景下的微弱正弦信号的频率,且精度较高。利用自治系统来检测噪声背景下信号的幅值和相位是进一步的工作。
| [1] | Wang G Y, Chen D J, Chen X. The application of chaotic oscillators to weak signal detection[J]. IEEE Tansactions on industrial electronics, 1999, 46(2): 440–444. DOI:10.1109/41.753783 |
| [2] | 李月, 杨宝俊. 混沌振子系统(L-Y)与检测[M]. 科学出版社, 2007. |
| [3] |
王冠宇, 陶国良, 陈行, 等.
混沌振子在强噪声背景信号检测中的应用[J]. 仪器仪表学报, 1997, 18(2): 209–212.
WANG Guanyu, TAO Guoliang, CHEN Xing, et al. The application of chaotic oscillator in high noise background signal detection[J]. Chinese Journal of Scientific Instrument, 1997, 18(2): 209–212. (in Chinese) |
| [4] |
赵向阳, 魏明献, 刘君华.
基于混沌技术的频率测试仪的研制[J]. 测试技术学报, 2004, 18(2): 156–161.
ZHAO Xiangyang, WEI Mingxian, LIU Junhua. Development of frequency test instrument based on chaos technology[J]. Journal of Test and Measurement Technology, 2004, 18(2): 156–161. (in Chinese) |
| [5] | Li Y, Yang B J, Du L Z, et al. The bifurcation threshold value of the chaos detection system for a weak signal[J]. Chinese Physics, 2003, 12(7): 714–720. DOI:10.1088/1009-1963/12/7/304 |
| [6] |
李月, 杨宝俊.
检测强噪声背景下周期信号的混沌系统[J]. 科学通报, 2003, 48(1): 19–20.
LI Yue, YANG Baojun. Strong background noise detection of periodic signal chaotic systems[J]. Chinese Science Bulletin, 2003, 48(1): 19–20. (in Chinese) |
| [7] |
李月, 路朋, 杨宝俊, 等.
用一类特定的双耦合Duffing振子系统检测强色噪声背景中的周期信号[J]. 物理学报, 2006, 55(4): 1672–1679.
LI Yue, LU Peng, YANG Baojun, et al. Applying a special kind of two coupled Duffing oscillator system to detect periodic signals under the background of strong colored noise[J]. Acta Physica Sinica, 2006, 55(4): 1672–1679. DOI:10.7498/aps.55.1672 (in Chinese) |
| [8] | 刘曾荣. 混沌的微扰判据[M]. 上海科技教育出版社, 1994. |
| [9] |
王德石, 谌龙, 史跃东.
基于受控Lorenz系统的微弱脉冲信号检测[J]. 动力学与控制学报, 2010, 8(1): 48–52.
WANG Deshi, SHAN Long, SHI Yuedong. Detection of weak pulse signals based on a controlled Lorenz system[J]. Journal of Dynamics an Control, 2010, 8(1): 48–52. (in Chinese) |
| [10] |
谌龙, 王德石.
基于Lorenz系统的微弱谐和信号检测[J]. 仪器仪表学报, 2010, 28(11): 2034–2038.
SHAN Long, WANG Deshi. Detection of weak Harmonic signals in strong noise based on Lorenz system[J]. Chinese Journal of Scientific Instrument, 2010, 28(11): 2034–2038. (in Chinese) |
| [11] |
徐艳春, 杨春玲.
高阶混沌振子的微弱信号频率检测新方法[J]. 哈尔滨工业大学学报, 2010, 42(3): 446–450.
XU Yanchun, YANG Chunling. New method of weak signal frequency detection using high-level Chaotic oscillator[J]. Journal of Harbin Institute of Technology, 2010, 42(3): 446–450. DOI:10.11918/j.issn.0367-6234.2010.03.025 (in Chinese) |
| [12] |
蔡国梁, 谭振梅, 周维怀, 涂文桃.
一个新的混沌系统的动力学分析及混沌控制[J]. 物理学报, 2007, 56(11): 6230–6238.
CAI Guoliang, TAN Zhenmei, ZHOU Weihuai, et al. Dynamical analysis of a new chaotic system and its chaotic control[J]. Acta Physica Sinica, 2007, 56(11): 6230–6238. (in Chinese) |
| [13] | Wang J G, Zhou J Z, Peng B. Weak signal detection method based on Duffing oscillator[J]. Chaos, 2010, 20(1): 53–58. |
| [14] | Zozor S, A P O. On the use of stochastic in sine detection[J]. Signal Processing, 2002, 82(3): 353–367. DOI:10.1016/S0165-1684(01)00174-8 |
| [15] | Birxd I. Chaotic oscillators and CMFFNS for signal detection in noise environments[J]. IEEE International Joint Conference on Neural Networks, 1992, 22: 881–888. |
| [16] | Song C Y, Lei Y H, Ding S Q. Application of chaos to weak signal detection[J]. Editorial Board of Journal of Harbin Engineering, 2004, 25: 21–23. |
| [17] | Choe C U, Hohne K, Benner H, et al. Chaos suppression in the parametrically driven Lorenz system[J]. Physical Review, 20005, 72(5): 362–366. |
| [18] | Song C Y, Huang W T, Lin F P, et al. Controlling chaos with weak periodic signals optimized by a genetic algorithm[J]. Physical Review, 2004, 70: 1519–1537. |
| [19] | Nie C Y, Shi Y W, Wang Z W, et al. A detection method of signal frequency based on optimization theory[C]//Sixth International Symposium on Instrumentation and Control Technology:Signal Analysis, Measurement Theory, Photo-Electronic Technology and Artificial Intelligence. Beijing:[s. n.]. 2006:323-327. |
 2013, Vol. 36
2013, Vol. 36

