微能源系统(Power MEMS)功率密度比目前最好的Liso2电池系统高20~30倍,在MAV(micro air vehicles)、UAVs(unmanned aerial vehicles)、可携带能源(可携带电脑、手机、GPS接收器等器件的电池系统)等领域都有广泛的应用前景[1-2]。典型的微能源系统包括:MIT的径向微型涡轮发动机[3-4]、Berkeley的微型转子发动机[5]、Georgia Tech的微型自由活塞式发动机等[6]、NASA资助的微型蒸汽轮机[7]、东京大学的轴径向微型涡轮发动机等[8]。
MIT和东京大学的微型涡轮发动机内部关键涡轮结构都来自于对宏观涡轮发动机结构的直接微型化,结构复杂,受制于微加工工艺、材料等的限制以及相关理论的不完善,目前还处于证实其可行性阶段。
笔者发展出周向微型涡轮,该涡轮采用新的动叶叶型设计理念,设计为周向进气,静叶由涡轮外的喷管代替,结构简单,适应于微型化[9-11]。在整个周向进气微型涡轮系统中,高压氢气首先通过第一、二级引射器,同时卷吸空气形成混合燃气;混合气体在燃烧室中充分燃烧,温度急剧上升;燃烧尾气通过第三级引射器时卷吸大量空气,尾气温度降低、流量提高;接着混合气体经过喷管并膨胀针对发展出的六叶片周向微型涡轮,对其内部流动进行全三维瞬态数值仿真,分析其流动特性,对其结构进行评价[12-13]。对涡轮叶顶间隙对压力损失的影响进行仿真分析[14]。最后对六叶片微型涡轮和改进出的八叶片微型涡轮的输出性能进行仿真和实验对比分析。
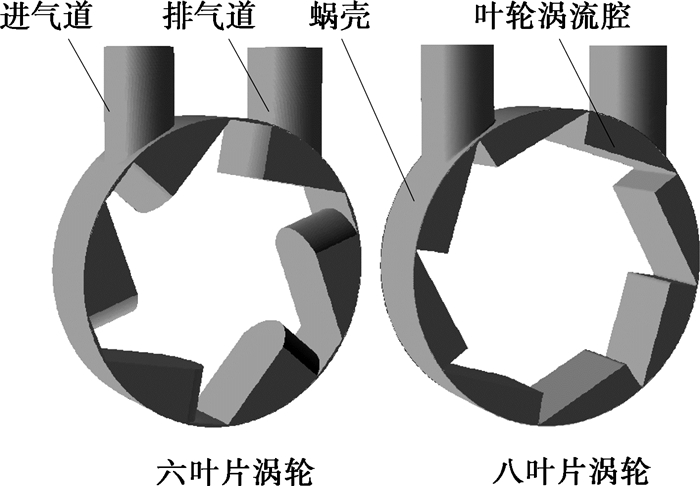
1 偏微分方程及算法系统能量转换的关键部位是涡轮,对涡轮内部工质流动进行全三维瞬态数值仿真,图 1为周向微型涡轮模型图。几何模型包括静止的进气道、排气道区域、蜗壳静止区域和旋转的叶轮涡轮腔流体区域。由于叶轮顶部间隙和两侧端部间隙非常小,受数值计算收敛性对网格长宽比的要求,总网格数量非常大且间隙处网格占绝大部分。受计算资源的限制,最终模型中没有考虑两侧端部漏气。
|
图 1 周向微型涡轮几何模型 |
涡轮内部工质的流动包括间隙泄漏流动、二次流、漩涡等复杂流动,并且受涡轮旋转离心力的影响,涡轮内部的流动结构复杂,且具有高应变率和流线弯曲程度大的特点,所以仿真采用RNG k-e双方程模型,对于近壁区采用标准壁面函数法来处理。工质湍流流动过程遵守质量守恒和动量守恒定律,控制方程如下。
质量守恒方程
| $ \frac{{\partial \rho }}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{v}}} \right) = 0。$ | (1) |
动量守恒方程
| $ \frac{{\partial \left( {\rho \mathit{\boldsymbol{v}}} \right)}}{{\partial t}} + {\rm{div}}\left( {\rho \mathit{\boldsymbol{v}}\upsilon } \right) = {\rm{div}}\left( {\mu {\rm{grad}}\mathit{\boldsymbol{v}}} \right)-\frac{{\partial p}}{{\partial x}} + s。$ | (2) |
式中:ρ为密度;v为速度矢量; p为流体压力; μ为流体的动力黏度; s为动量方程广义源项。
湍流模型采用时均形式的微分方程, 在充分发展的湍流区域, 反映湍流脉动量对流场影响的湍动能方程和耗散率方程如下。
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho k{u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[{{a_{\rm{k}}}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_i}}}} \right] + }\\ {{G_{\rm{K}}} + {G_{\rm{b}}} -\rho \varepsilon ,} \end{array} $ | (3) |
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon {u_i}} \right)}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[{{a_\varepsilon }{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + }\\ {C_{1\varepsilon }^*\frac{\varepsilon }{k}{G_{\rm{K}}} -{C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k},} \end{array} $ | (4) |
其中:μeff=μ+μt;
| $ \begin{array}{l} C_{1\varepsilon }^* = {C_{1\varepsilon }}- \frac{{\eta \left( {1- \frac{\eta }{{{\eta _0}}}} \right)}}{{1 + \beta {\eta ^3}}};\\ \eta = {\left[{\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) \cdot \left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right)} \right]^{\frac{1}{2}}}\frac{\kappa }{\varepsilon };\end{array} $ |
k为湍流动能; ε为湍流耗散率; μt=ρCμk2 /ε, μt为湍流黏度; Cμ=0.084 5, ak=aε=1.39; Gk为由于平均速度梯度引起的湍动能k的产生项; C1ε、C2ε、分别为经验常数, C1ε=1.42, C2ε=1.68; η0=4.377, β=0.012。
采用PISO算法计算,数值离散格式采用有限体积法,压力离散采用PRESTO差分格式, 其余采用二阶迎风格式,时间离散采用二阶隐式差分格式。
2 动网格处理采用滑动网格技术处理这种周期性旋转问题,滑动网格模型允许相邻网格间发动相对运动,且交界面网格可以是非正则的。所以在设置好一对交界面后,便可以对不同计算区域设置不同的运动状态,而壁面和交界面只需要设置成无滑移边界条件便可随相邻的计算区域一起运动,实现对涡轮旋转运动的仿真。在计算网格界面上的通量时,要考虑网格间的相对运动对其的影响,实际计算时,每迭代一次就更新一次网格界面和网格界面的重叠区域。用重叠区域的网格来计算流场变量穿过交界面的通量,而不是用交界面上的网格计算,以此实现动网格对流场影响的仿真。
采用混合网格对整个计算域分区剖分,分为进气道和排气道区域、蜗壳内静止区域和叶轮旋转区域,进排气道与蜗壳内静止区域之间由内边界连接,蜗壳静止区域与叶轮旋转区域由滑动交界面连接,进排气道区域网格密度较小,后两个区域网格密度较大,并对近壁区加密网格,网格总数约91E4。边界条件入口为质量流量入口,出口为静压,蜗壳区域壁面为静止壁面,叶轮区域壁面随叶轮同步旋转,六叶片涡轮60°转角为一个旋转周期,八叶片涡轮45°转角为一个旋转周期。
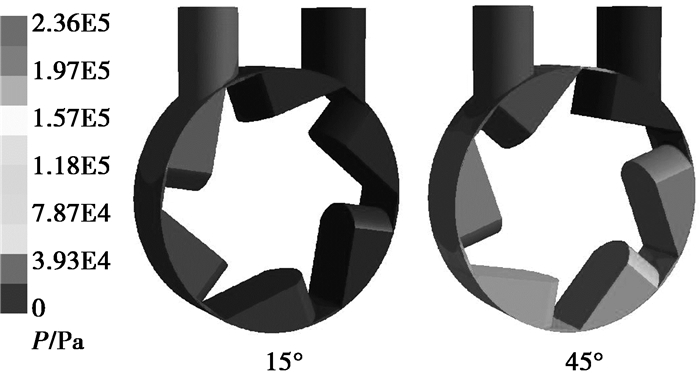
3 数值仿真结果分析 3.1 涡轮内部流场分析图 2、3为六叶片涡轮一个工作周期内不同时刻的流场剖面图和整体压力图,图中工质从左侧进气道进入涡轮内部工作腔冲击涡轮叶片逆时针旋转,发现两叶片间弧长大于进气道与出气道之间的机壳弧长,导致在0°~30°转角范围内排气道与进气道直接连通,部分工质未做功就进入了排气道直接排出,有效冲击叶轮的工质平均速度较低,低于25 m/s,漏气损失较大,图中15°转角速度云图明显可以看到部分工质直接进入排气道排出。对应时刻压力图显示进出口压差急剧减小,在15°转角时压差减至约4E4 Pa,仿真显示最低压差为2E4 Pa。在30°~60°转角范围内,叶片与外壳形成相对密闭空间,除微量叶顶漏气外,工质都对涡轮做功,对应时刻进出口压差迅速增大,到45°转角时,进出口压差已达到2E5 Pa。最大进出口压差约为2.3E5 Pa。综上分析,六叶片涡轮在结构上存在缺陷。
|
图 2 六叶片涡轮工质压力分布 |

|
图 3 六叶片涡轮工质流速分布 |
另外,六叶片涡轮设计的圆柱面叶型目的是为了增加受冲击面积,以提高工质做功,但从仿真得到的流场细节来看,工质冲击曲面,在曲面上产生了沿叶轮轴向的力矩分量,并且轴向两侧力矩分量大致互相抵消,所以总的效果并不理想。而另一方面,这种复杂的几何形状结构的零件制造性和工艺性较差,都是由数控机床和专用的数控分度设备完成的,加工时间和成本都相当高。
考虑六叶片涡轮的设计缺陷,改进出八叶片涡轮,将涡轮由原来的6个叶片增加到8个,使两叶片间弧长小于进气道与出气道之间的机壳弧长,这样涡轮工作中始终保持封闭工作空间,防止工质大量漏气,同时使叶片受到高速气流冲击的频率增加30%,以更充分地利用工质做功。将原局部圆柱面叶型改成普通的平面叶型,这样八叶片涡轮可制成一体,采用耐高温高分子材料一次性整体注塑成型,改变了原气动涡轮转子金属切削加工工艺过程,提高了生产效率,且降低了制造成本。
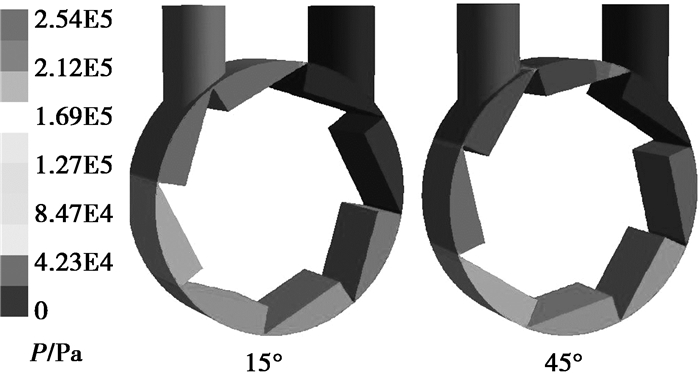
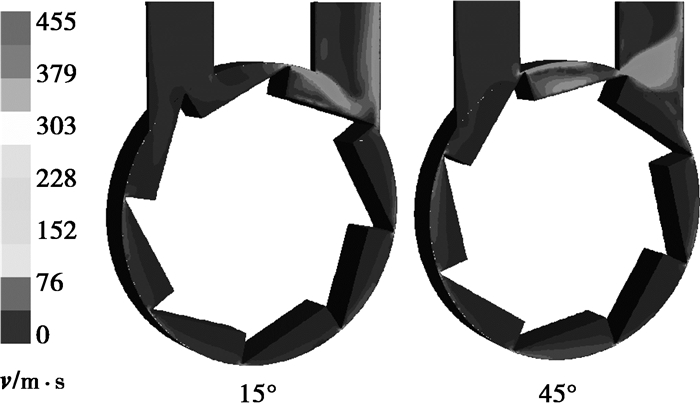
设置八叶片涡轮仿真边界条件同六叶片涡轮,部分转角下工质速度分布及进出口压力如图 4、5所示。与六叶片涡轮相比,在一个工作周期内,除了微量叶顶漏气外,未出现类似的大量漏气现象。工作腔内工质平均速度大于30 m/s,压力图显示,最大进出口压差位于45°转角附近,约为2.5E5 Pa,15°转角时进出口压差约2.2E5 Pa,最小进出口压差约2.0E5 Pa,工作周期内压力波动较小。八叶片涡轮腔内工质平均速度和压力都大于六叶片。
|
图 4 八叶片涡轮工质压力分布 |
|
图 5 八叶片涡轮工质流速分布 |
图 6为八叶片涡轮叶顶相对间隙对压力损失的影响,在相对间隙小于0.01后,压力损失对间隙非常敏感,间隙减小到0.005时,压力损失已增大到2.53E5,比0.01间隙时压差提高了一个数量级,而在间隙为0.01~0.02时,压力损失随间隙变化相对较小,当间隙大于0.02后,其对压降的影响已经非常小。
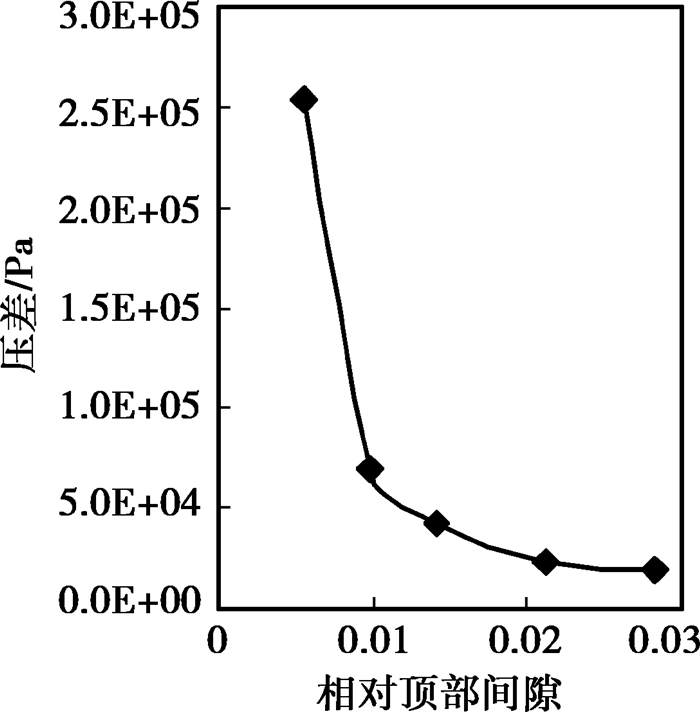
|
图 6 叶顶相对间隙对压力损失的影响 |
为对比分析八叶片涡轮和六叶片涡轮对外输出性能和验证仿真结果,实验测试两种涡轮样机对外输出转速和机械功率[15],以测得的流量和转速数据为数值仿真边界条件,仿真获取涡轮对外输出机械功率。
图 7为实验测得的两种涡轮样机转速随涡轮入口工质流量变化数据。图中显示,六叶片涡轮和八叶片涡轮转速随流量变化的规律具有相似性,都随流量的增大而增大,且转速与流量呈现非线性关系。相同入口流量下八叶片涡轮转速高于六叶片涡轮,实验测得的八叶片涡轮最高转速为6.5E5 r/min,后者为4.7E5 r/min。八叶片涡轮的启动流量为140 L/h,六叶片涡轮启动流量为200 L/h。
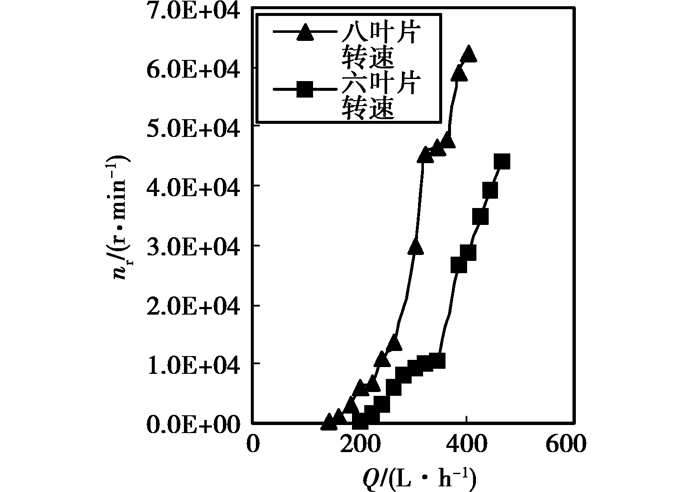
|
图 7 涡轮对外输出转速随流量的关系(实验数据) |
图 8为六叶片涡轮对外输出机械功率的实验和仿真对比图。图中显示,实验结果和仿真结果具有相同的变化趋势,输出机械功率都随流量的增大而增大,但所有流量下仿真数据均略大于实验数据。分析认为,主要是由于仿真没有考虑涡轮两侧端部漏气,结果中不包含端部漏气损失和漏气带来的粘性摩擦损失所致。图中还显示,仿真结果和实验结果都在超过200 L/h时开始输出机械功率,在200 L/h到370 L/h流量段,机械功率随流量变化较缓慢,超过370 L/h,机械功率随流量变化速率明显增大。实验最大机械功率为1 226 mW,仿真值为1 408 mW。
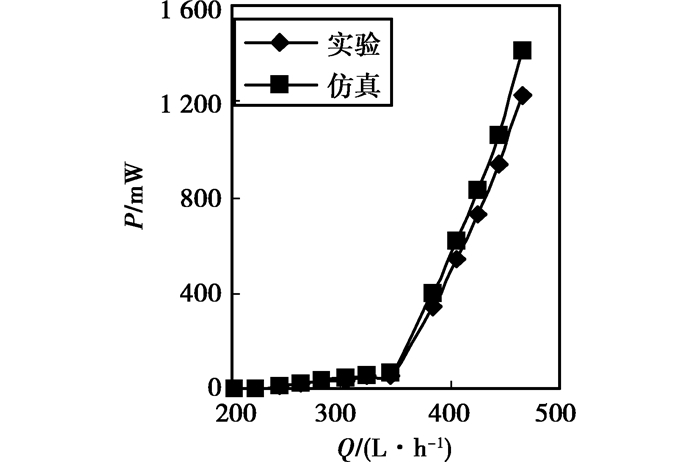
|
图 8 六叶片涡轮机械功率试验与仿真对比 |
图 9为八叶片涡轮对外输出机械功率的实验和仿真对比图。图中显示,与六叶片涡轮结果类似,所有流量下仿真结果均略大于实验结果,原因同六叶片涡轮一样,仿真数据与实验数据具有相同的变化趋势,随流量的增大而增大。八叶片涡轮输出机械功率的启动流量为140 L/h,小于六叶片涡轮的200 L/h。在140 L/h到280 L/h流量段,机械功率随流量变化比较缓慢,此后功率随流量变化速率显著增大。八叶片涡轮实验最大机械功率为1 355 mW,较六叶片涡轮提高10.5%,八叶片涡轮仿真最大机械功率为1 540 mW,较六叶片涡轮提高9.4%。
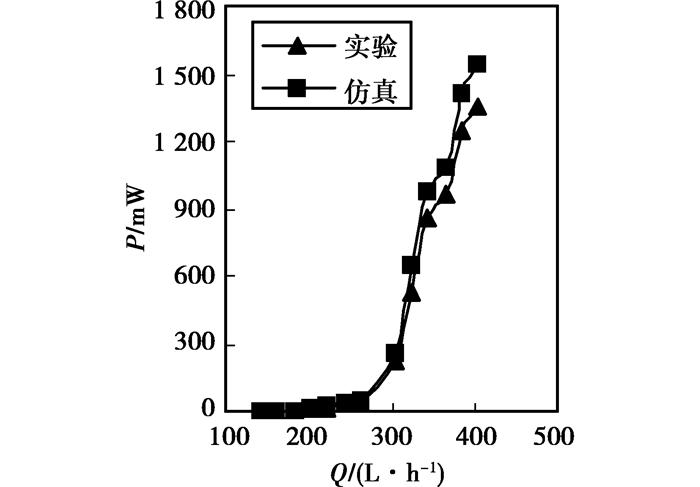
|
图 9 八叶片涡轮机械功率试验与仿真对比 |
对发展出的六叶片周向微型涡轮和八叶片微型涡轮内部工质流动和叶顶间隙对压降的影响进行数值分析,并对涡轮机械功率进行仿真和实验对比分析,得出结论如下:
1) 六叶片涡轮存在结构缺陷,运转时进出口周期性连通,部分工质未做功即排出。改进的八叶片涡轮没有上述缺陷,八叶片涡轮腔内工质平均速度和压力都大于六叶片涡轮。
2) 叶顶相对间隙对压力损失的影响呈现非线性关系,在间隙小于0.01后,压力损失对间隙变化非常敏感,而在间隙为0.01~0.02时,压力损失随间隙变化相对较小,当间隙大于0.02后,其对压降的影响已经非常小。
3) 八叶片涡轮性能优于六叶片涡轮,仿真结果和实验结果都显示,八叶片涡轮和六叶片涡轮机械功率随工质流量的增加而增加。八叶片涡轮最大机械功率为1 355 mW,较六叶片涡轮提高10.5%,八叶片涡轮机械功率启动输出的流量为140 L/h,小于六叶片涡轮的200 L/h。
| [1] | Chou S K, Yang W M, Chua K J, et al. Development of micro power generators:a review[J]. Applied Energy, 2011, 88(1): 1–16. DOI:10.1016/j.apenergy.2010.07.010 |
| [2] | Jacobson S A, Epstein A H. An informal survey of power MEMS[C/OL]//Proceedings of the International Symposium on Micro-Mechanical Engineering, December 1-3, 2003, Tsuchiura, Japan.[2012-05-10]. http://www.ttivanguard.com/montrealreconn/powerMEMS.pdf. |
| [3] | Spadaccini C M, Mehra A, Lee J, et al. High power density silicon combustion systems for micro gas turbine engines[J]. Journal of Engineering for Gas Turbines and Power, 2003, 125(3): 709–719. DOI:10.1115/1.1586312 |
| [4] | Epstein A H. Millimeter-scale, micro-electro-mechanical systems gas turbine engines[J]. Journal of Engineering for Gas Turbines and Power, 2004, 126(2): 205–226. DOI:10.1115/1.1739245 |
| [5] | Fernandez-Pello A C, Pisano A P, Fu K, et al. MEMS rotary engine power system[J]. IEEJ Transactions on the Sensors and Micromachines, 2003, 123(9): 326–330. DOI:10.1541/ieejsmas.123.326 |
| [6] | Suzuki Y, Okada Y, Ogawa J, et al. Experimental study on mechanical power generation from MEMS internal combustion engine[J]. Sensors and Actuators A:Physical, 2008, 141(2): 654–661. DOI:10.1016/j.sna.2007.08.020 |
| [7] | Frechette L G, Lee C G, Arslan S, et al. Design of a microfabricated Rankin cycle steam turbine for power generation[J]. American Society of Mechanical Engineers, 2003, 5: 335–344. |
| [8] | Matsuo E, Yoshiki H, Nagashima T, et al. The development of the ultra micro gas turbines[J]. Journal of the Japan Institute of Energy, 2005, 84(3): 192–199. |
| [9] | Zhang L, Chen W J, Deng D Q. Research on principle of quasi gas power cycle for Power MEMS[C]//Proceedings of the International Conference on Mechanical Transmissions, September 26-30, 2006, Chongqing University, Chongqing, China. Beijing:Science Press, 2006:1120-1126. |
| [10] |
王婧, 张力, 邓达强, 等.
准气体动力循环Power MEMS气体静压轴承的研究[J]. 重庆大学学报:自然科学版, 2007, 30(7): 18–21.
WANG Jing, ZHANG Li, DENG Daqiang, et al. Research on static pressure bearing of quasi gas power cycle for Power MEMS[J]. Journal of Chongqing University:Natural Science Edition, 2007, 30(7): 18–21. (in Chinese) |
| [11] | 张力, 陈卫军, 李坚. 微型发动机: 中国, CN200610054004. 3. [P]. 2006-08-09. |
| [12] |
许开富, 乔渭阳, 罗华玲.
涡轮叶尖间隙流动的数值模拟[J]. 热能动力工程, 2009, 24(4): 432–436.
XU Kaifu, QIAO Weiyang, LUO Hualing. Numerical simulation of turbine blade tip leakage flow[J]. Journal of Engineering for Thermal Energy and Power, 2009, 24(4): 432–436. (in Chinese) |
| [13] |
陈进, 张石强, 陆群峰, 等.
泛函分析思想在新型风力机叶片设计中的应用[J]. 重庆大学学报, 2011, 34(7): 14–19, 27.
CHEN Jin, ZHANG Shiqiang, LU Qunfeng, et al. The application of functional theory to the design of new wind turbine blades[J]. Journal of Chongqing University, 2011, 34(7): 14–19, 27. DOI:10.11835/j.issn.1000-582X.2011.07.003 (in Chinese) |
| [14] |
宋立权, 赵学科, 李智成, 等.
旋叶式压缩机叶片运动学理论研究与仿真[J]. 重庆大学学报, 2011, 34(8): 60–65.
SONG Liquan, ZHAO Xueke, LI Zhicheng, et al. Blade kinematical theory for rotary vane compressor[J]. Journal of Chongqing University, 2011, 34(8): 60–65. DOI:10.11835/j.issn.1000-582X.2011.08.011 (in Chinese) |
| [15] | Liao Z B, Zhang L, Xu Z J, et al. Development and experimental investigation of micro-turbine in millimeter size[J]. Materials Science Forum, 2009, 628/629: 357–362. DOI:10.4028/www.scientific.net/MSF.628-629 |
 2013, Vol. 36
2013, Vol. 36


