生产调度是生产管理的核心内容和关键技术,是一种复杂的组合优化问题,属于NP-hard问题[1]。自动化电镀生产线调度较传统的作业生产车间调度,除了需要考虑工件的调度,还需考虑电镀行车的调度,调度模型更加复杂。目前遗传算法(GA)、蚁群算法(ACA)等智能算法已广泛应用于生产调度的研究[2-4];禁忌搜索(TS),免疫算法(IA)等智能优化也受到研究者的关注[5-7]。GA研究相对成熟,但存在易早熟,局部搜索能力差等弱点,克隆算法(CSA)与GA类似,采用群体搜索和操作算子策略,具有邻域局部性信息继承与逼近的特点[8],搜索目标具有一定的分散性、独立性[9]。CSA虽然克服了遗传算法局部搜索能力差的问题,但常出现进化缓慢现象,局部搜索能力与全局搜索能力相矛盾[10-11]。鉴于此,笔者提出了克隆概率和变异概率与迭代次数相关的自适应克隆竞争算法,寻优初期,抗体种群差异较大,优良个体所占比重小,较大的变异概率和较小的克隆概率能增加种群多样性,扩大搜索空间,增强全局最优的搜索能力,随着迭代次数的增加,种群优良性增强,较小的变异概率和较大的克隆概率能保持种群优良性,提高收敛精度。
1 自动化电镀生产线多目标调度模型 1.1 自动化电镀生产线调度模型自动化电镀生产线调度问题描述为:有n批工件,m个镀槽(包含并行工位),工件在各镀槽中的加工时间和加工顺序确定,h辆行车,负责工件在各镀槽间的转移,假设和约束条件如下:
1) 工件一旦进入生产,则不能中断,且镀槽之间无中间缓冲区,即
| $ \begin{array}{*{20}{c}} {{t_{{\rm{f}}kj}} = {t_{{\rm{s}}kj}} + {t_{kj}},}\\ {j \in \left( {1,m} \right);k \in \left( {1,n} \right),} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {{t_{{\rm{s}}k{j_2}}} = {t_{{\rm{f}}k{j_1}}} + \frac{{{l_{{j_1},{j_2}}}}}{v} + {t_{\rm{r}}},}\\ {{j_1} \in \left( {1,m} \right);{j_2} \in \left( {{j_1} + 1,m} \right);k \in \left( {1,n} \right),} \end{array} $ | (2) |
式中:tfkj为工件k在j中的完工时间;tskj为工件k在j中的开工时间;tkj为工件k在j中的加工时间;lx1, x2为镀槽j1到j2的中心距离;v为行车带料时的移动速度;tr为行车取料、放料时间和。
2) 同一镀槽在同一时间加工工件数目不能超过1[12-13]:
| $ \begin{array}{*{20}{c}} {\left| {{t_{{\rm{f}}{k_1}j}} - {t_{{\rm{f}}{k_2}j}}} \right| + \left| {{t_{{\rm{s}}{k_1}j}} - {t_{{\rm{s}}{k_2}j}}} \right| \ge {t_{{k_1}j}} + {t_{{k_2}j}},}\\ {j \in \left( {1,m} \right);{k_1},{k_2} \in \left( {1,n} \right);{k_1} \ne {k_2}。} \end{array} $ | (3) |
当工序存在并行工位时,设并行工位中最先完成加工的工件在此工位上的加工时间、开始时间以及结束时间分别为s′kj、f′kj,则应满足:
| $ \begin{array}{*{20}{c}} {\left| {{{t'}_{{\rm{f}}{k_1}j}} - {{t'}_{{\rm{f}}{k_2}j}}} \right| + \left| {{{t'}_{{\rm{s}}{k_1}j}} - {{t'}_{{\rm{s}}{k_2}j}}} \right| \ge {{t'}_{{k_1}j}} + {{t'}_{{k_2}j}},}\\ {j \in \left( {1,m} \right);{k_1},{k_2} \in \left( {1,n} \right);{k_1} \ne {k_2}。} \end{array} $ | (4) |
3) 同一时间,行车最多能转移一批工件:
| $ \left\{ \begin{array}{l} {t_{{\rm{f}}{j_1}{k_1}}} - {t_{{\rm{f}}{j_3}{k_2}}} \le - \frac{{{l_{{j_1},{j_2}}}}}{v}{t_{{\rm{f}}{j_1}{k_1}}} < {t_{{\rm{f}}{j_3}{k_2}}}\\ {t_{{\rm{f}}{j_1}{k_1}}} - {t_{{\rm{f}}{j_3}{k_2}}} \ge - \frac{{{l_{{j_3},{j_4}}}}}{v}{t_{{\rm{f}}{j_1}{k_1}}} \ge {t_{{\rm{f}}{j_3}{k_2}}} \end{array} \right. $ | (5) |
| $ {j_1} \in \left( {1,m} \right);{j_2} \in \left( {{j_1} + 1,m} \right) $ |
| $ {j_3} \in \left( {1,m} \right);{j_4} \in \left( {{j_3} + 1,m} \right) $ |
| $ {k_1},{k_2} \in \left( {1,n} \right);{k_1} \ne {k_2} $ |
最后一批工件在最后一个镀槽中加工结束的时间为所有工件的总加工时间,如式(6)所示。
| $ \begin{array}{*{20}{c}} {{g_1} = {t_{总\min }} = \cdots }\\ {\min \left( {{t_{s{n_1}}} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^n {\left( {r \cdot {\eta _{kj}} + {t_{kj}}} \right) + \frac{{{l_{1,m}}}}{v}} } } \right),} \end{array} $ | (6) |
式中:ηkj为tkj≠0时,ηkj=1,否则ηkj=0。
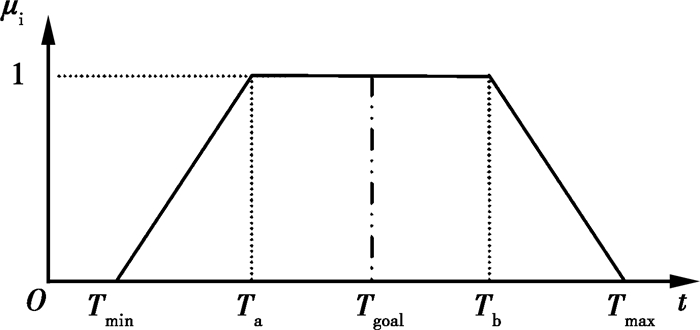
1.2.2 最小化拖期/提前惩罚对制造企业来讲,提前完工会增加库存成本,拖期会影响生产效率,实际生产中,提前/拖期对客户满意度影响符合梯形模糊隶属函数[14-15],如图 1所示。不同产品的重要性有一定差别,设(ə1,ə2…ən)为n批产品的重要因子,(μ1,μ2…μn)为n位客户满意度,最小化拖期/提前惩罚即使客户满意度与对应的重要因子之积最大,如公式(7)。
| $ {g_2} = \max \left( {\sum\limits_{i = 1}^n {{\partial _i}{\mu _i}} } \right) = \min \left( {\sum\limits_{i = 1}^n {\frac{1}{{{\partial _i}{\mu _i}}}} } \right)。$ | (7) |
|
图 1 交货期与客户满意度关系图 |
权衡最大完工时间和拖期/提前惩罚重要程度,设置加权函数:
| $ g = \min \left( {\alpha {g_1} + \beta {g_2}} \right), $ | (8) |
式中:α、β分别为最大完工时间和惩罚因素的加权系数。设E为g的估计最大值,将目标函数修改为式(9)。
| $ f = \max \left( {E - \left( {\alpha {g_1} + \beta {g_2}} \right)} \right)。$ | (9) |
自适应克隆竞争算法(ACCA)相对传统的克隆竞争算法来讲,具有较高的寻优能力,同时收敛速度快,算法描述如下:
Step1 初始化:产生2个初始种群A1、A2,各种群随机生产Pop_Size个抗体,对种群A1、A2 (以下用A代替)分别进行如下操作。
Step2 克隆:计算抗体亲和力,选择种群A中亲和力较高的m个抗体,按公式(10)进行克隆扩增操作,得到抗体群C;
| $ \begin{array}{*{20}{c}} {{P_c}\left( k \right) = \frac{{{P_{{\rm{cmax}}}} - {P_{{\rm{cmin}}}}}}{{{G_{\max }} - {G_{\min }}}}k + \cdots }\\ {\frac{{{G_{\max }} * {P_{{\rm{cmax}}}} - {P_{{\rm{cmin}}}} * {G_{\max }}}}{{{G_{\max }} - {G_{\min }}}},} \end{array} $ | (10) |
式中:Pcmax为最大克隆概率;Pcmin为最小克隆概率;Gmax为最大迭代次数;Gmin为最小迭代次数。
Step3 交叉变异:根据公式(11)对抗体群C进行交叉操作,得到抗体群D;
| $ \begin{array}{*{20}{c}} {{P_{\rm{h}}}\left( k \right) = \frac{{{P_{{\rm{hmax}}}} - {P_{{\rm{hmin}}}}}}{{{G_{\max }} - {G_{\min }}}}k + \cdots }\\ {\frac{{{G_{\max }} \cdot {P_{{\rm{hmax}}}} - {P_{{\rm{hmin}}}} \cdot {G_{\max }}}}{{{G_{\max }} - {G_{\min }}}},} \end{array} $ | (11) |
式中:Phmax为最大变异概率,Phmin为最小变异概率。
Step4 合并:合并抗体群A、D,去掉高浓度抗体,得抗体群E。
Step5 募集新成员:随机产生k个抗体,代替抗体群E中亲和力较低的k个抗体,得抗体群F。
Step6 竞争:将种群A1、A2进化获得的抗体群F1、F2相互竞争,选择最优抗体。
Step7:判断是否满足终止条件,若未终止,则交换A1、A2最优抗体,转至Step2。
3 仿真分析8批工件(P1~P8)在8个镀槽(M1~M2,M3.1~M3.3(并行工位)和M4~M6)中加工,行车带料移动速度v=1 m/s,相邻镀槽中心的距离l=1 m,行车取料、放料时间总和tr=3 s,行车数目h=1辆,最大完工时间加权系数α=0.3,惩罚因素加权系数β=0.7,各批工件的工艺参数即在各镀槽中的加工时间如表 1所示;产品信息参数,包括产品交货期t(单位为s)以及其重要因子ə(单位为1)如表 2所示。
| 表 1 产品工艺参数 |
| 表 2 产品信息参数 |
优化计算时,取总群大小Pop_Size=50,最大克隆概率Pcmax=0.8,最小克隆概率Pcmin=0.1,最大变异概率Phmax=0.8,最小变异概率Pnmin=0.1,使用计算机环境为Intel(R)Pentium(R)Dual T2390,Windows XP,1.86GHz,1G内存,用matlab仿真软件,分别采用传统克隆算法和自适应克隆竞争算法求解模型,各算法分分别进行20次实验,若不考虑惩罚因素,得最优排序方式为2->7->6->8->5->4->1->3,最小完工加工时间t总min=119 s,如图 2所示;同时考虑完工时间和惩罚因素,得目标函数最优解fbest=53.12,此时完工时间t总=138 s,最优排序为8->6->3->2->7->4->1->5,如图 3所示。

|
图 2 最小化最大加工时间调度甘特图 |

|
图 3 目标值最优解调度甘特图 |
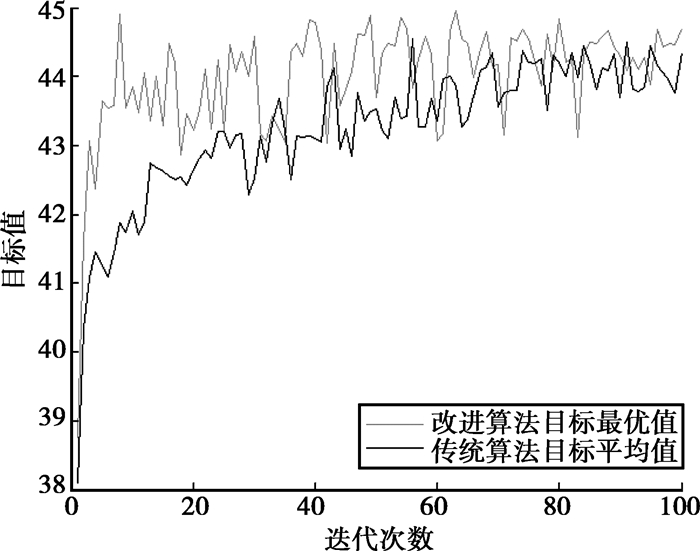
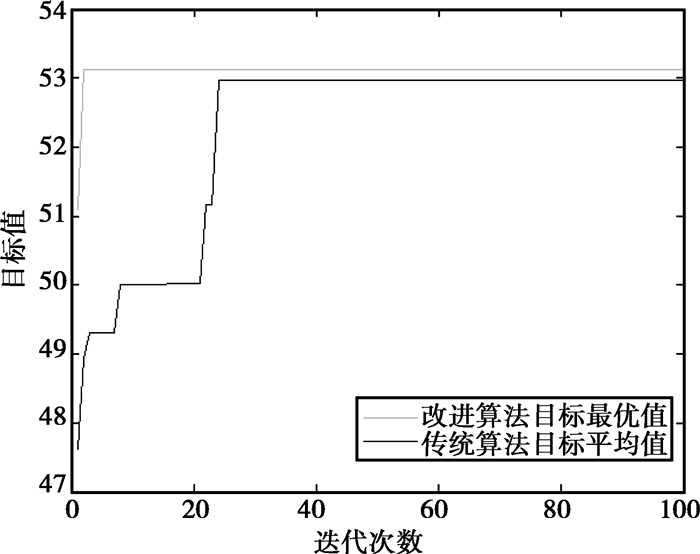
传统克隆算法和自适应克隆竞争算法性能对比见表 3、图 4和图 5。其中,Gmax为最大迭代次数,最小迭代次数Gmin=1,最小化最大完工时间与惩罚因素的加权函数最大估计值E=200,f、fbest、fwrost分别为目标值的平均值、最优值和最差值,S2为标准偏差,j*为寻优率。
| 表 3 ACCA和CSA性能对比 |
|
图 4 ACCA和CSA分别求解目标函数平均值 |
|
图 5 ACCA和CSA分别求解目标函数最优值 |
笔者从企业实际生产情况出发,针对带并行工位的自动化电镀生产线工件与行车的调度问题,提出了自适应克隆竞争算法(ACCA),有效地平衡了搜索全局最优值和局部最优值的能力,通过仿真实验证实,选择适当的参数,ACCA具有较高的收敛率和全局寻优能力,不仅有效地解决了该模型,同时对于多品种、小批量生产调度问题的求解以及对克隆算法的进一步研究具有参考价值。
| [1] |
刘爱军, 杨育, 邢青松, 等.
改进免疫克隆算法的Job Shop调度[J]. 重庆大学学报, 2011, 34(10): 61–67.
LIU Aijun, YANG Yu, XING Qingsong, et al. Job-shop scheduling based on improved immune cloning algorithm[J]. Journal of Chongqing University, 2011, 34(10): 61–67. (in Chinese) |
| [2] | Zhang R, Wu C. A hybrid immune simulated annealing algorithm for the job shop scheduling problem[J]. Applied Soft Computing, 2010, 10(1): 79–89. DOI:10.1016/j.asoc.2009.06.008 |
| [3] | Eswaramurthy V P, Tamilarasi A. Tabu search strategies for solving job shop scheduling problems[J]. Journal of Advanced Manufacturing Systems, 2007, 6(1): 59–75. DOI:10.1142/S0219686707000899 |
| [4] | Zhang C Y, Rao Y Q, Li P G. An effective hybrid genetic algorithm for the job shop scheduling problem[J]. The International Journal of Advanced Manufacturing Technology, 2008, 39(9/10): 965–974. |
| [5] |
郑忠, 朱道飞, 高小强.
钢厂炼钢-连铸生产调度及重计划方法[J]. 重庆大学学报, 2008, 31(7): 820–824.
ZHENG Zhong, ZHU Daofei, GAO Xiaoqing. An approach of production scheduling and replanning in a steelmaking-continuous casting plant[J]. Journal of Chongqing University, 2008, 31(7): 820–824. DOI:10.11835/j.issn.1000-582X.2008.07.023 (in Chinese) |
| [6] | Bagheri A, Zandieh M, Mahdavi I, et al. An artificial immune algorithm for the flexible job-shop scheduling problem[J]. Future Generation Computer Systems, 2010, 26(4): 533–541. DOI:10.1016/j.future.2009.10.004 |
| [7] | Luh G C, Chueh C H. A multi-modal immune algorithm for the job-shop scheduling problem[J]. Information Sciences, 2009, 179(10): 1516–1532. DOI:10.1016/j.ins.2008.11.029 |
| [8] |
魏圆圆, 唐超礼, 黄友锐.
自适应克隆选择算法及其仿真研究[J]. 模式识别与人工智能, 2009, 22(2): 202–207.
WEI Yuanyuan, TANG Chaoli, HUANG Yourui. Adaptive clonal selection algorithm and its simulation[J]. Pattern Recognition and Artificial Intelligence, 2009, 22(2): 202–207. (in Chinese) |
| [9] |
李敏强, 寇纪淞.
多模态函数优化的协同多群体遗传算法[J]. 自动化学报, 2002, 28(4): 497–504.
LI Minqiang, KOU Jisong. Coordinate multi-population genetic algorithms for multi-modal function optimization[J]. Acta Automatica Sinica, 2002, 28(4): 497–504. (in Chinese) |
| [10] | Castro L N D, Zuben F J V. Learning and optimization using the clonal selection principle[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(3): 239–251. DOI:10.1109/TEVC.2002.1011539 |
| [11] | Castro L N D, Zuben F J V. The clonal selection algorithm with engineering applications[EB/OL].[2011-11-17]. http://wenku.baidu.com/view/ed1f630e76c66137ee0619e8.html. |
| [12] | 杨志才. 化工生产中的间歇过程[M]. 北京: 化学工业出版社, 2001. |
| [13] |
田志锋, 尚宏利, 姚威.
自动化集成电镀生产线的生产调度问题[J]. 重庆理工大学学报:自然科学, 2011, 25(6): 38–44.
TIAN Zhifeng, SANG Hongli, YAO Wei. Schedule problem for automatic integrated electroplated product lines[J]. Journal of Chongqing University Institute of Technology:Natural Science, 2011, 25(6): 38–44. (in Chinese) |
| [14] |
李富明, 朱云龙, 尹朝万, 等.
可变机器约束的模糊作业车间调度问题研究[J]. 计算机集成制造系统, 2006, 12(2): 169–173, 197.
LI Fuming, ZHU Yunlong, YIN Chaowan, et al. Research on fuzzy job shop scheduling with alternative machines[J]. Computer Integrated Manufacturing Systems, 2006, 12(2): 169–173, 197. (in Chinese) |
| [15] |
刘爱军, 杨育, 邢青松, 等.
多目标模糊柔性车间调度中的多种群遗传算法[J]. 计算机集成制造系统, 2011, 17(9): 1954–1961.
LIU Aijun, YANG Yu, XING Qingsong, et al. Multi-population genetic algorithm in multiobjective fuzzy and flexible job shop scheduling[J]. Computer Integrated Manufacturing Systems, 2011, 17(9): 1954–1961. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

