2. 湖北工业大学, 武汉 430068;
3. 中船重工环境工程有限公司, 武汉 430064
2. Hubei University of Technology, Wuhan 430068, China;
3. CSIC Environmental Engineering Co. Ltd., Wuhan 430064, China
循环冷却水系统在化工、电力、冶金等工业生产系统中是不可分割的一部分,循环冷却水系统的正常运行是整套生产系统正常运行的重要保障。冷却水在循环系统中不断循环使用,因水温升高、流速变化、水蒸发、各种无机离子和有机物质浓缩,pH值升高,冷却塔等在室外受到阳光照射、风吹雨淋、灰尘杂质进入,以及设备结构和管道材质等多种因素的综合作用,会产生比直流系统更为严重的水垢污垢附着、设备腐蚀和微生物孽生等问题[1-2],直接影响到其安全、稳定、经济运行。目前国内外解决循环冷却水系统的这三大问题常见的方法为添加化学药剂[3]。在化学加药处理中,pH值是一个非常重要的影响因素,它同循环水系统换热设备表面的结垢和腐蚀密切相关[4]:循环水pH值过高,系统结垢倾向增大;pH值过低,系统腐蚀趋势增大[5]。在循环冷却水系统中,阻垢剂、缓蚀剂等水质稳定剂的添加及其使用效果也与pH值有很大的联系[6]。目前,国内外鲜少有报道对循环冷却水pH值变化情况进行理论系统分析,对循环冷却水pH值的研究主要集中在pH值与总碱度的热力学关系[5, 7]与材料的腐蚀上[8-9],也有少数研究不同pH值水流的混合与碱度的关系[10]。
鉴于此,笔者提出了循环冷却水pH值的准动态变化数学模型,并进行了试验验证,在验证试验的基础上,计算了CO2气体在循环冷却水与空气中的气液传质系数,以进一步为循环冷却水pH值动态变化数学模型的建立与实时预测提供理论基础和试验依据,实现对循环水运行工况的在线连续监控。
1 理论计算与数学建模 1.1 循环水碳酸盐平衡计算循环冷却水系统在运行过程中,随着换热的进行,水温不断升高,导致循环冷却水与空气之间产生温差。在循环冷却水不断被蒸发、浓缩过程中,空气中CO2气体与循环水充分接触,在未达到气液两相平衡之前,气膜侧与气液两相界面CO2存在浓度差,随着空气的气提作用,循环水中的CO2从水中逸出,直至达气液两相平衡[11]。在循环冷却水气液两相传质过程中,循环水pH值不断上升。
在循环水中,影响水溶液pH值的介质主要为碳酸盐(HCO3-和CO32-)。当碳酸盐与空气中的CO2充分接触后,达到气液两相平衡,水中的pH值受大气中二氧化碳浓度的控制[12],其pH值则稳定在平衡pH值上。
循环水平衡后的总碱度B,表达式为[13]
| $ B = 2 \cdot \left[ {{\rm{CO}}_3^{2 - }} \right] + \left[ {{\rm{HCO}}_3^ - } \right] + \left[ {{\rm{O}}{{\rm{H}}^ - }} \right]。$ | (1) |
利用空气CO2气体在循环水中的溶解平衡及碳酸的一级和二级电离平衡关系式,可得在达气液两相平衡时,循环水平衡pH值与总碱度B的关系为[14]
| $ \begin{array}{*{20}{c}} {{\rm{PH}} = }\\ { - \log \frac{{\left( {{K_{\rm{w}}} + A} \right) + \sqrt {{{\left( {{K_{\rm{w}}} + A} \right)}^2} + 8 \cdot B \cdot {P_{{\rm{C}}{{\rm{O}}_2}}} \cdot A} }}{{2 \cdot B}},} \end{array} $ | (2) |
| $ A = \left( {{P_{{\rm{C}}{{\rm{O}}_2}}} \cdot H \cdot {K_1}} \right)。$ | (3) |
碳酸盐溶液的平衡pH值受温度影响较大,随着温度的变化,溶液的平衡常数发生变化。因此,温度会影响到水的pH值。温度T对平衡常数K的影响,遵循Vant Hoff公式(如公式(4)所示),故由Vant Hoff公式可得出不同温度下碳酸盐溶液的理论平衡pH值[15]。
| $ \ln K = \ln {K_0} + \frac{{\Delta {H^0}}}{R} \cdot \left( {\frac{1}{{{T_0}}} - \frac{1}{T}} \right)。$ | (4) |
不同温度下,循环水分别在15℃、25℃和40℃下的平衡pH值如图 1所示。

|
图 1 不同温度下碳酸盐溶液的理论平衡pH值 |
由图 1可知:碳酸盐溶液的平衡pH值随温度和碱度的升高而增加,在碱度低于2.0×10-2 mol/L时,溶液的平衡pH值随碱度的升高而大幅度提高;在碱度高于2.0×10-2 mol/L时,其平衡pH值的提高缓慢,最后趋近于10.0。因此,在特定的循环冷却水系统中,碳酸盐溶液的平衡pH值与其温度无关。
1.2 循环水准动态pH值数学建模以气体在气液两相传质的双膜理论为基础,构建循环水系统准动态pH值变化动力学模型。循环冷却水系统模拟准动态运行流程如图 2所示:循环泵一方面将部分循环水进行循环,起充分混合作用,另一方面将另一部分循环水进行喷淋、脱气,以模拟循环水在气液两相的传质过程。

|
图 2 循环冷却水准动态试验系统示意图 |
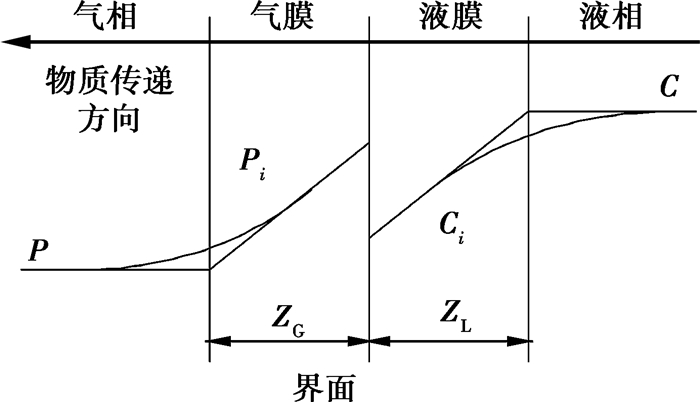
同时系统会补水以及浓水排放,以维持系统一定的浓缩倍率。在碳酸盐体系气液两相传质过程中,当空气中的气体分压低于气液两相界面的气体分压时,气体传质方向由溶液侧向气体侧扩散,其双膜理论示意图如图 3所示。
|
图 3 CO2气体在气液两相中的传质示意图 |
基于气液两相双膜理论,对循环水pH值进行实时预测理论分析,建立碳酸盐体系pH值与时间t的数学关系。
根据CO2气体在气液两相传质的双膜理论,CO2物料守恒定律及循环水平衡pH值与总碱度B的关系式,可构建循环水pH值准动态变化的数学模型,数学模型如公式(5)所示:
| $ \begin{array}{*{20}{c}} {t = - \frac{V}{Q} \cdot \left[ {\ln \left( {1 - \frac{{\left( {C - D} \right) \cdot Q}}{{\left( {\frac{{C \cdot E}}{{{C_{{{\rm{H}}_2}{\rm{O}}}}}} - {P_{{\rm{C}}{{\rm{O}}_2}}}} \right) \cdot A \cdot {K_G}}}} \right)} \right],}\\ {C = \frac{{B - \frac{{{K_{\rm{W}}}}}{{{C_{{\rm{H}}_0^ + }}}}}}{{\frac{{2 \cdot {K_1} \cdot {K_2}}}{{C_{{\rm{H}}_0^ + }^2}} + \frac{{{K_{\rm{1}}}}}{{{C_{{\rm{H}}_0^ + }}}}}};D = \frac{{B - \frac{{{K_{\rm{W}}}}}{{{C_{{{\rm{H}}^ + }}}}}}}{{\frac{{2 \cdot {K_1} \cdot {K_2}}}{{C_{{\rm{H}}_0^ + }^2}} + \frac{{{K_{\rm{1}}}}}{{{C_{{{\rm{H}}^ + }}}}}}}。} \end{array} $ | (5) |
公式(5)可转化为公式(6):
| $ D = C + A \cdot {K_{\rm{G}}} \cdot \frac{1}{Q}\left( {{P_{{\rm{C}}{{\rm{O}}_2}\left( {空} \right)}} - \frac{{E \cdot C}}{{{C_{{{\rm{H}}_2}{\rm{O}}}}}}} \right) \cdot \left( {1 - {{\rm{e}}^{ - \frac{Q}{V} \cdot t}}} \right)。$ | (6) |
当曝气时间t趋于无穷大时,式子(6)可简化成式子(7):
| $ D = C + A \cdot {K_{\rm{G}}} \cdot \frac{1}{Q}\left( {{P_{{\rm{C}}{{\rm{O}}_2}\left( {空} \right)}} - \frac{{E \cdot C}}{{{C_{{{\rm{H}}_2}{\rm{O}}}}}}} \right)。$ | (7) |
因此循环水系统CO2气体的传质系数KG可通过公式(7)求得。
| $ A \cdot {K_{\rm{G}}} = \frac{{Q \cdot \left( {D - C} \right)}}{{\left( {{P_{{\rm{C}}{{\rm{O}}_2}\left( {空} \right)}} - \frac{{E \cdot C}}{{{C_{{{\rm{H}}_2}{\rm{O}}}}}}} \right)}}, $ | (8) |
式中:A为气液相接触面积,m2;B为循环水甲基橙碱度,mol/L;C为循环水初始H2CO3浓度,mol/L;D为循环水H2CO3浓度,mol/L;E为CO2亨利系数,Pa;K1、K2分别为H2CO3一、二级电离常数;PCO2(空)为空气中CO2气体分压,32 Pa;V为循环水容量,L;Q为喷淋流量,L/h。
本试验的气液传质过程采用微孔喷淋的方式进行,喷淋液柱高度H为1.28 m,喷淋孔口直径d为1 mm,微孔数目n为100。在一定曝气强度下,气液相接触面积A=nπdH=1.0×10-3 m2。
不同循环流量下A·KG的计算值和KG值如表 1所示;在碱度为3.10×10-3 mol/L的循环水中CO2气体的传质系数与喷淋流量的关系如图 4所示。
| 表 1 不同喷淋量与碱度下CO2气体传质系数 |
|
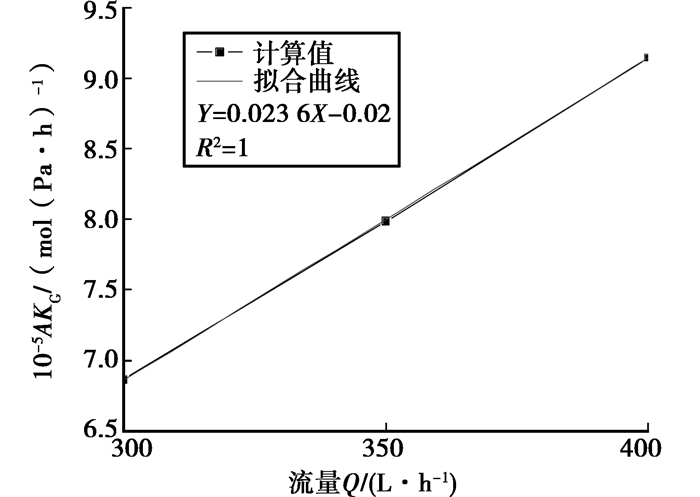
图 4 CO2气体传质系数与喷淋流量关系 |
表 1表明:在系统初始喷淋流量、循环温度为定值时,A·KG值不会随碱度的变化而改变,其值在9.42×10-5~9.42×10-5 mol/(Pa·h)之间。由在40℃下,喷淋流量300,350与400 L/h的计算结果表明喷淋流量与A·KG值呈线性关系,线性相关度为1。A·KG值与流量Q的关系为
| $ {10^5}A \cdot {K_{\rm{G}}} = 0.0236Q - 0.02。$ | (9) |
当喷淋流量为400 L/h时,试验系统KG值为9.42×10-2 mol/(m2·Pa·h);喷淋流量为350 L/h时,试验系统KG值为8.24×10-2 mol/(m2·Pa·h);喷淋流量为300 L/h时,试验系统KG值为7.06×10-2 mol/(m2·Pa·h),不受初始循环水pH值、碱度的影响。
2 试验方法 2.1 碳酸盐体系平衡测试配制不同碱度(2.0~22.0×10-3 mol/L)的碳酸氢钠溶液,将溶液加热至40℃,并通过鼓风机进行曝气,并不断监测碳酸盐溶液pH值,直至pH值趋于稳定为止。研究曝气过程中,碳酸盐溶液的气液两相平衡状态。曝气后,碳酸盐溶液的稳定pH值与其平衡pH值对比,确定曝气过程中碳酸盐溶液的平衡状态。
2.2 循环水准动态pH值测试建立循环水准动态pH值测试系统,如图 2所示,以研究在不同循环水初始pH值、初始碱度以及喷淋流量等变化因素下,循环水pH值随时间的变化曲线。循环水系统的测试参数见表 2。
| 表 2 循环水准动态实验测试参数 |
40℃不同碱度的碳酸盐溶液在曝气后,pH值达到稳定状态[16],测定结果如图 5所示。
|
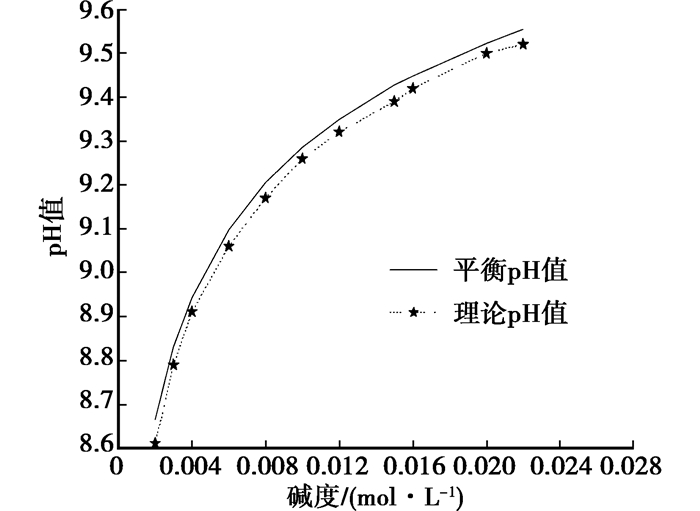
图 5 碳酸盐溶液平衡pH值与测定pH值的比较(40℃) |
图 5结果表明,曝气后,碳酸盐溶液的稳定pH值与其平衡pH值的误差在0.04之内。因此,在误差范围内,表明该循环水动态曝气准动态变化模型是可靠的,同时进一步证明在充分曝气后的循环冷却水pH值近似于平衡pH值。可用此模型对循环水动态曝气过程进行模拟。
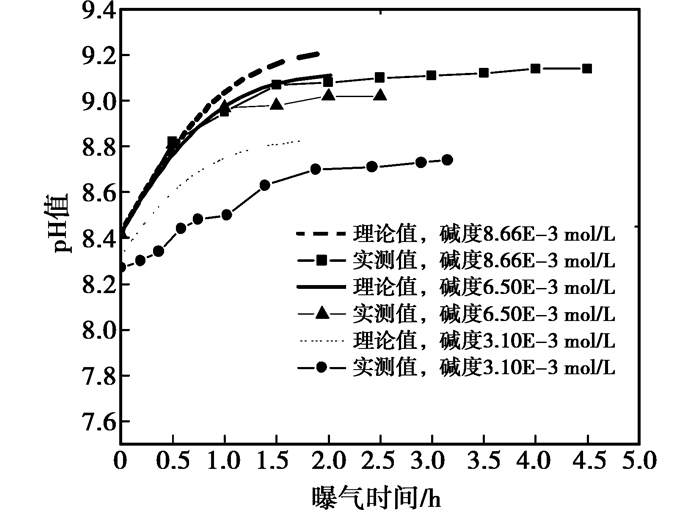
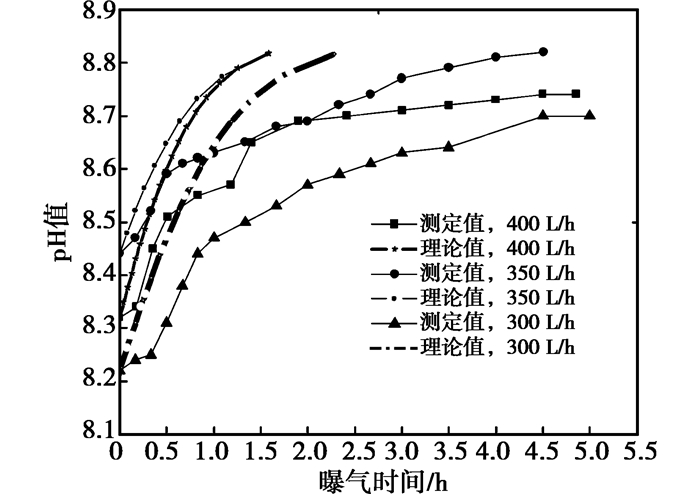
3.2 循环冷却水准动态pH值测试图 6为在喷淋流量400 L/h下不同碱度循环水在CO2气体传质过程中的pH值变化曲线;图 7为不同喷淋流量下3.10×10-3 mol/L碱度的循环水在CO2气体传质过程中的pH值变化曲线图。
|
图 6 循环水准动态系统的在不同碱度下平衡pH值与测定pH值变化趋势(Q=400 L/h) |
|
图 7 碱度为3.10×10-3 mol/L的碳酸盐在不同流量下的pH值变化 |
图 6结果表明:不同碱度的循环水的实测pH值变化趋势与理论pH值变化相同。当在喷淋流量为400 L/h时,循环水在均在2 h内达到气液两相平衡状态,实测pH与理论pH值之差值小于0.1。比较图 7中各流量下的实测pH值与理论pH值变化得出:碱度3.10×10-3 mol/L的循环水在不同喷淋流量下,其实测pH值变化趋势与理论pH变化相同。实际测定结果与理论计算有较好的吻合度。因此,推导出的数学理论模型可用于指导循环水准动态系统的pH值预测及CO2气体传质系数的计算。
4 结论通过采用循环水准动态模拟试验对碳酸盐体系的平衡状态及CO2气体的两相传质过程进行试验研究和理论分析,可以得到以下结论:
1) 碳酸盐体系与空气中的CO2发生充分传质过程,体系pH值达到稳定后,测量pH值与理论平衡值最大误差为0.04。因此,认为碳酸盐体系在循环水系统中,经过充分的传质过程已达到平衡状态。
2) CO2气体在循环水系统中的理论传质系数KG为当Q与A固定时,可通过计算模型进行计算,实验条件下,40℃时,A·KG值与流量Q的关系为:105·A·KG=0.023 6Q-0.02。同时,通过循环水准动态试验测试并验证循环水准动态系统pH值,其变化趋势与理论计算相一致。因此,理论推导出的循环水准动态pH值与运行时间t的数学关系与试验结果,可为循环冷却水动态pH值变化趋势的预测提供理论和试验基础。
| [1] | Touir R, Dkhireche N, Touhami M E, et al. Corrosion and scale processes and their inhibition in simulated cooling water systems by monosaccharides derivatives:part Ⅰ:EIS study[J]. Desalination, 2009, 249(3): 922–928. DOI:10.1016/j.desal.2009.06.068 |
| [2] |
黄娟, 徐强, 任志峰, 等.
循环冷却水缓蚀剂和阻垢剂的研究进展[J]. 电镀与精饰, 2009, 31(2): 22–25, 31.
HUANG Juan, XU Qiang, REN Zhifeng. Research progress of corrosion and scale inhibitors in circulating cooling water[J]. Plating and Finishing, 2009, 31(2): 22–25, 31. (in Chinese) |
| [3] | Sun M J, Lei Y, Xi L J, et al. Cooling water screening test of corrosion and scale inhibitors[J]. Material Science Forum, 2011, 694: 794–798. DOI:10.4028/www.scientific.net/MSF.694 |
| [4] |
王世兴.
pH-碱度关系在循环冷却水中的应用[J]. 内蒙古石油化工, 2011(14): 31–32.
WANG Shixing. The application of the relationship between pH and alkalinity in circulating cooling water[J]. Inner Mongulia Petrochemical Industry, 2011(14): 31–32. DOI:10.3969/j.issn.1006-7981.2011.14.012 (in Chinese) |
| [5] |
李贺全, 王应高, 李永立.
循环冷却水pH-碱度的理论计算和分析[J]. 工业水处理, 2008, 28(12): 22–24.
LI Hequan, WANG Yinggao, LI Yongli. Theoretical calculation and analysis of the pH-alkalinity of circulating cooling water[J]. Industrial Water Treatment, 2008, 28(12): 22–24. DOI:10.3969/j.issn.1005-829X.2008.12.006 (in Chinese) |
| [6] | Spicka K J, Johnston C J, Jordan M M, et al. The impact of organic acid on scale inhibitor/corrosion inhibitor interaction, a case study from West Africa[C]//Proceedings of the SPE International Symposium on Oilfield Chemistry, April 11-13, 2011, The Woodlands, Texas, USA.[S.l.]:Society of Petroleum Engineers, 2011, 1:310-317. |
| [7] |
王锋涛, 王玉秀.
循环冷却水水质pH与碱度关系的试验研究[J]. 工业水处理, 2010, 30(11): 75–76.
WANG Fengtao, WANG Yuxiu. Test and research on the relationship between the pH and the alkalinity[J]. Industrial Water Treatment, 2010, 30(11): 75–76. DOI:10.11894/1005-829x.2010.30(11).75 (in Chinese) |
| [8] | Cheng X Q, Lv S J, Liu Z J, et al. The influence of pH values on corrosion properties of 316L stainless steel in simulated circulating cooling water[J]. Advanced Materials Research, 2011, 152/153: 1103–1106. |
| [9] | Deyab M A. The influence of different variables on the electrochemical behavior of mild steel in circulating cooling water containing aggressive anionic species[J]. Journal of Solid State Electrochemistry, 2009, 13(10): 1737–1742. |
| [10] | Dabrowski W, Buchta R, Mackie R I. Impact of water blending on calcium carbonate equilibrium in water distribution systems[J]. Journal of Environmental Engineering, 2004, 130(9): 1059–1062. DOI:10.1061/(ASCE)0733-9372(2004)130:9(1059) |
| [11] | Jani J M, Aran H C, Wessling M, et al. Modeling of gas-liquid reactions in porous membrane microreactors[J]. Journal of Membrane Science, 2012, 419/420: 57–64. DOI:10.1016/j.memsci.2012.06.044 |
| [12] | Montety V D, Martin J B, Cohen M J, et al. Influence of diel biogeochemical cycles on carbonate equilibrium in a karst river[J]. Chemical Geology, 2011, 283(1/2): 31–43. |
| [13] | 许保玖. 给水处理理论[M]. 北京: 中国建筑工业出版社, 2000. |
| [14] | Lin J Y, Ye C S, Zeng H M, et al. Nanofiltretion and ion-exchange alkalinization for water conservation and zerodischarge in circulating cooling water system[C]//Proceedings of the 2009 Asia-Pacific Power and Energy Engineering Conference, March 27-31, 2009, Wuhan, China. Piscataway:IEEE Press, 2009:1-4. |
| [15] | 陈绍炎. 水化学[M]. 北京: 水利电力出版社, 1989. |
| [16] | Ye C S, Lin J Y, Yang H, et al. Ion exchange equilibrium carbonate treatment for anticorrosion in open recirculating cooling water system[J]. Industrial and Engineering Chemistry Research, 2010, 49(20): 9625–9630. DOI:10.1021/ie100913d |
 2013, Vol. 36
2013, Vol. 36

