汽车转向机构是实现汽车行驶过程中及时、准确转向或保持直线行驶的机构,它通过合理分配汽车左、右车轮的转角关系促使车轮按预期的轨迹运动,以保证汽车的正常行驶。目前,国内外学者对转向机构的分析与综合开展了较为广泛的研究。较为典型的有,Wolfe[1]在1959年提出了平面四杆Ackerman转向机构的解析综合方法;Yao和Angeles[2]运用计算运动学方法来进行转向机构综合;Simionescu和Beale[3]较为系统地研究了平面四杆Ackerman转向机构的优化综合问题;Bian和Song等[4]将汽车悬架和转向机构考虑成一个整体来进行优化综合,并考虑了轮胎的弹性对机构运动误差的影响;Lin等[5]对重载汽车转向机构的几种优化综合方法进行比较研究。上述研究为提高汽车转向机构的运动精度提供了非常有效的设计方法,但均局限于确定性参数范畴内。
然而真实机构系统总是存在着不确定性,如几何尺寸随机性、运动副间隙、受力受热变形、磨损等。这些不确定性会导致机构运动输出的不确定性,进而引起机构的运动精度失效[6]、动作不可靠、运动不协调等。概率统计方法已成为处理这类问题的重要方法。就汽车转向机构而言,文献[7]中对齿轮齿条式转向机构的可靠性灵敏度进行了相关分析,文献[8-9]中利用FOSM方法建立了考虑尺寸变量的不确定性影响下的转向机构运动精度模型并在此基础上建立了机构可靠性灵敏度模型,文献[10]研究尺寸变量不确定性和运动副间隙共同作用下的转向机构运动精度可靠性及可靠性灵敏度。此外,文献[11]在考虑可控因素的前提下,建立了转向机构基于区间的非概率可靠性优化模型,并与传统的可靠性优化方法进行比较分析。
上述研究大多局限于机构在其运动范围内某特定点的可靠度问题或称为点可靠度问题,它是瞬时的、局部的和静态的。从机构精度理论角度看,点可靠度能够很好地评定机构在某一位置上的运动精度,能够确定机构在哪些位置的运动精度是高还是低。但它不能用以评定机构在整个期望运动行程上的运动精度,不能确定机构在整个运动行程上实现期望预定规律的精度的高低。而从机构运动精度可靠度定义可以看出,机构运动可靠度既有研究某特定点可靠度的问题也包含在整个运动时间历程内整个运动区间上的可靠度问题。后者被称为机构运动的时变可靠度[12-13]。目前,仅有少数学者就机构运动时变可靠度进行了相关研究[14-16],但这些研究成果用于机构的分析与综合还具有一定的距离。最近,Zhang和Du[12-13]就机构运动时变可靠性进行了较为深入的研究,他们采用一次二阶矩方法结合首次穿越理论推导了求解函数生成机构的时变可靠度的穿越率解析公式,在此基础上研究了函数生成机构运动不确定性的概率分析与综合。为此,笔者基于文献[12]所提出的时变可靠性求解策略和算法研究整体式转向机构的时变可靠性分析与综合,提出一种考虑不确定性因素影响下高精度真实转向机构的设计方法。
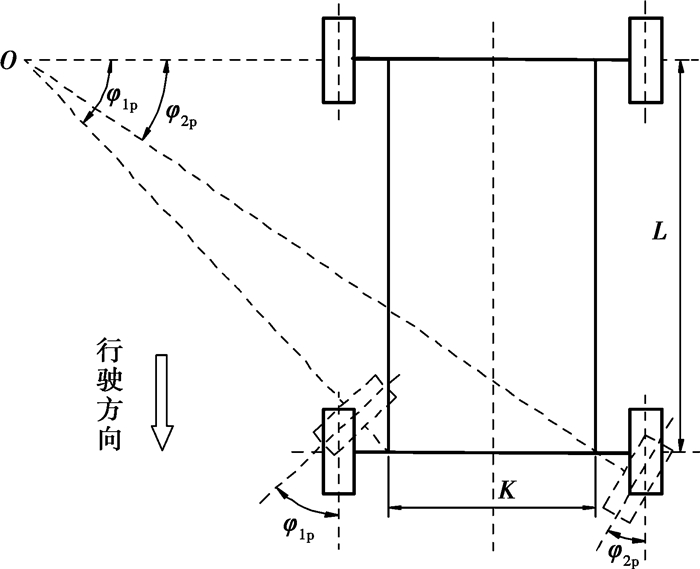
1 转向机构运动分析 1.1 阿克曼转向原理汽车转向机构是实现汽车行驶过程中及时、准确转向或保持直线行驶的机构。众所周知,在汽车转向行驶时,为避免过多的附加阻力、功率消耗以及轮胎的过度磨损等现象,必须实现汽车无侧滑(做纯滚动)现象,即使两侧车轮的转角满足阿克曼(Ackerman)转向原理。如图 1所示,轮式车辆转向时所有车轮都必须围绕同一瞬心O相对于地面转动,以保证所有车轮均作纯滚动。由图 1几何关系可得到阿克曼转向方程为
| $ \cot {\varphi _{2{\rm{p}}}} - \cot {\varphi _{1{\rm{p}}}} = \frac{K}{L}, $ | (1) |
|
图 1 阿克曼转向原理 |
式中:K为两侧主销轴线与地面相交点之间的距离;L为汽车轴距;φ2p为理想外侧车轮转角;φ1p为理想内侧车轮转角。
式(1)通常被称为汽车转向的理想关系式,真实机构是不可能精确实现的,总存在一定的误差。若以φ1p为输入转向角,φ2p为输出转向角,令ρ=L/K,则式(1)可写成
| $ {\varphi _{2{\rm{p}}}} = {\rm{arccot}}\left( {\frac{1}{\rho } + \cot {\varphi _{1{\rm{p}}}}} \right)。$ | (2) |
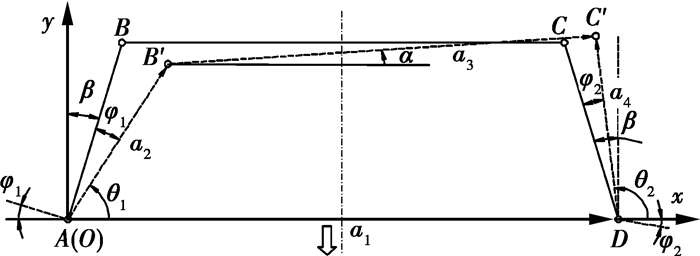
真实情况下,转向机构为复杂的空间机构,通常在许可范围内将转向机构简化为平面连杆机构进行研究。图 2为简化后的后置整体式平面四杆转向机构简图,由于其结构简单、动作可靠、精度较高、价格便宜等优点,使其广泛应用于轮式车辆(包含常用汽车、轮式拖拉机、农用车等)的转向系统中。整体式转向机构主要由转向摇臂、转向直拉杆、转向节臂、转向横拉杆和左右梯形臂组成。图中,β为梯形臂底角(初始角);AD为主销间距,其长度为a1;BC为转向横拉杆, 其长度为a3;AB、CD分别为左、右梯形臂,其长度分别为a2和a4。
|
图 2 整体式转向机构简图 |
图 2中,虚线表示转向机构梯形臂AB向右转过角度φ1时梯形臂CD转过φ2时刻转向机构位置矢量图。定义φ1为该转向机构运动输入角,φ2为运动输出角,θ1、α和θ2分别为杆矢量a2、a3和a4的方位角,规定其逆时针为正。根据图 2,整体转向机构的运动方程可表示为
| $ \left\{ \begin{array}{l} {a_2}\cos {\theta _1} + {a_3}\cos \alpha - {a_1} - {a_4} \cdot \cos {\theta _2} = 0,\\ {a_2}\sin {\theta _1} + {a_3}\sin \alpha - {a_4}\sin {\theta _2} = 0。\end{array} \right. $ | (3) |
进一步化简式(3)得到
| $ {k_1} + {k_2}\cos {\theta _2} - {k_3}\cos {\theta _1} - {k_4}\cos \left( {{\theta _1} - {\theta _2}} \right) = 0, $ | (4) |
式中:k1=a12+a22-a32+a42;k2=2a1a4;k3=2a1a2;k4=2a2a4。
根据式(4)可得到
| $ {\theta _2} = 2\arctan \left( {\frac{{A - \sqrt {{A^2} + {B^2} - {C^2}} }}{{B + C}}} \right), $ | (5) |
式中:A=-k4sin θ1;B=k2-k4cos θ1;C=k3cos θ1-k1。
由图 2,θ1与转向角φ1的关系为
| $ {\varphi _2}\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) = \frac{{\rm{ \mathsf{ π} }}}{2} + \beta - {\theta _2}, $ | (6) |
式中X=(a1, a2, a3, a4)。
1.3 转向机构运动误差以图 2所示机构右转为例,定义实际机构运动输入转向角为φ1、输出转向角为φ2,并规定理想输入转向角φ1p=φ1,那么实际输出转向角φ2与理想输出转向角φ2p之间的误差可以表示为
| $ g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) = {\varphi _2}\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) - {\varphi _{2p}}\left( {{\varphi _1}} \right), $ | (7) |
式中,X=(a1, a2, a3, a4)为机构构件尺寸随机变量。
通常,构件尺寸X可看作服从正态分布且相互独立的随机变量,即X~N(μX, σX)。其中μX=(μ1, μ2, …, μn)为随机变量X的均值;σX=(σ1, σ2, …, σn)为随机变量X的标准差。因为机构构件尺寸公差相对于构件名义尺寸很小,故尺寸变量的标准差σX相对于均值μX也很小。因此用误差函数g(X, φ1)在均值μX处的线性近似函数代替原误差函数g(X, φ1)具有足够的精度[15-17]。将误差函数g(X, φ1)在均值μX处进行一阶泰勒展开得到
| $ \begin{array}{l} g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) \approx \hat g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) = g\left( {{\mu _X},{\varphi _1}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {\frac{{\partial g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right)}}{{\partial {\mathit{\boldsymbol{X}}_i}}}} \left| {_{{\mu _X}}} \right. \cdot \left( {{\mathit{\boldsymbol{X}}_i} - {\mu _i}} \right)。\end{array} $ | (8) |
由于尺寸变量X呈正态分布,故可将尺寸变量X作如下变换
| $ {\mathit{\boldsymbol{X}}_i} = {\mu _i} + {\sigma _i}\mathit{\boldsymbol{U}}, $ | (9) |
式中U为标准正态分布,即Ui~N(0, 1)。
于是线性函数ĝ(X, φ1)可写为
| $ \hat g\left( {\mathit{\boldsymbol{U}},{\varphi _1}} \right) = {b_0}\left( {{\varphi _1}} \right) + \sum\limits_{i = 1}^n {{b_i}\left( {{\varphi _1}} \right){U_i}} , $ | (10) |
式中:U=(U1, U2, …, Un);b0(φ1)=g(μX, φ1);
由式(10)可以看出,机构的运动误差由结构误差和随机误差两部分组成。式中b0(φ1)为机构结构误差,
| $ {\mu _g}\left( {{\varphi _1}} \right) = {b_0}\left( {{\varphi _1}} \right) = \left( {{\varphi _2}\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) - {\varphi _{2{\rm{p}}}}\left( {{\varphi _1}} \right)} \right)\left| {_{{\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{X}}}}} \right.。$ | (11) |
现采用直接线性化方法[16]对式(3)求解可得到bi(φ1),即
| $ \mathit{\boldsymbol{b}}\left( {{\varphi _1}} \right) = \frac{{ - {\mathit{\boldsymbol{H}}^{\rm{T}}}}}{T} \cdot {\mathit{\boldsymbol{\sigma }}_\mathit{\boldsymbol{X}}}, $ | (12) |
其中,H和T分别为
| $ \mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {2{a_1} + 2{a_4}\cos {\theta _2} - 2{a_2}\cos {\theta _1}}\\ {2{a_2} - 2{a_1}\cos {\theta _1} - 2{a_4}\cos \left( {{\theta _1} - {\theta _2}} \right)}\\ { - 2{a_3}}\\ {2{a_4} + 2{a_1}\cos {\theta _2} - 2{a_2}\cos \left( {{\theta _1} - {\theta _2}} \right)} \end{array}} \right], $ | (13) |
| $ T = 2{a_1}{a_4}\sin {\theta _2} + 2{a_2}{a_4}\sin \left( {{\theta _1} - {\theta _2}} \right), $ | (14) |
式中:b(φ1)=(b1(φ1), b2(φ1), b3(φ1), b4(φ1));σX=(σ1, σ2, σ3, σ4)。
根据ĝ(X, θ)服从正态分布可导出转向机构运动输出误差的标准差σg(φ1)为
| $ {\sigma _g}\left( {{\varphi _1}} \right) = {\left[ {\sum\limits_{i = 1}^n {b_{\rm{i}}^2\left( {{\varphi _1}} \right)} } \right]^{0.5}}。$ | (15) |
从式(11)和(15)可知,机构运动输出误差的均值和标准差均为时间的函数且其均值不为零,因此机构运动输出误差为非平稳高斯过程[12-13]。
2 转向机构运动可靠性分析机构运动精度可靠度定义为在给定运动区间上机构运动的实际输出(如输出点位置、姿态)满足期望运动输出的概率,或者定义为机构运动输出误差位于允许误差范围内的概率[18]。该定义包含了两个层面的含义,一是机构在给定运动区间上某点处的可靠度,二是机构在整个给定运动区间上的可靠度。前者称其为点可靠度,后者则用时变可靠度描述。
2.1 机构运动点可靠性根据式(7),转向机构在其运动范围内φ1处的运动精度可靠度为
| $ \begin{array}{l} R = \Pr \left\{ {\left| {g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right)} \right| \le \varepsilon } \right\} = \\ \;\;\;\;\;\;\Pr \left\{ { - \varepsilon \le \left| {g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right)} \right| \le \varepsilon } \right\}, \end{array} $ | (16) |
式中Pr{*}表示概率。
对应的机构失效概率为
| $ \begin{array}{l} {p_{\rm{f}}} = \Pr \left\{ {\left| {g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right)} \right| > \varepsilon } \right\} = \Pr \left\{ {g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) > } \right.\\ \left. {\varepsilon \cup g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) < - \varepsilon } \right\}。\end{array} $ | (17) |
据前述,当机构随机尺寸变量标准差σX相对于尺寸均值μX较小时,采用一次二阶矩方法(First Order and Second Moment, FOSM)对式(16)和式(17)求解具有足够的精度。于是机构运动可靠度为
| $ R = \mathit{\Phi }\left( {{\beta ^ + }} \right) - \mathit{\Phi }\left( {{\beta ^ - }} \right)。$ | (18) |
对应的失效概率为
| $ {P_{\rm{f}}} = 1 - R, $ | (19) |
式中:Φ(*)为标准正态分布;β+和β-为可靠性指标且
前述点可靠度仅仅给出了在某一特定时刻机构运动输出满足期望运动输出的可能性,每个时刻点的机构可靠度是相互独立的,因而它忽略了在这一指定时刻以前机构的运动是否失效。近来,有学者提出了一种随时间关联机构运动可靠度,即机构运动时变可靠度。这种可靠度考虑的是机构在期望运动期间上其运动误差小于指定的误差限ε,即
| $ \begin{array}{l} R\left( {{\varphi _0},{\varphi _{\rm{f}}}} \right) = \mathit{Pr} \left\{ {\left| {g\left( {\mathit{X},{\varphi _1}} \right)} \right| \le \varepsilon ,{\varphi _1} \in \left[ {{\varphi _0},{\varphi _{\rm{f}}}} \right]} \right\} = \\ \Pr \left\{ { - \varepsilon \le g\left( {\mathit{X},{\varphi _1}} \right) \le \varepsilon ,{\varphi _1} \in \left[ {{\varphi _0},{\varphi _{\rm{f}}}} \right]} \right\}。\end{array} $ | (20) |
机构的时变失效概率则为
| $ \begin{array}{l} {P_{\rm{f}}}\left( {{\varphi _0},{\varphi _{\rm{f}}}} \right) = \Pr \left\{ {\left| {g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right)} \right| > \varepsilon ,{\varphi _1} \in \left[ {{\varphi _0},{\varphi _{\rm{f}}}} \right]} \right\} = \\ \Pr \left\{ {g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) > \varepsilon \cup g\left( {\mathit{\boldsymbol{X}},{\varphi _1}} \right) < - \varepsilon ,{\varphi _1} \in \left[ {{\varphi _0},{\varphi _{\rm{f}}}} \right]} \right\}。\end{array} $ | (21) |
目前,机构时变运动可靠性分析方法在文献中很少提及,但是在结构可靠性分析相关文献中提出了多种时变(区间)可靠性分析方法。其中用得较多的计算时变可靠度的基本方法是首次穿越方法[19]。引入结构可靠性分析中上穿越率和下穿越率的概念,机构在输入区间[φ0, φf]上的时变运动可靠度R(φ0, φf)可表示为[19]
| $ \begin{array}{*{20}{c}} {R\left( {{\varphi _0},{\varphi _{\rm{f}}}} \right) = R\left( {{\varphi _0}} \right)\exp \left\{ { - \int_{{\varphi _0}}^{{\varphi _{\rm{f}}}} {\left[ {{v^ + }\left( {{\varphi _1}} \right) + } \right.} } \right.}\\ {\left. {\left. {{v^ - }\left( {{\varphi _1}} \right)} \right] \cdot {\rm{d}}{\varphi _1}} \right\},} \end{array} $ | (22) |
式中:v+(φ1)和v-(φ1)分别表示上、下穿越率;R(φ0)为输入转角φ1在初始点φ0处的点可靠度。
根据文献[12],机构运动误差过程的上、下穿越率的解析表达式为
| $ {v^ + }\left( {{\varphi _1}} \right) = \left\| {c'\left( {{\varphi _1}} \right)} \right\|\varphi \left[ {{\beta _ + }\left( {{\varphi _1}} \right)} \right]\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left[ {\frac{{{{\beta '}_ + }\left( {{\varphi _1}} \right)}}{{\left\| {c'\left( {{\varphi _1}} \right)} \right\|}}} \right], $ | (23) |
式中Ψ(x)=φ(x)-xΦ(x)。
| $ {v^ - }\left( {{\varphi _1}} \right) = \left\| {c'\left( {{\varphi _1}} \right)} \right\|\varphi \left[ {{\beta _ - }\left( {{\varphi _1}} \right)} \right]\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left[ {\frac{{{{\beta '}_ - }\left( {{\varphi _1}} \right)}}{{\left\| {c'\left( {{\varphi _1}} \right)} \right\|}}} \right]。$ | (24) |
由式(23)和(24),机构误差过程上、下穿越率的求解需c′(φ1)、β+(φ1)、β-(φ1)、β′+(φ1)和β′-(φ1)。其中,c(φ1)定义为矢量b(φ1)的单位矢量,因此有
| $ \begin{array}{l} c'\left( {{\varphi _1}} \right) = {\left[ {\frac{{\mathit{\boldsymbol{b}}\left( {{\varphi _1}} \right)}}{{\left\| {\mathit{\boldsymbol{b}}\left( {{\varphi _1}} \right)} \right\|}}} \right]^\prime } = \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\sigma _g}\left( {{\varphi _1}} \right)\mathit{\boldsymbol{b'}}\left( {{\varphi _1}} \right) - \mathit{\boldsymbol{b}}\left( {{\varphi _1}} \right){{\sigma '}_g}\left( {{\varphi _1}} \right)}}{{\sigma _g^2\left( {{\varphi _1}} \right)}}。\end{array} $ | (25) |
在式(25)中,σ′g(φ1)由式(15)导出,即
| $ {{\sigma '}_g}\left( {{\varphi _1}} \right) = \frac{{\mathit{\boldsymbol{b}}\left( {{\varphi _1}} \right) \cdot \mathit{\boldsymbol{b'}}\left( {{\varphi _1}} \right)}}{{{\sigma _g}\left( {{\varphi _1}} \right)}}, $ | (26) |
其中,
| $ b'\left( {{\varphi _1}} \right) = - \frac{{{{\left( {\mathit{\boldsymbol{H'}}} \right)}^{\rm{T}}}T - {\mathit{\boldsymbol{H}}^{\rm{T}}}T'}}{{{T^2}}} \cdot {\sigma _X}, $ | (27) |
其中,(H′)T和T′分别为
| $ \begin{array}{l} {\left( {\mathit{\boldsymbol{H'}}} \right)^{\rm{T}}} = \\ \left[ \begin{array}{l} - 2{a_4}\sin {\theta _2} \cdot Q - 2{a_2}\sin {\theta _1}\\ - 2{a_1}\sin {\theta _1} + 2{a_4}\sin \left( {{\theta _1} - {\theta _2}} \right) \cdot \left( { - 1 - Q} \right)\\ 0\\ - 2{a_1}\sin {\theta _2} \cdot Q + 2{a_2}\sin \left( {{\theta _1} - {\theta _2}} \right) \cdot \left( { - 1 - Q} \right) \end{array} \right], \end{array} $ | (28) |
| $ T' = 2{a_1}{a_4}\cos {\theta _2} \cdot Q + 2{a_2}{a_4}\cos \left( {{\theta _1} - {\theta _2}} \right) \cdot \left( { - 1 - Q} \right), $ | (29) |
| $ \begin{array}{l} Q = \frac{{\partial {\theta _2}}}{{\partial {\theta _1}}} \cdot \frac{{\partial {\theta _1}}}{{\partial {\varphi _1}}} = \frac{{\partial {\theta _2}}}{{\partial {\varphi _1}}} = \\ - \frac{{{a_1}{a_2}\sin {\theta _1} + {a_2}{a_4}\sin \left( {{\theta _1} - {\theta _2}} \right)}}{{{a_1}{a_4}\sin {\theta _2} + {a_2}{a_4}\sin \left( {{\theta _1} - {\theta _2}} \right)}}。\end{array} $ | (30) |
β′+(φ1)、β′-(φ1)分别由
| $ \begin{array}{l} {{\beta '}_ + }\left( {{\varphi _1}} \right) = \\ \frac{{ - {\sigma _g}\left( {{\varphi _1}} \right){{\mu '}_g}\left( {{\varphi _1}} \right) - \left[ {\varepsilon - {\mu _g}\left( {{\varphi _1}} \right)} \right]{{\sigma '}_g}\left( {{\varphi _1}} \right)}}{{\sigma _g^2\left( {{\varphi _1}} \right)}}, \end{array} $ | (31) |
| $ \begin{array}{l} {{\beta '}_ - }\left( {{\varphi _1}} \right) = \\ \frac{{{\sigma _g}\left( {{\varphi _1}} \right){{\mu '}_g}\left( {{\varphi _1}} \right) - \left[ {\varepsilon + {\mu _g}\left( {{\varphi _1}} \right)} \right]{{\sigma '}_g}\left( {{\varphi _1}} \right)}}{{\sigma _g^2\left( {{\varphi _1}} \right)}}, \end{array} $ | (32) |
式中μ′g(φ1)由式(7)导出。
结合转角关系θ1=π/2-β-φ1和θ2=π/2+β-φ2可求得μ′g(φ1)为
| $ \begin{array}{l} {{\mu '}_g}\left( {{\varphi _1}} \right) = - Q\left| {_{{\mu _X}}} \right. - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\left[ {1 + {{\left( {\cot {\varphi _1} + \rho } \right)}^2}} \right] \cdot {{\sin }^2}\left( {{\varphi _1}} \right)}}。\end{array} $ | (33) |
综上,在求得了转向机构的b(φ1)、b′(φ1)、μg(φ1)、σg(φ1)和σ′g(φ1)之后,进一步求得c′(φ1)、β+(φ1)、β-(φ1)、β′+(φ1)和β′-(φ1),进而应用式(23)、(24)可求得转向机构误差过程上、下穿越率,结合初始点的点可靠度R(φ0)利用式(22)即可求解转向机构的时变运动可靠度(或失效概率)。
3 转向机构的优化综合 3.1 转向机构确定性综合转向机构优化综合目的在于确定机构结构尺寸以使实际输出与期望输出之间的误差尽量小。由于转向机构底杆尺寸AD(即a1)是由每款型号汽车的长、宽及最小转弯半径等因素决定,故常取a1为定值。此外,转向机构为等腰梯形机构即a2≡a4。因此,转向机构的实际设计变量仅为a2、a3、β。但为了便于描述,机构综合的设计变量仍确定为
| $ Z = {\left( {{a_1},{a_2},{a_3},{a_4},\beta } \right)^{\rm{T}}}。$ | (34) |
目标函数为机构运动输出误差,即
| $ f\left( Z \right) = \min \sum\limits_{i = 1}^n {g{{\left( {X,{\varphi _{1i}}} \right)}^2}} 。$ | (35) |
约束函数确定为机构结构约束和传力性能约束,即
| $ {g_{\rm{c}}}\left( Z \right) = \left\{ \begin{array}{l} {g_{{\rm{c1}}}}\left( X \right) = - {a_1} - {a_2} + {a_3} + {a_4} \le 0,\\ {g_{{\rm{c2}}}}\left( X \right) = - {a_1} + {a_2} - {a_3} + {a_4} \le 0,\\ {g_{{\rm{c3}}}}\left( X \right) = 0.11{a_1} - {a_2} \le 0,\\ {g_{{\rm{c4}}}}\left( X \right) = - 0.15{a_1} + {a_2} \le 0,\\ {g_{{\rm{c5}}}}\left( X \right){\cos ^{ - 1}}\left( y \right) - \frac{{{{155}^ \circ }}}{{{{180}^ \circ }}}{\rm{ \mathsf{ π} }} \le 0。\end{array} \right. $ | (36) |
式中
以及边界约束
| $ Z_{\rm{k}}^L \le {Z_{\rm{k}}} \le Z_{\rm{k}}^U,\left( {k = 1,2, \cdots ,5} \right)。$ | (37) |
考虑转向机构几何尺寸参数X=(a1, a2, a3, a4)为随机设计变量,则可根据前述确定性设计模型建立其可靠性设计模型。其设计变量为
| $ Z = {\left( {{\mu _X},\beta } \right)^{\rm{T}}} = {\left( {{\mu _1},{\mu _2},{\mu _3},{\mu _4},\beta } \right)^{\rm{T}}}, $ | (38) |
式中:μX=(μ1, μ2, μ3, μ4)为尺寸随机变量X的均值;β为方位角且为确定性设计变量。
目标函数为机构运动可靠度或者失效概率,即
| $ f\left( Z \right) = \min \left( {\max {p_{\rm{f}}}\left( {{\varphi _i}} \right)} \right), $ | (39) |
或者
| $ f\left( Z \right) = \min {p_{\rm{f}}}\left( {{\varphi _0},{\varphi _{\rm{f}}}} \right), $ | (40) |
式中:pf(φi)为机构运动点可靠度,pf(φ0, φf)为机构运动时变可靠度。
约束函数为
| $ {g_{\rm{R}}}\left( Z \right) = \left\{ \begin{array}{l} \max {p_{\rm{f}}}\left( {{\varphi _{\rm{i}}}} \right) \le p_{\rm{f}}^ * ,\\ \Pr \left\{ {{g_{{\rm{c}}i}}\left( X \right) > 0} \right\} \le p_{{\rm{f}}i}^ * \end{array} \right.\;\;\;\;\left( {i = 1,2, \cdots ,5} \right)。$ | (41) |
或者
| $ {g_{\rm{R}}}\left( Z \right) = \left\{ \begin{array}{l} {p_{\rm{f}}}\left( {{\varphi _{\rm{0}}},{\varphi _{\rm{f}}}} \right) \le p_{\rm{f}}^ * ,\\ \Pr \left\{ {{g_{{\rm{c}}i}}\left( X \right) > 0} \right\} \le p_{{\rm{f}}i}^ * , \end{array} \right.\;\;\;\;\left( {i = 1,2, \cdots ,5} \right)。$ | (42) |
式中:pf*和pfi*均为允许失效概率;Pr{gci(X)>0}为整体式转向机构的不等式约束的点失效概率。
在上述式(39)~(42)中,式(39)与式(41)组合构成机构运动点可靠性综合模型,式(40)与式(42)组合构成机构运动时变可靠性综合模型。此外,设计模型仍应包含边界约束条件,即
| $ \left\{ \begin{array}{l} \mu _j^L \le {\mu _j} \le \mu _j^U,\\ {\beta ^L} \le \beta \le {\beta ^U}。\end{array} \right. $ | (43) |
式中:μjL≤μj≤μjU为尺寸均值μj(j=1, 2, 3, 4)的边界约束;βL≤β≤βU为方位角β的边界约束。
4 数值实例根据图 2,假定转向机构梯形臂AB为主动件,定义梯形臂AB转角为机构运动输入转向角φ1p(φ1p=φ1),另一侧则为机构运动输出转向角φ2。输入转向角范围(区间)为[0°,38°],尺寸变量的标准差根据“3σ”原则确定,取σ1=0.4 mm,σ2=0.167 mm,σ3=0.4 mm,σ4=0.167 mm。允许输出转向角误差极限为ε=0.85°。取时变可靠性优化综合模型时变失效概率极限pf*=7×10-3、pfj*=7×10-3(j=1, 2, …, 5)。
据前述,机构综合时取转向梯形机构底杆尺寸a1为定值(取a1=128 5 mm),则在可靠性优化综合中其均值μ1=128 5 mm,并设定a2≡a4。取设计变量下界为ZL=(100 mm, 1 285 mm, 100 mm, 50),上界为ZU=(200 mm, 12 850 mm, 200 mm, 250)。在确定性综合和点可靠性综合中设计点数确定为m=38,时变可靠性综合优化设计不需要设计点数,因为它以整个区间为考虑对象。根据上述设定和前述三类综合模型求解得到转向机构的优化解见表 1和表 2。表 1和表 2中,点可靠性和时变可靠性优化解是以确定性优化解为初始设计点求得的。
| 表 1 确定性优化综合解 |
| 表 2 可靠性优化综合解 |
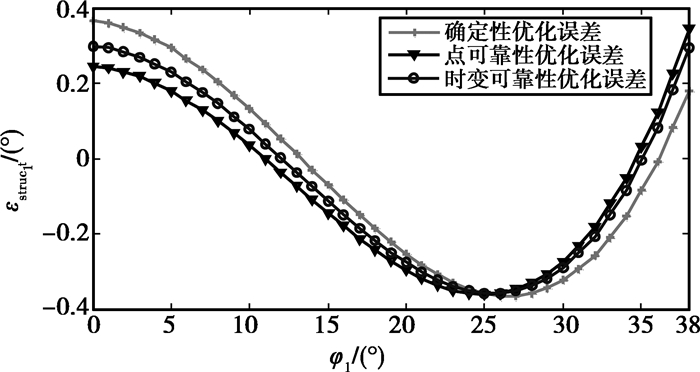
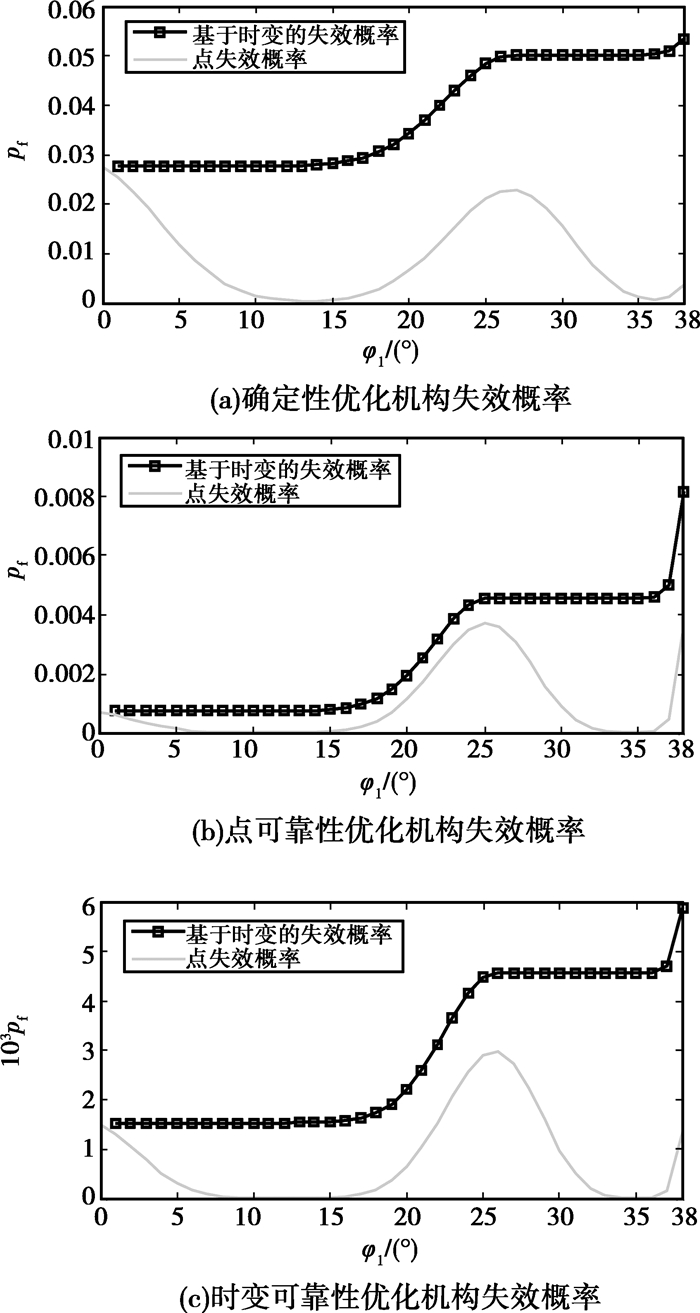
针对1中3种优化方法求得的优化解对机构进行可靠性分析。3组机构的结构误差曲线如图 3所示,其失效概率曲线如图 4所示。在图 4中,(a)、(b)、(c)分别表示为确定性综合、点可靠性综合和时变可靠性综合的点失效概率和时变失效概率。3种优化方法所得到的机构在输入区间[00, 380]上的时变失效概率、最大点失效概率及最大结构误差见表 3。
|
图 3 机构结构误差 |
| 表 3 失效概率和结构误差 |
|
图 4 机构运动失效概率 |
对以上数据和曲线的分析比较,可得到以下结论:
1) 从图 4可以看到3种优化方法所得机构的在整个输入区间[00, 380]上的时变失效概率都分别大于其点失效概率,当点失效概率呈上升趋势时,时变失效概率也上升,当点失效概率下降或者保持不变时,时变失效概率曲线变得平缓并有缓慢上升趋势。
2) 结合3组机构的误差曲线和失效概率曲线,可知点失效概率是根据时间(转向输入角区间)而变化的(有增大也有减小)。并且点失效率的变化主要由结构误差引起,当结构误差绝对值呈上升趋势时点失效概率上升,当结构误差绝对值呈下降趋势时点失效概率下降,且在误差达到极值点时点失效概率也为一极值。
3) 从表 3数据可知确定性优化设计出的机构其时变失效概率为5.338×10-2,点可靠性优化机构时变失效概率为8.156×10-3,这两者均大于设计要求pf*=7×10-3。只有时变可靠性优化方法设计出的机构失效概率小于pf*=7×10-3为5.873×10-3,满足以整个区间可靠性为对象的设计要求。并且从点可靠性优化机构失效概率可知,其点失效概率为3.711×10-3小于pf*=7×10-3,但其时变失效概率为8.156×10-3大于pf*=7×10-3,表明满足点可靠度要求并不一定满足时变可靠度要求;相反的,时变可靠性优化机构其时变失效概率为5.873×10-3,点失效概率为2.963×10-3,表明满足时变可靠度要求一定满足点可靠度要求。
4) 从比较数据可以知道,当以确定性优化解作为点可靠性优化和时变可靠性优化的初始设计变量时,机构的结构误差为:“确定性优化>点可靠性优化>时变可靠性优化”,而时变失效概率和点失效概率也同样为:“确定性优化>点可靠性优化>时变可靠性优化”。表明若以一组较为准确的参数作为时变可靠性优化方法的初始点,时变可靠性优化方法设计出的机构不仅结构误差最小,其点失效概率和时变失效概率也最小(可靠度最大)。
5 结论针对转向机构的运动精度问题,以整体式转向机构为研究对象,应用随机过程理论和机构运动时变可靠性理论对机构运动误差过程以及机构运动可靠性进行了研究,提出了考虑机构系统中不确定性的真实机构设计方法。主要研究工作及所得出的结论如下:
1) 考虑构件尺寸的不确定性(随机性),建立了包含结构误差的机构运动误差概率模型,对其统计特征分析表明机构运动输出为非平稳高斯过程。
2) 将现有机构运动时变可靠性理论拓展应用到汽车转向机构的运动可靠性分析。在机构运动误差概率模型研究的基础上,导出了求解上穿越率和下穿越率的解析模型,并由此建立了转向机构运动时变可靠度的分析模型。
3) 结合转向机构运动时变可靠度的分析模型,建立了整体式转向机构的概率综合模型。通过数值实例,对整体式转向机构的确定性优化综合、点可靠性综合和时变可靠性优化综合进行了对比研究。研究结果表明,机构的时变运动可靠性综合在保证机构运动高精度和高可靠性方面具有明显的优势。机构的时变可靠性综合在有效处理机构系统不确定性的同时能明显减小机构的结构误差、提高机构运动精度和可靠性。此外,由于机构的时变可靠性综合在给定的整个运动区间上考虑机构系统的运动精度,其求解过程不需要对区间进行离散,因此该综合方法所得到的优化解具有稳健性。
4) 从机构的点可靠性和时变可靠性分析的对比研究看,机构时变可靠度总是小于等于点可靠度,因此满足点可靠度并不意味着满足时变可靠度。由此表明,在考虑不确定性真实机构的运动分析与综合中,运用机构时变运动可靠性理论比传统的点可靠性更加合理,它能够从机构的整个运动区间上考察其运动输出满足期望输出的可能性。这为该精度和高可靠性机构设计提供了新的理论和方法。
| [1] | Wolfe W A. Analytical design of an Ackermann steering linkage[J]. Transactions ASME Journal of Engineering for Industry, 1959, 11: 11–14. |
| [2] | Yao J, Angeles J. The kinematic synthesis of steering mechanisms[J]. Transactions of the CSME, 2000, 24: 453–476. |
| [3] | Simionescu P A, Beale D. Optimum synthesis of the four-bar function generator in its symmetric embodiment:the Ackermann steering linkage[J]. Mechanism and Machine Theory, 2002, 37(12): 1487–1504. DOI:10.1016/S0094-114X(02)00071-X |
| [4] | Bian X L, Song B A, Becker W. The optimisation design of the McPherson strut and steering mechanism for automobiles[J]. Forschung im Ingenieurwesen, 2003, 68(1): 60–65. DOI:10.1007/s10010-003-0107-6 |
| [5] | Lin J G, Yang J, Zhang W M. Comparative study on optimization design methods of steering mechanism[J]. Advanced Materials Research, 2012, 490/491/492/493/494/495: 2191–2195. |
| [6] |
王朝兵, 陈小安, 陈宏, 等.
误差随机性对行星齿轮系传动精度的影响特性[J]. 重庆大学学报, 2012, 35(9): 41–47.
WANG Chaobing, CHEN Xiaoan, CHEN Hong, et al. Influence of error's randomness on transmission accuracy of planetary gear[J]. Journal of Chongqing University, 2012, 35(9): 41–47. DOI:10.11835/j.issn.1000-582X.2012.09.007 (in Chinese) |
| [7] | Hanzaki A R, Rao P V M, Saha S K. Kinematic and sensitivity analysis and optimization of planar rack-and-pinion steering linkages[J]. Mechanism and Machine Theory, 2009, 44(1): 42–56. DOI:10.1016/j.mechmachtheory.2008.02.014 |
| [8] | Huang X Z, Zhang Y M. Reliability sensitivity analysis for rack-and-pinion steering linkages[J]. ASME Journal of Mechanical Design, 2010, 132(7): 071012. DOI:10.1115/1.4001901 |
| [9] |
龙进, 张均富, 王进戈.
平面四杆转向机构运动可靠性灵敏度分析[J]. 机械设计与研究, 2011, 27(6): 21–23, 26.
LONG Jin, ZHANG Junfu, WANG Jinge. The kinematic reliability sensitivity analysis of planar four-bar steering mechanism[J]. Machine Design and Research, 2011, 27(6): 21–23, 26. (in Chinese) |
| [10] |
程贤福, 吴志强, 张鑫.
车辆转向机构运动精度的可靠性稳健优化设计[J]. 机械设计与制造, 2011(3): 8–10.
CHENG Xianfu, WU Zhiqiang, ZHANG Xin. Reliability-based robust optimization design for kinematics accuracy of steering mechanism of trucks[J]. Machinery Design & Manufacture, 2011(3): 8–10. (in Chinese) |
| [11] | Cheng X F, Zhang X. The robust reliability optimization of steering mechanisn for trucks based on non-probabilistic intervel model[J]. Key Engineering Material, 2011, 467/468/469: 296–299. |
| [12] | Zhang J F, Du X P. Time-dependent reliability analysis for function generator mechanisms[J]. Journal of Mechanical Design, 2011, 133(3): 031005. DOI:10.1115/1.4003539 |
| [13] | Zhang J F, Wang J, Du X P. Time-dependent probabilistic synthesis for function generator mechanisms[J]. Mechanisms and Machine Theory, 2011, 46(9): 1236–1250. DOI:10.1016/j.mechmachtheory.2011.04.008 |
| [14] |
王如彬.
机构运动学的随机过程分析与精度的失效模型[J]. 机器人, 1991, 13(3): 19–26.
WANG Rubin. Random process analysis in mechanism kinematics and model of precision ineffectiveness[J]. Robot, 1991, 13(3): 19–26. (in Chinese) |
| [15] |
崔利杰, 吕震宙, 王奇.
概率密度演化方法在机构运动精度可靠性中的应用研究[J]. 机械科学与技术, 2010, 29(5): 690–694, 700.
CUI Lijie, Lü Zhenzhou, WANG Qi. A study of the mechanism kinematic accuracy reliability by probability density evolution method[J]. Mechanical Science and Technology, 2010, 29(5): 690–694, 700. (in Chinese) |
| [16] |
魏永祥, 陈建军, 马洪波, 等.
随机参数弹性连杆机构在平稳随机激励下的动力可靠度分析[J]. 机械工程学报, 2012, 48(2): 36–43.
WEI Yongxiang, CHEN Jianjun, MA Hongbo, et al. Dynamic reliability analysis of elastic linkage mechanism with stochastic parameters under stationary random excitation[J]. Journal of Mechanical Engineering, 2012, 48(2): 36–43. (in Chinese) |
| [17] | Wittwer J W, Chase K W, Howell L L. The direct linearization method applied to position error in kinematic linkages[J]. Mechanism and Machine Theory, 2004, 39(7): 681–693. DOI:10.1016/j.mechmachtheory.2004.01.001 |
| [18] | Bhatti P K. Probabilistic modeling and optimal design of robotic manipulators[D]. West Lafayette:Purdue University, 1989. http://docs.lib.purdue.edu/dissertations/AAI9018787/ |
| [19] | Sudret B. Analytical derivation of the outcrossing rate in time-variant reliability problems[J]. Structures and Infrastructure Engineering, 2008, 4(5): 353–362. DOI:10.1080/15732470701270058 |
 2013, Vol. 36
2013, Vol. 36

