电力电子变换器是一个强非线性系统,在实际运行过程中普遍会出现分岔与混沌等非线性现象,其主要表现为刺耳的电磁噪声、器件间歇性振荡以及突然崩溃等不规则现象[1]。近20年来,电力电子界已高度重视该领域中分岔与混沌现象的研究。1990年,Krein和Bass指出了非线性在电力电子中的重要性[2-3],并指出这些普遍存在的复杂行为可用科学手段获得,研究此类复杂行为能给电力电子系统的设计提供重要指导。
DC/DC变换器是电力电子变换器中最基本的形式之一。20世纪90年代以来,国内外大量文献对DC/DC变换器的分岔与混沌现象做了深入研究,并取得了一定的研究成果[4-17]。其研究内容主要侧重于系统的非线性动力学建模方法、稳定性分析方法以及混沌控制方法等方面,为电路的设计以及后续更复杂电力电子变换器的非线性研究奠定了基础。
H桥变换器是现代电力电子系统中的核心元件,广泛运用于现代电力行业。然而,对H桥变换器中分岔与混沌等非线性行为的研究直到21世纪初才开始起步。2002年,Robert等首次分析了电流控制模式下H桥变换器中的边界碰撞分岔现象[18],建立了H桥的离散迭代模型,详细分析了H桥中边界碰撞分岔的物理机制。之后,Robert等又将时延反馈控制(TDFC)和扩展时延反馈控制(ETDFC)方法引入到H桥的混沌控制中,对H桥的非线性行为进行控制,以达到扩大系统运行稳定域的目的[19-20]。文献[21-23]在上述研究基础上对电流峰值控制型H桥直流斩波器中的分岔与混沌现象作了详细的分析与研究。然而,上述对H桥变换器非线性的研究中选择指令电流的参考量都是直流量,实质上H桥仍然工作在DC/DC状态,其研究内容仍属DC/DC变换器的范畴。因此,为更深入地研究H桥变换器中的非线性现象,王学梅等在2009年首次将正弦信号作为H桥变换器的参考量,比较系统地分析了比例调节下H桥逆变器中出现的分岔与混沌现象[24],并在文献[25]中引入了快变和慢变两种尺度,建立H桥正弦逆变器的快变和慢变离散模型,对其混沌行为做了更深入地研究。文献[26]则对电压控制模型下H桥变换器的快标倍周期分岔现象作了系统地研究,并利用Jacobian矩阵法对系统进行了稳定性分析。文献[27]对数字控制下逆变器中出现的振荡现象作了深入地分析,揭示了出现振荡现象由于系统发生了Hopf分岔引起的,最后给出了振荡频率的解析式。上述研究的逐步深入以及研究方法的不断成熟,使得电力电子系统的设计更具有可靠性。
笔者比较系统地介绍了H桥变换器中非线性行为的研究现状。首先对H桥变换器的2种离散模型做了较详细地总结和评价;然后具体分析了常用H桥变换器的稳定性分析和数值仿真方法;同时选择H桥直流侧电压为分岔参数,利用Lyapunov指数法对上述两种模型的差异和适用性作了具体地分析,说明其差异性产生的机理;最后介绍了时延反馈控制和扩展时延反馈控制在H桥混沌控制中的具体应用,并对如何继续深入研究H桥变换器的非线性行为作了展望。
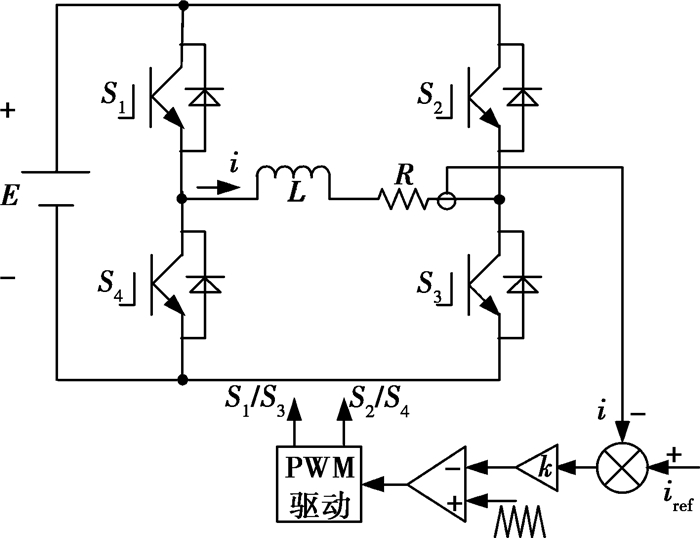
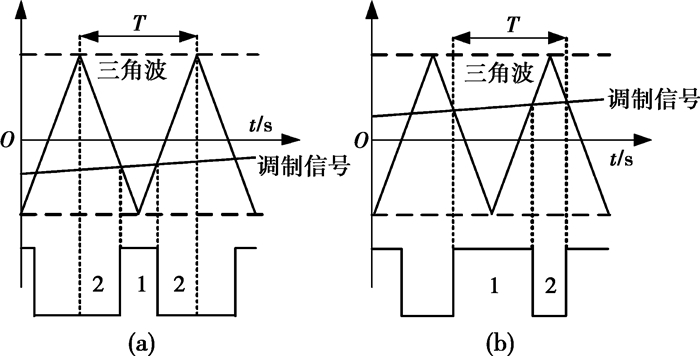
1 H桥变换器离散模型的建立典型H桥变换器的工作原理图如图 1所示,其中输入端为直流源E,经H桥变换后其输出端接阻感负载(由电阻R和电感L组成),输出电流用i表示。针对上述H桥变换器在一个开关周期T内的工作状态,设dn为第n个开关周期的占空比。Robert等根据开关的实际工作情况把一个开关周期分为3个工作阶段[18-20]。如图 2(a)所示,当nT < t≤nT+((1-dn)/2)T时,调制信号小于三角波信号,此时S2和S4导通,S1和S3关断,系统处于状态2;当nT+((1-dn)/2)T < t≤nT+((1+dn)/2)T时,调制信号大于三角波信号,此时S1和S3导通,S2和S4关断,系统处于状态1;当nT+((1+dn)/2)T < t≤(n+1)T时,系统又重新处于状态2。王学梅等则认为当开关频率远远大于调制信号频率时,可以把一个开关周期分为两个工作阶段[21-25],如图 2(b)所示,当nT < t≤(n+dn)T时,S1和S3导通,S2和S4关断,系统处于状态1;当(n+dn)T < t≤(n+1)T时,S2和S4导通,S1和S3关断,系统处于状态2。
|
图 1 H桥工作原理图 |
|
图 2 PWM原理图 |
根据上述分析,若把H桥的输出电流i作为状态变量,则系统的状态方程可以表示为
| $ \frac{{{\rm{d}}i}}{{{\rm{d}}t}} = - \frac{R}{L}i + \frac{{\left( {2\sigma - 1} \right)}}{L}E。$ | (1) |
其中σ为开关函数,由下式决定:
| $ \sigma = \left\{ \begin{array}{l} 1\;\;\;\;{s_1}\;和\;{s_3}\;导通,\\ 0\;\;\;\;{s_2}\;和\;{s_4}\;导通。\end{array} \right. $ | (2) |
利用频闪映射法可求取上述状态方程的离散迭代方程,频闪映射的基本思想是选择一个迭代初值,利用状态方程求解下一周期的解,如此不断反复,最终得到用第n个开关周期的状态变量初值表示第n+1个开关周期的状态变量初值的表达式[23],笔者利用频闪映射法求解变换器离散模型的具体过程如下(以图 2(b)为例),系统状态方程可表示为
| $ \left\{ \begin{array}{l} \dot x = {A_1}x + {B_1}E\left( {nT < t < nT + {d_n}T} \right),\\ \dot x = {A_2}x + {B_2}E\left( {nT + {d_n}T < t < \left( {n + 1} \right)T} \right)。\end{array} \right. $ | (3) |
上式在频闪映射下的离散迭代公式为
| $ \left\{ \begin{array}{l} x\left( {{t_n} + {d_n}T} \right) = = {\varphi _1}\left( {{d_n}T} \right)x\left( {{t_n}} \right) + \\ \;\;\;\;\;\int_0^{{d_n}T} {{\varphi _1}\left( {{t_n} + {d_n}T - \tau } \right){B_1}E{\rm{d}}\tau } ,\left( {t \in \left[ {{t_n},{t_n} + {d_n}T} \right]} \right);\\ x\left( {{t_{n + 1}}} \right) = = {\varphi _2}\left( {{{\bar d}_n}T} \right)x\left( {{t_n} + {d_n}T} \right) + \\ \;\;\;\;\;\int_0^{{{\bar d}_n}T} {{\varphi _2}\left( {{t_n} + T - \tau } \right){B_2}E{\rm{d}}\tau } ,\left( {t \in \left[ {{t_n} + {d_n}T,\left( {n + 1} \right)T} \right]} \right)。\end{array} \right. $ | (4) |
其中:φ1(dnT)=eA1dnT,
当A1和A2可逆时,有
| $ \left\{ \begin{array}{l} x\left( {{t_n} + {d_n}T} \right) = {\varphi _1}\left( {{d_n}T} \right)x\left( {{t_n}} \right) + \\ \;\;\;\;\;\left( {{\varphi _1}\left( {{d_n}T} \right) - 1} \right)A_1^{ - 1}{B_1}E,\\ x\left( {{t_{n + 1}}} \right) = {\varphi _2}\left( {{{\bar d}_n}T} \right)x\left( {{t_n} + {d_n}T} \right) + \\ \;\;\;\;\;\left( {{\varphi _2}\left( {{{\bar d}_n}T} \right) - 1} \right)A_2^{ - 1}{B_2}E。\end{array} \right. $ | (5) |
当A1和A2不可逆时,有
| $ \left\{ \begin{array}{l} x\left( {{t_n} + {d_n}T} \right) = {\varphi _1}\left( {{d_n}T} \right)x\left( {{t_n}} \right) + {B_1}E{d_n}T,\\ x\left( {{t_{n + 1}}} \right) = {\varphi _2}\left( {{{\bar d}_n}T} \right)x\left( {{t_n} + {d_n}T} \right) + {B_2}E\overline {{d_n}} T。\end{array} \right. $ | (6) |
根据上述频闪迭代公式即可得到系统的离散模型。
下面分别利用频闪映射法得到H桥变换器两种不同的离散模型。根据Robert等的观点[19],可得H桥变换器的主电路离散模型为
| $ {i_{n + 1}} = a{i_n} + b\left[ {2\sinh \left( {\delta {d_n}} \right) - \sinh \left( \delta \right)} \right], $ | (7) |
其中a=exp(-2δ),
同理,根据王学梅等的观点[23],可以得到在频闪映射下,H桥主电路的离散模型为
| $ {i_{n + 1}} = \left( {{i_n} - \alpha } \right)\exp \left( { - T/\tau } \right) + 2\alpha \exp \left[ { - \left( {1 - {d_n}} \right)T/\tau } \right] - \alpha , $ | (8) |
其中α=E/R,τ=L/R。
控制部分采用的是电流控制模式,为分析方便,调节器选用比例调节。控制过程如图 1所示,输出电流i的采样值与参考电流iref比较得到误差信号,误差信号经比例调节器后再与三角载波比较产生PWM信号,最后经驱动电路控制H桥各桥臂开关的通断。当参考电流iref为直流量时,H桥工作在直流斩波状态,此时系统相当于一个DC/DC斩波器;当参考电流为正弦量时,H桥工作在正弦逆变器状态,此时系统相当于一个DC/AC逆变器。于是可得占空比dn由下式决定:
| $ {d_n} = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{d_n} < 0} \right),\\ D + k\left( {{i_{{\rm{ref}}}} - {i_n}} \right)\;\;\;\;\;\left( {0 \le {d_n} \le 1} \right),\\ 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{d_n} > 1} \right); \end{array} \right. $ | (9) |
其中:D为常数;k为比例调节器的调节系数;iref为参考电流,它可以为直流量(Iref), 也可以为正弦量(iref=irefn=5sin(2πfst),其中irefn表示每个开关点的参考电流值,fs表示参数信号的频率)。因此,式(7)、(9)和式(8)、(9)组成了系统2种不同的离散迭代模型。为描述方便,以下分别称为Robert离散模型和王学梅离散模型。
通过对系统2种不同离散模型的分析可知,变换器在实际工作过程中,其三角载波的周期即为开关周期,为一个定值,则系统的开关周期应是固定的,H桥在一个固定开关周期中应出现如图 2(a)所示的3种工作状态。因此,Robert离散模型更符合系统的实际运行情况,但是在求取系统的离散模型过程中,由于在一个开关周期内需进行3次频闪映射运算,因此其运算过程较复杂,这种复杂性在更高维系统的离散建模中尤为明显。在王学梅离散模型中,考虑到开关周期远远小于调制信号周期时,调制信号在一个开关周期内可看作定值,因此两个工作状态所占用时间可认为是一个开关周期且相邻两开关周期保持不变,则在一个开关周期内系统只出现两种工作状态,如图 2(b)所示。由于在离散模型的求取过程中只需要进行两次频闪映射运算,因此简化了运算过程,但王学梅离散模型只适用于载波比较大情况下,当载波比较小时其精度会有所下降。
2 H桥变换器稳定性分析与数值仿真为分析H桥变换器的非线性行为,目前国内外文献中采用的一般步骤主要是首先建立系统离散模型,然后利用所得离散模型对系统进行稳定性分析得到其运行稳定域,再进一步通过数值分析的方法对得到的稳定域进行验证[18, 19, 23, 24]。因此,为给H桥变换器非线性研究的后续工作提供方便,有必要对现有的稳定性分析和数值仿真方法做总结和归纳。
2.1 稳定性分析在运行过程中,H桥变换器存在运行稳定域,因此对其进行稳定性分析具有实际意义。已有研究中,对H桥的稳定性分析常用的方法主要有:分岔图法[6-10, 18-24]、Lyapunov指数法[21, 22, 28]、Jacobian矩阵法[19, 20, 25]等。应用中可以根据具体条件和要求选择合适的方法对系统进行稳定性分析。
2.1.1 分岔图法利用分岔图分析H桥变换器分岔与混沌现象的具体方法为:利用系统的离散迭代模型,选择任意的迭代初值,在迭代稳定后的数个固定开关时刻对状态变量进行采样并保留采样点,将不同分岔参数值下的采样值绘制成一张图,即为系统的分岔图。
分岔图是分析变换器非线性行为常用的有效工具,它能形象地反映出随着分岔参数的变化,系统由稳定到分岔再到混沌状态的整个演化过程,并对系统运行的稳定、分岔、混沌域作了具体的划分。
2.1.2 Lyapunov指数法混沌运动的基本特点就是运动对初始条件极为敏感。两个极为接近的初值在迭代过程中所产生的轨道,随时间推移按指数方式分离,Lyapunov指数正是描述这种现象的定量指标[30],其具体定义为:描述相邻点之间的距离在多次迭代中平均每次迭代所引起的指数分离中的指数。
对于一个一维的映射:xn+1=f(xn),其Lyapunov指数(LE)可以表示为
| $ LE = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\ln \left| {f'\left( {{x_i}} \right)} \right|} 。$ | (10) |
当LE < 0时,相邻点最终靠近合并成一点,此时对应以系统的稳定状态;当LE>0时,相邻点最终按指数分离,意味着系统处于不稳定状态。LE由负变正表示系统由稳定到不稳定转变,因此,LE=0对应于系统稳定与不稳定的分界点,即分岔点。
2.1.3 Jacobian矩阵法通过系统不动点的Jacobian矩阵的最大模特征值能比较准确地判断系统的稳定性。其具体步骤如下:首先建立不动点的Jacobian矩阵,对迭代模型xn+1=f(xn, dn),在平衡点处进行小信号扰动有xn=X+
| $ {{\hat x}_{n + 1}} = \frac{{\partial f}}{{\partial {x_n}}}{{\hat x}_n} + \frac{{\partial f}}{{\partial {d_n}}}{{\hat d}_n}。$ | (11) |
再由系统的开关动作函数s(xn, dn)=0可得
| $ \frac{{\partial s}}{{\partial {x_n}}}{{\hat x}_n} + \frac{{\partial s}}{{\partial {d_n}}}{{\hat d}_n} = 0, $ | (12) |
结合式(10)和(11)可得到系统的小信号模型为
| $ {{\hat x}_{n + 1}} = \left( {\frac{{\partial f}}{{\partial {x_n}}} + \frac{{\partial f}}{{\partial {d_n}}}{{\left( { - \frac{{\partial s}}{{\partial {d_n}}}} \right)}^{ - 1}}\frac{{\partial s}}{{\partial {x_n}}}} \right){{\hat x}_n}, $ | (13) |
可知系统的Jacobian矩阵为
| $ J\left( X \right) = {\left[ {\frac{{\partial f}}{{\partial {x_n}}} - \frac{{\partial f}}{{\partial {d_n}}}{{\left( {\frac{{\partial s}}{{\partial {d_n}}}} \right)}^{ - 1}}\frac{{\partial s}}{{\partial {x_n}}}} \right]_{\left( {X,D} \right)}}, $ | (14) |
由上式可以看出,要求得系统的Jacobian矩阵,首先需求出系统的单周期稳态解(X, D),其稳态解可以利用Matlab通过数值迭代的方法求得。
可见,系统的Jacobian矩阵反映的是系统前后两次小信号扰动量的关系,因此,当Jacobian矩阵的最大模特征值|λmax| < 1时,系统处于稳定状态;当|λmax|>1时,系统将处于不稳定状态。由此可知|λmax=1|为系统稳定与不稳定的分界点。通过分析分岔参数引起系统Jacobian矩阵最大模特征值的变化,可有效地对系统进行稳定性分析。
通过对上述3种方法原理的阐述,可以看出将3种方法应用于H桥变换器的混沌研究具有各自的优缺点,现归纳如表 1所示。
| 表 1 稳定性分析方法 |
在实际应用中,应当考虑各方面的综合因素(如系统的维数、复杂程度以及对系统稳定性的具体要求等),选择合适的分析方法以方便快速有效地得到系统的运行稳定域。
2.2 数值仿真方法通过稳定性分析可以得到系统运行的稳定参数域,为进一步验证所得稳定域的正确性,需通过数值仿真的方法加以验证。现有H桥变换器的研究中通常采用的数值仿真方法有时序图[19-20, 24-25]、频闪采样图[24]、折叠图[24-25]、功率谱图[25]以及相轨迹图[27]等方法。上述方法都能较好地反映出不同分岔参数值下系统的运行状态,具体归纳如表 2所示。
| 表 2 数值仿真方法 |
在介绍了稳定性分析方法的基础上,本节针对第1节中介绍的现有H桥的2种离散模型的差异性进行数值仿真对比分析。由于只选择了H桥的输出电流为状态变量,系统可看作一维系统,其迭代运算较为简单。因此可选择Lyapunov指数法对上述两种模型在不同开关频率下的稳定性进行了对比分析。
系统参数设置如下:L=12 mH,R=10 Ω,k=0.3,D=0.4,fs=50 Hz,iref=5 sin(2πfst)。选择输入电压E为分岔参数,研究输入电压E的变化与系统稳定性的关系。根据Lyapunov指数定义可得2种离散模型对应的Lyapunov指数为
| $ L{E_{\rm{R}}} = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\ln \left| {a - 2kb\delta \cosh \left( {\delta {d_n}} \right)} \right|} 。$ | (15) |
| $ \begin{array}{l} L{E_{\rm{W}}} = \mathop {\lim }\limits_{n \to \infty } \frac{1}{n}\sum\limits_{i = 0}^{n - 1} {\ln \left| {\exp \left( { - \frac{T}{\tau }} \right) - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{2\alpha KT}}{\tau }\exp \left[ {\frac{{ - \left( {1 - {d_n}} \right)T}}{\tau }} \right]} \right|。\end{array} $ | (16) |
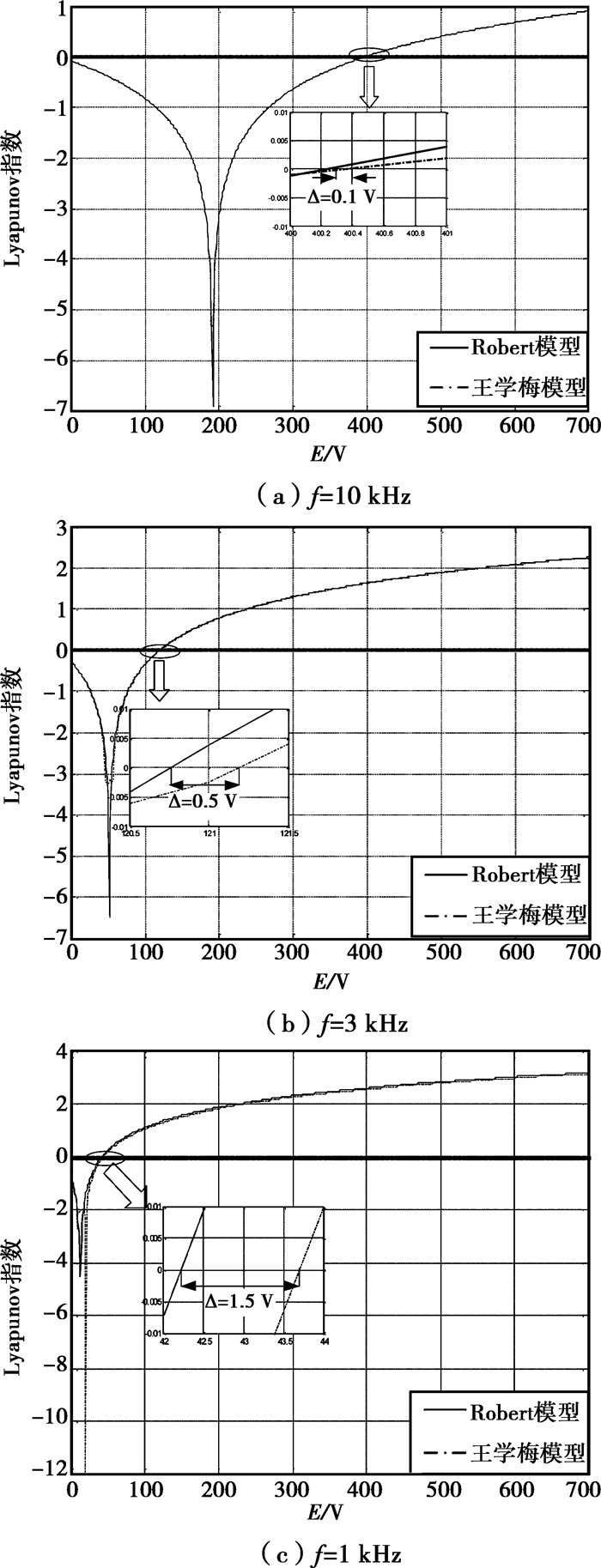
其中,LER和LEW分别为通过Robert离散模型和王学梅离散模型得到的Lyapunov指数表达式。当开关频率f分别为10,3,1 kHz时,系统的Lyapunov指数曲线如图 3所示。
|
图 3 2种模型的Lyapunov指数曲线对比图 |
图 3中小图为局部放大图(取系统稳定与不稳定分界点附近的曲线进行对比分析,横坐标为0.5 V/格),当开关频率较大时(10 kHz),所得系统的Lyapunov指数曲线基本重合,其分界点只相差Δ=0.1 V,随着开关频率的减小,王学梅离散模型所得到的Lyapunov指数曲线逐渐远离Robert离散模型的结果,精度逐渐减小,从图 3(b)和(c)中可以看出当开关频率为3kHz和1kHz时,系统稳定与不稳定的分界点分别相差0.5 V和1.5 V。这主要是由于参考信号的频率始终保持不变,而开关频率逐渐减小,载波比也随之减小,当载波比较小时,在一个开关周期内调制信号的变化已经不能忽略,因此导致王学梅所提出的离散模型的精度有所下降。
综上所述,当载波比较大时,由于可以忽略一个开关周期内调制信号的变化,因此选择王学梅所提离散模型可保证精度,并且能简化频闪映射运算;而当载波比较小时,Robert离散模型更符合系统实际运行情况,因此更具适用性。
3 H桥变换器分岔与混沌现象的控制分岔与混沌现象属于系统不稳定的一种表现,系统长期工作在不稳定状态会严重影响系统中元器件的寿命,甚至导致系统崩溃[29-31],在系统实际工作中应当尽量避免这种现象的发生。因此对H桥变换器中出现的分岔与混沌行为进行控制是一个值得深入研究的课题。
现有研究大多集中在DC/DC变换器的混沌控制中,文献[10-11]将参数共振微扰法分别应用于电压模式Buck变换器和电流模式Buck-Boost变换器的混沌控制中,以达到较好的控制效果,但由于要增加外部扰动信号电路,因此不易实现控制电路。文献[12-13]则利用OGY法分别对混沌态电压模式下的Buck变换器和电流模式下的Buck-Boost变换器进行控制,并推导出了OGY控制矢量的取值范围。文献[14-15]将Washout滤波器混沌控制技术引入到DC/DC变换器中,分别将两种实现不同功能的DC/DC变换器控制在周期稳定状态。文献[16-17]则利用时间延迟反馈控制方法对电压模式Buck变换器和峰值电流控制模式下的Boost变换器中出现的混沌现象进行控制,分析了该方法的控制机理,最终验证了该方法的有效性。
目前,国内外对H桥变换器的混沌控制方法只有文献[19, 20, 23]中提出的时延反馈和扩展时延反馈的混沌控制方法,其主要控制思想为:利用状态变量与自身延迟一定时间的参量之差去作用混沌系统,以改善系统运行状态,达到扩大系统运行稳定域的目的。由于时延反馈控制方法的硬件实现较为困难,因此目前在H桥混沌控制中的应用仍然局限于简单的仿真研究,相关文献甚少。
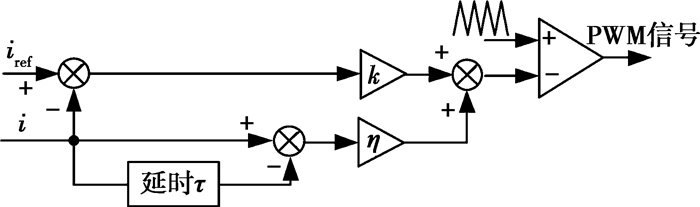
文献[19, 23]中提到的基于TDFC法的混沌控制方法,控制框图如图 4所示,具体实现方式如下:首先,给H桥变换器的原始控制信号k[Iref-i(t)]附加一时延控制信号η[i(t)-i(t-τ)],其中τ表示目标周期轨道的整数倍周期,η为可调参数。当i(t)=i(t-τ)时,附加信号消失,同时系统运动进入目标周期轨道。选择τ=T作为时延反馈控制信号的延迟时间。于是带有TDFC调节后的H桥变换器的控制占空比可以表示为
| $ {d_n} = D + k\left( {{I_{{\rm{ref}}}} - {i_n}} \right) + \eta \left( {{i_n} - {i_{n - 1}}} \right)。$ | (17) |
|
图 4 带TDFC法的控制框图 |
结合主电路模型(式(7))可以得出,此时整个系统的离散模型为
| $ \left\{ \begin{array}{l} {i_{n + 1}} = a{i_n} + b\left[ {2\sinh \left( {\delta {d_n}} \right) - \sinh \left( \delta \right)} \right],\\ {d_n} = D + k\left( {{I_{{\rm{ref}}}} - {i_n}} \right) + \eta \left( {{i_n} - {i_{n - 1}}} \right)。\end{array} \right. $ | (18) |
进一步可以求出系统在不动点(XQ, DQ)处的Jacobian矩阵为
| $ \begin{array}{l} \mathit{\boldsymbol{J}}\left( {{X_{\rm{Q}}},{D_{\rm{Q}}}} \right) = \\ \left[ {\begin{array}{*{20}{c}} {a + 2b\left( {\eta - k} \right)\cosh \left( {\delta {D_{\rm{Q}}}} \right)}&{ - 2b\eta \delta \cosh \left( {\delta {D_{\rm{Q}}}} \right)}\\ 1&0 \end{array}} \right]。\end{array} $ | (19) |
由于上述Jacobian矩阵的最大模特征值中含有η,因此,可以通过选择合适的η值来调整系统Jacobian矩阵的最大模特征值,使其过“1”点作出适当移动,以达到扩大系统运行稳定域的目的。最终使原本处于不稳定状态的系统向稳定状态转变。
文献[20]则是利用ETDFC法对系统进行混沌控制,其实现方式与TDFC法基本相似。只是将第n个开关周期的占空比调整如下:
| $ {d_n} = D + k\left( {{I_{{\rm{ref}}}} - {i_n}} \right) + \eta \left[ {{i_n} - \left( {1 - r} \right)\sum\limits_{m = 1}^n {{r^{m - 1}}{i_{n - m}}} } \right]。$ | (20) |
其中η和0 < r < 1是保证系统稳定的控制参数。同样可以求取系统Jacobian矩阵为
| $ \mathit{\boldsymbol{J'}}\left( {{X_{\rm{Q}}},{D_{\rm{Q}}}} \right) = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ {{J_1}}&{{J_2}}&{{J_3}}\\ { - \eta }&\eta &r \end{array}} \right]。$ | (21) |
其中:J1=-2bηδcosh(δDQ),J2=a+2b(η-k)δcosh(δDQ),J3=2brδcosh(δDQ)。可以发现在系统Jacobian矩阵最大模特征值中也含有参数η和0 < r < 1。因此,可以选择合适的控制参数值使得最大模特征值的过“1”点发生移动,即可以适当调整η和0 < r < 1的值来对系统进行有效地混沌控制。
综上所述,利用上述2种方法对系统进行混沌控制只需要知道目标轨道的周期,而无需确定目标轨道的其他信息,并且控制器设计简单易于实现,对控制对象模型要求不高,具有很好的适用性。然而,它们也存在一定的局限性。首先,加入混沌控制方法后系统的维数有所增加,TDFC法使系统变成了二维系统,而ETDFC法则使系统变成了三维系统,导致对系统进行稳定性分析复杂程度加大;其次,当系统其他参数受扰动时,该方法的抗干扰能力还有待验证;另外控制参数η以及r的取值范围也不易确定,因此怎样有效地确定出控制参数的范围也是一个值得深入研究的问题。
4 结论与展望近20年来,对电力电子系统中出现的复杂行为已经有了广泛的研究,并取得了一定的成果。DC/AC变换器广泛运用于各种电力电子系统,尤其随着现阶段分布式发电的广泛推广,DC/AC变换器更是成为系统中不可替代的核心部分。因此,不断深入研究DC/AC变换器中的复杂行为是一个具有实际意义的探索课题。
为将现有的研究结果推广并应用于实际电路的设计和分析中,以期为实际系统的设计提供参考,以下方面仍然需要做进一步深入的研究:
1) 将DC/DC变换器的非线性研究成果有效地引入到H桥变换器的研究。结合DC/DC变换器与H桥的相似性和差异性,如何将现有研究成果更全面有效地引入到H桥变换器的研究中是一个值得探索的课题。
2) 研究更复杂调节下H桥变换器的分岔与混沌现象。在实际应用中,系统通常采用PI、PD、PID等性能更好的调节器,因此研究这些调节器下H桥的分岔与混沌现象更具实用性。
3) 研究并网逆变器中出现的分岔与混沌现象。并网逆变器在分布式发电等系统中得到了广泛的应用。因此,对并网系统中的分岔与混沌现象做深入研究也是值得关注的课题。
4) 提出确定TDFC法和ETDFC法控制参数范围的有效方法。现有H桥TDFC法和ETDFC法控制参数的范围不易确定,因此如何有效确定这一控制参数的范围是一个值得深入研究的问题。
5) 由于现有的时延反馈控制方法硬件电路实现困难,因此如何有效地实现时延反馈控制的硬件系统,使其实用性更强,这是后续研究中需要深入的一个方面。同时,寻找更有效的混沌控制方法,在克服现有H桥混沌控制方法弊端的基础上能有效地对系统进行混沌控制。这也是在后续研究中需要解决的难题。
总之,在现代电力电子技术小型化、轻量化等发展主流的基础上,电力电子系统中出现的复杂行为是不可忽略的。H桥作为电力电子系统的核心元件,研究其中出现的分岔与混沌现象以及相应的混沌控制方法有着重要的实际意义和广阔的应用前景。
| [1] | Hamill D C, Jeffries D J. Subharmonics and chaos in a controlled switched-mode power converter[J]. IEEE Transactions on Circuits and Systems, 1988, 35(8): 1059–1061. DOI:10.1109/31.1858 |
| [2] | Krein P T, Bass R M. Type of instability encountered in simple power electronic circuit:unboundedness, chattering, and chaos[C]//Proceedings of the 1990 Fifth Annual Conference on Applied Power Electronics Conference and Exposition, March 11-16, 1990, Los Angeles, USA. Piscataway:IEEE Press, 1990:191-194. |
| [3] | Bass R M, Krein P T. State-plane animation of power electronic systems:a tool for understanding feedback control and stability[C]//Proceedings of the 1990 Fifth Annual Conference on Applied Power Electronics Conference and Exposition, March 11-16, 1990, Los Angeles, USA. Piscataway:IEEE Press, 1990:641-648. |
| [4] | Bernardo M D, Garefalo F, Glielmo L, et al. Switchings, bifurcations, and chaos in DC/DC converters[J]. IEEE Transactions on Circuits and Systems Ⅰ:Fundamantal Theory and Applications, 1998, 45(2): 133–141. DOI:10.1109/81.661675 |
| [5] | Bernardo M D, Vasca F. Discrete-time maps for the analysis of bifurcations and chaos in DC/DC converters[J]. IEEE Transactions on Circuits and Systems Ⅰ:Fundamantal Theory and Applications, 2000, 47(2): 130–143. DOI:10.1109/81.828567 |
| [6] | Tse C K, Bernardo M D. Complex behavior in switching power converters[J]. Proceedings of the IEEE, 2002, 90(5): 768–781. DOI:10.1109/JPROC.2002.1015006 |
| [7] |
张波, 曲颖.
电压反馈型Boost变换器DCM的精确离散映射及其分岔和混沌现象[J]. 电工技术学报, 2002, 17(3): 43–47.
ZHANG Bo, QU Ying. The precise discrete mapping of voltage-fed DCM boost converter and its bifurcation and chaos[J]. Transactions of China Electrotechnical Society, 2002, 17(3): 43–47. (in Chinese) |
| [8] |
罗晓曙, 汪秉宏, 陈关荣, 等.
DC-DC buck变换器的分岔行为及混沌控制研究[J]. 物理学报, 2003, 52(1): 12–17.
LUO Xiaoshu, WANG Binghong, CHEN Guanrong, et al. Research on bifurcation behavior and chaos control in DC-DC buck converter[J]. Acta Physica Sinica, 2003, 52(1): 12–17. DOI:10.7498/aps.52.12 (in Chinese) |
| [9] |
戴栋, 马西奎, 李小峰.
一类具有两个边界的分段光滑系统中边界碰撞分岔现象及混沌[J]. 物理学报, 2003, 52(11): 2729–2736.
DAI Dong, MA Xikui, LI Xiaofeng. Border collision bifurcations and chaos in a class of piecewise smooth systems with two boundaries[J]. Acta Physica Sinica, 2003, 52(11): 2729–2736. DOI:10.3321/j.issn:1000-3290.2003.11.015 (in Chinese) |
| [10] |
罗晓曙, 汪秉宏, 陈关荣, 等.
DC-DC buck变换器的分岔行为及混沌控制研究[J]. 物理学报, 2003, 52(1): 12–17.
LUO X S, WANG B H, CHEN G R, et al. Research on bifurcation behavior and chaos control in DC-DC buck converter[J]. Acta Physica Sinica, 2003, 52(1): 12–17. DOI:10.7498/aps.52.12 (in Chinese) |
| [11] | Zhou Y F, Iu H H C, Tse C K, et al. Controlling chaos in DC/DC converters using optimal resonant parametric perturbation[J]. IEEE International Symposium on Circuits and Systems, 2005, 3: 2481–2484. |
| [12] | Ivan C, Serbanescu A. Control methods on unstable periodic orbits of a chaotic dynamical system-control chaos in buck converter[C]//Proceedings of the 200811th International Conference on Optimization of Electrical and Electronic Equipment, May 22-24, 2008, Brasov, Romania. Piscataway:IEEE Press, 2008:63-68. |
| [13] |
王利清, 魏学业, 温伟刚, 等.
混沌态电流模式Buck-Boost开关变换器的OGY控制[J]. 信息与控制, 2005, 34(6): 742–745.
WANG Liqing, WEI Xueye, WEN Weigang, et al. OGY control of the chaotic current mode buck-boost switching converter[J]. Information and Control, 2005, 34(6): 742–745. (in Chinese) |
| [14] |
汪剑鸣, 许镇琳.
PWM型DC/DC变换器的Washout滤波器混沌控制方法[J]. 信息与控制, 2005, 34(3): 269–273.
WANG Jianming, XU Zhenlin. Controlling chaos in PWM DC/DC converter with washout filter[J]. Information and Control, 2005, 34(3): 269–273. (in Chinese) |
| [15] | Ma W, Wang M Y, Liu S X, et al. Stabilizing the average-current-mode-controlled boost PFC converter via washout-filter-aided method[J]. IEEE Transactions on Circuits and SystemsⅡ:Express Briefs, 2011, 58(9): 595–599. DOI:10.1109/TCSII.2011.2161170 |
| [16] |
杨汝, 张波.
DC-DC buck变换器时间延迟反馈混沌化控制[J]. 物理学报, 2007, 56(7): 3789–3795.
YANG Ru, ZHANG Bo. Chaotification control of buck converter via time-delayed feedback[J]. Acta Physica Sinica, 2007, 56(7): 3789–3795. DOI:10.7498/aps.56.3789 (in Chinese) |
| [17] |
卢伟国, 周雒维, 罗全明.
电压模式BUCK变换器输出延迟反馈混沌控制[J]. 物理学报, 2007, 56(10): 5648–5654.
LU Weiguo, ZHOU Luowei, LUO Quanming. Output time-delay feedback control of chaos in voltage-mode BUCK converter[J]. Acta Physica Sinica, 2007, 56(10): 5648–5654. DOI:10.3321/j.issn:1000-3290.2007.10.016 (in Chinese) |
| [18] | Robert B, Robert C. Border collision bifurcations in a one-dimensional piecewise smooth map for a PWM current-programmed H-bridge inverter[J]. International Journal of Control, 2002, 75(16/17): 1356–1367. |
| [19] | Iu H H C, Robert B. Control of chaos in a PWM current-mode H-bridge inverter using time-delayed feedback[J]. IEEE Transations on Circuits and Systems Ⅰ:Fundamantal Theory and Applications, 2003, 50(8): 1125–1129. DOI:10.1109/TCSI.2003.815220 |
| [20] | Feki M, Robert B, Iu H H C. A proportional plus extended time-delayed feedback controller for a PWM inverter[C]//Proceedings of the 2004 IEEE 35th Annual Conference on Power Electronics Specialists, June 20-25, 2004, Aachen, Germany. Piscataway:IEEE Press, 2004, 5:3317-3320. |
| [21] |
王学梅, 张波.
H桥直流斩波变换器边界碰撞分岔和混沌研究[J]. 中国电机工程学报, 2009, 29(9): 22–27.
WANG Xuemei, ZHANG Bo. Mechanism of border-collision bifurcations and chaos in H-bridge direct current chopper[J]. Proceedings of the CSEE, 2009, 29(9): 22–27. (in Chinese) |
| [22] | Wang X M, Zhang B, Qiu D Y. Bifurcations and chaos in H-bridge DC chopper under peak-current control[C]//Proceedings of the 2008 IEEE International Conference on Electrical Machines and Systems, October 17-20, 2008, Wuhan, China. Piscataway:IEEE Press, 2008:2173-2177. |
| [23] | Jiang W, Zhou Y F, Chen J N, et al. Research of modeling and simulation to control chaos in H bridge converter[C]//Proceedings of the Ninth International Conference on Electronic Measurement & Instruments, August 16-19, 2009, Beijing, China. Piscataway; IEEE Press, 2009:327-331. |
| [24] |
王学梅, 张波.
单相SPWM逆变器的分岔及混沌现象分析[J]. 电工技术学报, 2009, 24(1): 101–107.
WANG Xuemei, ZHANG Bo. Study of bifurcation and chaos in single-phase SPWM inverter[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 101–107. (in Chinese) |
| [25] |
王学梅, 张波, 丘东元.
H桥正弦逆变器的快变和慢变稳定性及混沌行为研究[J]. 物理学报, 2009, 58(4): 2248–2254.
WANG Xuemei, ZHANG Bo, QIU Dongyuan. The fast-and slow-scale stabilities and chaotic motion of H-bridge sine inverter[J]. Acta Physica Sinica, 2009, 58(4): 2248–2254. DOI:10.7498/aps.58.2248 (in Chinese) |
| [26] | Li M, Dai D, Ma X K, et al. Fast scale period-doubling bifurcation in voltage-mode controlled full-bridge inverter[C]//Proceedings of the IEEE International Symposium on Circuits and Systems, May 18-21, 2008, Seattle, WA. Piscataway:IEEE Press, 2008:2829-2832. |
| [27] |
雷博, 肖国春, 吴旋律, 等.
单相全桥DC-AC电压逆变电路数字控制中的振荡现象分析[J]. 物理学报, 2011, 60(9): 122–132.
LEI Bo, XIAO Guochun, WU Xuanlü, et al. Analysis of oscillation phenomenon in digital controlled DC-AC H-bridge inverter[J]. Acta Physica Sinica, 2011, 60(9): 122–132. (in Chinese) |
| [28] |
孙媛, 李敏远.
H桥逆变器的离散建模及混沌现象的仿真研究[J]. 西安理工大学学报, 2011, 27(1): 92–96.
SUN Yuan, LI Minyuan. Simulation research on the discrete model and chaos in H-bridge inverter[J]. Journal of Xi'an University of Technology, 2011, 27(1): 92–96. (in Chinese) |
| [29] |
王新生, 王琪, 徐殿国.
DC-DC变换器中的分岔现象综述[J]. 哈尔滨工业大学学报, 2008, 40(5): 754–758.
WANG Xinsheng, WANG Qi, XU Dianguo. Bifurcation phenomena in DC-DC converters[J]. Journal of Harbin Institute of Technology, 2008, 40(5): 754–758. (in Chinese) |
| [30] | 张化光, 王智良, 黄伟. 混沌系统的控制理论[M]. 沈阳: 东北大学出版社, 2003. |
| [31] |
马西奎, 李明, 戴栋, 等.
电力电子电路与系统中的复杂行为研究综述[J]. 电工技术学报, 2006, 21(12): 1–11.
MA Xihui, LI Ming, DAI Dong, et al. Reviews of research on complex behavior of power electronic circuits and systems[J]. Transactions of China Electrotechnical Society, 2006, 21(12): 1–11. DOI:10.3321/j.issn:1000-6753.2006.12.001 (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


