1b. 北京科技大学 冶金与生态工程学院, 北京 100083;
2. 方大特钢科技股份有限公司, 南昌 330012
1b. School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Fangda Special Steel Technology Co., Ltd., Nanchang 330012, China
钢铁工业属于流程制造业,连铸工序是钢铁生产流程中的一道重要工序,其直接决定铸坯的质量。二次冷却控制是连铸工序中的一个重要环节,其控制得好坏不仅影响着连铸机的生产率,还影响着铸坯凝固组织的优劣以及铸坯的各种缺陷的形成与发展。生产高质量的铸坯不仅需要先进的二次冷却控制工艺,还需要先进的控制理念, 先进的控制理念不仅强调对生产工艺的精细控制,还强调对生产装备的精细配置以及整个生产流程的精细管控[1]。随着用户对铸坯质量要求的不断提高以及市场竞争得日益加剧,改善二次冷却制度,优化二冷配水模型,实现铸坯凝固过程的均匀冷却和精细控制显得尤为重要[1-2]。目前,现行的连铸二冷配水模型在控制二冷各段水量时,主要考虑铸坯拉速和钢水过热度的变化对水量的影响,而很少考虑钢水成分波动对凝固过程的影响。通过钢厂的MES系统,能准确掌握每一炉钢水的成分信息和过热度信息,笔者在此基础上对传统的二冷参数配水控制模型进行了改进,提出了新的二冷控制模型,并对改进前后的两种配水控制模型在钢水成分发生变化情况下的模拟计算结果进行了对比分析。
1 现行二冷控制模型现行的连铸二冷控制模型主要分为静态控制模型和动态控制模型两大类。目前,国内的连铸机二冷区水量主要采用的是静态控制模型,主要包括:比例配水模型,其控制模型见式(1),二冷各段水量与拉速为直线关系;参数配水模型,其控制模型见式(2)的二次曲线模型,参数配水模型相对于比例配水模型更能满足连铸生产的要求,进而提高铸坯的质量。随着测温技术的进步,连铸浇铸过程中间包钢水温度的变化也参与到二冷区水量控制模型之中,其控制模型见式(3)和式(4)[3-5],控制模型(4)中不仅考虑到了实时的过热度,还考虑了不同季节二冷水温的变化对铸坯凝固传热的影响,这两种控制模型都是在参数配水模型上进行了改进和优化,考虑了更多的生产因素,也使模型的可靠性得到进一步提高,于是发展了参数配水模型。上述相应的控制模型如下:
| $ {Q_i} = {K_i}V, $ | (1) |
| $ {Q_i} = {A_i}{V^2} + {B_i}V + {C_i}, $ | (2) |
| $ {Q_i} = {A_i}{V^2} + {B_i}V + {C_i} + {D_i}\Delta T, $ | (3) |
| $ {Q_i} = K\left( {{A_i}{V^2} + {B_i}V + {C_i}} \right) + {D_i}\Delta T + {F_i}。$ | (4) |
式中:Qi为第i个冷却段的水量,L/min;Ki为第i个冷却段的参数;V为实时拉速,m/min;ΔT为钢水的实时过热度,℃;Ai,Bi,Ci,Di为与钢种及工况条件有关的参数,可通过建立水量计算模型及回归分析得到;Fi为与二冷水温有关的参数,与季节因素有关。
上文介绍的各参数配水模型,确定了各冷却段的配水参数之后,在拉速及过热度保持平稳或变化幅度较小的情况下生产可以满足铸坯质量的要求,然而当拉速或浇铸温度有较大的波动时,铸坯表面温度就会出现较大的波动,进而引起铸坯出现质量问题。针对拉速变化较大的不稳定生产,在参数控制模型的基础上,前人引入以坯龄模型为基础的有效拉速的概念,把模型中的平均拉速用有效拉速来代替,实现动态水量控制。这样在拉速发生较大变动时的非稳态浇铸下,有效拉速法使表面温度波动更加平稳[6],其控制模型见式(5);针对浇注过程钢水温度发生较大波动的不稳定生产,窦志超等[6-7]在控制模型(5)的基础上,借鉴有效拉速的思想对过热度进行改进提出了有效过热度的概念,建立了基于有效拉速与有效过热的综合二冷配水控制模型,其控制模型见式(6),其研究结果表明,铸坯表面温度比用实时过热度补偿时更趋平稳。上述两种控制模型既可以满足稳定生产对铸坯质量的要求,也可以满足生产工艺参数经常变化的不稳定生产,其相应控制方程如下:
| $ {Q_i} = {A_i}V_{{\rm{e}}i}^2 + {B_i}{V_{{\rm{e}}i}} + {C_i} + {D_i}\Delta T, $ | (5) |
| $ {Q_i} = {A_i}V_{{\rm{e}}i}^2 + {B_i}{V_{{\rm{e}}i}} + {C_i} + {D_i}\Delta {T_{{\rm{e}}i}}, $ | (6) |
式中:Qi为第i个冷却段的水量,L/min;Vei为第i冷却段的有效拉速,m/min;ΔT为钢水实时过热度,℃;ΔTei为第i个冷却段的有效过热度,℃;Ai,Bi,Ci,Di分别为与钢种及工况条件有关的参数,可通过建立水量计算模型及回归分析得到。
除了上述介绍的基于“有效控速”及“有效过热度”的动态水量控制模型,一般的动态水量控制模型是依据目标表面温度反馈实施水量分配,根据铸坯表面温度反馈的方式又可分为:在线测温器实测温度反馈和在线模型实时计算温度反馈两种模型[8-10]。在线测温器实测温度反馈的动态配水模型,由于二冷区往往存在大量的水蒸气,使得目前的测温设备不能准确直接测得铸坯表面的实时温度,因而这种模型的应用受到了很大的限制。目前,实际应用的多是在线模型实时计算铸坯表面温度进行反馈的动态配水模型,这种模型的应用需要复杂的计算机系统,对设备要求较高。
2 新型二冷控制模型的建立与求解钢水窄成分精细控制作为生产目标之一,而在实际生产中有许多不确定的因素会导致钢水成分发生一定的波动变化。从连铸工序的角度来考虑,当因一些不确定因素致使无法控制钢水成分稳定在某些值时,就应当从优化配水控制模型的角度出发,使二冷控制模型能更多地考虑实际生产中的一些因素,实现连铸生产过程中铸坯质量的精细控制。
2.1 新型二冷控制模型上文介绍的参数配水模型以及改进的参数配水模型考虑了拉速、过热度和二冷水温3个因素对凝固传热过程的影响,而这些配水模型中没有考虑到钢水成分变化给凝固传热过程产生的影响以及其给铸坯表面温度波动变化带来的影响。在实际生产中,每一个合格钢种成分的工艺控制要求是在某一个特定范围,实际生产中每包钢水之间除了钢水温度有一定的波动外,钢水成分也会在一定的工艺控制范围内发生波动。
表 1是某钢厂对所生产的60Si2Mn弹簧钢各成分的生产工艺控制要求以及对实际生产的200多包该钢种钢水成分的数据统计结果。由表 1可知实际生产中,同一钢种不同炉次的成分在工艺控制要求范围内会有一定的差异,钢种成分的变化直接会影响钢的一些物性参数,进而影响铸坯的凝固传热过程。钢的液、固相线温度是连铸凝固传热过程两个非常重要的物性参数,它取决于钢水中所含元素的种类、含量及其交互作用等许多复杂因素[11-12]。生产相同钢种,不同钢包钢水成分发生波动变化也会直接导致每包钢水的固、液相线温度发生变化。
| 表 1 某厂生产的60Si2Mn钢水成分的生产工艺控制要求与实际生产统计结果 |
表 2是用式(15)、式(16),根据表 160Si2Mn钢成分实际统计数据计算的相对应的钢的液相线温度和固相线温度的结果。由表 2可知,浇铸同一钢种时随着成分的变化,钢水的液、固相线温度也会发生变化,这样在相同浇注温度下,钢水的过热度也会改变,凝固区间以及凝固潜热的释放也会发生很大的变化。为此,新的模型中不仅考虑了实时变化的液相线温度,同时也考虑了凝固区间的变化给凝固传热过程带来的影响。基于此,笔者提出了新的配水模型如下:
| $ {Q_i} = {A_i}{V^2} + {B_i}V + {C_i} + {D_i}\Delta T + {E_i}\Delta {T_{{\rm{LS}}}}, $ | (7) |
| $ \Delta T = {T_{{\rm{cast}}}} - {T_{\rm{L}}}, $ | (8) |
| $ \Delta {T_{{\rm{LS}}}} = {T_{\rm{L}}} - {T_{\rm{S}}}, $ | (9) |
| 表 2 实际生产的60Si2Mn钢的固、液相线温度计算结果 |
式中:Qi为第i个冷却段的水量,L/min;V为实时拉速,m/min;ΔT为实时过热度,℃;ΔTLS为实时液、固相线温差,℃;Tcast为实时浇注温度度,℃;TL为实时液相线温度,℃;TS为实时固相线温度,℃;Ai,Bi,Ci,Di,Ei为与钢种及工况条件有关的参数,可通过建立水量计算模型及回归分析得到。
2.2 连铸凝固传热数学模型的建立笔者讨论的控制模型各参数的求解是以连铸凝固传热数学模型为基础,在建立和求解连铸坯凝固传热方程时做了以下假设:1)忽略拉坯方向的传热,凝固传热简化为二维非稳态传导传热;2)凝固坯壳的主要传热以导热为主,铸坯的液相中的对流传热等效为导热来处理,且随钢液相态的变化而变化;3)钢水的热物性参数(比热容、密度等)仅与温度、碳含量有关,用等效比热法对凝固潜热做简化处理;4)二冷区各冷却段内冷却均匀;5)铸坯内、外弧的传热条件对称。根据以上假设,铸坯的凝固传热方程简化为
| $ \rho {c_{\rm{p}}}\frac{{\partial T}}{{\partial \tau }} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right), $ | (10) |
式中:T为铸坯内被划分的网格节点温度,℃;cp为钢的比热,J/(kg·℃);λ为钢的导热系数,W/(m2·℃);τ为时间,s。
求解方程(10)的边界条件有:
| $ 结晶器:q = A - B\sqrt t , $ | (11) |
| $ 二冷区:q = h\left( {{T_{\rm{S}}} - {T_{\rm{W}}}} \right), $ | (12) |
| $ 辐射区:q = \varepsilon \sigma \left( {T_{\rm{S}}^4 - T_{\rm{O}}^4} \right)。$ | (13) |
式中:q为热流,W·m-2;TS,TW,TO分别为铸坯表面、冷却水和环境温度,℃;σ为波耳兹曼常数;ε为辐射系数,取0.80;h为传热系数,W/(m2·℃),其与水流密度的关系如下:
| $ h = A{W^n} + B, $ | (14) |
式中:A,B,n为与冷却条件有关的参数;W为水流密度,L/(m2·min)。
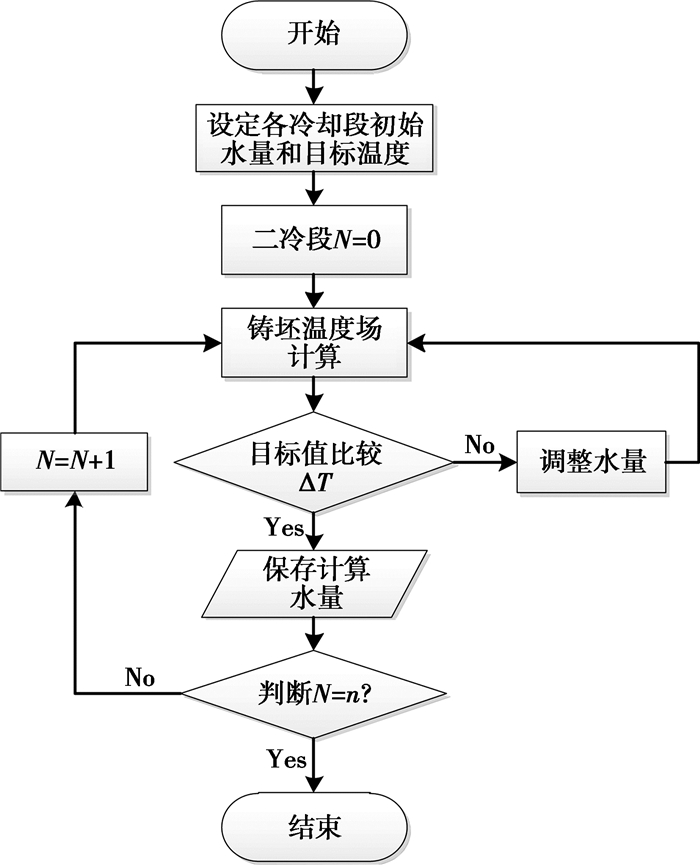
2.3 新型控制模型参数的求解求解控制模型中各参数的值是诸模型应用于生产控制的必要条件,新型二冷控制模型中的各参数Ai,Bi,Ci,Di,Ei,这5个参数的值是通过在设定目标温度下,建立各个冷却段水量与拉速、过热度以及液、固温差对应关系并通过SPSS软件回归分析得到,各工艺参数下对应的各冷却段的水量求解过程见图 1。
|
图 1 各工艺参数下二冷区各段水量的求解过程 |
如图 1所示,在凝固模型基础上,首先制定各钢种对应的各个冷却段的控制目标温度,然后再通过凝固模型计算出满足某钢种的铸坯目标表面温度的一些常用拉速、常出现的过热度以及钢种成分变化下常见的液、固相线温差工况下各冷却段的水量,在这些数据基础上,以拉速、过热度和液、固相线温差为自变量,各冷却段水量为因变量,通过SPSS软件回归分析得出各冷却段水量与拉速、过热度和液、固相线温差的函数关系,从而得出新模型的控制参数Ai,Bi,Ci,Di,Ei。
3 钢的热物性参数计算模型求解连铸凝固传热数学模型的准确性很大程度上决定于对钢水凝固过程的热物性参数的处理,笔者求解连铸凝固传热数学模型时对热物性参数按如下方式处理。
3.1 固、液相线温度计算模型求解传热凝固传热方程时,使用的钢的固相线温度计算公式见式(15)[13],液相线温度计算公式见式(16)[14],具体计算公式如下:
| $ \begin{array}{l} {T_{\rm{S}}} = 1\ 538 - \left\{ {175\left[ {\rm{C}} \right] + 20\left[ {{\rm{Si}}} \right] + 30\left[ {{\rm{Mn}}} \right] + } \right.\\ 6.5\left[ {{\rm{Cr}}} \right] + 4.7\left[ {{\rm{Ni}}} \right] + 5\left[ {{\rm{Mo}}} \right] + 4\left[ {\rm{V}} \right] + 40\left[ {{\rm{Ti}}} \right] + \\ \left. {60\left[ {{\rm{Nb}}} \right] + 7.5\left[ {{\rm{Al}}} \right] + 280\left[ {\rm{P}} \right] + 575\left[ {\rm{S}} \right]} \right\}, \end{array} $ | (15) |
| $ \begin{array}{l} {T_{\rm{L}}} = 1\ 538 + \left\{ {78\left[ {\rm{C}} \right] + 7.6\left[ {{\rm{Si}}} \right] + 4.9\left[ {{\rm{Mn}}} \right] + } \right.\\ 1.3\left[ {{\rm{Cr}}} \right] + 3.1\left[ {{\rm{Ni}}} \right] + 2\left[ {{\rm{Mo}}} \right] + 4.7\left[ {{\rm{Cu}}} \right] + 2\left[ {\rm{V}} \right] + \\ \left. {3.6\left[ {{\rm{Al}}} \right] + 34.3\left[ {\rm{P}} \right] + 38\left[ {\rm{S}} \right]} \right\}。\end{array} $ | (16) |
式中:TL为钢的液相线温度,℃;TS为钢的固相线温度,℃;[i]为元素i的质量分数,%。
3.2 其他相关热物性参数的计算模型除了固、液相线温度,钢的其他热物性参数主要包括:导热系数、比热、密度、凝固潜热等。要得到准确的计算结果,钢的热物性参数的准确与否至关重要,钢的热物性参数通常是温度和钢水成分的函数,笔者求解凝固模型中所使用的部分计算公式如下:
1) 导热系数。钢的固相导热系数主要与温度和成分有关,碳钢的固相导热系数均可用Miettinen导出的公式(17)[15]进行计算,在求解连铸凝固模型时液相区的导热系数用等效导热系数来处理,文中求解凝固传热模型时铸坯各区的导热系数具体按以下公式计算:
| $ \begin{array}{l} {\lambda _{\rm{s}}} = 20.76 - 0.009T - 3.262\ 7\left[ {\rm{C}} \right] + \left( {0.0124 - } \right.\\ 2.204 \times {10^{ - 4}}T + 1.078 \times {10^{ - 7}}{T^2} + 7.822 \times {10^{ - 4}}\left[ {{\rm{Cr}}} \right] - \\ \left. {1.741 \times {{10}^{ - 7}}T \cdot \left[ {{\rm{Cr}}} \right]} \right)\left[ {{\rm{Cr}}} \right] + \left( { - 0.586\ 0 + 8.354 \times } \right.\\ {10^{ - 4}}T - 1.368 \times {10^{ - 7}}{T^2} + 0.010\ 67\left[ {{\rm{Ni}}} \right] - 1.504 \times \\ \left. {{{10}^{ - 5}}T \cdot \left[ {{\rm{Ni}}} \right]} \right)\left[ {{\rm{Ni}}} \right] - 0.7598\left[ {{\rm{Si}}} \right] - 0.1432\left[ {{\rm{Mn}}} \right] - \\ 0.222\ 2\left[ {{\rm{Mo}}} \right]。\end{array} $ | (17) |
| $ {\lambda _{{\rm{l}},{\rm{eff}}}} = M{\lambda _{\rm{s}}}。$ | (18) |
| $ {\lambda _{{\rm{s,l}},{\rm{eff}}}} = {\lambda _{\rm{s}}}\left[ {1 + \left( {m - 1} \right){{\left( {1 - {f_{\rm{s}}}\left( T \right)} \right)}^2}} \right]。$ | (19) |
式中:λs、λl, eff、λs,l,eff分别为钢的固相区、液相区、固液两相区的导热系数,W/(m·℃);T为铸坯温度,℃;fs为钢的固相率;[i]为元素i的质量分数,%;m为有效导热系数,取值为1~5。
2) 密度。钢的高温密度主要与碳含量及温度有关,其固、液相的密度可用公式(20)、(21)[16-17]进行计算:
| $ {\rho _{\rm{s}}} = \frac{{100\left( {8\ 245.2 - 0.51\left( {T + 273} \right)} \right)}}{{\left( {100 - \left[ {\rm{C}} \right]} \right){{\left( {1 + 0.008\left[ {\rm{C}} \right]} \right)}^3}}}, $ | (20) |
| $ {\rho _{\rm{l}}} = 7\ 100 - 73\left[ {\rm{C}} \right] - \left( {0.8 - 0.9\left[ {\rm{C}} \right]} \right)\left( {T - 1\ 550} \right), $ | (21) |
| $ {\rho _{{\rm{sl}}}} = {\rho _{\rm{s}}}{f_{\rm{s}}}\left( T \right) + {\rho _{\rm{l}}}\left( {1 - {f_{\rm{s}}}\left( T \right)} \right), $ | (22) |
式中:ρs,ρl,ρsl为分别为钢的固相、液相和两相区密度,kg/m3;T为钢水温度,℃;[i]为元素i的质量分数,%;fs(T)为钢的固相率。
3) 比热和凝固潜热。铸坯凝固过程中要不断释放潜热,在连铸数值计算中,处理潜热释放的方法主要有3种:热焓法、等效比热法、温度回升法。本研究使用等效比热法,两相区的比热用有效比热来处理,相应的计算方法如下:
| $ {C_{{\rm{P}},{\rm{S}}}} = aT + b, $ | (23) |
| $ {C_{{\rm{P}},{\rm{SL}}}} = {C_{{\rm{P}},{\rm{S}}}}{f_{\rm{S}}}\left( T \right) + {C_{{\rm{P}},{\rm{L}}}}\left( {1 - {f_{\rm{S}}}\left( T \right)} \right), $ | (24) |
| $ C_{{\rm{P}},{\rm{SL}}}^E = {C_{P,SL}} + \frac{L}{{{T_{\rm{L}}} - {T_{\rm{S}}}}}。$ | (25) |
式中:CP, S、CP, SL、CP, SLE分别为固相线温度下、液相线温度下、固液两相区温度下等压比热,J/(kg·℃);CP, SLE为将凝固潜热等效到两相区比热后的等效两相区比热,J/(kg·℃);a,b为与钢种有关的系数;fS(T)为钢的固相率;T为钢水温度,℃;L为凝固潜热,J/kg。
4 结果分析与讨论本节主要讨论了常用的二冷参数配水模型(下文简称模型1,控制方程见式(3)),以及在常用的参数配水模型上改进,笔者新提出的二冷配水模型(下文简称模型2,控制方程见式(7))在钢水成分发生波动变化时的仿真结果。
4.1 模型1的计算结果分析与讨论为了便于分析讨论,本节以60Si2Mn弹簧钢为例,对表 1中实际生产钢水成分的统计数据,以成分碳的范围为主要依据,在其成分变化范围内进行等距分组,共分成6组,分组结果见表 3。用公式(15)和公式(16)计算了6组成分下的固相线温度和液相线温度,并计算了液、固相线温差,具体数值如表 4所示。通过表 4可以看出在成分发生变化时,钢的固相线温度的变化相比于液相线温度发生了更大的变化,液、固相线温差也有一定的变化,这样凝固区间也在发生变化。这说明钢水成分发生变化时会对铸坯整个凝固过程温度场的变化产生一定的影响,故如果配水模型中不考虑钢水成分的波动对凝固过程的影响,整个二冷区各冷却段末温度以及矫直点温度可能会与目标温度产生一定的偏差。
| 表 3 60Si2Mn钢的成分分组结果 |
| 表 4 60Si2Mn钢的成分分组对应的主要物性参数计算值 |
为了验证上述分析,应用文中建立铸坯凝固过程数学模型并对6组成分下的铸坯凝固传热过程进行了计算机仿真模拟,计算出上述6组成分在相同生产工况条件下的铸坯温度场。参与计算的各工艺参数以实际钢厂的生产数据为依据,主要的参数包括铸机参数和生产工艺参数,其具体数值见表 5。
| 表 5 连铸机参数和生产工艺参数 |
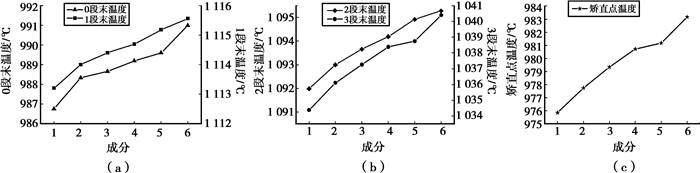
在相同的生产工艺参数下,6组成分下铸坯在每个冷却段末端以及矫直点处的铸坯表面温度的模拟结果对比趋势图如图 2所示。
|
图 2 6组成分下二冷区各冷却段末端和矫直点处铸坯表面温度的对比 |
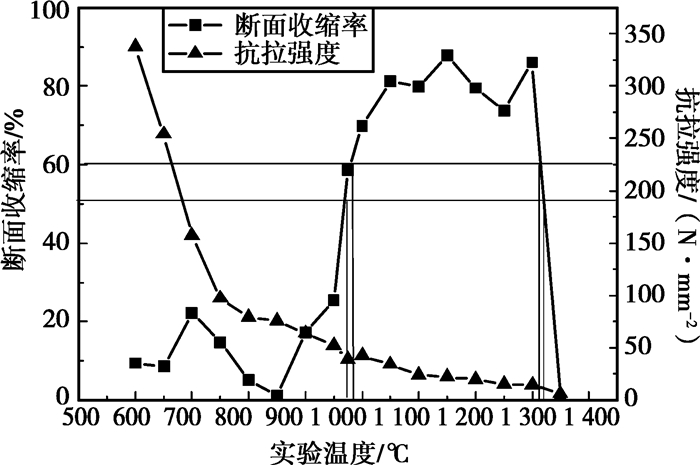
由图 2各图可以看出,相同生产工艺参数下同一钢种,其成分的波动变化会导致整个铸坯的温度场发生一定变化,而且随着冷却时间增加,这种波动变化整体趋势在增大。二冷0段末铸坯表面温度的波动变化为4.2℃,二冷1段末铸坯表面温度的波动变化为2.3℃,二冷2段末铸坯表面温度的波动变化为3.3℃,二冷3段末铸坯表面温度的波动变化为6.0℃,矫直点处铸坯表面温度的波动变化从976℃到984℃,为8.0℃。由此可以得出:除了拉速、浇铸温度会对铸坯凝固传热过程的温度场产生影响外,钢水成分的波动变化也会对其产生一定的影响。为了减少铸坯裂纹缺陷,提高铸坯的质量,对二冷段水量控制的要求有:1)整个冷却过程中铸坯表面温度的波动变化尽量小;2)控制矫直点处铸坯表面温度要避开脆性断裂区。钢种的脆性断裂区,需要通过Gleeble高温力学性能实验测得该钢种的应力-应变曲线得到。图 3所示为60Si2Mn钢的高温延塑性及强度测试结果[18]。
|
图 3 60Si2Mn钢坯断面收缩率和抗拉强度随温度变化曲线[18] |
由图 3可知60Si2Mn钢在不同温度下试样断面收缩率(R.A.)和抗拉强度随温度的变化曲线。分析曲线可以得知:在981~1316℃的温度范围内,断面收缩率(R.A.)在60%以上;当温度低于980℃时,随着温度的降低,断面收缩率(R.A.)值急剧下降,当温度降低到970℃时,断面收缩率(R.A.)值为50%,在950℃时,断面收缩率(R.A.)约为30%。由于铸坯的断面收缩率是分析评价铸坯裂纹产生的主要参数之一,对于上述6组成分,在相同冷却参数下,铸坯表面温度有的在980℃以下,有的在980℃以上,这样可能导致生产铸坯质量的不稳定性。为了保证铸坯质量的稳定性,除了要在各冷却段的铸坯温度的波动变化控制在一定的合理范围,还要着重控制矫直点处铸坯表面温度避开钢的脆性区。因此,在二冷控制模型当中考虑成分的变化对凝固过程的影响,对于精细控制铸坯质量来说很有必要。
4.2 两种模型的计算结果对比分析与讨论应用本文2.3节介绍的方法,对模型1和模型2中各参数进行回归分析求解。模型1中各参数的求解结果见表 6;模型2中各参数的求解结果见表 7。
| 表 6 模型1中各冷却段对应参数的求解值 |
| 表 7 模型2中各冷却段对应参数的求解值 |
由表 6和表 7可知两种控制模型下,对于60Si2Mn钢的每一个冷却段的水量控制方程,把这些参数存储在计算机的数据库中可以很方便地参与生产控制。表 8是对于60Si2Mn钢,在一定的生产工艺参数下(拉速为1.28 m/min,浇注温度为1 495.0℃)由两种控制模型计算得到的两种钢水成分下二冷区各个冷却段的控制水量表。
| 表 8 两种配水模型下对应水量表 |
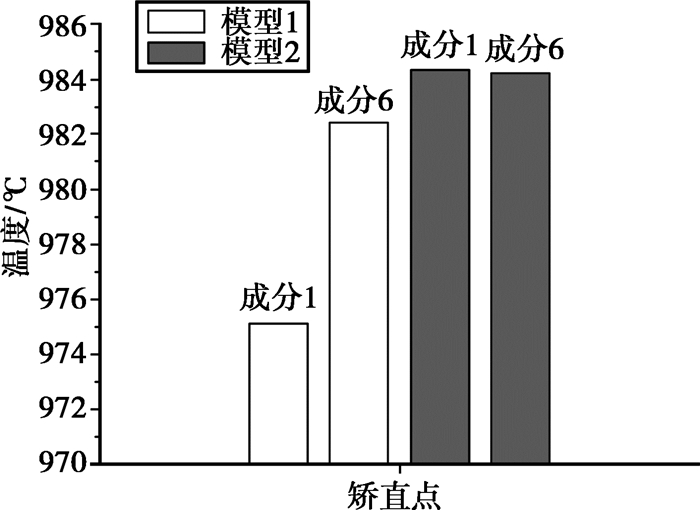
当钢水成分由成分1变化到成分6时,各冷却段的水量见表 8,应用建立的铸坯凝固传热方程对两种模型得到的不同水量下的铸坯凝固过程进行求解,得到各个冷却段末的铸坯表面温度。两种控制模型在铸坯矫直点处铸坯表面温度的模拟结果见图 4,图 5所示为在钢水成分发生波动时,应用控制模型2得到的6组成分下铸坯在矫直点处表面温度的计算结果。
|
图 4 2种控制模型在成分变化时铸坯表面温度的计算结果 |
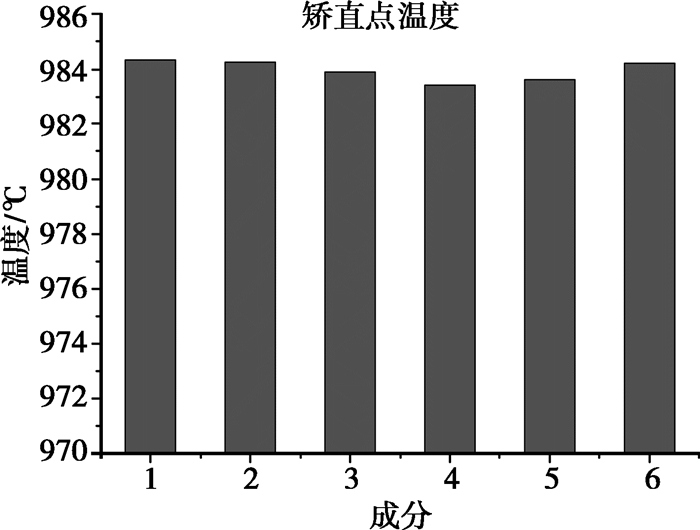
|
图 5 模型2得到6组钢水的铸坯表面温度的计算结果 |
由图 4可以得知,相同生产工艺参数(拉速和浇注温度)下,用传统的参数配水模型来控制二冷区各个冷却段的水量,当钢水成分由成分1波动变化到成分6时,矫直点处铸坯表面温度波动的差值约为7.3℃,而用新的二冷控制模型来控制二冷区水量时,两种成分的铸坯矫直点处表面温度基本不发生波动,差值仅为0.3℃,与模型1对比可知,在模型2控制下的这种波动变化降低了约95%。由图 5可知,在相同生产工艺参数(拉速和浇注温度)下,应用新型二冷制模型控制各个冷却段的水量时得到的6组成分的钢水在矫直点处铸坯表面温度能基本稳定在984℃左右,把图 5的计算结果与图 2(c)的计算结果进行对比,可知笔者新提出的二冷控制模型在钢水成分经常发生波动的情况下能更好地控制铸坯在矫直点处温度的稳定性,这样就能有效地减少因在铸坯脆性温度区间矫直而引发的各种铸坯质量问题,进而提高铸坯质量的稳定性。
5 结论1) 在传统的参数配水模型的基础上,研发了一种基于液-固相线温差补偿的连铸二冷配水控制模型,新的二冷配水控制模型不仅考虑了拉速、浇注温度对每段水量的影响,还考虑了实时的每一炉钢水成分变化对每段水量的影响。
2) 研究了两种配水模型在钢水成分发生波动的情况下对铸坯表面温度的控制影响,计算结果表明:新的二冷控制模型在成分发生波动情况下能更好地控制铸坯在矫直点处温度的稳定性。
3) 新的二冷控制模型使连铸二冷制度更加完善, 新模型对于钢水成分波动较大且经常波动的连铸生产的铸坯质量控制尤为适用。
| [1] |
刘青, 汪宙, 常健, 等.
炼钢厂的精细制造[J]. 钢铁, 2013, 48(1): 1–9, 29.
LIU Qing, WANG Zhou, CHANG Jian, et al. Fine production for steelmaking process[J]. Iron and Steel, 2013, 48(1): 1–9, 29. DOI:10.7513/j.issn.1004-7638.2013.01.001 (in Chinese) |
| [2] | Liu Q, Wang L Z, Zhang L Q, et al. Mathematical model of heat transfer for bloom continuous casting[J]. Journal of University of Science and Technology Beijing, 2008, 15(1): 17–23. DOI:10.1016/S1005-8850(08)60004-3 |
| [3] | Liu W H, Xie Z, Ji Z P, et al. Dynamic water modeling and application of billet continuous casting[J]. Journal of Iron and Steel Research International, 2008, 15(2): 14–17. DOI:10.1016/S1006-706X(08)60023-0 |
| [4] |
陈登福, 李宏亮, 牛宏波, 等.
方坯连铸二次冷却配水新模型[J]. 重庆大学学报:自然科学版, 2007, 30(6): 61–64.
CHEN Dengfu, LI Hongliang, NIU Hongbo, et al. New model for spraying water of nozzles in secondary cooling of billet continuous casting[J]. Journal of Chongqing University:Natural Science Edition, 2007, 30(6): 61–64. (in Chinese) |
| [5] | Zhang J, Chen D F, Wang S G, et al. Compensation control model of superheat and cooling water temperature for secondary cooling of continuous casting[J]. Steel Research International, 2011, 82(3): 213–221. DOI:10.1002/srin.201000148 |
| [6] |
窦志超, 张晓峰, 尹佳, 等.
基于有效拉速和有效过热度的连铸二冷控制模型[J]. 北京科技大学学报, 2011, 30(11): 1349–1353.
DOU Zhichao, ZHANG Xiaofeng, YIN Jia, et al. Secondary cooling control model based on effective-speed and effective-superheat in continuous casting[J]. Journal of University of Science and Technology Beijing, 2011, 30(11): 1349–1353. (in Chinese) |
| [7] | Dou Z C, Liu Q, Wang B, et al. Evolution of control models for secondary cooling in continuous casting process of steel[J]. Steel Research International, 2011, 82(10): 1220–1227. DOI:10.1002/srin.v82.10 |
| [8] | Hardin R A, Liu K, Beckermann C, et al. A transient simulation and dynamic spray cooling control model for continuous steel casting[J]. Metallurgical and Materials Transactions B, 2003, 34(3): 297–306. DOI:10.1007/s11663-003-0075-0 |
| [9] | Fujisaki Y, Kitada H, Sugie T. Simulator based design of secondary cooling zone control in continuous casting[J]. Tetsu-to-Hagane, 2010, 96(7): 426–433. DOI:10.2355/tetsutohagane.96.426 |
| [10] | Guo L L, Tian Y, Yao M, et al. Temperature distribution and dynamic control of secondary cooling in slab continuous casting[J]. International Journal of Minerals, Metallurgy and Materials, 2009, 16(6): 626–631. |
| [11] | Ganguly S, Choudhary S K. Quantification of the solidification microstructure in continuously-cast high-carbon steel billets[J]. Metallurgical and Materials Transactions B, 2009, 40(3): 397–404. DOI:10.1007/s11663-009-9234-2 |
| [12] | Schille J P, Guo Z L, Saunders N, et al. Modeling phase transformations and material properties critical to processing simulation of steels[J]. Materials and Manufacturing Processes, 2011, 26(1): 137–143. DOI:10.1080/10426910903153059 |
| [13] | 干勇. 现代连续铸钢实用手册[M]. 北京: 冶金工业出版社, 2010. |
| [14] | Li C S, Thomas B G. Thermomechanical finite-element model of shell behavior in continuous casting of steel[J]. Metallurgical and Materials Transactions B, 2004, 35(6): 1151–1172. DOI:10.1007/s11663-004-0071-z |
| [15] | Miettinen J. Calculation of solidification-related thermophysical properties for steels[J]. Metallurgical and Materials Transactions B, 1997, 28(2): 281–297. DOI:10.1007/s11663-997-0095-2 |
| [16] | Miettinen J, Louhenkilpi S. Calculation of thermophysical properties of carbon and low alloyed steels for modeling of solidification processes[J]. Metallurgical and Materials Transactions B, 1994, 25(6): 909–916. DOI:10.1007/BF02662773 |
| [17] | 刘旭东, 朱苗勇. 连铸凝固传热过程钢的热物性参数分析[C]//中国金属学会炼钢分会. 第十四届炼钢会议论文集. 北京: 中国金属学会炼钢分会, 2006. |
| [18] | 张建峰. 弹簧钢方坯连铸二次冷却及铸坯洁净度研究[D]. 北京: 北京科技大学, 2012. |
 2013, Vol. 36
2013, Vol. 36


