椭圆锥齿轮是非圆锥齿轮类型中一种典型的传动形式,其大端节曲线为球面椭圆。当一对椭圆锥齿轮副啮合传动时,其传动比函数具有周期性、对称性。给定匀速的输入转速,能方便地再现预先给定的非匀速输出运动。椭圆锥齿轮传动能实现两相交轴之间的非匀速比传动,相对于传统的非圆柱齿轮和圆锥齿轮的组合机构或其他组合机构,椭圆锥齿轮传动具有体积小、结构紧凑、传动效率高等优点,具有很大的应用前景[1]。
相关研究成果主要包括国外的Sentoku Hirofumi[2]给出的关于汽车差速器锥齿轮传动过程中的载荷分布和强度计算方法。国内主要有李纪强等[3]所做的关于非圆柱齿轮的啮合特性分析及承载能力研究。这些研究成果为非圆锥齿轮的设计制造及推广应用提供了理论依据和技术支撑。
随着椭圆锥齿轮传动朝着高速、动力传动的方向发展,对其传动的承载能力提出了更高的要求。文中依据微分几何理论和非圆柱齿轮的相关知识,分析了该锥齿轮传动过程中的齿面接触应力、齿根弯曲应力随主动轮转角的变化规律,以及偏心率、模数、齿数等基本参数对两种应力的影响。为判断传动过程中最薄弱轮齿的位置和齿轮基本参数的优化设计提供了理论依据,从轮齿强度的角度为椭圆锥齿轮提供了一种重要的设计分析手段。
1 椭圆锥齿轮传动原理椭圆锥齿轮啮合传动时,其共轭齿廓一直保持相切接触,瞬时啮合点不断发生变化。且主、从动轮的大端节曲线在同一个球面上做纯滚动,具有相等的球面半径,实际啮合情况如图 1所示。

|
图 1 椭圆锥齿轮副啮合传动 |
其主动轮和从动轮要实现的传动比函数[4]为
| $ {i_{12}} = \frac{{1 - 2k\cos \left( {n{\theta _1}} \right) + {k^2}}}{{1 - {k^2}}}, $ | (1) |
式中:k为椭圆锥齿轮的偏心率;n为椭圆锥齿轮的阶数;θ1为椭圆锥齿轮的主动轮转角。
当齿轮副轴间夹角为90°时,根据啮合传动时的几何关系,可得主、从动轮的节曲线为
| $ {\varphi _1} = \arctan \frac{1}{{{i_{12}}}}, $ | (2) |
| $ \left. \begin{array}{l} {\theta _2} = \int_0^{{\theta _1}} {\frac{1}{{{i_{12}}}}{\rm{d}}{\theta _1}} \\ {\varphi _2} = \frac{{\rm{ \mathsf{ π} }}}{2} - \arctan \frac{1}{{{i_{12}}}} \end{array} \right\}, $ | (3) |
式中:φ1、φ2为主、从动轮的锥角;θ2为从动轮的转角。
椭圆锥齿轮的节锥展开角为其节锥面展开到平面上所对应的中心角的大小[5]。节曲线弧长应为球面半径与节锥展开角的乘积,同时也等于节距与齿数z的乘积。依据该等式关系,可求得球面半径R为
| $ R = \frac{{180mz}}{{\int_0^{2{\rm{ \mathsf{ π} }}} {\sqrt {{{\sin }^2}\varphi \left( \theta \right) + {\varphi ^{'2}}\left( \theta \right)} {\rm{d}}\theta } }}, $ | (4) |
式中m为椭圆锥齿轮模数。
2 节曲线的平面展开及压力角计算根据微分几何曲面论的基本定理,可以将一条曲面曲线在平面上近似伸展成为平面曲线[6],其中曲线在曲面上的短程曲率kg要等于在平面上的相对曲率kr[7-8]。由Liouville公式[9]可以计算出椭圆锥齿轮副节曲线上任一点的短程曲率。
根据平面曲线相对曲率的定义,得到椭圆锥齿轮主动轮节曲线的平面展开为
| $ \left. \begin{array}{l} {\psi _1} = \int_0^\theta {\frac{{{{\varphi ''}_1}\sin {\varphi _1} - 2\varphi _1^{'2}\cos {\varphi _1} - \cos {\varphi _1}{{\sin }^2}{\varphi _1}}}{{{{\sin }^2}\varphi + \varphi _1^{'2}}}{\rm{d}}{\theta _1}} \\ x = R\int_0^\theta {{\rm{cos}}{\psi _1}\sqrt {{{\sin }^2}\varphi _1 + \varphi _1^{'2}} {\rm{d}}{\theta _1}} \\ y = R\int_0^\theta {{\rm{sin}}{\psi _1}\sqrt {{{\sin }^2}\varphi _1 + \varphi _1^{'2}} {\rm{d}}{\theta _1}} \end{array} \right\}, $ | (5) |
从动轮节曲线的平面展开为
| $ \left. \begin{array}{l} {\psi _2} = \int_0^\theta {\left( {\frac{{{{\varphi ''}_2}\sin {\varphi _1} - {{\varphi '}_1}{{\varphi '}_2}\cos {\varphi _1}}}{{\varphi _2^{'2} + {{\sin }^2}{\varphi _1}}} - \frac{{\cos {\varphi _2}}}{{{i_{12}}}}} \right){\rm{d}}{\theta _1}} \\ x = R\int_0^\theta {{\rm{cos}}{\psi _2}\sqrt {\varphi _2^{'2} + {{\sin }^2}{\varphi _1}} {\rm{d}}{\theta _1}} \\ y = - R\int_0^\theta {{\rm{sin}}{\psi _2}\sqrt {\varphi _2^{'2} + {{\sin }^2}{\varphi _1}} {\rm{d}}{\theta _1}} \end{array} \right\}, $ | (6) |
式中:ψ1为平面曲线的切向量与水平轴x的夹角;x为平面展开曲线的横轴坐标;y为平面展开曲线的纵轴坐标。
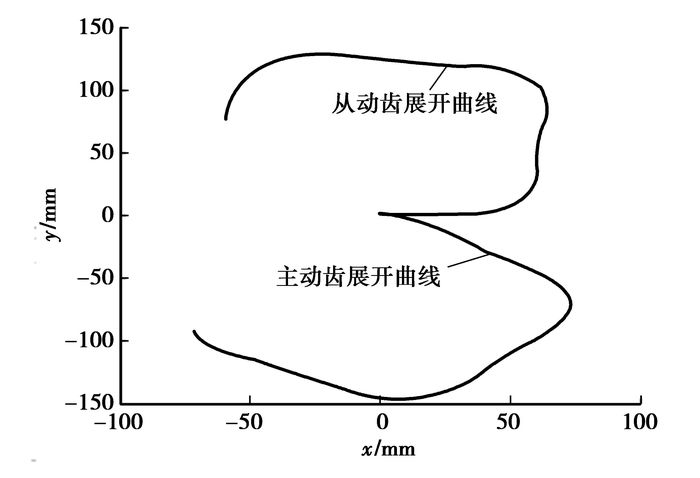
以三阶椭圆锥齿轮(m=3,k=0.15,z=33)为例,根据式(5)和式(6)得到主、从动轮节曲线的平面展开曲线如图 2所示。
|
图 2 节曲线的平面展开曲线 |
空间节曲线展开为平面当量节曲线,将椭圆锥齿轮的空间啮合问题转化成了平面啮合问题,便可以在平面当量节曲线的基础上,研究椭圆锥齿轮传动过程中的压力角变化问题。椭圆锥齿轮的压力角不等于刀具齿廓的齿形角α0(一般α0=20°),而是节曲线在某一点接触的情况[10]。当主动轮转向不同时,轮齿左右两侧齿廓的压力角不同[11]。左右两侧齿廓压力角的计算公式可统一为
| $ {\alpha _{12}} = {u_1} + {\alpha _0} - {\rm{ \mathsf{ π} }}/2, $ | (7) |
式中u1为节曲线在啮合点的切线正方向与向径之间的夹角。
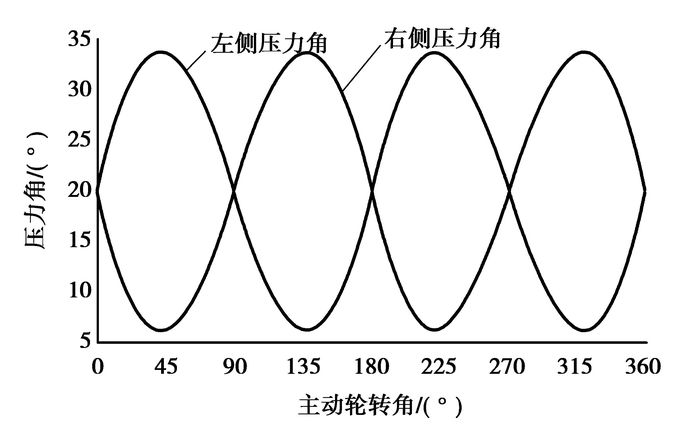
为了求出向径的方向,需要计算出当量节曲线的中心点坐标。而当量节曲线在主动轮转角等于π/n和2π/n这2点时,这2点的法线必经过当量节曲线的中心点,计算出这2点的ψ值和x、y坐标值,联立该2点的法线方程即可求出当量节曲线的中心点坐标,然后就可以计算出啮合点切线正方向与向径之间的夹角μ1。以二阶椭圆锥齿轮(m=2,k=0.1,z=22)为例,计算出传动过程中的压力角变化关系如图 3所示。
|
图 3 二阶椭圆锥齿轮传动压力角 |
齿廓形状是影响轮齿强度的重要因数,椭圆锥齿轮的齿廓形状由节曲线的曲率半径决定。从强度看,可以把椭圆锥齿轮的啮合看作是无穷多个分度圆半径等于节曲线曲率半径的直齿锥齿轮齿廓的啮合,即把节曲线视为一个连续函数,把全部的啮合点看作节点啮合来近似计算啮合过程中每个啮合点的强度。
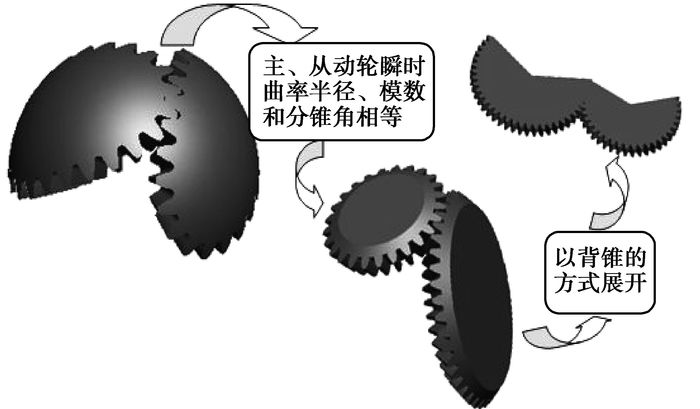
定义椭圆锥齿轮的当量齿轮是指与椭圆锥齿轮的模数相同,大端分度圆半径等于节曲线上指定点曲率半径的直齿锥齿轮,再按照背锥的方式所展开成的圆柱直齿轮,当量过程如图 4所示。当量齿轮与椭圆锥齿轮有着近似相同的齿廓,通过计算当量齿轮的强度,以一种连续的方式近似模拟节曲线上啮合点的应力状况。
|
图 4 椭圆锥齿轮的当量过程 |
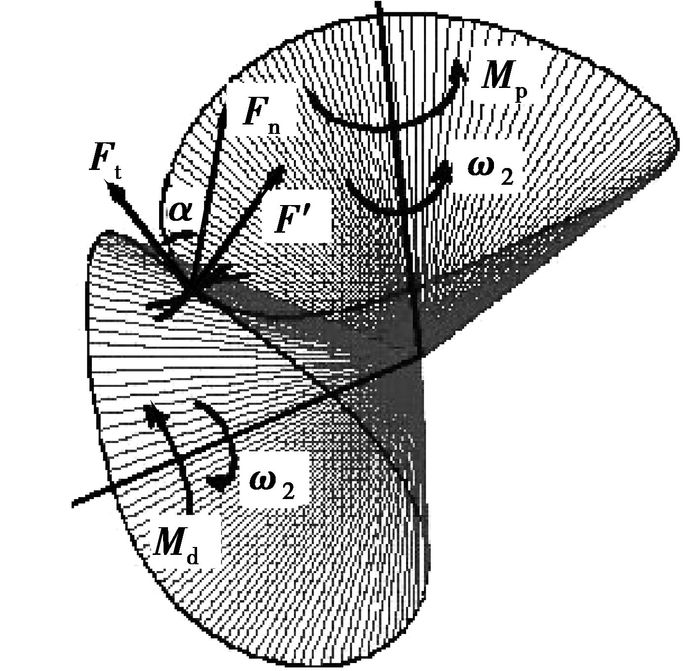
椭圆锥齿轮的运动规律已知且主动轮等速回转时(见图 5),可以确定齿轮轴上力矩之间的关系以及啮合点的受力情况为
| $ {M_{\rm{p}}} = \frac{{{M_{\rm{d}}} + {J_t}{\varepsilon _2}}}{{{i_{12}}}}, $ | (8) |
式中:Mp为有效驱动力矩;Md为有效阻力矩;Jt为从动轮的等效转动惯量;ε2为从动轮的角加速度。
|
图 5 椭圆锥齿轮受力分析 |
椭圆锥齿轮绕其回转中心轴线的转动惯量Jt为
| $ {J_t} = \rho \iiint\limits_\mathit{\Omega } {{r^4}{{\sin }^3}\varphi {\rm{d}}r{\rm{d}}\varphi {\rm{d}}\theta }。$ | (9) |
从动轮的角加速度ε2为
| $ {\varepsilon _2} = \frac{{{\rm{d}}{\omega ^2}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\left( {\frac{{{\omega _1}}}{{{i_{12}}}}} \right)}}{{{\rm{d}}t}} = - \frac{{\omega _1^2}}{{i_{12}^2}}\frac{{{\rm{d}}{i_{12}}}}{{{\rm{d}}{\theta _1}}}。$ | (10) |
将椭圆锥齿轮所承受的力矩折算到平均分度圆节曲线上,联立公式(14)~(16),得到轮齿上的切向力Ft和法向力Fn为
| $ \left. \begin{gathered} {F_t} = \frac{{{M_{\rm{d}}}\frac{{\omega _1^2}}{{i_{12}^2}}{{i'}_{12}} \cdot \rho \iiint\limits_\mathit{\Omega } {{r^4}{{\sin }^3}\varphi {\rm{d}}r{\rm{d}}\varphi {\rm{d}}\theta }}}{{R\sin \varphi \left( {1 - 0.5\frac{b}{R}} \right){i_{12}}}} \hfill \\ {F_n} = \frac{{{F_t}}}{{\cos {\alpha _{12}}}} \hfill \\ \end{gathered} \right\}, $ | (11) |
式中b为椭圆锥齿轮齿宽。
3.2 椭圆锥齿轮的齿面接触强度 3.2.1 齿面接触接触强度计算根据赫兹理论,在进行接触应力计算时,按单对齿啮合的最低点所计算所得接触应力与按节点啮合计算所得接触应力极为近似,为了计算方便,通常直接以节点啮合为代表进行齿面的接触强度计算[12-13],齿面接触应力的计算公式为
| $ {\sigma _H} = \sqrt {\frac{{{p_{{\rm{ca}}}}}}{{{\rho _\Sigma }}}} \cdot {Z_{\rm{E}}}, $ | (12) |
式中:pca为单位长度计算法向载荷;ρΣ为啮合齿面上啮合点的综合曲率半径;ZE为弹性影响系数。
| $ \frac{1}{{{\rho _\Sigma }}} = \frac{1}{{{\rho _{f1}}}} + \frac{1}{{{\rho _{f2}}}}, $ | (13) |
式中,ρf1、ρf2为啮合点处的齿形曲率半径。
在单齿啮合区,载荷由一个齿形副传递,接触线的长度就等于齿圈宽度b。啮合点处的齿形曲率半径ρf为
| $ {\rho _f} = \frac{1}{{{k_g}\cos \varphi }}\left( {1 - 0.5\frac{b}{R}} \right)\sin {\alpha _0} $ | (14) |
联立公式(12)~(14),可以计算出椭圆锥齿轮啮合过程中的齿面接触应力值。
3.2.2 基本参数对齿面接触应力的影响对于椭圆锥齿轮,其基本参数包括偏心率k,模数m和齿数z,固定其中2个参数不变,改变另外1个参数可分析该参数对齿面接触应力的影响。分析过程中设定从动轮承受有效阻力矩Md=20 N·m,主动轮转速ω1=350 r/min,载荷系数选择为使用系数ka=1.5,动载系数kv=1.1,齿间载荷分配系数kα=1.0,齿向载荷分布系数kβ=1.875(椭圆锥齿轮副使用于精密度要求不高的场合,主、从动轮均为悬臂支撑)。椭圆锥齿轮的详细参数选择如表 1所示。
| 表 1 对比过程参数选择 |
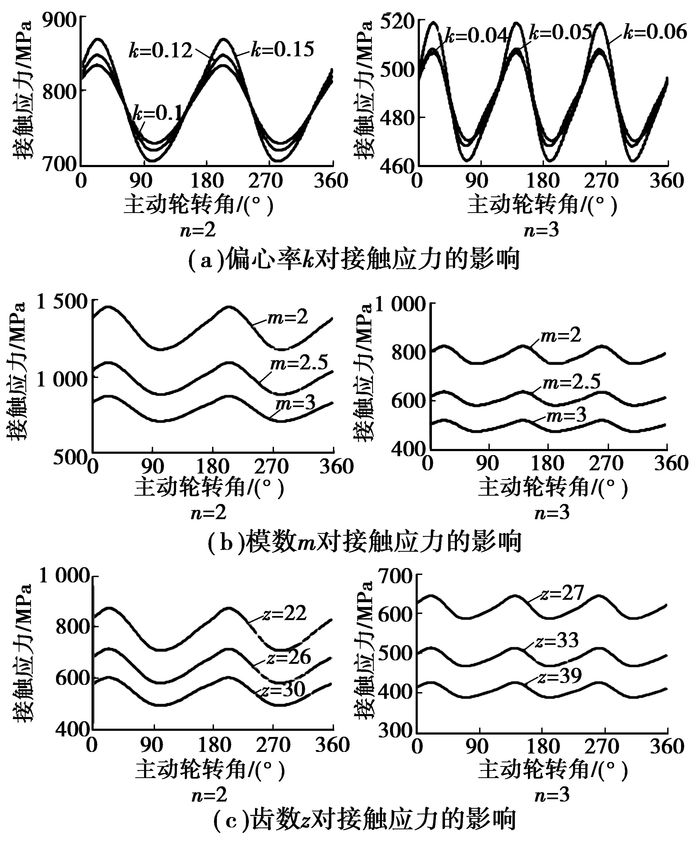
结合数学软件Matlab,以二阶和三阶椭圆锥齿轮为例,计算出椭圆锥齿轮主动轮旋转一周(假定为左侧齿廓压力角),主动轮轮齿上齿面接触应力随主动轮转角θ1的变化规律,结果如图 6所示。
|
图 6 基本参数对接触应力的影响 |
由图 6可以看出,随着主动轮转角的变化,主动轮轮齿的齿面接触应力呈周期性变化,且周期个数与阶数相同。齿面接触应力在其锥角处于中间位置时达到最大值,此时其啮合点的综合曲率半径最小。
由图 6(a)可知,随着偏心率的增大,齿面接触应力变化幅度较大,变化更加的剧烈,使主动轮在不同的转角时的齿面接触应力相差较大,在实际工程应用中有可能导致部分轮齿提前失效,因此设计过程中应该限制偏心率的大小。
由图 6(b)可知,随着模数的增大,齿面接触应力曲线近乎“等距”的减小。这主要是由于模数的增大使节曲线球面半径增大,从而减小了作用在齿面上的法向力。
齿数的增加使得节曲线的球面半径增大,减小了作用于齿廓的法向力。由图 6(c)可以看出,齿面接触应力随着齿数的增大而减小。
3.3 椭圆锥齿轮的齿根弯曲强度 3.3.1 齿根弯曲强度计算椭圆锥齿轮的齿根弯曲强度计算主要是根据其当量齿轮轮齿的悬臂梁模型计算[14]的。其最大载荷作用点的位置为单对齿啮合区上界点,危险截面则是由30°切线法确定的平截面,而齿根应力主要由弯曲应力构成[15]。
齿根弯曲应力为
| $ {\sigma _F} = \frac{{K{F_t}{Y_{F{\rm{a}}}}{Y_{{\rm{Sa}}}}}}{{bm}}, $ | (18) |
式中:K为载荷系数;YFa为齿形系数;YSa为应力校正系数。
椭圆锥齿轮的齿形系数YFa和应力校正系数YSa均以其当量齿轮的齿廓进行计算。结合数学软件Matlab,可以得到主动轮旋转1周,轮齿上齿根弯曲应力随主动轮转角的变化规律。
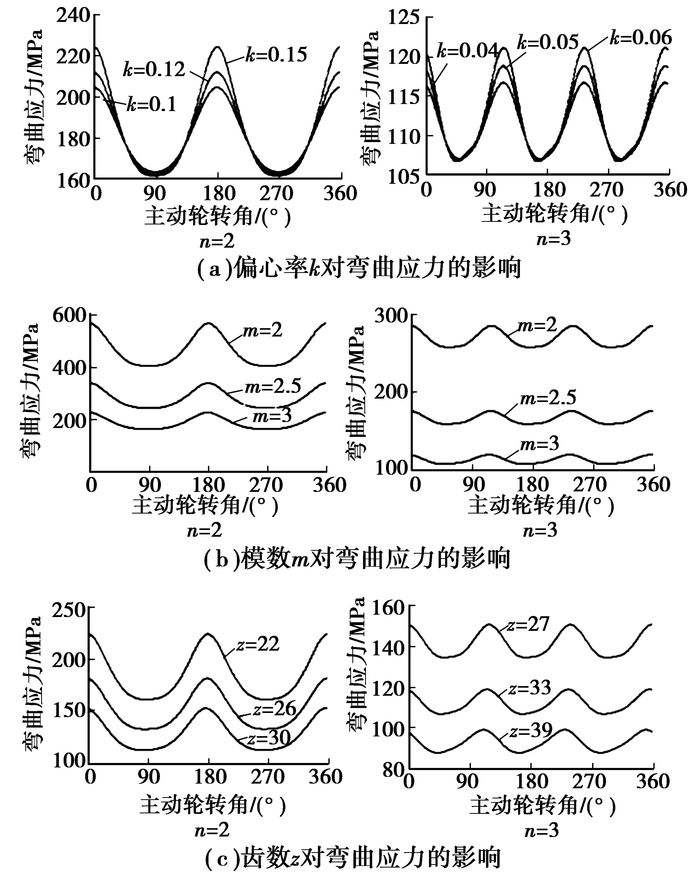
3.3.2 基本参数对齿根弯曲强度的影响分析基本参数对齿根弯曲应力的影响时,同样固定其中2个参数保持不变,改变另外1个参数分析该参数对齿根弯曲应力的影响。分析过程设定与接触应力分析时相同的主动轮转速ω1、有效阻力矩Md及载荷系数K。椭圆锥齿轮详细参数选择见表 1,计算结果如图 7所示。
|
图 7 基本参数对弯曲应力的影响 |
从图 7可以看出,随着主动轮转角的变化,齿根弯曲应力呈周期性变化,周期数与阶数相同。齿根弯曲应力值与椭圆锥齿轮锥角的变化趋势基本保持一致,即锥角越大,齿根弯曲应力值越大。
从图 7(a)可以看出,随着偏心率的增大,齿根弯曲应力的最大值以一个较大的幅度增大,而最小值减小幅度较小,即齿根弯曲应力的最大值对偏心率比较敏感,而齿根弯曲应力最小值基本不发生变化。偏心率的增大会导致不同轮齿上齿根弯曲应力相差较大,使部分轮齿提前失效。
从图 7(b)可以看出,随着模数的变化,齿根弯曲应力数值变化较大,且弯曲应力与模数成反比关系。这主要是因为模数的增大提高了齿根的抗弯曲疲劳强度,而且也使节曲线球面半径增大,减小了作用于齿廓上的切向力。
从图 7(c)可以看出,齿数的增大减小了齿根弯曲应力值。因为齿数的增加会导致节曲线球面半径的增大,在承受相同负载力矩的情况下,减小了作用于齿廓上的切向力。
4 对比分析在实际啮合过程中,节曲线上的啮合点并不是连续的,而是有限个点离散的分布在节曲线上,任意相邻2点之间的节曲线弧长等于节距。实际加工过程中,为了改善啮合过程中轮齿的受力情况,一般将锥角最大处加工成齿槽,锥角最小处加工成轮齿。因此主动轮第一个啮合点所对应的节曲线弧长为0.25p,依次往下每个啮合点对应弧长增加节距p。采用传统计算每对齿啮合强度的方法,分别计算出二阶椭圆锥齿轮(m=3,k=0.15,z=22)和三阶椭圆锥齿轮(m=3,k=0.05,z=27)主动轮每对齿节曲线上啮合点所对应的主动轮转角位置θ1、锥角φ1以及齿面弯曲应力值σF和齿根接触应力值σH,如表 2和表 3所示。
| 表 2 二阶椭圆锥齿轮节线啮合点的应力值 |
| 表 3 三阶椭圆锥齿轮节线啮合点的应力值 |
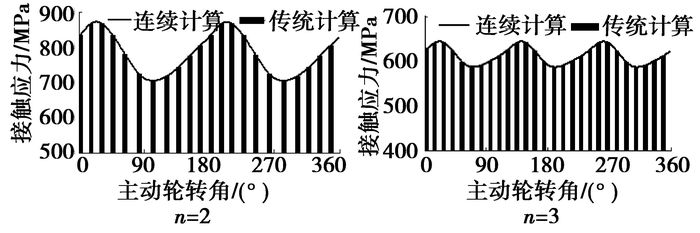
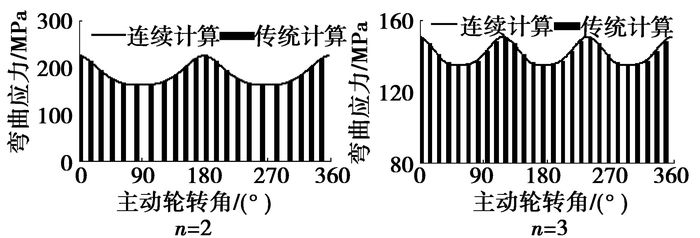
将计算出来的实际节曲线啮合点的弯曲应力、接触应力以柱状图表示,连续计算时的应力以曲线表示,如图 8和图 9所示。
|
图 8 接触应力计算对比 |
|
图 9 弯曲应力计算对比 |
从图 8和图 9可以看出,传统计算与连续计算所得的接触应力和弯曲应力值完全重合,显示出相同的规律,验证了把节曲线视为连续函数,以节点啮合为代表计算啮合过程中强度这种方法的正确性。
5 结论1) 依据微分几何原理,推导出椭圆锥齿轮的当量节曲线公式,计算出当量节曲线的中心点,得到传动过程中的压力角变化关系。
2) 通过节曲线曲率半径近似等于直齿锥齿轮的分度圆半径,把椭圆锥齿轮传动看作无穷个直齿锥齿轮啮合,建立了椭圆锥齿轮强度的连续计算方法,并用传统直齿锥齿轮强度计算法进行了对比分析,验证了连续计算方法的正确性。
3) 获得了接触应力和弯曲应力随主动轮转角的变化规律,判断了最薄弱轮齿的位置,为椭圆锥齿轮的设计、制造加工提供了便利条件。
4) 实际工程应用中,为保证所有轮齿均具有足够的强度,应限制偏心率的大小。在承受相同负载力矩的情况下,模数和齿数的增大能够有效提高轮齿强度,但同时会增大齿轮的体积与重量,为椭圆锥齿轮的安装、制造带来不利影响。
| [1] |
林超, 侯玉杰, 冉小虎, 等.
高阶椭圆锥齿轮的传动模型与干涉检查的运动仿真[J]. 重庆大学学报, 2010, 33(10): 1–6.
LIN Chao, HOU Yujie, RAN Xiaohu, et al. Transmission model of higher-order elliptical bevel gearing and motion simulation for interference checking[J]. Journal of Chongqing University, 2010, 33(10): 1–6. DOI:10.11835/j.issn.1000-582X.2010.10.001 (in Chinese) |
| [2] | Hirofumi S, Motoki T. A study of strength analysis of differential machine for a car[J]. Transactions of the Japan Society of Mechanical Engineers, 2006, 72(717): 1660–1666. DOI:10.1299/kikaic.72.1660 |
| [3] | 李纪强. 非圆齿轮传动啮合特性分析及承载能力研究[D]. 河南: 郑州机械科学研究总院, 2010. http://cdmd.cnki.com.cn/Article/CDMD-82701-2011011365.htm |
| [4] | Litvin F L. 齿轮几何学与应用理论[M]. 国楷, 叶凌云, 范琳, 等译. 上海: 上海科学技术出版社, 2008. |
| [5] | Xia J Q, Liu Y Y, Geng C M, et al. Noncircular bevel gear transmission with intersecting axes[J]. Journal of Mechanical Design, 2008, 130(5): 1–6. |
| [6] | Jia J M, Gao B, Zhao D L. Analysis method for noncircular bevel gearing based on geodesic curvature preserving mapping[J]. Chinese Journal of Mechanical Engineering, 2008, 44(4): 53–57. DOI:10.3901/JME.2008.04.053 |
| [7] |
赵玉民, 马延会, 华林, 等.
非圆锥齿轮节曲线的平面展开算法研究[J]. 中国机械工程, 2008, 19(17): 2046–2049.
ZHAO Yumin, MA Yanhui, HUA Lin, et al. Planar unfolding algorithm of noncircular bevel gears[J]. China Mechanical Engineering, 2008, 19(17): 2046–2049. DOI:10.3321/j.issn:1004-132X.2008.17.007 (in Chinese) |
| [8] |
贾巨民, 高波, 乔永卫.
越野汽车变传动比差速器的研究[J]. 汽车工程, 2003, 25(5): 498–500.
JIA Jumin, GAO Bo, QIAO Yongwei. A study on variable ratio differential for off-road vehicles[J]. Automotive Engineering, 2003, 25(5): 498–500. (in Chinese) |
| [9] | 吴大任. 微分几何学讲义[M]. 北京: 人民教育出版社, 1981. |
| [10] | Salvador C F, Netbot L J. The design of noncircular gear of constant pressure angle and the realization of its wire-electrode cutting[J]. Journal of Mechanical Design, 2007, 129(9): 981–985. DOI:10.1115/1.2748453 |
| [11] | 吴序堂, 王贵海. 非圆齿轮及非匀速比传动[M]. 北京: 机械工业出版社, 1997. |
| [12] | Fajdiga G, Flašker J, Glodež S. The influence of different parameters on surface pitting of contacting mechanical elements[J]. Engineering Fracture Mechanics, 2004, 71(4/5/6): 747–758. |
| [13] |
孙凤文, 李东峰, 付显随.
履带式装甲底盘侧减速器齿轮接触疲劳的可靠性分析[J]. 南京理工大学学报:自然科学版, 2007, 31(3): 296–299.
SUN Fengwen, LI Dongfeng, FU Xiansui. Reliability analysis of side reducer gear's contact fatigue in tracked armored vehicle[J]. Journal of Nanjing University of Science and Technology, 2007, 31(3): 296–299. (in Chinese) |
| [14] | Kramberger J, Šraml M, Potrĉ I, et al. Numerical calculation of bending fatigue life of thin-rim spur gears[J]. Engineering Fracture Mechanics, 2004, 71(4/5/6): 647–656. |
| [15] | Cavdar K, Karpat F, Babalik F C. Computer aided analysis of bending strength of involute spur gears with asymmetric profile[J]. Journal of Mechanical Design, 2005, 127(3): 477–484. DOI:10.1115/1.1866158 |
 2013, Vol. 36
2013, Vol. 36

