2. 重庆邮电大学 经济管理学院, 重庆 400065
2. College of Economics and Management, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
对于工程中的非平稳信号,采用经典的傅里叶变换已经不能得到信号中的有用信息,而时频分析是分析此类信号有力工具。常用的有短时傅里叶变换、Gabor变换和Wigner-Ville,WVD,维格纳时频分步等。对于短时傅里叶变换和Gabor变换,由于采用固定窗,使得其时间和频率分辨率难以同时得到保证,此外Gabor变换的时频聚集性不佳;WVD是一种重要的时频分析方法,具有理论上的最高时频分辨率和许多优良的数学性质;但对于多分量信号,WVD是双线性变换,不满足叠加原理,因此存在严重的交叉项干扰。目前许多学者对WVD消除交叉项干扰做了大量的研究。
笔者介绍了信号处理的基本方法[1]。PACHORI等[2]提出了采用Fourier-Besse展开先将多分量信号分解为单分量信号,再对各单分量信号分别计算WVD后合并,以达到去除交叉项的目的,纪跃波等[3]给出了CWD具体的算法实现。陈端等[4],刘文彬等[5]和MIRELA等[6]通过对多分量信号进行Gabor展开,并对各分量信号做WVD后再合成的方法避免了WVD的交叉项。PEI等[7]和KHAN等[8]提出了GWT以及改进算法,GWT结合了Gabor变换和WVD的优点。CHEN[9],MOREAU[10]和HE等[11]采用盲源分离方法对维格纳时频分布进行分解,并利用分解系数重构时频图来抑制WVD交叉项。KHANDAN等[12]使用中心仿射滤波器对信号的维格纳时频分布进行分解,并利用分解系数重构时频图来抑制WVD交叉项。
分析对比了WVD、STFT、GT以及WVD交叉项消除方法,改进了文献[13]中基于STFT的WVD的交叉项抑制方法,可以得到较GWT更好的结果。对WVD产生交叉项部分,用STFT谱幂调节项和WVD幂调节项乘积替代,通过这样的处理以达到消除交叉项的目的。
1 时频分析方法比较 1.1 WVDWVD是适用于非稳态信号处理的时频分析方法之一,与Gabor变换相比,具有更好的时频聚集性。
WVD定义为
| $ {W_x}\left( {t,f} \right) = \int_{ - \infty }^\infty {x\left( {t + \frac{\tau }{2}} \right){x^ * }\left( {t - \frac{\tau }{2}} \right){{\rm{e}}^{ - j2{\rm{ \mathsf{ π} }}f\tau }}} {\rm{d}}\tau 。$ | (1) |
WVD是一种双线性变换,不满足叠加原理。对于2个分量的信号:x(t)=x1(t)+x2(t),其WVD的结果为
| $ {W_x} = {W_{x1}} + {W_{x2}} + {W_{x1x2}} + {W_{x2x1}}。$ | (2) |
Wx1、Wx2为分量x1(t)、x2(t)的WVD,Wx1x2、Wx2x1是交叉项。WVD的交叉项是不可避免的,会严重影响区分信号项和交叉项。
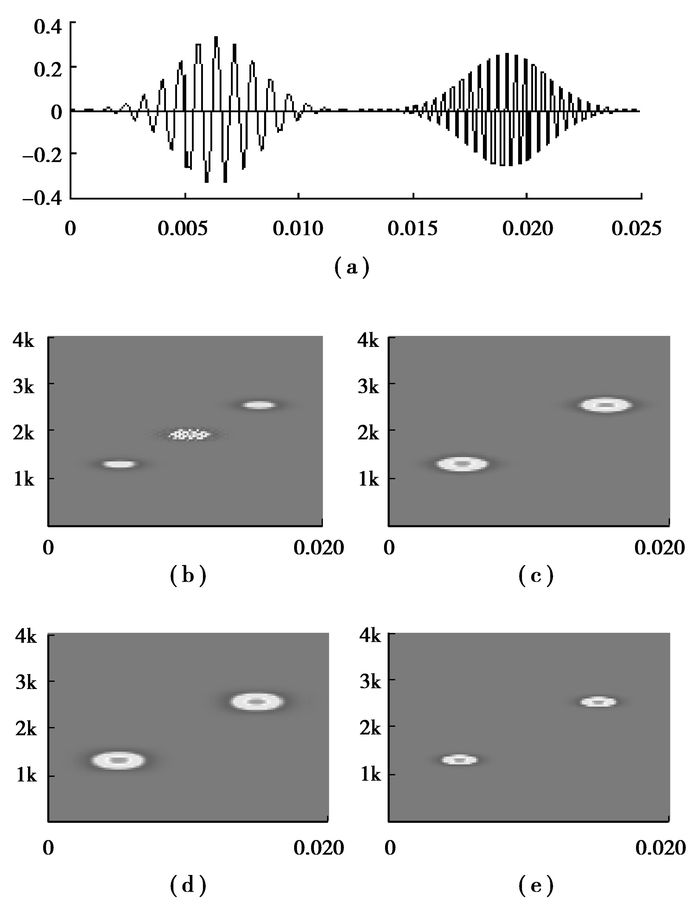
如图 1(a)所示为一时域信号,由2个不同时刻出现的非同频高斯调制信号组成,图 1(b)为该信号的WVD分布。可以看出变换结果具有明显的交叉项,并且无法分辨原分量信号和交叉项。
|
图 1 多分量信号及其时频变换 |
STFT变换定义为
| $ {\rm{SYF}}{{\rm{T}}_s}\left( {t,f} \right)\int_{ - \infty }^\infty {s\left( \tau \right){g^ * }\left( {\tau - t} \right){{\rm{e}}^{ - j2{\rm{ \mathsf{ π} }}f\tau }}} {\rm{d}}\tau , $ | (3) |
其中g(t)是一个沿时间轴滑动的时间宽度很短的函数。短时傅里叶变换可以看作是信号s(t)在分析时间t附近的傅里叶变换,通常称之为局部频谱。短时傅里叶变换信号的一种线性时频分析方法,对于多分量信号来说,它不具有交叉项。
WVD是一种二次型的变换,为了与WVD对比,在文中均使用短时傅里叶变换谱和Gabor变换谱[9]。短时傅里叶变换谱定义为STFT模的平方
| $ {S_{{\rm{STFT}}}}\left( {t,f} \right) = {\left| {\int_{ - \infty }^\infty {s\left( \tau \right){g^ * }\left( {\tau - t} \right){{\rm{e}}^{ - j2{\rm{ \mathsf{ π} }}f\tau }}} {\rm{d}}\tau } \right|^2}。$ | (4) |
图 1(c)为图 1(a)所示信号的短时傅里叶变换谱。与图 1(b)相比,可以看出短时傅里叶变换谱没有交叉项,但时频分辨率较WVD要低。
1.3 Gabor变换与Gabor变换谱Gabor变换也是信号的一种线性时频分析方法,它把时域的一维信号映射为对应的时频域二维信号,能够同时在时间和频率上表示信号的密度或强度,进而确定在某一特定的时间哪些频率存在。其处理方法是对信号x(τ)施加一个滑动窗φ(τ-t)(t是移位因子,反映滑动窗的位置)后,再作Fourier变换
| $ {G_x}\left( {t,f} \right) = \int_{ - \infty }^\infty {x\left( \tau \right)\overline {{\varphi _{t,f}}\left( \tau \right)} {\rm{d}}\tau } , $ | (5) |
其中
| $ {\varphi _{t,f}}\left( \tau \right) = \varphi \left( {\tau - t} \right){{\rm{e}}^{j2{\rm{ \mathsf{ π} }}f\tau }}, $ |
若滑动窗为高斯函数,则Gabor变换为
| $ {G_x}\left( {t,f} \right) = \int_{ - \infty }^\infty {x\left( \tau \right){{\rm{e}}^{ - {\rm{ \mathsf{ π} }}{{\left( {\tau - t} \right)}^2}}}{{\rm{e}}^{ - j2{\rm{ \mathsf{ π} }}f\tau }}{\rm{d}}\tau } 。$ | (6) |
由式(6)可以看出,Gabor变换实际是短时傅里叶变换的一种特殊形式。Gabor变换对多分量信号进行分析时,没有交叉项。
Gabor变换谱定义为
| $ {S_G}\left( {t,f} \right) = {\left| {\int_{ - \infty }^\infty {x\left( \tau \right)\overline {{\varphi _{t,f}}\left( \tau \right)} {\rm{d}}\tau } } \right|^2}。$ | (7) |
如图 1(d)所示为利用Gabor变换谱对图 1(a)所示信号进行分析,其中Gabor高斯窗长度为128。
1.4 Gabor-Wigner变换(GWT)GWT定义为2个变量Gx(t,f)、Wx(t,f)的任意函数式,表达式为
| $ {C_x}\left( {t,f} \right) = p\left( {{G_x}\left( {t,f} \right),{W_x}\left( {t,f} \right)} \right), $ | (8) |
其中p(x,y)为任意函数。例如:p(x,y)=xy,则Cx(t,f)=Gx(t,f)Wx(t,f);p(x,y)=x+y,则Cx(t,f)=Gx(t,f)+Wx(t,f)。文献[14]中定义了如下GWT变换
| $ {C_x}\left( {t,f} \right) = {G_x}\left( {t,f} \right){W_x}\left( {t,f} \right), $ | (9) |
| $ {C_x}\left( {t,f} \right) = \min \left\{ {{{\left| {{G_x}\left( {t,f} \right)} \right|}^2},\left| {{W_x}\left( {t,f} \right)} \right|} \right\}, $ | (10) |
| $ {C_x}\left( {t,f} \right) = {W_x}\left( {t,f} \right)\left\{ {\left| {{G_x}\left( {t,f} \right)} \right| > \left. {0.25} \right|} \right\}, $ | (11) |
| $ {C_x}\left( {t,f} \right) = G_x^{2.6}\left( {t,f} \right)W_x^{0.6}\left( {t,f} \right)。$ | (12) |
GWT的基本思想是通过运算,增强Gabor变换与WVD重叠部分而消弱交叉部分,这样就能够保证GWT没有交叉项的同时具有良好的时频聚集性。需注意的是GWT的计算结果只能显示时频变换后相对的大小,其幅值不能反映信号时频变换的绝对值。
图 1(e)为具有图 1(a)所示2个高斯调制分量信号的GWT变换,变换采用了公式(12)。可以看出GWT变换克服了WVD交叉项干扰,并且具有良好的时频聚集性。
Gabor变换中基函数为了保证完备性,往往采用过采样[15],过采样同时也能够提高信号Gabor展开的稳健性,但这样处理会导致Gabor变换的时频聚集性不好(ΩT<2π),当多分量信号中频率接近时,经过Gabor变换后相互干扰,此时的GWT就不能获得理想的结果。
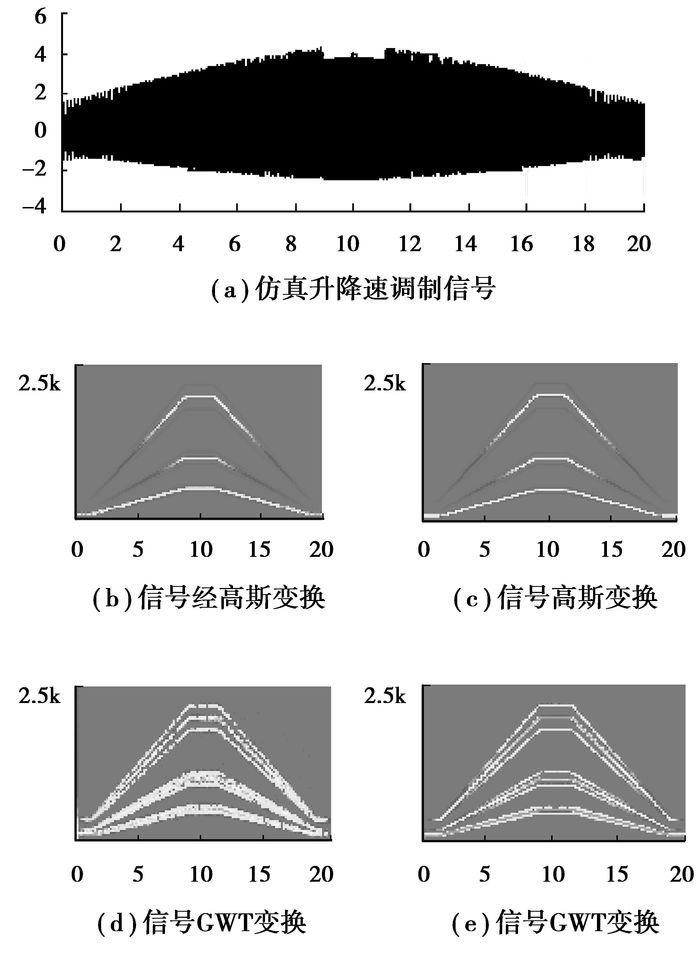
如图 2(a)所示为一仿真升降速调制信号,该信号包含3个主频率,且为2倍关系;主频率附近有调制频率。如图 2(b)所示该信号经过Gabor变换(高斯窗长度为512)后,一倍频附近的调制信号由于时频分辨率原因,完全不能分辨出主频率和调制频率;如图 2(d)所示为信号的GWT变换,由于受Gabor变换的影响,GWT也会产生同样的结果,在一倍频附近主频率和调制频率相互混叠,分辨不出主频率和调制频率。
|
图 2 升降速调制信号及其时频变换 |
为了避免GWT的缺点,这里由STFT和Wigner变换给出了STFT-Wigner变换。参照式(8)GWT的定义,STFT-Wigner变换定义为
| $ S{W_x}\left( {t,f} \right) = \min \left\{ {{S_{{\rm{STF}}{{\rm{T}}_x}}},\left| {{W_x}\left( {t,f} \right)} \right|} \right\}, $ | (13) |
| $ S{W_x}\left( {t,f} \right) = {W_x}\left( {t,f} \right)\left\{ {\left| {{S_{{\rm{STF}}{{\rm{T}}_x}}}\left( {t,f} \right)} \right| > \left. c \right|} \right\}, $ | (14) |
| $ S{W_x}\left( {t,f} \right) = {S_{{\rm{STFT}}_x^a}}\left( {t,f} \right)W_x^b\left( {t,f} \right)。$ | (15) |
式(13)为取STFT谱和WVD中数值较小者,通过这样的处理将WVD中有交叉项部分用相应STFT谱中的数值代替,以达到消除交叉项的目的。
式(14)中c为STFT谱的交叉项消除阈值。当STFT谱的值小于该阈值时,返回0;如果大于该阈值,则返回1。WVD中有交叉项对应STFT谱部分的数值肯定小于该阈值,用数字0与WVD相乘以消除交叉项。
式(15)中a、b称为幂调节系数。该式的作用是增强两变换数值较大部分而消弱有交叉项部分。随着a、b的增大,STFT-Wigner变换的时频聚集性提高。通过实验证实,a、b不易取值过高,a取值范围在1.5~3.5之间,b取值范围在0.3~1之间。
与GWT相同,STFT-Wigner变换只能显示时频变换后相对的大小,其幅值不能反映信号时频变换的绝对值。通过对仿真信号进行对比分析,式(15)所示方法较式(13)(14)结果更加理想,使用更为灵活。
如图 2(c)所示为图 2(a)中信号的STFT谱(窗函数为高斯窗,窗长度为512),图 2(c)为该信号的STFT-Wigner变换,其中a取2,b取0.5。可以看出STFT-Wigner变换能够避免交叉项干扰,并且克服了GWT中时频聚集性的问题,准确地分辨出一倍频和附近的调制频率。
3 实测实验为进一步验证算法的有效性,对一转子振动试验台进行了测试。
试验台的转子人为加了不平衡质量,使转子处于不平衡状态。ICP压电传感器布置在轴承座垂直方向,采集卡采样频率设置为5 K。调节电机转速使转子转速从0上升到3 000 r/min,记录下整个升速过程,见图 3(a)。

|
图 3 转子振动试验台振动信号及其时频分析 |
图 3(b)为采用公式(12)对信号做GWT分析结果,其中Gabor变换窗函数长度为512;图 3(c)采用公式(15)对信号做STFT-Wigner变换,窗函数为长度512的高斯窗,幂调节系数a=2,b=0.5。结果显示GWT时频分辨率明显不如STFT-Wigner变换:GWT变换中,不能够分辨出由转子不平衡引起的振动频率和50 Hz工频干扰,而STFT-Wigner变换能够准确的区分2个频率。
4 结论在计算多分量非平稳信号的时频谱时,Wigner变换存在交叉项干扰而不能得到正确的结果;并且由于Gabor变换的时频聚集性不好,同样带来分析的困难;此外Gabor-Wigner变换虽然能够避免WVD交叉项干扰问题,但不能避免Gabor变换所带来的时频聚集性差的问题。STFT-Wigner变换克服了上述问题,选择合适的窗函数以及时窗长度,通过改变幂调节系数,得到高分辨率无交叉项的时频变换。
通过仿真以及实测实验验证了STFT-Wigner变换。但STFT-Wigner变换中幂调节系数的确定没有理论基础,如何根据待分析信号的特征确定幂调节系数有待进一步研究。
| [1] | 蔡坤宝. 数字信号处理[M]. 北京: 电子工业出版社, 2007. |
| [2] | Pachori R B, Sircar P. A new technique to reduce cross terms in the wigner distribution[J]. Digital Signal Processing, 2007, 17: 466–474. DOI:10.1016/j.dsp.2006.10.004 |
| [3] |
纪跃波, 秦树人, 汤宝平.
Wigner分布干扰项抑制及其算法[J]. 重庆大学学报:自然科学版, 2001, 24(4): 26–30.
JI Yuebo, QIN Shuren, TANG Baoping. Repression of the interference in the wigner distribution and the algorithm[J]. Journal of Chongqing University:Natural Science Edition, 2001, 24(4): 26–30. (in Chinese) |
| [4] |
陈端, 刘树棠.
基于离散GABOR变换的抑制交叉项的新方法[J]. 西安交通大学学报, 1997, 31(09): 77–80.
CHEN Duan, LIU Shutang. A new method of suppressing cross terms based on discrete gabor transform[J]. Journal of Xi'An JiaoTong University, 1997, 31(09): 77–80. (in Chinese) |
| [5] |
刘文彬, 郭瑜, 李之雄.
基于Gabor展开的Wigner-Ville分布的交叉项消除[J]. 振动与冲击, 2008, 27(10): 121–123.
LIU Wenbin, GUO Yu, LI Zhixiong. Removal of crossing-items of wvd based on gabor expansion[J]. Journal of vibration and shock, 2008, 27(10): 121–123. DOI:10.3969/j.issn.1000-3835.2008.10.029 (in Chinese) |
| [6] | Mirela B, Isar A. The reduction of interference terms in the time-frequency plane[J]. Signals Circuits and Systems, 2003, 2: 461–164. |
| [7] | Pei S C, Ding J J. Relations between gabor transforms and fractional fourier transforms and their applications for signal processing[J]. IEEE Transaction on signal processing, 2007, 55(10): 4839–4841. DOI:10.1109/TSP.2007.896271 |
| [8] | Khan N A, Jaffri M N, Shah S I. Modified gabor wigner transform for crisp time frequency representation[C]. International Conference on Signal Acquisition and Processing. 2009, 2009(14):119-122. |
| [9] | Chen J. Time frequency based blind source separation technique for elimination of cross terms in wigner distribution[J]. Electronics Letters, 2003, 39(5): 475–477. DOI:10.1049/el:20030282 |
| [10] | Moreau E. A generalization of joint-diagonalization criteria for source separation[J]. IEEE Transactions on Signal Processing, 2001, 49(3): 530–541. DOI:10.1109/78.905873 |
| [11] | He Z Y, Yang L X, Liu J. Blind source separation using clustering-based multivariate density estimation algorithm[J]. IEEE Transactions on Signal Processing, 2000, 48(2): 575–579. DOI:10.1109/78.823988 |
| [12] | Khandan F, Ayatollahi A. Performance region of center affine filter for liminating of interference terms of discrete wigner distribution[J]. Image and Signal Processing and Analysis, 2003(2): 621–625. |
| [13] |
吕宙.
基于STFT的Wigner-Ville分布交叉项抑制[J]. 航天电子对抗, 2010, 26(3): 27–29.
LV Zhou. Cross-terms suppression in wigner-ville distribution based on STFT[J]. Aerospace Electronic Warfare, 2010, 26(3): 27–29. (in Chinese) |
| [14] | Qian S E, Chen D P. Joint time-frequency analysis[J]. Signal Processing Magazine IEEE, 1999, 16(2): 52–67. DOI:10.1109/79.752051 |
| [15] | 张贤达, 保铮. 非平稳信号分析与处理[M]. 北京: 国防工业出版社, 1998. |
 2013, Vol. 36
2013, Vol. 36


