振动主动控制系统包括一个或者多个控制源,通过次级通道引入主动控制力来抑制或削弱基础结构振动[1]。由于振动主动控制具有效果好、适应性强等优点,已成为国内外振动工程界的研究热点。振动主动控制系统的核心部分是控制算法,控制算法的选择是否恰当直接关系到最终的控制效果,目前存在多种控制方法,其中基于自适应滤波的主动对消是常用的方法[2],方法本身具有较好的自适应能力,对模型参数的变化并不敏感,而且能够获得较好的控制效果[3-4]。自适应滤波控制算法主要包括FxLMS(filtered-x least mean square)算法,递推最小二乘法(RLS)和快速横向滤波算法(FTF)[5]等,其中FxLMS是振动和噪声主动控制领域最受欢迎的自适应控制算法[6],这是因为:1)无论控制目标是宽带还是窄带都能根据实际情况进行结构调整来适应环境;2)易于描述和理解,尤其是算法本身只有乘/加运算,其运算结构易与标准DSP硬件匹配;3)存在物理建模误差和有限计算精度的截断误差时鲁棒性好[7-8]。
目前对FxLMS算法研究多侧重于算法自身特性研究和结构改进方面的理论研究。Kuo等[9]分析了窄带有源噪声控制中FxLMS算法的收敛条件,通过设定理论边界对算法进行优化,提高了算法的收敛速度。Hansen等[10]研究了影响单输入单输出时域FxLMS算法控制输出的3个因素,并提出了相应解决方案。Ardekani等[11]从理论上推导了FxLMS算法的收敛条件,建立了预测FxLMS算法收敛特性的新模型,仿真结果验证了该收敛条件的正确性。J. Duan[12]为了抑制传动系统引起的车内噪声,应用频域FxLMS算法并进行了变形,仿真结果对比显示改进算法的优越性,并未用于实车实验。Hinamoto等[13]对FxLMS算法进行了改进并应用在多频段的有源噪声控制仿真中,结果显示在迭代开始时速度明显加快。然而以上研究很少涉及算法在实际应用中的问题,而算法的实现是其从理论到实际工程应用的关键环节。在准确把握算法结构的基础上,文中采用Level-2 S函数设计了自定义通用FxLMS模块,在Simulink环境中实现了FxLMS算法,并将该模块应用在齿轮传动系统振动主动控制试验台进行硬件在环仿真验证。由于采用Level-2 S函数编写的算法模块支持更多的应用程序接口,可以通过Simulink Coder(2011年之前的Matlab版本称为Real-Time Workshop)自动生成可执行代码,也可以通过dSPACE的软件TargetLink直接生成产品级代码,为后续的硬件实验研究和实际工程应用提供了便利。
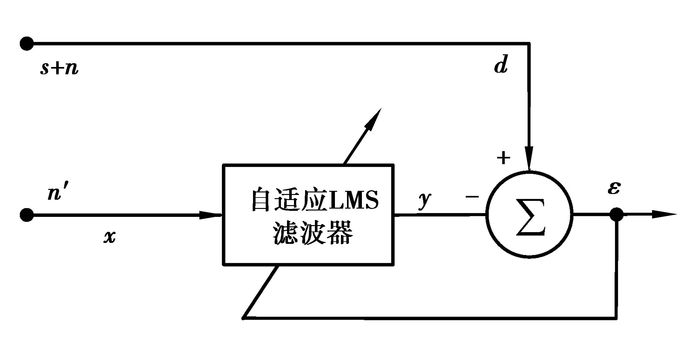
1 FxLMS算法结构FxLMS算法是最小均方(LMS)算法在振动和噪声主动控制实际应用中的一种改进。基于误差梯度估计的LMS算法被广泛应用于电噪声干扰对消系统中[14](见图 1),信号s受到噪声n的污染,如果能够得到一个与n相关的噪声n′可以利用,那么就可以用一个自适应LMS滤波器产生一个与n尽可能相像的输出y,因此总输出ε将逼近s,从而消除了噪声。
|
图 1 自适应LMS干扰对消 |
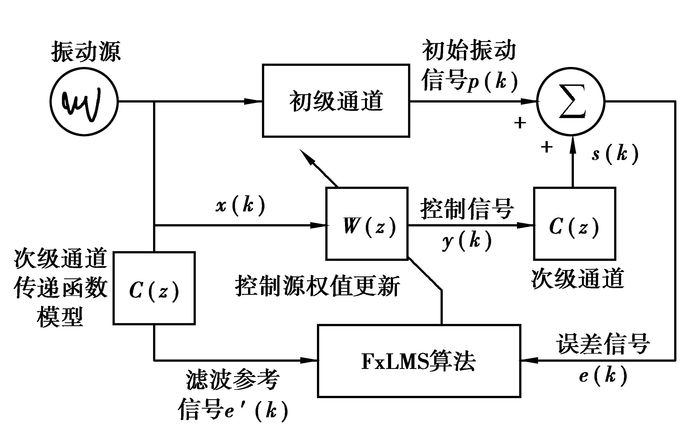
而噪声和振动的主动控制不同于电噪声对消系统,其控制器输出不是直接与初级噪声相加,而首先要通过电声/振装置(扬声器/作动器)转换成次级声音/振动信号,用以抵消初始的振动和噪声;经过一定的传播延迟,再把初、次级声/振作用完成抵消干涉后的残余振动噪声经过声/振电装置(误差传感器)转换成电信号,才得到误差信号。从扬声器、作动器等执行机构到误差传感器之间的通路称为次级通道。次级通道的存在,使误差梯度的瞬时测量值不再是真实的梯度的无偏估计。为保证LMS算法的收敛,引入1个模拟次级通道的模型对参考输入信号x(n)进行滤波,把滤波后的参考信号x′(n)与误差e(n)的乘积作为误差梯度的估计值,所获得经修正的LMS算法就称为FxLMS算法。图 2是采用FxLMS算法的振动主动控制系统框图。
|
图 2 应用FxLMS算法振动主动控制系统 |
控制系统的功能有效地分为2部分:控制信号的计算和控制滤波器的权值更新。误差信号e(k)为初始振动源信号p(k)与控制源产生的反振动信号s(k)之和:
| $e\left( k \right) = p\left( k \right) + s\left( k \right)。$ | (1) |
在k时刻,N阶FIR控制滤波器的输出y(k)等于卷积运算
| $\begin{array}{l} y\left( k \right) = \sum\limits_{i = 0}^{N - 1} {{w_i}} \left( k \right)x\left( {k - i} \right)\\ \quad \quad = {w^{\rm{T}}}\left( k \right)x\left( k \right) = {x^{\rm{T}}}\left( k \right)w\left( k \right)。\end{array}$ | (2) |
如前所述,FIR控制滤波器得到的前馈控制信号y(k)将不等于误差信号的控制源成分s(k),因此需要次级通道在这2种状态下进行转换,在仿真中,次级通道的传递函数在时域内可以用m阶FIR滤波器来建模
| $c = {[{c_0}{c_1}, \ldots ,{c_{m - 1}}]^{\rm{T}}}。$ | (3) |
控制通道产生的反振动成分s(k)等于LMS滤波器与次级通道传递函数的卷积为
| $s\left( k \right) = y\left( k \right) \cdot c = \sum\limits_{i = 0}^{m - 1} {w\left( k \right)} x\left( {k - i} \right){c_i} = {y^{\rm{T}}}\left( k \right)c,$ | (4) |
式中y(k)是控制滤波器输出的一个m×1阶矢量,
| $y\left( k \right) = {x^{\rm{T}}}\left( k \right)w,$ | (5) |
式中x(k)是控制滤波器的输入。
控制滤波器中用来自适应加权函数的梯度下降算法
| $w\left( {k + 1} \right) = w\left( k \right) - 2\mu e\left( k \right)f\left( k \right),$ | (6) |
式中f(k)是滤波后的参考信号向量。
| $f\left( k \right) = {x^{\rm{T}}}\left( k \right)c。$ | (7) |
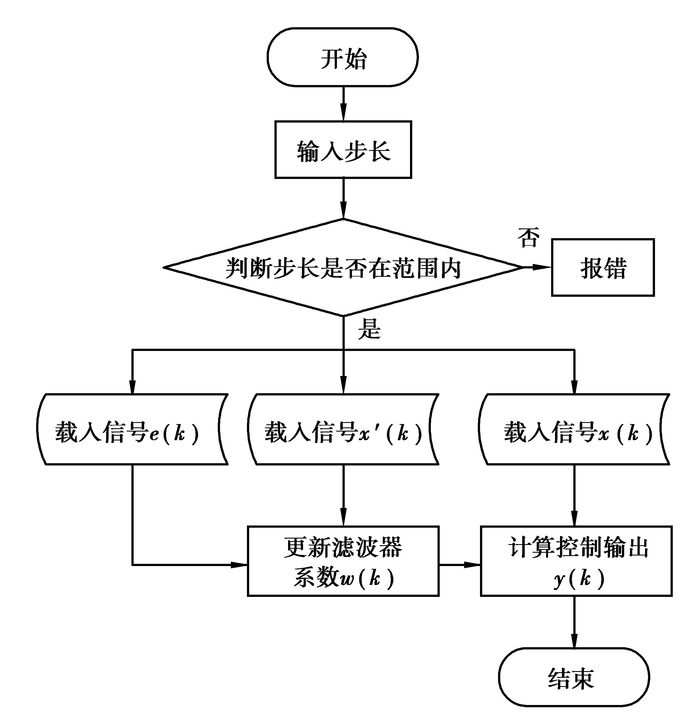
式(6)是FxLMS算法的权值迭代推导公式,在实际的算法应用中,已知输入信号x(k)、次级通道传输函数c以及误差信号e(k),取权值w的初值为0,就可以按照以上公式设计算法程序,流程图如图 3所示。
|
图 3 FxLMS算法流程图 |
Matlab/Simulink提供了信号处理工具箱(DSP System Toolbox)进行数字信号处理系统设计、仿真与分析,其中包含了各种类型的LMS自适应滤波器,但没有FxLMS算法模块,LMS算法和FxLMS算法在误差信号的获取以及权值迭代算法结构的不同也导致FxLMS算法不能用LMS滤波器模块来实现,为了在Simulink环境中实现基于FxLMS算法的振动主动控制仿真,采用Level-2 S函数自定义FxLMS通用模块,S函数代码可以用M语言编写,也可以是C、C++、Ada、Fortran等语言编写。其中M文件型S函数分为2种:Level 1型和Level 2型,Level-1 M文件型S函数形式简单,运行速度快,但无法处理复数数据以及基于帧的数据,采用Level-2 S函数设计FxLMS模块,主要基于以下考虑。
1) FxLMS为典型的多输入多输出算法,Level-2 S函数具有支持多输入多输出的优势。
2) Level-2 S函数编写的代码和C-MEX S函数的回调方法类似,并且应用程序接口也相互对应,方便转换成高效C代码。
3) Level-2 S函数支持Dwork向量,Dwork向量是Simulink为S函数的每次调用分配的存储模块,不同于全局变量和静态变量,Dwork向量在数据进行多次调用时有专门的存储空间,可以避免迭代数据被覆盖。
4) 通过相应的目标语言编译器(TLC),Level-2 S函数编写的模块可以直接生成目标C代码,可以直接下载到dSPACE或DSP处理器里进行验证以及工程实际应用。
Level-2 S函数的应用程序接口(API)定义了组成S函数所需要的回调方法(Callback Method)的信号和基本功能。这些API的实现决定了模块的属性(端口、参数和状态等)和行为(模块作为模块输入、状态和参数的函数的输出)。通过实现一组回调方法就可以建立满足需求的模块类型,文中在建立FxLMS模块时用到了以下回调方法。
1) Setup函数体,执行模块初始化,Setup函数体是Level-2 S函数模块必须的,构建FxLMS模块过程中,Setup函数执行的任务包括3类。①参考信号、滤波后参考信号和误差信号3个输入端口,以及控制信号和权值迭代系数2个输出信号端口;②设置端口的维数、数据类型、复杂性和采样时间等属性:维数均为1维,数据类型为双精度类型,复杂性为实数,采样时间为继承(inherit);③设置对话的参数个数并检验参数的有效性。对话参数为步长μ。通过S-function模块的运行时对象的RegBlockMethod方法,将各个模块方法注册到所用的本地M文件中的函数。
2) CheckPrms函数体,用于检验对话参数μ的合法性。当对话参数超出了规定的数值范围,程序将给出错误提示。
3) DoPostPropSetup函数体,建立2个Dwork向量,分别为“x”变量(参考信号迭代),“w”(权值迭代),设置变量的初始属性,用于数据更新。如果自建的S函数模块存在多次调用,那么必须采用Dwork向量,而不能采用全局或静态变量。
4) Start函数体,设置Dwork向量的初值为0。
5) Outputs函数体,按照FxLMS算法的流程计算更新滤波器输出和权值迭代,并将计算结果送给输出端口。
通过上述Level-2 S函数的回调方法完成了FxLMS算法模块在Simulink中的建立。
3 离线仿真验证为对自建FxLMS算法模块进行验证,现将用Level-2 S函数建立的FxLMS模块应用在一离线主动控制算例中进行仿真。如图 4所示,图中阴影部分为自建FxLMS模块。取激励源为80 Hz、95 Hz和110 Hz幅值均为1的3个正弦信号与高斯白噪声信号叠加作为初始振动信号,初级通道、次级通道均采用FIR滤波器模拟,控制滤波器的阶数为80,FxLMS步长为对话参数μ,设定μ值为0.001,采样时间为0.000 1 s。

|
图 4 FxLMS模块用于振动主动控制Simulink仿真结构 |
设定初级通道传递函数[15]为
| $\begin{array}{l} p\left( z \right) = 0.001 + 0.005{z^{ - 1}} - 0.005{z^{ - 2}} + 0.75{z^{ - 3}} + \\ \quad \quad \quad 0.5{z^{ - 4}} - 0.35{z^{ - 5}} - 0.4{z^{ - 6}} + 0.2{z^{ - 7}} - \\ \quad \quad \quad 0.4{z^{ - 8}} - 0.1{z^{ - 9}}, \end{array}$ |
次级通道传递函数为
| $c\left( z \right) = 0.01 + 0.01{z^{ - 1}} + 0.9{z^{ - 2}} - 001{z^{ - 3}} - 0.75{z^{ - 5}}。$ |
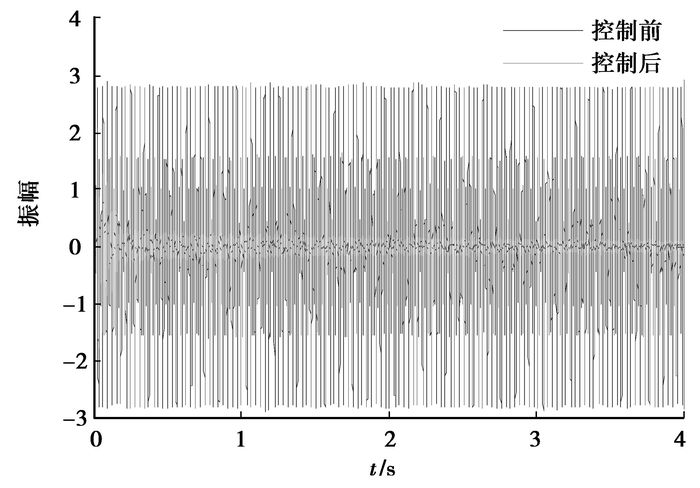
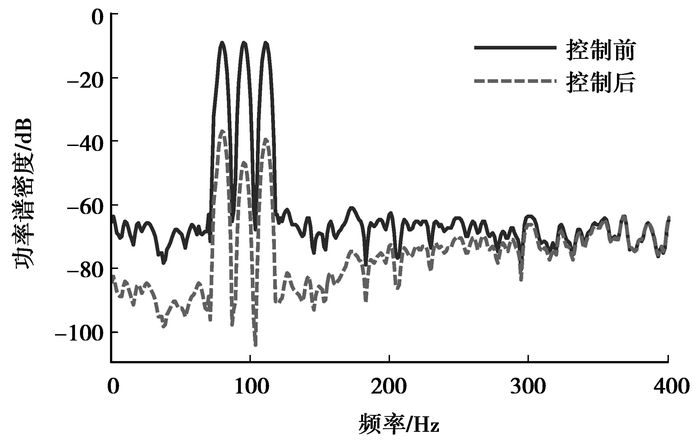
图 5为振动主动控制的时域仿真结果,在理想情况下(参考信号与待消除振动信号完全相同,次级通道的估计与实际的次级通道完全相同),初始振动信号几乎完全被抑制,并在1 s左右时间达到收敛稳定。图 6为振动信号在控制前后的频域图,可以看出,被控振动信号在频域表现为分立的线谱,经过主动控制后,线谱位置没有发生变化,但是幅值代表的能量值大大减弱。图 7为滤波器的权值w在时域内迭代更新曲线,权值w的个数等于滤波器的阶数。如果振动源为稳定的周期谐波信号,权值经过多次迭代后最终趋于稳定。
|
图 5 振动信号主动控制时域结果 |
|
图 6 振动信号经主动控制前后频域图 |

|
图 7 权值(w)迭代 |
在FxLMS算法中,若控制系统外部结构固定,那么影响其性能的参数主要有2个:滤波器权值更新步长μ和自适应滤波器的阶数n,文献[10]指出FxLMS算法收敛时步长的取值范围为
| ${\mu _{{\rm{max}}}} \approx \frac{2}{{{p_{x\prime }}L}},$ | (8) |
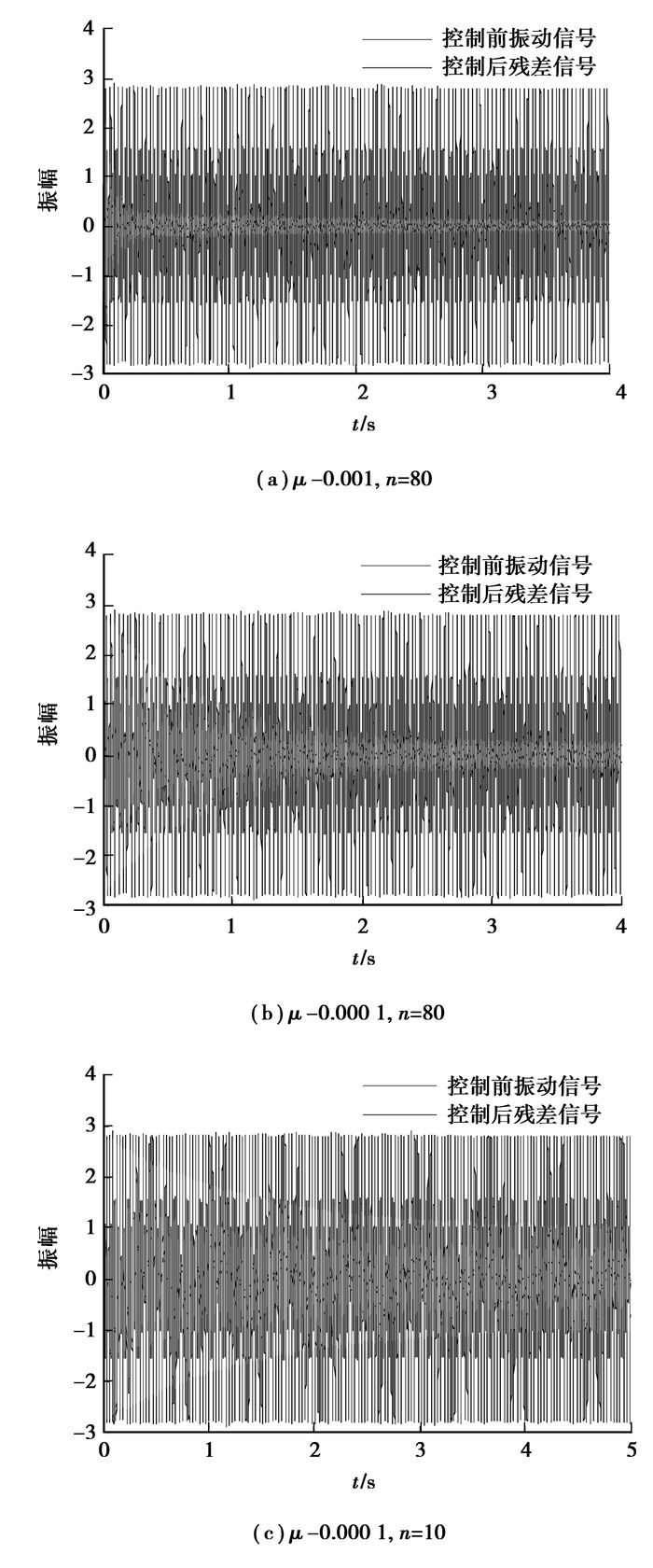
式中,px′是滤波后参考信号的功率谱,L代表滤波器的阶数,而事实上次级通道的响应是动态的,动态的自适应使式(8)给的最大收敛步长分析不再准确有效。为了验证所建FxLMS模块的性能,在保证稳定的前提下,分别改变滤波器的步长μ和阶数n,得到仿真结果。首先研究滤波器的步长对算法性能的影响,保持滤波器的阶数80不变,设定对话参数—权值迭代步长μ,为0.001和0.000 1,分别得到仿真结果,见图 8(a)和图 8(b)。可以看出,当μ减小时,收敛速度明显变慢。然后保持步长为0.000 1不变,分别取控制滤波器的阶数为80和10,得到仿真结果见图 8(b)和图 8(c)。不难看出,当阶数n减少时,其频率的控制带宽也会变小,如果不能完全覆盖被控信号的频带,将会有部分频带的振动不能消除,图 8(c)中,控制后的残余振动信号明显比图 8(b)的大。
|
图 8 不同参数后主动控制结果 |
FxLMS算法与LMS算法本质上是一致的,都是梯度最速下降寻优的算法,因此参数对性能的影响相近:在系统收敛的前提下,增大步长μ会加速收敛,减少阶数n时,计算量必然变小,同时也减弱了控制的效果。上面的结果也反映出相同的规律,对算法的性能分析也验证了自建FxLMS模块的正确性。
5 硬件在环仿真将该算法模块应用于齿轮传动系统的振动主动控制中,进一步验证所建FxLMS模块的正确性并探讨用于齿轮传动系统振动主动控制的可行性。在搭建的功率流开放式实验平台上,构建了齿轮箱与压电作动器、控制器、信号采集器构成的振动主动控制硬件在环仿真系统,如图 9所示。

|
图 9 齿轮传动系统振动主动控制试验平台 注:1.dSPACE DS1103单板系统;2.PC机;3.电荷放大器;4.LMS测试仿真系统;5.功率放大器;6.扭矩测量仪;7.电流加载控制仪;8.测功机;9.调速器;10.振动加速度传感器;11.压电作动器;12.齿轮传动系统;13.调速电机 |
通过Simulink中Simulink Coder和DSpace的RTI模块,将FxLMS算法从模块生成代码并下载到DSpace中用做控制器,并配置I/O端口与试验台的硬件进行连接。其中对压电作动器的动作进行控制的FxLMS控制器是振动主动控制的核心部分,包含3个输入,2个输出。其中3个输入的获取对算法的实现和结果起关键作用,分别进行如下设置。
1) 参考信号x(k),参考信号的获取,由固定在轴上的加速度传感器经过滤波后,在经过频率估计和波形重建得到。参考信号在进行频率估计的时候,只选取了振幅最大的啮合基频信号。
2) 滤波后参考信号x′(n)。参考信号经过次级通道进行滤波。根据FxLMS算法的特性,次级通道的建模不必非常准确,如果次级通道模型的冲激响应和次级通道本身具有一样大的传输延迟,那么FxLMS算法仍然稳定收敛,因此在实验中将次级通道的模型简化增益和延迟的组合,进一步简化了算法并提高了算法效率。
3) 误差信号e(n),误差信号为经过控制后齿轮传动系统的残余振动分量,仍然由轴上的加速度传感器信号获取,在经过电荷放大器进行放大时也进行了硬件滤波处理。由于在误差信号中仍然有其他干扰信号的存在,对控制结果有一定影响。
2个输出分别为控制输出y(n)和权值更新输出w(n)。控制器的输出信号直接作用在压电作动器的电压源用来驱动作动器的动作。
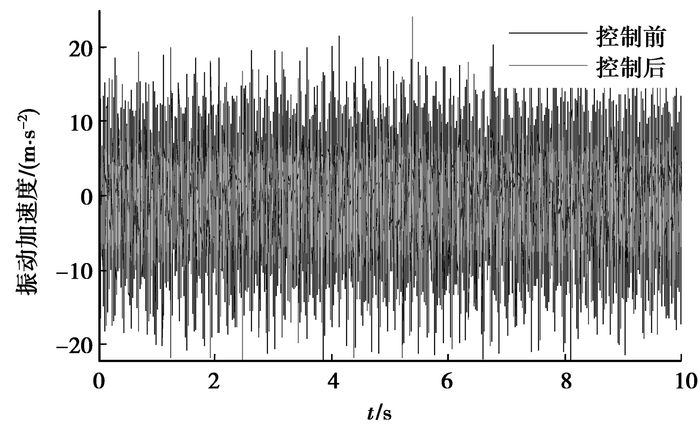
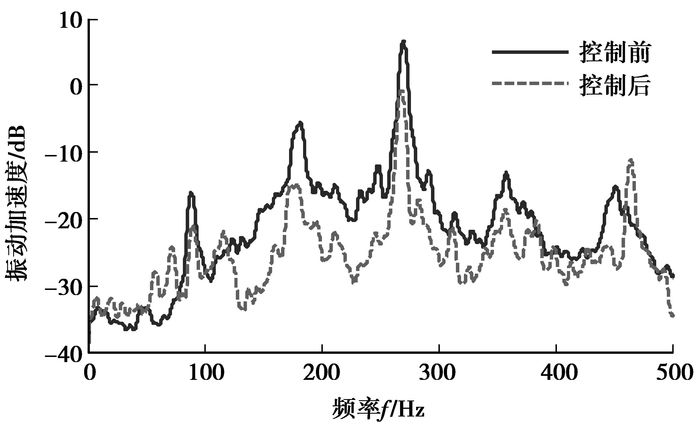
通过dSPACE软件组件ControlDesk可以方便的进行采集数据、修改变量等操作,利用LMS Test.Lab测控系统进行信号采集与实时监测。在转速为432 r/min(齿频270 Hz),负载为1 N·m的工况下得到控制结果,图 10为施加控制前后的时域振幅变化情况,可以看出控制后的齿轮振动加速度振幅有明显减弱,图 11为齿轮传动系统在运行时,轴上的振动在控制前后的频域结果,可以看出经过主动控制后,齿轮轴上的振动在齿轮啮合频率处(270 Hz)有6.9 dB的衰减。
|
图 10 齿轮振动主动控制时域结果 |
|
图 11 啮合频率为270 Hz时频域控制结果 |
从FxLMS算法结构出发,实现了FxLMS算法在Simulink里面的构建,并利用该模块对FxLMS算法的性能进行了分析。将控制算法代码下载到dSPACE中作为控制器,与内置压电作动器的齿轮主动结构组成硬件在环系统进行实验验证。结果表明:在Matlab/Simulink环境下利用Level-2 S函数设计自定义模块来实现FxLMS算法是正确可行的;通过dSPACE硬件在环仿真验证,FxLMS算法是解决振动主动控制问题的一个可靠有效的算法。
| [1] | Elliott S. Signal processing for active control[M]. London: Academic Press, 2000. |
| [2] | Hillis A J, Harrison A J L, Stoten D P. A comparison of two adaptive algorithms for the control of active engine mounts[J]. Journal of Sound and Vibration, 2005, 286(1/2): 37–54. |
| [3] |
赵剑, 徐健, 李晓东, 等.
基于多模型的自适应有源噪声控制算法研究[J]. 振动工程学报, 2007, 20(6): 549–555.
ZHAO Jian, XU Jian, LI Xiaodong, et al. An adaptive active noise control algorithm using multiple models[J]. Journal of Vibration Engineering, 2007, 20(6): 549–555. (in Chinese) |
| [4] | Carnahan J J, Richards C M. A modification to filtered-X LMS control for airfoil vibration and flutter suppression[J]. Journal of Vibration and Control, 2008, 14(6): 831–848. DOI:10.1177/1077546307084240 |
| [5] |
梁青, 段小帅, 陈绍青, 等.
基于滤波x-LMS算法的磁悬浮隔振器控制研究[J]. 振动与冲击, 2010, 29(7): 201–203.
LIANG Qing, DUAN Xiaoshuai, CHEN Shaoqing, et al. Control of electromagnetic suspension vibration isolator based on filtered x-LMS algorithm[J]. Journal of Vibration and Shock, 2010, 29(7): 201–203. (in Chinese) |
| [6] | Vicente L, Masgrau E. Novel FxLMS convergence condition with deterministic reference[J]. IEEE Transactions on Signal Processing, 2006, 54(10): 3768–3774. DOI:10.1109/TSP.2006.880205 |
| [7] | Lopes P A C, Piedade M S. The behavior of the modified FX-LMS algorithm with secondary path modeling errors[J]. IEEE Signal Processing Letters, 2004, 11(2): 148–151. DOI:10.1109/LSP.2003.821745 |
| [8] | Kuo S M, Tahernehadi M, Hao W G. Convergence analysis of narrow-band active noise control system[J]. IEEE Transactions on Circuits and System Ⅱ:Analog and Digital Signal Processing, 1999, 46(2): 220–223. DOI:10.1109/82.752958 |
| [9] | Qiu X J, Hansen C H. A study of time-domain FXLMS algorithms with control output constraint[J]. Journal of the Acoustical Society of America, 2001, 109(6): 2815–2823. DOI:10.1121/1.1367247 |
| [10] | Ardekani I T, Abdulla W H. Theoretical convergence analysis of FxLMS algorithm[J]. Signal Processing, 2010, 90(12): 3046–3055. DOI:10.1016/j.sigpro.2010.05.009 |
| [11] | Duan J, Li M F, Lim T C, et al. Active control of vehicle transient powertrain noise using a twin-FxLMS algorithm[J]. Journal of Dynamic Systems, Measurement, and Control, 2011, 133(3): 1–4. |
| [12] | Hinamoto Y, Sakai H. Analysis of the filtered-X LMS algorithm and a related new algorithm for active control of multitonal noise[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2006, 14(1): 123–130. DOI:10.1109/TSA.2005.854089 |
| [13] | Xiao Y G, Ma L Y, Hasegawa K. Properties of FXLMS-Based narrowband active noise control with online secondary-path modeling[J]. IEEE Transactions on Signal Processing, 2009, 57(8): 2931–2949. DOI:10.1109/TSP.2009.2020766 |
| [14] | WidrowB, StearnsS D. 自适应信号处理:英文版[M]. 北京: 机械工业出版社, 2008. |
| [15] |
张晓宇, 仪垂杰.
次级通道在线辨识的神经网络方法[J]. 噪声与振动控制, 2009, 29(1): 69–72.
ZHANG Xiaoyu, YI Chuijie. Neural network method for online secondary path identification[J]. Noise and Vibration Control, 2009, 29(1): 69–72. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

