2. 重庆邮电大学 经济管理学院, 重庆 400065;
3. 重庆交通大学 管理学院, 重庆 400074
2. College of Economics and Management, Chongqing University of Posts and Telecom munications, Chongqing 400065, China;
3. School of Management, Chongqing Jiaotong University, Chongqing 400074, China
车辆调度问题(Vehicle routing problem,VRP)是运筹学中一个重要的研究热点,广泛应用与交通运输、智能控制和信息技术等不同领域,由于其具有重要的理论和应用价值,吸引众多学者从不同方面对其进行研究。
车辆调度问题最早由Dantzig于1959年提出,经过半个多世纪的发展,在数学建模和求解算法方面已取得众多研究成果。如Ma,H等[1]研究了带时间窗约束和路段容量限制的车辆调度问题;Erdogan,S等[2]提出了绿色车辆调度问题的概念;Ribeiro,GM等[3]研究了累计容量限制的车辆调度问题;张景玲[4]研究多车型的动态车辆调度问题;张建勇[5]研究模糊需求信息条件下的实时动态车辆调度问题;吴斌[6]研究了开放式动态网络的车辆调度问题。由于车辆调度问题属于NP-Hard问题,其求解算法一直是困扰车辆调度问题的一个难点,目前已有的研究成果主要是利用启发式算法对其求解,如赵燕伟等[7]设计了量子遗传算法;李兵[8]设计了遗传算法;陈火根等[9]设计了遗传算法与禁忌算法相结合的混合算法;郎茂祥等[10]设计了爬山算法与遗传算法相结合的混合算法;Clara Novoa[11]研究了动态车辆调度问题求解问题,并得出它没有全局最优解的结论;Rodrigo Moretti Branchini[12]提出了局部搜索算法;Juliane Müller[13]提出动态带有时间窗车辆调度问题的次优解算法。由文献分析可知,已有的车辆调度问题的求解算法,在求解效率和稳定性上存在不同程度的缺陷。
在综合分析现有文献的基础上,根据车辆调度问题的特点,设计自然数编码的染色体结构,并利用云模型云滴的随机性和稳定倾向性改进自适应遗传算法中交叉率和变异率设置方式,设计云自适应遗传算法对有约束的车辆调度问题求解。最后,结合算例对模型和算法的有效性进行验证。
1 建立以综合费用为优化目标的车辆调度模型 1.1 优化目标选择车辆调度问题的优化目标选择是研究多车型车辆调度问题的关键,已有的文献对多以运输距离最短为优化目标,而没有考虑运输量和车载率。如:文献[14]以配送车辆的总吨位公里数最少为优化目标;文献[15]以笼统的总收益为优化目标,没有对车辆使用成本进行细分;文献[16]以车辆的运输距离最短和发车成本最小直接相加之和为优化目标;文献[17]以租赁成本和可变成本之和最小,为优化目标没有考虑车载率对可变成本的影响;文献[18]分别对以距离成本和油耗成本为优化目标展开研究,但其没有考虑不同车型的固定使用成本的不同。为此,提出以车辆的固定使用成本和可变成本为优化目标,其中:固定成本为购买车辆的成本和司机的工资和福利成本,或租赁成本;可变成本为与行驶距离和车载率相关的油耗成本。
在运输路径中第i段运输距离中,用pi表示车辆的实载率,qi表示车辆的实际载重,Q表示最大车载量,则车辆的实载率可以表示为:
| $ {{e'}_i} = {e_1} + {p_i}\left( {{e_2} - {e_1}} \right)。$ | (1) |
若已知运输距离为si,由(1)可以得到第i段运输距离中的总油耗成本为
| $ C = {s_i}\left[ {{e_1} + {p_i}\left( {{e_2} - {e_1}} \right)} \right] = {e_1}{s_i} + {s_i}{p_i}\left( {{e_2} - {e_1}} \right)。$ | (2) |
根据配送网络中客户的需求量和车载量,可预先估计完成任务所需要的车辆数m为
| $ m = \left[ {\frac{{\sum\limits_{i = 1}^L {{q_i}} }}{{\partial Q}}} \right] + 1, $ | (3) |
式中:[·]表示取整;L表示客户数量;0<∂<1,是车容量的装载系数,与装车的复杂性程度及约束限制有关。
建立以车辆固定使用费用和配送油耗成本最小为优化目标的多车型车辆调度模型,首先给出决策变量为
| $ {x_{ijk}} = \left\{ \begin{array}{l} 1,车辆\;k\;由客户\;i\;驶向客户\;j;\\ 0,其他。\end{array} \right. $ |
| $ {y_{ik}} = \left\{ \begin{array}{l} 1,客户\;i\;的配送任务由车辆\;k\;完成;\\ 0,其他。\end{array} \right. $ |
则可以建立如下数学模型:
| $ \begin{array}{*{20}{c}} {{Z_{\min }} = \sum\limits_{i = 0}^L {\sum\limits_{j = 0}^L {\sum\limits_{k = 1}^m {{c_{ij}}{x_{ijk}}{e_1}} } } + }\\ {\sum\limits_{i = 0}^L {\sum\limits_{j = 0}^L {\sum\limits_{k = 1}^m {{c_{ij}}{x_{ijk}}{p_{ijk}}\left( {{e_2} - {e_1}} \right)} } } + \sum\limits_{k = 1}^m {{y_{0k}}F} ;} \end{array} $ | (4) |
| $ {\rm{ST}}:{p_{ijk}} = \frac{{\left( {\sum\limits_{j = 1}^L {{q_j}{y_{ik}}} - \sum\limits_{i = 1}^{j - 1} {{q_i}{y_{ik}}} } \right)}}{Q}; $ | (5) |
| $ \sum\limits_{j = 1}^L {{q_j}{y_{ik}}} \le Q,k = 1,2, \cdots ,m; $ | (6) |
| $ \sum\limits_{k = 1}^m {{y_{ik}} = 1} ,i = 1,2, \cdots ,L; $ | (7) |
| $ \sum\limits_{j = 1}^L {{x_{0jk}} = m} ; $ | (8) |
| $ \sum\limits_{i = 1}^L {{x_{ijk}} = {y_{ik}}} ,j = 1,2, \cdots ,L,k = 1,2, \cdots ,m; $ | (9) |
| $ \sum\limits_{j = 1}^L {{x_{ijk}} = {y_{ik}}} ,i = 1,2, \cdots ,L,k = 1,2, \cdots ,m; $ | (10) |
| $ {x_{ijk}} = \left( {{x_{ijk}} - 1} \right) = 0; $ | (11) |
| $ {y_{ik}} = \left( {{y_{ik}} - 1} \right) = 0; $ | (12) |
| $ X = \left( {{x_{ijkr}}} \right) \in S。$ | (13) |
式中:0表示车场;cij表示第i个客户到第j个客户的距离(文中采用2点之间的直线距离);pijk表示车辆k从第i个客户到第j个客户间的实载率;F表示车辆的固定使用费用;Q表示车辆的标准装载量;qi表示第i个客户的需求量;S为支路消去约束集。
式(4)表示配送总费用最小的目标函数;式(5)表示车辆k在客户i到客户j间的实载率;式(6)表示车辆不能超载;式(7)表示每个客户只能由1台车辆完成;式(8)表示配送中心发出的车辆应满足客户的配送需求;式(9)和式(10)表示2个变量之间的关系;式(11)和式(12)表示为0~1的变量;式(13)表示消去构成不完整线路的行车路径。
2 云自适应遗传算法 2.1 云模型理论概念自1995年李德毅院士[20]提出“隶属云与语言原子模型”等概念以来,云理论得到不断发展,内容不断丰富,逐步完善形成了云模型理论。云模型是模糊理论的创新与发展,实现了定型概念与定量数值之间的不确定转换,并成功地应用于智能控制和数据挖掘等不同领域。
云概念的整体性通过云模型的3个数字特征来反映,期望(Expected value,Ex)是云滴在论域空间分布的数学期望,表示定性概念的点;熵(Entropy,En)是定性概念的不确定性度量,由云滴的随机性和模糊性共同决定,分别反映云滴的离散程度和可接受云滴的取值范围。超熵(Hyper entropy,He)是熵En的度量,即熵的熵。云模型是云滴的具体实现过程,也即是定性概念向定量转换的过程,此过程称为云发生器。一维正态云滴的生成算法如表 1所示。
| 表 1 算法1:一维正态云模型的生成 |
遗传算法(Genetic algorithm,GA)是借鉴生物进化中“适者生存”自然规律的特征,随机产生可行性解,并通过一定的机制进行选择、交叉和变异操作,产生最优解或近似最优解的随机优化算法。标准遗传算法(Static genetic algorithm,SGA)在交叉和变异操作算子中采用确定性的固定概率进行,算法存在未进化至最优解时已经收敛或者收敛的速度太慢,使算法的实际应用不强。
云自适应遗传算法(Cloud adaptive genetic algorithm,CAGA)是利用云模型中云滴随机性和稳定倾向性的特点设计遗传算法中交叉概率Pc和变异概率Pm,在算法的初期采用较大的交叉概率和变异概率,使集中在适应度低的个体以较大的概率参与交叉和变异操作,产生优秀个体,在算法的后期采用较小的交叉概率和变异概率,使集中在适应度高的优秀个体以较小的概率参与交叉变异,保护优秀个体不被破坏,加速算法的全局寻优能力。
在此,由云模型X条件发生器算法生成遗传算法的交叉概率和变异概率,具体生成算法如表 2所示。
| 表 2 算法2:自适应交叉概率Pc和变异概率Pm的生成 |
设计云遗传算法,具体如下。
1) 染色体编码:针对车辆调度问题的特点设计自然数的染色体编码结构,如(0,i1,i2,…,ie,0,if,…,ik,0,…,0,ip,…,iL,0),长度为L+m+1,其中,ij表示某条线路上第j个需求客户,0表示配送中心。
2) 初始化种群:随机产生客户的全排列,并在首尾处插入0,根据约束条件在中间插入m-1个0,重复此步骤,产生P个数目的种群个数。
3) 适应度函数:设计fitness(x)=M-fit(x),其中,fit(x)是车辆行驶总费用,也即目标函数值;M=10 000。
4) 选择算子:设计赌盘选择算子,首先,计算种群中每个个体在种群中的相对适应度,并进行排序。其次,根据其适应度对赌盘进行划分,将每个个体划分为不同的扇形。如此,优秀的染色体得到相对较多的机会进入下一代。
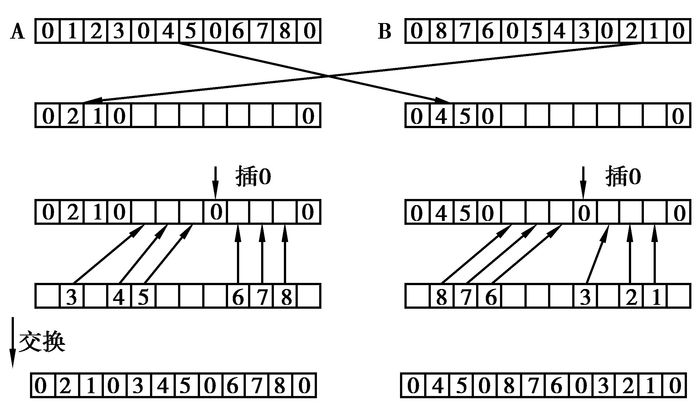
5) 最大保留交叉算子:根据车辆调度问题染色体编码组间无序组内有序的特点,设计交叉算子选择交叉点时,选择在0的位置,当交叉点不是0时,选择最近的0位置作为交叉点。具体操作如图 1所示。
|
图 1 最大保留交叉算法 |
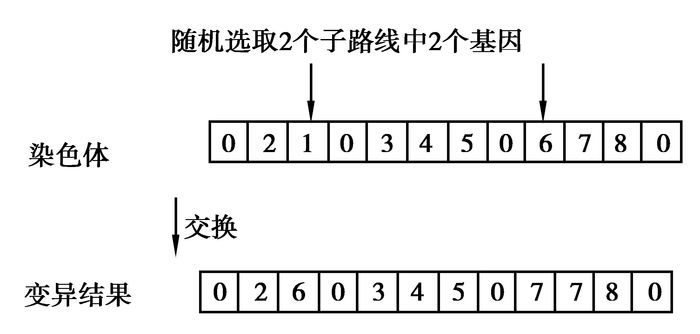
6) 变异算子:随机选择2个非0编码,交换其位置,产生新染色体,具体如图 2所示。
|
图 2 变异算法 |
重复步骤2)至6),当T=100或maxfitness-minfitness=0时,终止循环,输出结果。
2.3 性能参数设置正态云是一种泛正态分布,呈中间大两头小的状态特点,期望Ex和熵En分别影响云模型的水平位置和陡峭程度,超熵He和云滴的离散程度成正比。所有云滴均在期望值附近波动,波动的程度由He控制。根据“3En”规则可知,En越大云覆盖的范围也就越大,从而是个体在交叉和变异操作时搜索空间也越大。结合算法的收敛速度和求解精度,在云遗传算法中可取C1=C3=6p(p为初始种群的大小),并且随进化代数逐渐增大,在此设置C1=C3=6p(T+1)(T为进化代数)。由于He决定云滴离散程度,当He过大时,云模型在一定程度上丧失稳定倾向性,而当He过小时,云模型又会丧失随机性。为了算法运行初期扩大搜索空间,运行后期提高搜索精度,He可以先大后小的设置,如
研究由软件Maple1 3.0随机产生30个客户的配送网络对模型和算法进行实验验证,配送车辆载重量为8 t,没有最大行驶距离限制,固定使用费用为100元/次,空载油耗为0.56元/(km·t),满载时油耗为:1.58元/(km·t),配送中心坐标O(50 km,50 km),客户的坐标及货物需求量见表 3。文中采用直线距离,根据坐标位置进行计算。
| 表 3 客户需求信息 |
根据配送网络中客户的需求量和车载量,估计完成任务所需要的车辆数为
| $ m = \left[ {\frac{{\sum\limits_{i = 1}^L {{q_i}} }}{{\partial Q}}} \right] + 1 = 7。$ |
由2.2节的算法对车辆调度模型进行求解,计算结果如表 4所示。
| 表 4 配送总费用最小的车辆调度方案 |
由表 4可以得出结论:车辆调度若以配送距离最短和载重为有效约束,优化出来的行车路径最短,但实际上其消耗的油耗成本却比较高,综合考虑运输距离和车载量对油耗费用的影响,以总的配送成本为优化目标更为科学合理。
3.2 算法对比分析为了检验云遗传算法的求解性能,在此,分别采用标准遗传算法[21]、禁忌搜索算法[21]和云自适应遗传算法对上算例进行实验,收敛状况如图 3所示。

|
图 3 算法收敛对比图 |
由图可见,禁忌搜索算法的收敛速度最快,云自适应遗传算法次之,但其收敛下降速度是最快的,反映出其全局收敛能力比较强。
为了检验算法的鲁棒性,对上算例计算20次,分别对最优值、最劣值、平均值等计算指标进行统计,如表 5所示。
| 表 5 仿真结果对比分析 |
通过表 5看出,3种算法搜索成功率从大到小依次为云自适应遗传算法、标准遗传算法、禁忌搜索算法,最劣值、平均值从小到大依次为云自适应遗传算法、标准遗传算法、禁忌搜索算法,反映出云自适应遗传算法的全局搜索能力最强,标准遗传算法次之,禁忌搜索算法最弱。3种算法平均成功搜索并收敛代数从小到大依次为禁忌搜索算法、云自适应遗传算法、标准遗传算法。可见云自适应遗传算法在保证快速收敛的同时而且没有降低全局搜索能力。
3.3 标准化测试分析从车辆调度问题网站(http://neo.lcc.uma.es/radio/WebVRP/)上下载关于有约束车辆调度问题的标准算例,车辆参数与3.1相同。分别采用标准遗传算法[21]、禁忌搜索算法[21]和云自适应遗传算法进行求解,并对每个实例均随运行20次,统计最优解、均值和与最优解的误差(见表 6),分析算法的求解效率和稳定性。
| 表 6 测试数据统计结果 |
由表中可见,3种算法求解结果均与已知最优解存在误差,但云自适应遗传算法比标准遗传算法和禁忌搜索算法得出更优解。对于小规模的车辆调度问题,3种算法均能计算出比较好的解,但是随着规模的增大,标准遗传算法和禁忌搜索算法的稳定性就开始下降,而云自适应遗传算法却依然能够取得较好的结果,这得益于云自适应遗传算法中动态改变的交叉变异率,使算法的初期能够比较快地产生优秀个体,算法的后期保护最优个体,全局搜索能力强。
试验表明:文中设计的云自适应遗传算法在全局搜索和快速收敛方面优于其他智能算法,能够保证大规模车辆调度问题对求解算法的要求。
4 结论1) 研究了有能力约束的车辆调度问题,并建立以油耗费用和固定费用最小为优化目标的数学模型,该模型考虑了车辆的实载率和运输距离与油耗之间的关系,改进了以往以运输距离最短为优化目标,忽略运输量和车辆利用率2个与运输成本非常重要的影响因素。
2) 设计云自适应遗传算法求解车辆调度问题,改进标准遗传算法中固定交叉和变异概率,利用云模型云滴的随机性和稳定倾向性设计自适应遗传算法中交叉率和变异率,在算法的初期设置较大的交叉和变异概率,快速产生优秀个体,在算法的后期设置较小的交叉和变异概率,保护优秀基因被破坏。设计最大保留机制的交叉算子,避免优秀基因被破坏。
3) 最后,结合算例对设计的算法进行了实验计算,结果表明,云自适应遗传算法在求解效率、收敛速度和稳定性方面优于其他智能算法。
| [1] | Ma H, Cheang B, Lim A, et al. An investigation into the vehicle routing problem with time windows and link capacity constraints[J]. Omega, 2011, 40(3): 336–347. |
| [2] | Erdoǧan S, Miller-Hooks E. A green vehicle routing problem[J]. Transportation Research Part E:Logistics and Transportation Review, 2011, 48(1): 100–114. |
| [3] | Ribeiro G M, Laporte G. An adaptive large neighborhood search heuristic for the cumulative capacitated vehicle routing problem[J]. Computers and Operations Research, 2011, 39(3): 728–735. |
| [4] |
张景玲, 赵燕伟, 王海燕, 等.
多车型动态需求车辆路径优化问题建模及优化[J]. 计算机集成制造系统, 2010, 16(3): 543–550.
ZHANG Jingling, ZHAO Yanwei, WANG Haiyan, et al. Modeling and algorithms for a dynamic multi-vehicle routing problem with cusormers' dynamic requests[J]. Computer Integrated Manufacturing Systems, 2010, 16(3): 543–550. (in Chinese) |
| [5] |
张建勇, 李军, 郭耀煌.
模糊需求信息条件下的实时动态车辆调度问题研究[J]. 管理工程学报, 2004, 18(4): 69–72.
ZHANG Jianyong, LI Jun, GUO Yaohuang. Research of the fuzzy dynamic vehicle scheduling problem when demand at nodes is uncertain[J]. Journal of Industrial Engineering and Engineering Management, 2004, 18(4): 69–72. (in Chinese) |
| [6] |
吴斌, 倪卫红, 樊树海, 等.
开放式动态网络车辆路径问题的粒子群算法[J]. 计算机集成制造系统, 2009, 15(9): 1788–1794.
WU Bin, NI Weihong, FAN Shuhai, et al. Particle swarm optimization for open vehicle routing problem in dynamic network[J]. Computer Integrated Manufacturing Systems, 2009, 15(9): 1788–1794. (in Chinese) |
| [7] |
赵燕伟, 彭典军, 张景玲, 等.
有能力约束车辆路径问题的量子进化算法[J]. 系统工程理论与实践, 2009, 29(2): 159–167.
ZHAO Yanwei, PENG Dianjun, ZHANG Jingling, et al. Quantum evolutionary algorithm for capacitated vehicle routing problem[J]. Systems Engineering:Theory & Practice, 2009, 29(2): 159–167. (in Chinese) |
| [8] |
李兵, 郑四发, 曹剑东, 等.
求解客户需求动态变化的车辆路径规划方法[J]. 交通运输工程学报, 2007, 7(1): 106–110.
LI Bing, LI Sifa, CAO Jiandong, et al. Method of solving vehicle routing problem with customers' dynamic request[J]. Journal of Traffic and Transportation Engineering, 2007, 7(1): 106–110. (in Chinese) |
| [9] |
陈火根, 丁红钢, 程耀东.
物流配送中心车辆调度模型与遗传算法设计[J]. 浙江大学学报:工学版, 2003, 37(5): 513–516.
CHEN Huogen, DING Honggang, CHENG Yaodong. Model and its genetic algorithm design of the vehicle routing problem with time windows for distribution center[J]. Journal of Zhejiang University:Engineering Science, 2003, 37(5): 513–516. (in Chinese) |
| [10] |
郎茂祥, 胡思继.
用混合遗传算法求解物流配送路径优化问题的研究[J]. 中国管理科学, 2002, 10(5): 51–56.
LANG Maoxiang, HU Siji. Study on the optimization of physical distribution routing problem by using hybrid genetic algorithm[J]. Chinese Journal of Management Science, 2002, 10(5): 51–56. (in Chinese) |
| [11] | Novoa C, Storer R. An approximate dynamic programming approach for the vehicle routing problem with stochastic demands[J]. European Journal of Operational Research, 2009, 196(2): 509–515. DOI:10.1016/j.ejor.2008.03.023 |
| [12] | Branchini R M, Armentano V A, Lokketangen A. Adaptive granular local search heuristic for a dynamic vehicle routing problem[J]. Computers & Operations Research, 2009, 36(11): 2955–2968. |
| [13] | Müller J. Approximative solutions to the bicriterion vehicle routing problem with time windows[J]. European Journal of Operational Research, 2010, 202(1): 223–231. DOI:10.1016/j.ejor.2009.04.029 |
| [14] | 石洪波, 郎茂祥. JD多车型配送车辆调度问题的模型及其禁忌搜索算法研究[J]. 长沙交通学院学报, 2005, 21(3): 73–77. |
| [15] |
李冰.
多车型确定性动态车辆调配问题[J]. 管理工程学报, 2006, 20(3): 52–56.
LI Bin. The deterministic dynamic vehicle allocation problem with multiple vehicle type[J]. Journal of Industrial Engineering and Engineering Management, 2006, 20(3): 52–56. (in Chinese) |
| [16] |
王万良, 黄海鹏, 赵燕伟, 等.
基于车辆共享的软时间窗动态需求车辆路径问题[J]. 计算机集成制造系统, 2011, 17(5): 1056–1063.
WANG Wanliang, HUANG Haipeng, ZHAO Yanwei, et al. Dynamic customer demand VRP with soft time windows based on vehicle sharing[J]. Computer Integrated Manufacturing Systems, 2011, 17(5): 1056–1063. (in Chinese) |
| [17] |
李建, 张永, 达庆利.
第三方物流多车型硬时间窗路线问题研究[J]. 系统工程学报, 2008, 23(1): 74–80.
LI Jian, ZHANG Yong, DA Qingli. Research on heterogeneous vehicle routing problem with hard time windows for the third party logistics[J]. Journal of Systems Engineering, 2008, 23(1): 74–80. (in Chinese) |
| [18] |
熊浩, 胡列格.
多车型动态车辆调度及其遗传算法[J]. 系统工程, 2009, 27(10): 21–24.
XIONG Hao, HU Liege. Dynamic vehicle routing problem with multiple vehicle type and its genetic algorithm[J]. Systems Engineering, 2009, 27(10): 21–24. DOI:10.3321/j.issn:1000-6788.2009.10.003 (in Chinese) |
| [19] | Brandao J. A tabu search algorithm for the heterogeneous fixed fleet vehicle routing problem[J]. Computers & Operations Research, 2008, 38(1): 140–151. |
| [20] | 李德毅, 杜鹢. 不确定性人工智能[M]. 北京: 国防工业出版社, 2005. |
| [21] | 邢文训, 谢金星. 现代优化计算方法[M]. 2版. 北京: 清华大学出版社, 2005. |
 2013, Vol. 36
2013, Vol. 36

