锂离子电池由于具有工作电压高、体积小、质量轻、能量高、无记忆效应、自放电小、循环寿命长等优点,而成为21世纪发展的理想能源。其广泛使用面对失效带来事故及损失的难题。例如,2006年11月份停止工作的美国宇航局火星环球探测器,初步调查显示,在航天器进入安全模式后,电池的散热器面向太阳造成电池温度升高继而电池失去了储存电量的能力。对锂离子电池的剩余寿命(Remaining useful life,RUL)进行预测可以有效判断其未来工作能力,及时发现问题,避免严重的事故。
近年来国内在电池电荷状态(state of charge,SOC)估算[1-4]、电池故障诊断[5]等方面进行了大量的研究,例如模糊理论和神经网络被广泛用于电池SOC估算[3-4]和电池故障诊断中。虽然这些研究已取得许多成果,但是受到电池负载条件和使用环境的影响,从这些预测结果出发很难推算出电池的RUL,关于锂离子电池RUL预测方面的研究成果较少。Saha等[6-7]较早关注了锂离子电池RUL研究的意义,他们分别使用差分自回归滑动平均模型、扩展卡尔曼滤波模型、相关向量机模型、支持向量机模型和粒子滤波模型进行电池RUL预测的对比分析。这些研究对多种预测方法进行了对比,但未对基于粒子滤波的剩余寿命预测进行详细探讨。Xing[8]总结了锂离子电池RUL预测中常用的方法,但是并未针对具体的实例进行分析。目前锂离子电池RUL预测研究成果较少,主要是对一般方法的介绍。文中利用锂离子电池寿命试验数据,分析了电池的退化模型,系统研究了基于粒子滤波的锂离子电池RUL预测方法。
寿命预测一般有2类方法:参数模型法和非参数模型法。参数模型包括物理模型和回归数据模型,首先需要建立系统的物理模型,然后通过分析输入、输出以及状态参数间的关系建立系统的回归数据模型。比较物理模型预测结果与实际观测值的差距,将差值带入回归数据模型进行统计分析,用得到的分析值来修正物理模型参数,最终预测RUL。常用的回归数据模型有多项式曲线拟合、卡尔曼滤波、粒子滤波等。文献[9]建立了一个在热循环系统中实时预测PCB板剩余寿命的预测模型。Bhngu等[10]利用状态空间预测法中的扩展卡尔曼滤波算法来预测汽车电池的充放电状态和健康状态。Edwards和Orchard[11]尝试将反馈矫正环与粒子滤波方法相结合,以表达和管理粒子滤波方法的不确定性,延长非线性非高斯系统的RUL。非参数模型法不需要建立系统的数学模型,当系统未知或较难建模时,选择非参数模型法较优。常用的非参数模型有神经网络模型、粗糙集理论、小波神经网络等。
由于锂离子电池工作原理复杂,其内部状态参数很难测量,一般通过采集电池充放电过程中的电流、电压等数据,建立循环次数与容量间的数学模型来预测其剩余寿命。就此美国马里兰大学CALCE中心已经进行了相关试验,并就锂离子电池的剩余寿命预测方法开展了研究工作。国内对电池剩余寿命预测的研究较少,对粒子滤波的研究也主要集中在机动目标跟踪[12]、金融数据分析、计算机视觉[13]等方面。在这些方面粒子滤波都取得了比较好的预测结果,所以文中采用粒子滤波算法(particle filtering,PF)开展锂离子电池的剩余寿命预测研究。
1 锂离子电池容量退化现象随着充放电次数的增加,锂离子电池的容量会发生衰减,如图 1所示,即电池经历了退化过程。造成容量衰减的原因主要有[14-15]:锂离子电池过充电和不可逆的自放电,负极金属锂的沉积,电解液在正极氧化、在负极还原导致的结构变化,电极电化学反应活性的下降,电极材料的电化学、化学溶解和相位变化,腐蚀引起的电流引线损坏。这些化学反应会消耗锂离子,使可循环锂数量减少,并产生其他沉淀物质,金属锂和其他沉淀物质可能阻塞隔膜的空隙,电池内阻因此而增大,容量逐渐减小。
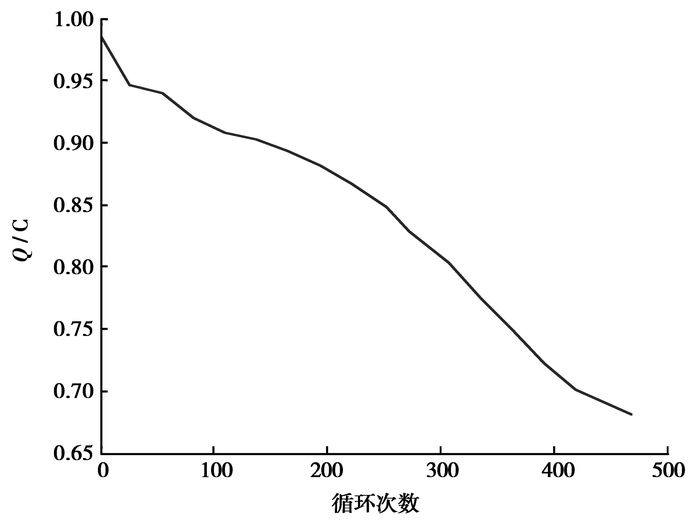
|
图 1 锂离子电池退化现象 |
确定电池的RUL困难重重,主要原因是较难获取电池的性能参数。一般需要对大量电池进行破坏试验来得到性能数据。此外测试时间较长,对于商业电池来说,在其发售前进行长时间的寿命测试是不现实的。高容量电池充放电过程非常长,如果使用加速寿命试验,可能会产生错误的结果。因为电池的寿命与温度、放电速率和放电深度有关,此外加速试验环境可能会引入新的不常见的故障模式。此外,容量数据与循环次数间服从非线性关系,如何通过早期容量数据预测锂离子电池的RUL仍旧是一个难题。
2 粒子滤波的概念及算法早在20世纪50年代,统计学和理论物理学领域就提出了粒子滤波方法,并于60~70年代得到了一定的发展。但是由于退化问题和计算量的制约,并没有引起足够重视。直到90年代Gordon等[16]提出了自举粒子滤波算法,粒子滤波研究才引起人们的关注。而后又有许多改进算法相继被提出,掀起了一股粒子滤波的研究高潮。粒子滤波算法以贝叶斯滤波和蒙特卡洛算法为基础,通过时间更新和量测更新来得到后验概率密度的预测值。
2.1 最优贝叶斯滤波假设动态系统可以由数学模型描述,系统状态方程和测量方程分别为
| $ {x_k} = {f_k}\left( {{x_{k - 1}},{v_{k - 1}}} \right), $ | (1) |
| $ {z_k} = {h_k}\left( {{x_k},{n_k}} \right), $ | (2) |
式中:fk为Rxn×Rxn→Rxn是系统状态xk-1的非线性函数;{vk-1,k∈N}是平稳噪声序列;nx,nv分别是状态和过程噪声的维数;hk为Rxn×Rnn→Rzn是系统状态xk的非线性函数;{nk,k∈N}是平稳噪声序列;nz,nn分别是测量值和测量噪声的维数。
若已知状态的初始概率密度函数p(x0|Z0)=p(x0),那么状态预测方程为
| $ p\left( {{x_k}\left| {{z_{1:k - 1}}} \right.} \right) = \int {p\left( {{x_k}\left| {{x_{k - 1}}} \right.} \right)p\left( {{x_{k - 1}}\left| {{z_{1:k - 1}}} \right.} \right){\rm{d}}{x_{k - 1}}} , $ | (3) |
状态更新方程为
| $ p\left( {{x_k}\left| {{z_{1:k}}} \right.} \right) = \frac{{p\left( {{z_k}\left| {{x_k}} \right.} \right)p\left( {{x_k}\left| {{z_{1:k - 1}}} \right.} \right)}}{{p\left( {{z_k}\left| {{z_{1:k - 1}}} \right.} \right)}}, $ | (4) |
其中
| $ p\left( {{z_k}\left| {{z_{1:k - 1}}} \right.} \right) = \int {p\left( {{z_k}\left| {{x_k}} \right.} \right)p\left( {{x_k}\left| {{z_{1:k - 1}}} \right.} \right){\rm{d}}{x_k}} 。$ | (5) |
利用蒙特卡罗方法可将积分运算变成有限样本点的求和运算。若q(x0:k|z1:k)是一个容易采样的一阶马尔科夫过程,其概率密度分布与p(x0:k|z1:k)相同且已知。假设能从q(x0:k|z1:k)的概率密度分布中抽取N个样本{x0:ki,i=1,2,…,N}(x0:k={x0,…,xk}),那么状态后验概率密度分布可以通过下面的公式近似得到
| $ p\left( {{x_{0:k}}\left| {{z_{1:k}}} \right.} \right) \approx \sum\limits_{i = 1}^N {{{\tilde \omega }_k}\left( {x_{0:k}^i} \right)\delta \left( {{x_{0:k}} - x_{0:k}^i} \right)} , $ | (6) |
式中:ωk(x0:ki)为样本x0:ki(i=1,2,…,N)的权值,δ(·)为狄克拉函数,
| $ \begin{array}{l} {\omega _k} = \frac{{p\left( {{x_{1:k}}\left| {{z_{0:k}}} \right.} \right)p\left( {{x_{0:k}}} \right)}}{{p\left( {{x_{0:k}}\left| {{z_{1:k}}} \right.} \right)}} = \\ \;\;\;\;\;\;\;\;\frac{{p\left( {{x_{1:k}}\left| {{z_{0:k}}} \right.} \right)p\left( {{x_{0:k}}} \right)}}{{q\left( {{x_k}\left| {{x_{0:k - 1}},{x_{1:k}}} \right.} \right)q\left( {{x_{0:k - 1}}\left| {{x_{1:k}}} \right.} \right)}} = \\ \;\;\;\;\;\;\;\;{\omega _{k - 1}}\frac{{p\left( {{z_k}\left| {{x_k}} \right.} \right)p\left( {{x_k}\left| {{x_{k - 1}}} \right.} \right)}}{{q\left( {{x_k}\left| {{x_{0:k - 1}},{x_{1:k}}} \right.} \right)}}。\end{array} $ | (7) |
若q(xk|x0:k-1,z1:k)=q(xk|xk-1,zk),那么ωk仅依赖于xk-1和zk
| $ \omega _k^i \propto \omega _{k - 1}^i\frac{{p\left( {{z_k}\left| {x_k^i} \right.} \right)p\left( {x_k^i\left| {x_{k - 1}^i} \right.} \right)}}{{q\left( {x_k^i\left| {x_{k - 1}^i,{z_k}} \right.} \right)}}, $ | (8) |
标准滤波算法中选取
| $ q\left( {x_k^i\left| {x_{k - 1}^i,{z_k}} \right.} \right) = p\left( {x_k^i\left| {x_{k - 1}^i} \right.} \right), $ | (9) |
那么权值ωki、归一化的权值
| $ \omega _k^i \propto \omega _{k - 1}^ip\left( {{z_k}\left| {x_k^i} \right.} \right), $ | (10) |
| $ \tilde \omega _k^i = \omega _k^i/\sum\limits_{i = 1}^N {\omega _k^i} , $ | (11) |
| $ p\left( {{x_k}\left| {{z_{1:k}}} \right.} \right) \approx \sum\limits_{i = 1}^N {\tilde \omega _k^i\delta \left( {{x_k} - x_k^i} \right)} 。$ | (12) |
制约粒子滤波发展的问题之一就是粒子匮乏现象。随着仿真模拟时间的增加,重要性权值可能集中到少数粒子上,使预测结果偏离实际值。重采样通过舍弃权值小的样本点,复制权值大的样本点以适应系统动态过程。定义有效粒子数
| $ {N_{{\rm{eff}}}} \approx \frac{1}{{\sum\limits_{i = 1}^N {{{\left( {\tilde \omega _k^i} \right)}^2}} }}。$ | (13) |
如果Neff<Nth,则采用重采样算法。Neff越小意味着退化现象越严重,Nth为阈值,一般取2N/3。
为了提高粒子滤波算法的准确性并节约计算时间,Carpenter等提出了分层重采样算法[17]。算法如下:首先将(0,1]分成N个连续互不重合的区间,即
| $ \begin{array}{l} \left( {0,1} \right] = \left( {0,1/N} \right] \cup \cdots \cup \left( {\left\{ {N - 1} \right\}/N,1} \right], \end{array} $ | (14) |
然后对每个子区间采样得Ul=U([{l-1}/N,l/N]) l=1,2,…,N,其中,U([a,b])表示区间[a,b]上的均匀分布。令μl=Ul,得到N个随机数μl,搜索寻找满足条件
| $ \left( {0,1} \right] = \left( {0,1/N} \right] \cup \cdots \cup \left( {\left\{ {N - 1} \right\}/N,1} \right],\sum\limits_{j = 0}^{m - 1} {{{\tilde \omega }_j}} < {\mu _l} \le \sum\limits_{j = 0}^m {{{\tilde \omega }_j}} ,\left( {m = 1,2, \cdots N} \right) $ | (15) |
的整数m,记录xkm。将区间(0,1]按
| $ {\lambda _i} = \sum\limits_{j = 0}^m {{{\tilde \omega }_j}} ,\left( {n = 1, \cdots ,N} \right) $ | (16) |
分成N个小区间,当随机数μl落在第m个区间Im=(λm-1,λ]时,对样本xkm进行复制。新的样本权值为ωki=1/N。研究采用分层重采样算法进行计算。
3 粒子滤波在锂离子电池剩余寿命预测中的应用 3.1 电池退化模型电池容量
| $ \hat Q = \int {I{\rm{d}}t} 。$ | (17) |
锂离子电池的使用过程中,电池的容量会越来越小,一旦下降到预设的临界值,电池就不能作为一个可靠的能源了,也就是电池失效了需要更换。在这里广泛认可的临界值是电池额定容量(
在应用粒子滤波算法之前,首先要建立电池的退化模型。一般可以根据已知的系统物理知识来建立模型,也可以根据经验来建立模型。建立模型最重要的一点是模型必须是健壮的,能够适应系统响应的不同的变化。假设电池的额定容量Qrated=1,定义Q=Qrated·
| $ Q = a \cdot \exp \left( {b \cdot k} \right) + c \cdot \exp \left( {d \cdot k} \right), $ | (18) |
式中:a,b,c,d是模型参数;k是模型的变量,代表充放电循环次数。
研究采用由马里兰大学CALCE中心提供的锂离子电池寿命数据进行模型验证。A1、A2、A3和A4是同一个厂家生产的4个相同型号锂离子电池。通过电子分散光谱可知电池的正极材料为锂钴氧化物,负极材料为石墨碳。在室温下运用Arbin BT2000电池测试系统进行充放电试验,当充电或放电电压达到制造商指定的截止电压时认为一次充电或放电过程完成。电池额定容量为0.9 Ah,放电电流为0.45 Ah。从图 2可以看出,退化模型的曲线能很好地拟合真实的退化数据。
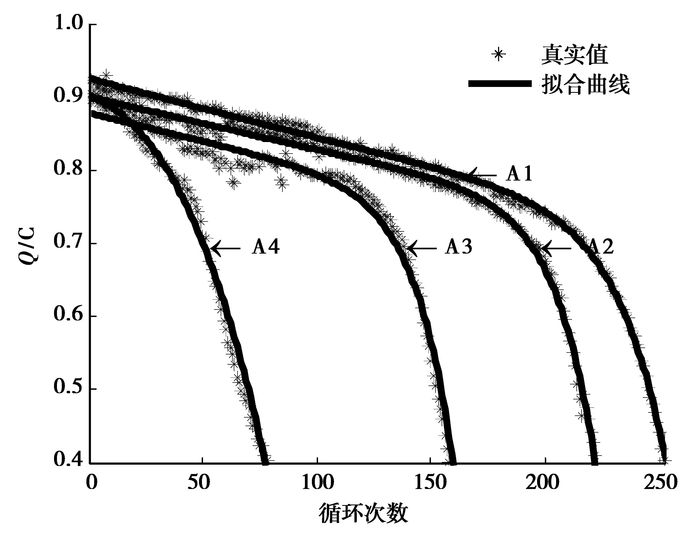
|
图 2 4个电池的退化数据及拟合曲线 |
研究使用电池A1,A2,A3的数据作为训练数据来得出退化模型的初始值,电池A4的数据作为验证数据。
3.2 锂离子电池剩余寿命预测的概率密度函数计算粒子滤波算法用N个采样值近似后验概率密度函数,每个采样值对应一组模型参数[a,b,c,d],Q可以表示成采样值乘以对应权重的求和运算为
| $ {Q_k} \approx \sum\limits_{i = 1}^N {\omega _k^i\delta \left( {{x_k} - x_k^i} \right)} , $ | (19) |
式中:xki=[aki,bki,cki,dki],i=1…N;ωki为对应权值;δ(·)为狄克拉函数。
当循环次数为k时,对应xki(i=1…N)的p步预测为
| $ Q_{k + p}^i = a_k^i\exp \left[ {b_k^i \cdot \left( {k + p} \right)} \right] + c_k^i\exp \left[ {d_k^i \cdot \left( {k + p} \right)} \right]。$ | (20) |
文中选取0.7Qrated作为电池失效的临界值,通过计算下式即可得到电池失效时的充放电循环次数
| $ 0.7{Q_{{\rm{rated}}}} = a_k^i\exp \left( {b_k^i \cdot L_k^i} \right) + c_k^i\exp \left( {d_k^i \cdot L_k^i} \right)。$ | (21) |
已知电池的初始容量Q0(Q0=Qrated)和前面k个测量数据(Q1,…,Qk),进行PF剩余寿命预测分析,其概率密度函数为
| $ P\left( {{L_{k + p}}\left| {{Q_{0:k}}} \right.} \right) \approx \sum\limits_{i = 1}^N {\omega _k^i\delta \left( {{L_{k + p}} - L_{k + p}^i} \right)} 。$ | (22) |
首先借助Matlab曲线拟合工具箱对3组实验数据A1,A2,A3进行拟合,得到经验公式(18)的参数a,b,c,d(见表 1);为了减少特定电池参数对电池A4的影响,这里取a,b,c,d的平均值a,b,c,d作为电池A4退化模型的初始值。
| 表 1 A1、A2、A3模型参数 |
初始值:
| $ \bar a = - 0.0000083499, $ |
| $ \bar b = 0.055237, $ |
| $ \bar c = 0.90097, $ |
| $ \bar d = - 0.00088543。$ |
为了更好地模拟影响真实电池寿命的各种随机因素,假设参数a,b,c,d和容量Q含有高斯噪声。将初始值代入经验公式(18)即可得到初始退化模型。利用电池A4的已知数据来更新初始退化模型就能得到电池A4的剩余寿命预测曲线。
结合粒子滤波算法与锂离子经验退化模型可知,锂离子电池系统状态转移方程为
| $ {x_k} = \left( {{a_k};{b_k};{c_k};{d_k}} \right), $ | (23) |
| $ \left. \begin{array}{l} {a_k} = {a_{k - 1}} + {\omega _a}\;\;\;{\omega _a} \sim N\left( {0,{\sigma _a}} \right)\\ {b_k} = {b_{k - 1}} + {\omega _b}\;\;\;{\omega _b} \sim N\left( {0,{\sigma _b}} \right)\\ {c_k} = {c_{k - 1}} + {\omega _c}\;\;\;{\omega _c} \sim N\left( {0,{\sigma _c}} \right)\\ {d_k} = {d_{k - 1}} + {\omega _d}\;\;\;{\omega _d} \sim N\left( {0,{\sigma _d}} \right) \end{array} \right\}。$ | (24) |
量测方程为
| $ \begin{array}{*{20}{c}} {{Q_k} = {a_k}\exp \left( {{b_k} \cdot k} \right) + {c_k}\exp \left( {{d_k} \cdot k} \right) + v}\\ {v \sim N\left( {0,{\sigma _v}} \right)。} \end{array} $ | (25) |
根据表 1可知,电池A4退化模型初始状态为a0=-0.000 008 349 9,b0=0.055 237,c0=0.900 97,d0=-0.000 885 4;过程噪声为ωa~N(0,1e-10),ωb~N(0,1e-6),ωc~N(0,1e-5),ωd~N(0,1e-7);量测噪声为v~N(0,1e-3);取采样离子数N=1 000。将这些数据带入粒子滤波程序即能更新锂离子电池的状态变量,最终预测出RUL。图 3为已知电池A4前面18个测量数据的PF预测曲线,图 4为已知电池A4前面32个测量数据的PF预测曲线。
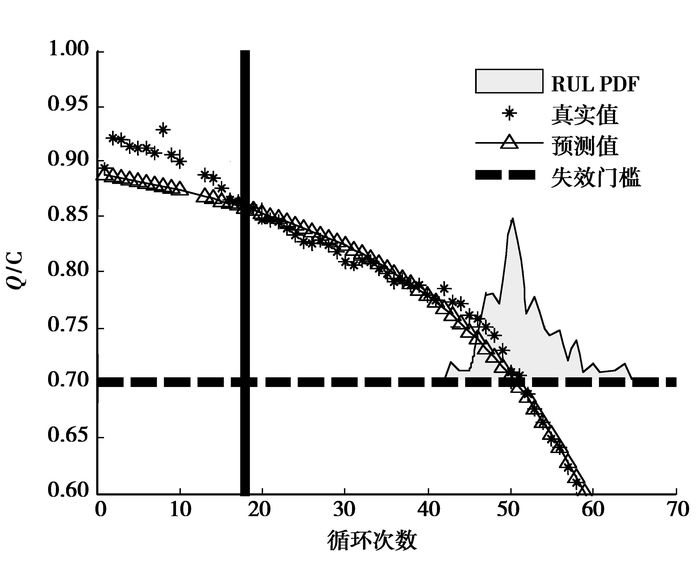
|
图 3 PF预测:已知18个数据 |
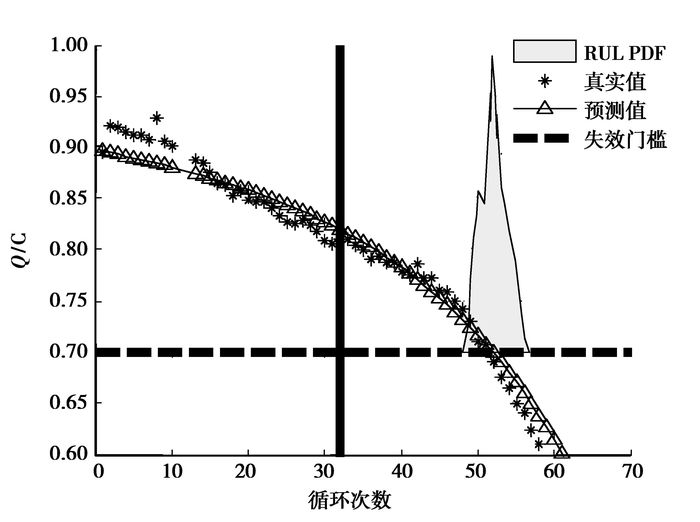
|
图 4 PF预测:已知32个数据 |
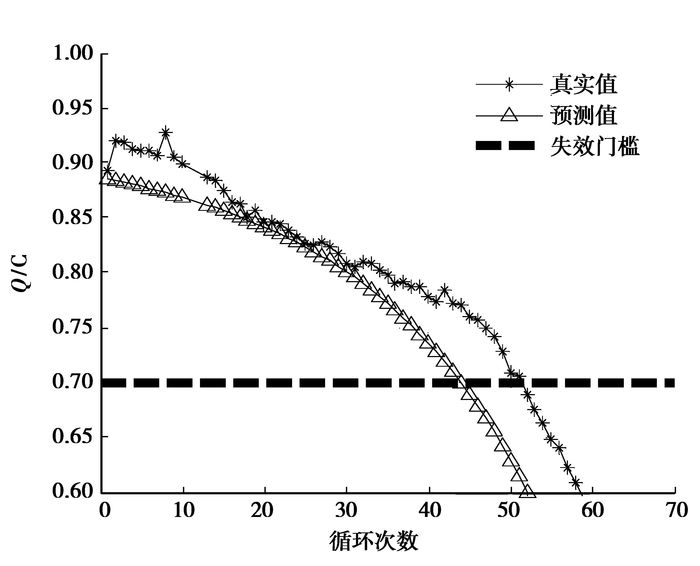
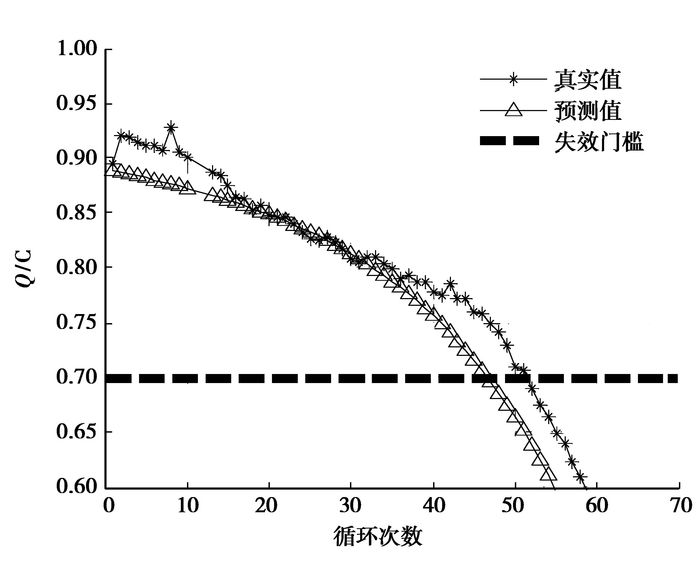
从图 3可以看出最终预测误差为1个循环,黄色区域表示RUL的概率密度函数(Probability distribution function,PDF),这里的概率密度函数分布在[0, 1]的区间上,为了便于比较,将概率密度函数图形向上平移了0.7与寿命预测图形结合在一起,下面的图形采取同样的处理。由于已知的用来更新模型的数据点较少,剩余寿命分布较宽,结果不精确。图 4的最终预测误差也为1个循环,但是随着已知的用来更新模型的数据点增多,剩余寿命分布变得比较集中,预测的结果更准确了,详细比较结果见表 2。
| 表 2 PF、EKF预测结果对比 |
扩展卡尔曼滤波算法是进行预测的一种常用算法。为了进一步说明粒子滤波的优越性,针对相同的电池数据,应用扩展卡尔曼滤波(Extended kalman filter,EKF)进行对比试验。图 5为已知电池A4前面18个测量数据的EKF预测曲线,图 6为已知电池A4前面32个测量数据的EKF预测曲线。由表 2可看出EKF预测偏离真实值较大,预测结果较差。
|
图 5 EKF预测:已知18个数据 |
|
图 6 EKF预测:已知32个数据 |
有效的寿命预测与健康管理能够预测系统发生故障的概率,及时替换元件从而降低系统的失效率节约成本。利用粒子滤波算法有效地预测了锂离子电池的剩余寿命,其预测误差小于5%。对比实验表明,此预测方法比扩展卡尔曼滤波效果好。相似的,粒子滤波算法同样适用于其他系统的寿命预测。
粒子滤波在很多领域都得出了比较好的预测结果,文中将其引入到锂离子电池剩余寿命预测分析中,结果表明是可行的。重要性函数的选择,以及重采样方法的选择对粒子滤波算法的精度影响较大,未来还需要在这些方面做进一步的探索。
致谢 文中数据来源于美国马里兰大学CALCE中心,感谢CALCE中心提供的帮助。
| [1] | 张金灵. 电动汽车智能电池系统的研究[D]. 北京: 北京交通大学硕士学位论文, 2010. http://cdmd.cnki.com.cn/article/cdmd-10004-2010120000.htm |
| [2] |
胡益民, 冯冠平, 刘岩.
基于阻抗谱技术的蓄电池荷电状态的估测[J]. 电工技术学报, 2009, 24(5): 225–228.
HU Yimin, FENG Guanping, LIU Yan. Estimating state-of-charge of storage battery based on impedance spectra technology[J]. Transactions of China Electrotechnical Society, 2009, 24(5): 225–228. (in Chinese) |
| [3] |
李革臣, 江海, 王海英.
基于模糊神经网络的电池剩余电量计算模型[J]. 测试技术学报, 2007, 21(5): 405–409.
LI Gechen, JIANG Hai, WANG Haiying. The SOC compute model of batteries based on fuzzy neural network[J]. Journal of Test and Measurement Technology, 2007, 21(5): 405–409. (in Chinese) |
| [4] |
彭志远, 杨亚联, 秦大同, 等.
一种估计混合动力用Ni-MH电池单体SOC的方法[J]. 重庆大学学报, 2011, 34(5): 19–25.
PENG Zhiyuan, YANG Yalian, QIN Datong, et al. A method for calculating SOC of single Ni-MH battery used in hybrid electric vehicles[J]. Journal of Chongqing University, 2011, 34(5): 19–25. DOI:10.11835/j.issn.1000-582X.2011.05.004 (in Chinese) |
| [5] |
熊茜, 陈启宏, 全睿.
基于神经网络专家系统的燃料电池发动机故障诊断系统设计[J]. 仪表技术, 2010(4): 31–34, 38.
XIONG Qian, CHEN Qihong, QUAN Rui. Design of fault diagnosis system for fuel cell engine based on neural networks expert system[J]. Instrumentation Technology, 2010(4): 31–34, 38. (in Chinese) |
| [6] | Saha B, Goebel K, Christophersen J. Comarison of prognostic algorithms for estimating remaining useful life of batteries[J]. Transactions of the Institute of Measurement and Control, 2009, 31(3/4): 293–308. |
| [7] | Saha B, Goebel K, Poll S, et al. Prognostics methods for battery health monitoring using a Bayesian framework[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(2): 291–296. DOI:10.1109/TIM.2008.2005965 |
| [8] | Xing Y J, Williard N, Tsui K L, et al. A comparative review of prognostics-based reliability methods for lithium batteries[C]//Proceedings of the 2011 Prognostics & System Health Management Conference, May 24-25, 2011, Shenzhen, China. Piscataway:IEEE Press, 2011:1-6. |
| [9] | Rouet V, Minault F, Diancourt G, et al. Concept of smart integrated life consumption monitoring system for electronics[J]. Microelectronics Reliability, 2007, 47(12): 1921–1927. DOI:10.1016/j.microrel.2007.02.019 |
| [10] | Bhangu B, Bentley P, Stone D A, et al. Nonlinear observers for predicting state-of-charge and state-of-health of lead-acid batteries for hybrid-electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2005, 54(3): 783–794. DOI:10.1109/TVT.2004.842461 |
| [11] | Edwards D, Orchard M E, Tang L, et al. Impact of input uncertainty on failure prognostics algorithms:extending the remaining useful life of nonlinear system[C/OL]//Annual Conference of the Prognostics and Health Management Society, Portland, Oregaon, USA, October 10-14, 2010.[2011-06-30]. http://icsl.gatech.edu/aa/images/1/1d/Derek_PHM_2010.pdf. |
| [12] |
胡振涛, 潘泉, 杨峰, 等.
基于多模型粒子滤波的机动多目标跟踪算法[J]. 四川大学学报:工程科学版, 2010, 42(4): 136–141.
HU Zhentao, PAN Quan, YANG Feng, et al. Maneuvering multiple target tracking algorithm based on multiple model particle filter[J]. Journal of Sichuan University:Engineering Science Edition, 2010, 42(4): 136–141. (in Chinese) |
| [13] | 胡士强, 敬忠良. 粒子滤波原理及其应用[M]. 北京: 科学出版社, 2010. |
| [14] |
唐志远, 阮艳莉.
锂离子电池容量衰减机理的研究进展[J]. 化学进展, 2005, 17(1): 1–7.
TANG Zhiyuan, RUAN Yanli. Progress in capacity fade mechanism of Lithium ion battery[J]. Progress in Chemistry, 2005, 17(1): 1–7. (in Chinese) |
| [15] |
李伟善, 邱仕洲.
锂离子电池容量衰减的原因分析[J]. 电池工业, 2001, 6(1): 21–24.
LI Weishan, QIU Shizhou. Causes for capacity decrease in Li ion batteries[J]. Chinese Battery Industry, 2001, 6(1): 21–24. (in Chinese) |
| [16] | Gordon N J, Salmond D J, Smith A F M. Novel approach to nonlinear/non-Gaussian bayesian state estimation[J]. IEE Proceedings F Radar and Signal Processing, 1993, 140(2): 107–113. DOI:10.1049/ip-f-2.1993.0015 |
| [17] | Carpenter J, Clifford P, Fearnhead P. Improved particle filter for nonlinear problems[J]. IEE Proceedings:Radar, Sonar and Navigation, 1999, 146(1): 2–7. DOI:10.1049/ip-rsn:19990255 |
| [18] | Saha B, Goebel K. Uncertainty management for diagnostics and prognostics of batteries using Bayesian techniques[C]//Proceedings of the 2008 IEEE Aerospace Conference, March 1-8, 2008, Big Sky, MT. Piscataway:IEEE Press, 2008:1-8. |
 2013, Vol. 36
2013, Vol. 36

