大规模风电场并入电网,使得风电在电力系统中的比重逐步提高。为此,各国陆续制定了风电并网相关技术规范,以确保风电并网后的电能质量和系统安全[1]。其中,故障穿越或低电压穿越(LVRT)能力是对风电机组提出的最为挑战的要求。采用全功率变换器并网的直驱式永磁同步风力发电机具有更高的效率以及更低的维护成本,是未来海上风电装机的主力机型。鉴于其突出的优势,对直驱式永磁同步风电系统的低电压穿越能力的研究日渐受到关注[2-5]。
电网发生不对称故障(单相对地短路、两相对地短路等)的情况占电网故障的绝大多数[6],因此研究非对称故障情况下的直驱永磁同步风力发电机的控制策略具有很强的现实意义和应用价值。低电压穿越首先要求在电网电压跌落至规定电压极限之上时,风电机组依然能够稳定安全运行,即要求机组不过流、不过压;同时还要向电网提供与故障时电网电压成比例的有功功率[7-9],新的风电并网技术规范更要求风电机组能够提供一定的无功功率支持[3]。同时,对于高功率应用的兆瓦级风电全功率变换器而言,由于电力电子器件本身损耗的限制,其开关频率较低。相对而言,并网电抗器上存在不容忽略的功率分量,因此需要考虑并网电抗器对不对称故障下控制策略的影响。另外,还需要研究不同故障情况下控制策略的适用性。
目前,已有一些文献针对电网不对称故障下该型风电机组的控制进行了研究。文献[8]以控制电网负序电流至零为目标,结合变桨控制,实现了一定意义上的低电压穿越,然而机组输出有功功率、直流侧电压依然存在2倍频波动。基于正序旋转坐标下的电压波动量反馈控制方法[6],可实现有功功率2倍频波动分量的抑制,不过其控制算法存在固有缺陷:电流给定含有2倍频波动,PI调节器无法实现无差跟踪。采用正、负序旋转坐标下双电流环控制[9]独立调节正、负序电流,在电网单相对地短路故障情况下取得了较为满意的控制效果,但整个控制策略并未考虑电网侧变换器过流的问题。
针对2 MW直驱式永磁同步风力发电机控制系统,详细分析了电网不对称故障下电网侧变换器交、直流两侧功率特性。协调控制电机侧变换器,在正、负序旋转坐标下,利用直流侧电压弱控制思想[10]设计了以抑制网侧有功功率2倍频波动为目的的双矢量电流控制策略。结果表明,改进的控制策略在不同的电网不对称故障情况下均具有良好的控制性能。
1 电网侧变换器控制及问题分析 1.1 不对称故障下电网侧变换器控制策略基于全功率变换器的直驱式永磁同步风力发电机系统实现了电网与发电机之间的解耦,在电网出现故障时,选择合理的电网侧变换器控制策略,可以使得电机侧的控制较少甚至不受电网故障的影响。因此,为实现直驱式风电机组的低电压穿越,网侧变换器在电网故障时的控制策略至关重要。
带全功率并网变换器的直驱式永磁同步风力发电机系统如图 1所示。图中,Rg、Lg分别为电网侧变换器的并网电抗器电阻及电感;C为直流电容。

|
图 1 带全功率并网变换器的直驱式永磁同步风力发电机系统 |
不对称电网故障时,永磁同步风力发电机系统馈入电网的功率为[11]
| $ \begin{array}{l} {S_g} = {U_g}I_g^ * = \\ 3/2 \cdot \left( {u_{{\rm{gdq}}}^p{e^{j\omega t}} + u_{{\rm{gdq}}}^n{e^{ - j\omega t}}} \right) \cdot \\ \left( {i{{_{{\rm{gdq}}}^p}^ * }{e^{ - j\omega t}} + i{{_{{\rm{gdq}}}^n}^ * }{e^{j\omega t}}} \right)。\end{array} $ | (1) |
相应的有功、无功功率为
| $ \begin{array}{l} {S_{\rm{g}}} = {p_{\rm{g}}}\left( t \right) + j{q_{\rm{g}}}\left( t \right) = \\ \;\;\;\;\;\;\;\left( {{P_{g0}} + {P_{gc2}}\cos \left( {2\omega t} \right) + {P_{gs2}}\sin \left( {2\omega t} \right)} \right) + \\ \;\;\;\;\;\;\;\;j\left( {{Q_{g0}} + {Q_{gc2}}\cos \left( {2\omega t} \right) + } \right.\\ \;\;\;\;\;\;\;\;\left. {{Q_{gs2}}\sin \left( {2\omega t} \right)} \right), \end{array} $ | (2) |
式中:Ug、Ig为网侧电压、电流;ugdqp、ugdqn、igdqp、igdqn为正、负序电网电压、电流;Pg0、Qg0为馈入电网的有功、无功功率的直流分量;Pgc2、Pgs2、Qgc2、Qgs2为有功、无功功率的正、余弦2倍电网频率波动分量。
综合以上2式得到
| $ \left[ \begin{array}{l} {P_{g0}}\\ {P_{gc2}}\\ {P_{gs2}}\\ {Q_{g0}}\\ {Q_{gc2}}\\ {Q_{gs2}} \end{array} \right] = \frac{3}{2} \cdot \left[ {\begin{array}{*{20}{c}} {u_{{\rm{gd}}}^p}&{u_{{\rm{gq}}}^p}&{u_{{\rm{gd}}}^n}&{u_{{\rm{gq}}}^n}\\ {u_{{\rm{gd}}}^n}&{u_{{\rm{gq}}}^n}&{u_{{\rm{gd}}}^p}&{u_{{\rm{gq}}}^p}\\ {u_{{\rm{gq}}}^n}&{ - u_{{\rm{gd}}}^n}&{ - u_{{\rm{gq}}}^p}&{u_{{\rm{gd}}}^p}\\ {u_{{\rm{gq}}}^p}&{ - u_{{\rm{gd}}}^p}&{u_{{\rm{gq}}}^n}&{ - u_{{\rm{gd}}}^n}\\ {u_{{\rm{gq}}}^n}&{ - u_{{\rm{gd}}}^n}&{u_{{\rm{gq}}}^p}&{ - u_{{\rm{gd}}}^p}\\ { - u_{{\rm{gd}}}^n}&{ - u_{{\rm{gq}}}^n}&{u_{{\rm{gd}}}^p}&{u_{{\rm{gq}}}^p} \end{array}} \right] \cdot \left[ \begin{array}{l} i_{{\rm{gd}}}^p\\ i_{{\rm{gq}}}^p\\ i_{{\rm{gd}}}^n\\ i_{{\rm{gq}}}^n \end{array} \right]。$ | (3) |
为消除有功功率的2倍频波动,需令式(3)中Pc2和Ps2为零,即
| $ \left\{ \begin{array}{l} {P_{g0}} = P_{g0}^ * ;\\ {P_{gc2}} = 0;\\ {P_{gs2}} = 0;\\ {Q_{g0}} = Q_{g0}^ * 。\end{array} \right. $ | (4) |
则电流参考命令值为
| $ \left\{ \begin{array}{l} i{{_{{\rm{gd}}}^p}^*} = 2/3 \cdot u_{{\rm{gd}}}^p\left( {{k_u}P_{g0}^ * } \right){D_d};\\ i{{_{{\rm{gq}}}^p}^*} = 2/3 \cdot u_{{\rm{gd}}}^pQ_{g0}^ * {D_q};\\ i{{_{{\rm{gd}}}^n}^*} = - {k_d}i{{_{{\rm{gd}}}^p}^*} - {k_q}i{{_{{\rm{gq}}}^p}^*};\\ i{{_{{\rm{gq}}}^n}^*} = - {k_q}i{{_{{\rm{gd}}}^p}^*} + {k_d}i{{_{{\rm{gq}}}^p}^*}。\end{array} \right. $ | (5) |
式中
| $ {D_d} = 1/\left( {u{{_{{\rm{gd}}}^p}^2} + u{{_{{\rm{gq}}}^p}^2} - u{{_{{\rm{gd}}}^n}^2} - u{{_{{\rm{gq}}}^n}^2}} \right);{k_d} = u_{{\rm{gd}}}^n/u_{{\rm{gd}}}^p; $ |
| $ {D_q} = 1/\left( {u{{_{{\rm{gd}}}^p}^2} + u{{_{{\rm{gq}}}^p}^2} - u{{_{{\rm{gd}}}^n}^2} - u{{_{{\rm{gq}}}^n}^2}} \right);{k_q} = u_{{\rm{gq}}}^n/u_{{\rm{gd}}}^p。$ |
在忽略并网电抗器上吸收的功率及电网侧变换器自身功率损耗的情况下,按照上述算法在正、负序双电流环控制策略下,如果控制得当,在消除馈入电网的有功功率波动的同时,亦可使得直流侧电压无2倍频波动[12]。
1.2 考虑并网电抗器的功率特性分析实际上,兆瓦级全功率并网变换器由于损耗的限制,开关频率较低,约1~2 kHz,其并网电抗器的电感值相对较大,相应其上的功率波动不能忽略。因此,在研究不对称电网故障下的电网侧变换器交、直流两端功率关系时,需要考虑并网电抗器上的功率波动[13]。
并网电抗器电感、电阻吸收的功率分别为
| $ \begin{array}{l} {S_L} = {U_L}I_g^ * = {L_g}\frac{{{\rm{d}}{I_{\rm{g}}}}}{{{\rm{d}}t}}I_g^ * = \\ \;\;\;\;\;\;\;3/2 \cdot L\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {i_{{\rm{gdq}}}^p{e^{j\omega t}} + i_{{\rm{gdq}}}^n{e^{ - j\omega t}}} \right) \cdot \\ \;\;\;\;\;\;\;\left( {i{{_{{\rm{gdq}}}^p}^ * }{e^{ - j\omega t}} + i{{_{{\rm{gdq}}}^n}^ * }{e^{j\omega t}}} \right); \end{array} $ | (6) |
| $ \begin{array}{l} {S_R} = {U_R}I_g^ * = R{I_g}I_g^ * = \\ \;\;\;\;\;\;\;3/2 \cdot R\left( {i_{{\rm{gdq}}}^p{e^{j\omega t}} + i_{{\rm{gdq}}}^n{e^{ - j\omega t}}} \right) \cdot \\ \;\;\;\;\;\;\;\left( {i{{_{{\rm{gdq}}}^p}^ * }{e^{ - j\omega t}} + i{{_{{\rm{gdq}}}^n}^ * }{e^{j\omega t}}} \right)。\end{array} $ | (7) |
整理以上2式,并网电抗器吸收的有功功率为
| $ \Delta {P_0} = 3/2 \cdot {R_g}\left( {i{{_{{\rm{gd}}}^p}^2} + i{{_{{\rm{gq}}}^p}^2} + i{{_{{\rm{gd}}}^n}^2} + i{{_{{\rm{gq}}}^n}^2}} \right); $ | (8) |
| $ \begin{array}{l} \Delta {P_{c2}} = 3 \cdot \left[ {{R_g}\left( {i_{{\rm{gd}}}^pi_{{\rm{gd}}}^n + i_{{\rm{gq}}}^pi_{{\rm{gq}}}^n} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\omega {L_g}\left( {i_{{\rm{gd}}}^pi_{{\rm{gq}}}^n - i_{{\rm{gq}}}^pi_{{\rm{gd}}}^n} \right)} \right]; \end{array} $ | (9) |
| $ \begin{array}{l} \Delta {P_{s2}} = 3 \cdot \left[ {{R_g}\left( {i_{{\rm{gd}}}^pi_{{\rm{gq}}}^n - i_{{\rm{gq}}}^pi_{{\rm{gd}}}^n} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\omega {L_g}\left( {i_{{\rm{gd}}}^pi_{{\rm{gd}}}^n + i_{{\rm{gq}}}^pi_{{\rm{gq}}}^n} \right)} \right]。\end{array} $ | (10) |
对应的无功功率为
| $ \Delta {Q_0} = 3/2 \cdot \omega {L_g}\left( {i{{_d^p}^2} + i{{_q^p}^2} - i{{_d^n}^2} - i{{_q^n}^2}} \right), $ | (11) |
其中:ΔP0、ΔPc2、ΔPs2分别为并网电抗器吸收的有功功率直流分量、余弦、正弦分量;ΔQ0为无功功率分量。
直流侧电容功率平衡方程为
| $ C\frac{{{\rm{d}}{u_{{\rm{dc}}}}}}{{{\rm{d}}t}}{u_{{\rm{dc}}}} + {P_c} = {P_s}, $ | (12) |
其中,Pc为电网侧变换器端口输出有功功率,Ps为发电机输出有功功率
| $ \begin{array}{l} {P_c} = {P_g} + {P_\Delta } = \\ \;\;\;\;\;\;\;{P_g} + \Delta {P_0} + \Delta {P_{c2}} + \Delta {P_{s2}}。\end{array} $ | (13) |
按照不对称控制策略,消除了馈入电网的有功功率2倍频波动后,其值只剩下直流分量,即Pg=Pg0,因此,
| $ \begin{array}{l} \frac{{{\rm{d}}{u_{{\rm{dc}}}}}}{{{\rm{d}}t}} = \frac{{{P_s} - {P_{g0}} - \left( {\Delta {P_0} + \Delta {P_{c2}} + \Delta {P_{s2}}} \right)}}{{C{u_{{\rm{dc}}}}}} = \\ \;\;\;\;\;\;\;\;\;\;3 \cdot \left\{ {\left( {{u_{{\rm{sd}}}}{i_{{\rm{sd}}}} + {u_{{\rm{sq}}}}{i_{{\rm{sq}}}}} \right) - \left( {u_{{\rm{gd}}}^pi_{{\rm{gd}}}^p + u_{{\rm{gq}}}^pi_{{\rm{gq}}}^p + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {u_{{\rm{gd}}}^ni_{{\rm{gd}}}^n + u_{{\rm{gq}}}^ni_{{\rm{gq}}}^n} \right) - {R_g}\left( {i{{_{{\rm{gd}}}^p}^2} + i{{_{{\rm{gq}}}^p}^2} + i{{_{{\rm{gd}}}^n}^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {i{{_{{\rm{gq}}}^n}^2}} \right) - 2\left[ {{R_g}\left( {i_{{\rm{gd}}}^pi_{{\rm{gd}}}^n + i_{{\rm{gq}}}^pi_{{\rm{gq}}}^n} \right) + \omega {L_g} \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left( {i_{{\rm{gd}}}^pi_{{\rm{gq}}}^n - i_{{\rm{gq}}}^pi_{{\rm{gd}}}^n} \right)} \right]\cos \left( {2\omega t} \right) - 2\left[ {{R_g}\left( {i_{{\rm{gd}}}^pi_{{\rm{gq}}}^n - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left. {i_{{\rm{gq}}}^pi_{{\rm{gd}}}^n} \right) - \omega {L_g}\left( {i_{{\rm{gd}}}^pi_{{\rm{gd}}}^n + i_{{\rm{gq}}}^pi_{{\rm{gq}}}^n} \right)} \right] \cdot \\ \;\;\;\;\;\;\;\;\;\;\left. {\sin \left( {2\omega t} \right)} \right\}/2C{u_{{\rm{dc}}}}。\end{array} $ | (14) |
由式(14)可知,电网侧变换器按照传统的电压外环、双矢量电流内环控制方式,在实现馈入到电网的有功功率无2倍频波动的同时,是无法消除直流侧电压波动的,反之亦是如此。造成上述结果的根本原因在于,并网电抗器在电网不对称故障时吸收的有功功率同样存在不可忽略的2倍频波动。因此,需要对不对称电网故障下的全功率永磁同步风力发电机的控制策略进行改进。
2 改进的故障穿越控制策略 2.1 网侧电流参考命令电网不对称短路故障下,控制目标为直驱式风电系统馈入电网的有功功率无波动。采用上述控制方式时,电网存在负序电流,因此易造成过流。为保护电网侧变换器不对称故障下的稳定安全运行,须对电网侧变换器交流侧进行限流。
考虑到负序电流存在下的电流限制为
| $ \sqrt {i{{_{{\rm{gd}}}^p}^2} + i{{_{{\rm{gq}}}^p}^2}} + \sqrt {i{{_{{\rm{gd}}}^n}^2} + i{{_{{\rm{gq}}}^n}^2}} \le {i_{\max }}。$ | (15) |
很显然,要对4个电流控制量进行限幅,难度很大。注意到式(5),4个电流限制可以通过设置合适的网侧有功功率参考Pg0*来统一实现。故障情况下馈入电网的有功功率目标值随着电网电压的跌落而降低,可以用电网电压跌落因子ku来衡量电网电压跌落程度,ku定义为
| $ {k_u} = \left( {\sqrt {u_{{\rm{gd}}}^{{p^2}} + u_{{\rm{gq}}}^{{p^2}}} - \sqrt {u_{{\rm{gd}}}^{{n^2}} + u_{{\rm{gq}}}^{{n^2}}} } \right)/{u_{{\rm{gd}}}}, $ | (16) |
其中,ugd为电网电压正常时d轴电压。
按照ku成比例的降低有功功率的目标值,即令式(4)中Pg0=kuPg0*,因此得到修正后的网侧电流参考命令值为
| $ \left. {\begin{array}{*{20}{c}} {i{{_{{\rm{gd}}}^p}^ * } = 2/3 \cdot u_{{\rm{gd}}}^p\left( {{k_{\rm{u}}}P_{g0}^ * } \right){D_d}}\\ {i{{_{{\rm{gq}}}^p}^ * } = 2/3 \cdot u_{{\rm{gd}}}^pQ_{g0}^ * {D_q}}\\ {i{{_{{\rm{gd}}}^n}^ * } = - {k_d}i{{_{{\rm{gd}}}^p}^ * } - {k_q}i{{_{{\rm{gq}}}^p}^ * }}\\ {i{{_{{\rm{gq}}}^n}^ * } = - {k_q}i{{_{{\rm{gd}}}^p}^ * } + {k_d}i{{_{{\rm{gq}}}^p}^ * }} \end{array}} \right\}。$ | (17) |
因为电网电压的跌落,同时受变换器最大电流的限制,其故障状态下输出的无功能力有限,
| $ {Q_{g\max }} = {k_u}\sqrt {S_{\max }^2 - P_g^2} , $ | (18) |
式中:Smax为网侧输出视在功率最大值,在全功率直驱式风电机组中,一般取值Smax=1.2 Pmax;Pmax为网侧输出最大有功功率。因此
| $ Q_{g0}^ * \le {Q_{g\max }}。$ | (19) |
按照上述电流参考命令进行控制,注入电网的任何一相电流不会超出最大电流限制,从而保证了电网侧变换器的可靠运行。
2.2 基于功率平衡协调的电机侧控制发电机控制系统电流环的动态调节时间可控制在几十ms内,因此在故障过程中可采用限制发电机转矩电流的方式来限制发电机的电磁功率,在不增加额外硬件(如直流侧Crowbar电路[14-15])的情况下,协调实现直驱式永磁同步风力发电机的不对称故障穿越。故障时,调节电机侧变换器输入到直流侧的有功功率Ps,使其值与电网侧变换器馈入到电网的有功功率kuPg0*一致,即要求Ps降低至故障前的ku倍。这种基于功率平衡协调的控制方式,保证了直流侧电容两侧的功率基本相等,在实现网侧不过流的同时,直流侧电压将被控制在一个安全的容限内。电网故障时风机吸收的功率与限制的发电机输出有功功率之差将转化为系统转子动能。由于兆瓦级风机系统的转动惯量巨大,短时故障期间的转速上升很小,因此桨距角控制不被考虑[1-4]。
考虑电网电压跌落因子ku,综合得到电机侧变换器改进控制方案如图 2所示。
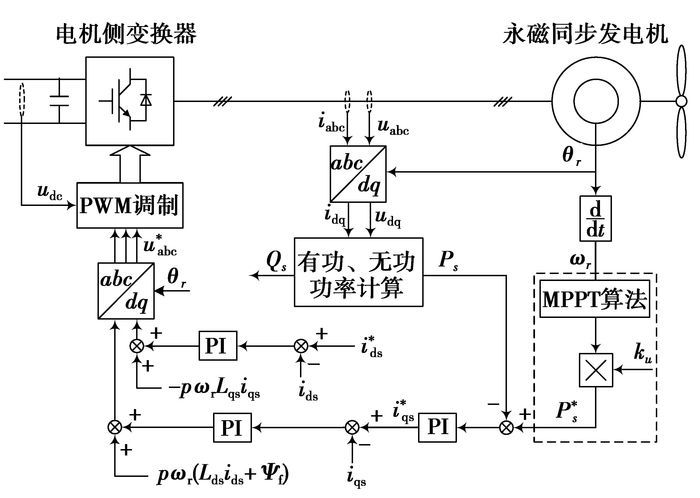
|
图 2 电机侧变换器改进控制方案 |
将式(12)直流侧电容功率平衡方程重写于下
| $ {P_{{\rm{dc}}}} = \frac{1}{2}C\frac{{{\rm{d}}\left( {u_{{\rm{dc}}}^2} \right)}}{{{\rm{d}}t}} = {P_s} - {P_c}, $ | (20) |
将上式变形为
| $ \begin{array}{l} {P_c} = {i_g}{u_{{\rm{dc}}}} = {P_s} - {P_{{\rm{dc}}}} = \\ \;\;\;\;\;\;{u_{{\rm{sd}}}}{i_{{\rm{sd}}}} + {u_{{\rm{sq}}}}{i_{{\rm{sq}}}} - {u_{{\rm{dc}}}}C\frac{{{\rm{d}}{u_{{\rm{dc}}}}}}{{{\rm{d}}t}}, \end{array} $ | (21) |
整理上式,得
| $ {i_g} = \frac{{{u_{{\rm{sd}}}}{i_{{\rm{sd}}}} + {u_{{\rm{sq}}}}{i_{{\rm{sq}}}}}}{{{u_{{\rm{dc}}}}}} - C\frac{{{\rm{d}}{u_{{\rm{dc}}}}}}{{{\rm{d}}t}}, $ | (22) |
上式中,usd、usq、isd、isq分别为发电机d、q轴定子电压、电流。等式右端第1项为电机侧变换器馈入直流侧有功功率的电流量等值反映,将其作为前馈量信息,与直流侧电容电流ic(直流侧电压PI调节器输出)构成直流侧馈入电网侧变换器电流ig,并联合直流侧电压udc一起构成馈入电网的有功功率参考值Pg0*。
不对称故障时应用双矢量电流控制策略,负序电流的注入造成并网电抗器上有功功率也以2倍频的形式波动。这使得直流侧电压无波动和馈入电网有功功率无2倍频波动两者无法兼顾。考虑到故障时间较短,借鉴应用于UPFC的直流侧电容电压弱控制思想[10],利用直流侧电容一定的能量缓冲能力,以直流侧电压波动为代价,把控制系统输出有功功率无2倍频波动作为不对称故障控制的主要目标。据此设计的带前馈的直流侧电压弱控制如图 3所示。电网故障前系统稳态运行时,控制器投入PI1,控制器参数kpn、kin按照稳态无差跟踪控制要求选取;检测到故障后,迅速切换至控制器PI2,控制器参数kpf、kif以电压不失稳控制原则选取。故障时对直流侧电压的控制而言,前馈项(usdisd+usqisq)/udc仅在原理上保证Pc=Ps,电压控制器表现为控制能力的减弱[16]。
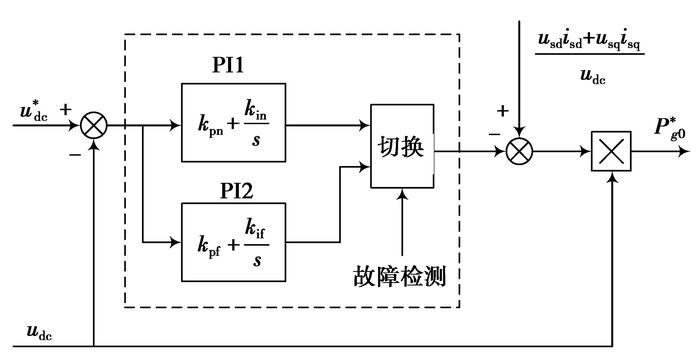
|
图 3 带前馈的直流侧电压弱控制 |
电网侧变换器的改进控制策略如图 4所示。
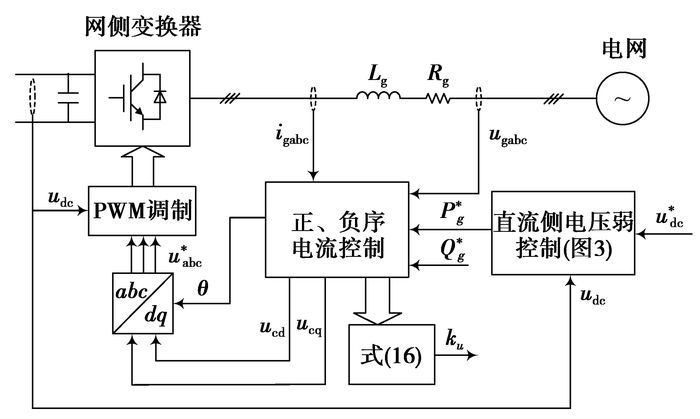
|
图 4 电网侧变换器改进控制方案 |
为验证提出的改进的故障穿越控制策略的有效性,建立1台2 MW直驱永磁同步风力发电机组的系统仿真模型。具体参数如下:永磁同步发电机额定功率2 MW,定子额定电压690 V,定子额定电流1 700 A,定子电阻6 mΩ,交、直轴电感2.6 mH,惯性时间常数为5 s;电网侧变换器并网电抗器电感为0.3 mH,电阻为0.01 Ω,直流侧电容40 mF,直流侧电压设定为1 200 V,变换器开关频率为2 kHz。
分别对单相对地短路、两相对地短路两种故障状况进行仿真验证。故障发生前,机组运行于全功率额定状态:P=2 MW,Q=0 Mvar。1.5 s故障发生,300 ms后故障清除,如图 5所示。
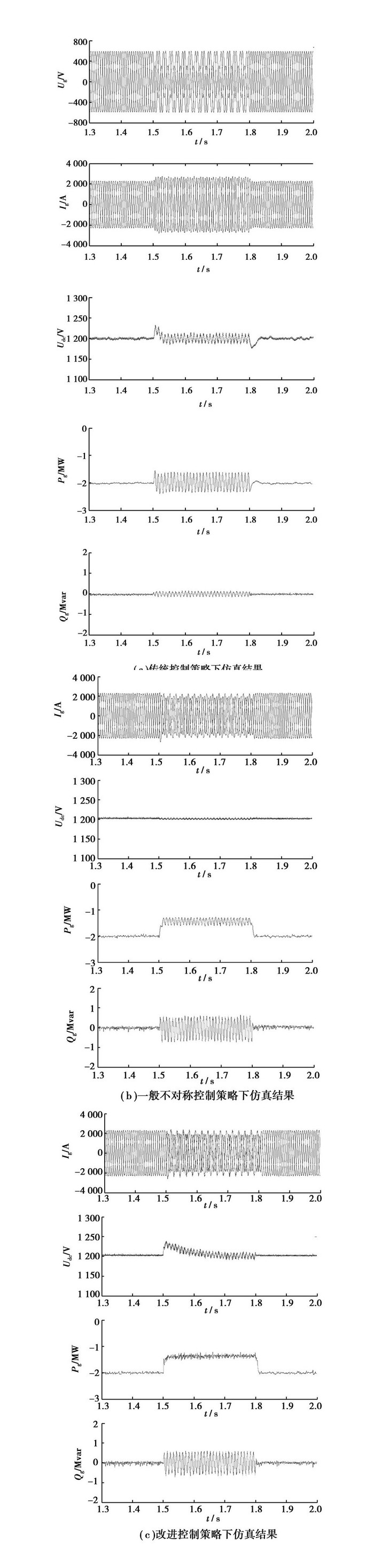
|
图 5 单相对地短路故障时不同控制策略对比仿真结果 |
由图 5(a)可见,1.5~1.8 s期间电网发生单相对地短路故障,单相电压跌落至额定值的50%左右。在传统的正序电网电压定向的矢量控制方式下,网侧有功功率、无功功率及直流侧电压均出现2倍频波动,特别是有功功率波动幅值超过1 MW,这显然对电网故障恢复不利。并且,由于故障时直流侧电压依然被控制在设定值附近,相应的网侧电流升高,超出了额定值17%。若采用一般的不对称故障控制策略,即不考虑并网电抗器对网侧功率的影响,直流侧电压得到了较好的控制,波动很小;但并网电抗器上的功率波动需要网侧功率来平衡,因此其有功功率依然存在一定的2倍频波动(幅值约0.4 MW),见图 5(b)。
如图 5(c)所示,采用提出的改进的不对称故障穿越控制策略,虽然直流侧电压存在一定的2倍频波动,但波动幅度在可承受范围内。改进控制策略的应用基本消除了网侧有功功率的2倍频波动(波动幅值小于0.15 MW)。根据电网电压跌落深度同步降低了发电机的输出有功功率,网侧电流得到了限制,电网电流在1.5~1.8 s的故障期间仍然保持在额定值附近。除了直流侧电压较小的波动外,网侧有功功率2倍频波动消除的代价是无功功率2倍频波动的增大。
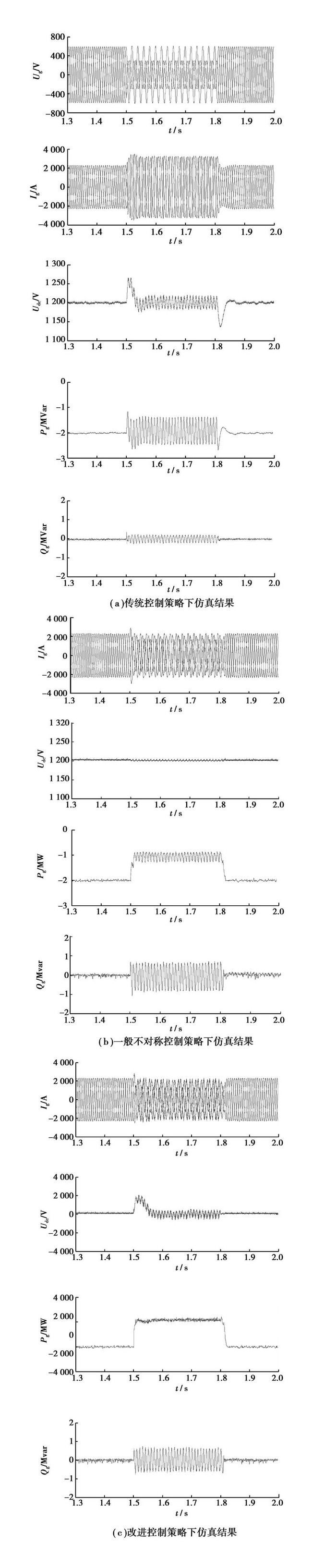
图 6是两相对地短路故障时的对比仿真。分析可知,在两相电压跌落至额定值50%左右的情况下,采用研究的控制策略同样可以使得网侧有功功率的2倍频波动基本消除;基于功率平衡的网侧限流措施使得故障期间网侧电流由1.43倍额定值降低至额定值附近。同时也说明,基于功率平衡协调控制的限流方式在不对称故障程度较深的情况下效果更为显著。以上仿真算例中,改进的控制策略在不同故障情况下的适用性得到了很好的验证。
|
图 6 两相对地短路故障时不同控制策略对比仿真结果 |
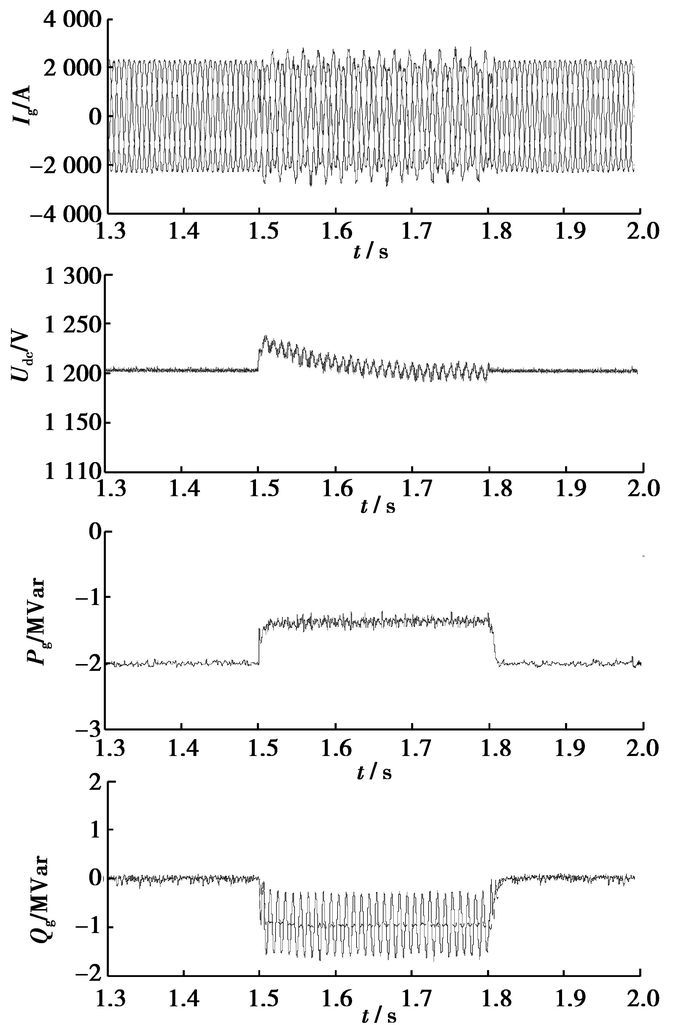
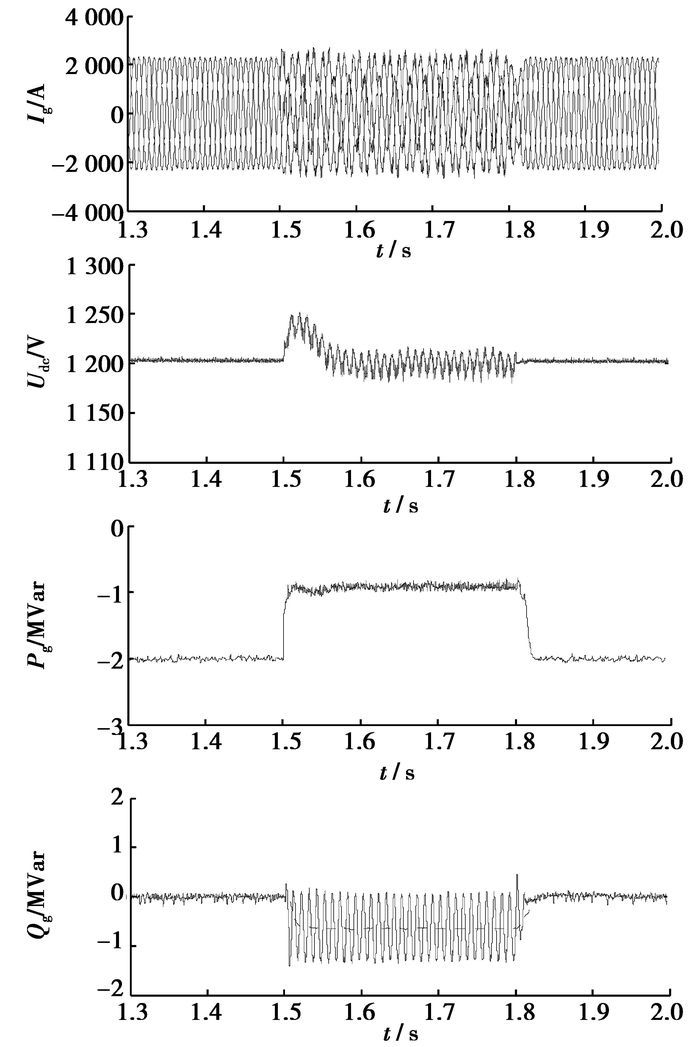
图 7和图 8分别是以上两种不对称短路故障时,直驱式风电机组对电网的无功支持的仿真结果。电网故障期间,机组可以分别提供最多约0.9 MVar以及约0.6 MVar的平均无功功率(图中虚线所示),同时网侧电流均被控制在1.2倍额定电流以下,而直流侧电压和网侧输出有功功率基本不受发出无功功率的影响(对比图 5、图 6中相应的仿真结果)。此仿真结果说明,机组可在实现低电压穿越要求的同时,给予电网一定的无功支持,以利电网电压的恢复。从式(18)以及图 7、图 8的仿真结果可以看出,电网电压跌落程度越深,机组所能提供的无功能力亦越弱。因此,在较为严重的电网故障情况下,电网的无功需求还要联合其他无功补偿设备来满足[3]。
|
图 7 单相对地短路故障时机组对电网的无功支持仿真结果 |
|
图 8 两相对地短路故障时机组对电网的无功支持仿真结果 |
结合直驱式永磁同步风力发电机的运行特性,分析了电网不对称故障情况下并网电抗器对机组输出功率的影响,提出了基于直流侧电压弱控制思想的低电压穿越控制策略。无需额外的硬件电路,改进的控制策略根据不对称故障的电压跌落深度,协调控制发电机输出的有功功率,实现了直流侧电压的基本恒定,同时保证了电网侧变换器输出电流在安全容限内。对1台2 MW直驱式永磁同步风力发电机系统进行仿真验证,结果表明,无论是单相对地短路、两相对地短路故障,提出的改进控制策略均可实现网侧输出有功功率2倍频波动的消除,控制系统具有优良的动、静态性能。
| [1] | Conroy J F, Watson R. Low-voltage ride-through of a full converter wind turbine with permanent magnet generator[J]. IET Renewable Power Generation, 2007, 1(3): 182–189. DOI:10.1049/iet-rpg:20070033 |
| [2] | Wang Z, Nian H, Hu J B.Enhanced control strategies of permanent magnet synchronous wind power generation system under unbalanced grid voltage conditions[C]//Asia-Pacific Power and Energy Engineering Conference, Chengdu, China, 2010:1-4. |
| [3] |
胡书举, 李建林, 许洪华.
永磁直驱风电系统低电压运行特性的分析[J]. 电力系统自动化, 2007, 31(17): 73–77.
HU Shuju, LI Jianlin, XU Honghua. Analysis on the low-voltage-ride-throuth capability of direct-drive permanent magnetic generator wind turbines[J]. Automation of Electric Power Systems, 2007, 31(17): 73–77. DOI:10.3321/j.issn:1000-1026.2007.17.017 (in Chinese) |
| [4] |
姚骏, 廖勇, 庄凯.
电网故障时永磁直驱风电机组的低电压穿越控制策略[J]. 电力系统自动化, 2009, 33(12): 91–95.
YAO Jun, LIAO Yong, ZHUANG Kai. A low voltage ride-through control strategy of permanent magnet direct-driven wind turbine under grid faults[J]. Automation of Electric Power Systems, 2009, 33(12): 91–95. DOI:10.3321/j.issn:1000-1026.2009.12.019 (in Chinese) |
| [5] | Ng C H, Li R, Bumby J. Unbalanced-grid-fault ride-through control for a wind turbine inverter[J]. IEEE Transactions on Industry Applications, 2008, 44(3): 845–856. DOI:10.1109/TIA.2008.921429 |
| [6] |
赵紫龙, 吴维宁, 王伟.
电网不对称故障下直驱风电机组低电压穿越技术[J]. 电力系统自动化, 2009, 33(21): 87–91.
ZHAO Zhilong, WU Weilin, WANG Wei. A low voltage ride through technology for direct-drive wind turbines under unbalanced voltage dips[J]. Automation of Electric Power Systems, 2009, 33(21): 87–91. DOI:10.7500/AEPS200905017 (in Chinese) |
| [7] | Mullane A, Lightbody G, Yacamini R. Wind-turbine fault ride-through enhancement[J]. IEEE Transactions on Power Systems, 2005, 20(4): 1929–1937. DOI:10.1109/TPWRS.2005.857390 |
| [8] |
杨晓萍, 段先锋, 钟彦儒.
直驱永磁同步风电机组不对称故障穿越的研究[J]. 电机与控制学报, 2010, 14(2): 7–12.
YANG Xiaoping, DUAN Xianfeng, ZHONG Yanru. Asymmetrical faults ride-through of directly driven wind turbine with permanent magnet synchronous generator[J]. Electric Machines and Control, 2010, 14(2): 7–12. (in Chinese) |
| [9] |
孙素娟, 赵紫龙, 陈玮.
电网不对称时直驱风电机组双电流环控制策略[J]. 水电自动化与大坝监测, 2010, 34(1): 41–45.
SUN Sujuan, ZHAO Zhilong, CHEN Wei. Dual current-loop control strategy for converter of directly-driven wind generation under grid conditions[J]. Hydropower Automation and Dam Monitoring, 2010, 34(1): 41–45. (in Chinese) |
| [10] |
陈众, 颜伟, 徐国禹, 等.
基于直流侧电容电压弱控制策略的UPFC二阶段控制器设计[J]. 中国电机工程学报, 2004, 24(1): 49–53.
CHEN Zhong, YAN Wei, XU Guoyu, et al. Design of UPFC Soft-complete controller based on the dc link capacitor voltage soft control strategy[J]. Proceedings of the CSEE, 2004, 24(1): 49–53. (in Chinese) |
| [11] | Yongsug S, LIPO T A. Modeling and analysis of instantaneous active and reactive power for PWM AC/DC converter under generalized unbalanced network[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1530–1540. DOI:10.1109/TPWRD.2005.860274 |
| [12] | Hong S S, Kwanghee N. Dual current control scheme for PWM converter under unbalanced input voltage conditions[J]. IEEE Transactions on Industrial Electronics, 1999, 46(5): 953–959. DOI:10.1109/41.793344 |
| [13] | Yazdania A, Iravani R. A unified dynamic model and control for the voltage-sourced converter under unbalanced grid conditions[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1620–1629. DOI:10.1109/TPWRD.2006.874641 |
| [14] |
胡书举, 李建林, 许洪华.
适用于直驱式风电系统的Crowbar电路分析[J]. 电力建设, 2007, 28(9): 44–47.
HU Shuju, LI Jianlin, XU Honghua. Analysis of crowbar circuits used in direct-drive WTG systems[J]. Electric Power Construction, 2007, 28(9): 44–47. (in Chinese) |
| [15] | Nian H, Liu J, Zhou P, et al.Improved control strategy of an active crowbar for directly-driven PM wind generation system under grid voltage dips[C]//International Conference on Electrical Machines and Systems, Wuhan, China, 2008:2294-2298. |
| [16] | Yuan X B, Wang F, Boroyevich D, et al. DC-link voltage control of a full power converter for wind generator operating in weak-grid systems[J]. IEEE Transactions on Power Electronics, 2009, 24(9): 2178–2192. DOI:10.1109/TPEL.2009.2022082 |
 2013, Vol. 36
2013, Vol. 36

