复杂型面零件的高速、高质量加工控制和无后续光整加工,对航空、宇航、模具等制造业具有特别重要的现实意义。传统的数控系统只支持直线、圆弧和螺旋线插补,而CAM系统必须根据设定的误差要求,目前只有FANUC、SIEMENS、和FIDIA等少数高档数控系统能支持用参数曲线表示的刀具路径离散成微小直线段和圆弧段,在CNC领域,复杂型面的应用却相对滞后。为此,国内外学者通过研究数控系统中的曲线曲面直接插补技术来克服传统加工方式的缺陷,提高加工效率和精度。为保证加工误差在允许范围内,Yeh等[1-3]提出了限定弦高误差的加工速度自适应插补算法,Tikhon等[4-6]提出了恒定切削率的加速度自适应算法,但加工速度的变化,有可能导致过切或欠切,破坏加工精度。为了克服这些缺陷,学者提出在曲率变化快的区域进行定位和加减速处理,以及将速度修整算法引入加减速处理,但是这些加减速过程中存在加速度突变,容易导致机床产生振动。最近出现了一些关于NURBS曲线曲面[7-8]的直接插补算法,但计算繁琐,需要较长的插补时间,占用内存空间多,难以实现NURBS曲线的快速实时插补。Shpitalni等[9]根据一阶Taylor展开式近似计算插补点,提出了加工速度恒定的参数曲线插补算法,此法计算量少,但误差较大。Yang等[10]在此基础上采用二阶Taylor展开式计算插补点,提高了逼近精度,但计算量有所增加,而且两者均未考虑误差控制。
为改善上述状况,在上述研究的基础上,通过比较一阶Taylor展开式插补算法、二阶Taylor展开式插补算法和迭代算法,提出了一种迭代算法技术引入数控系统中,实现了进给速度的精确控制。
1 曲线实时插补原理数控加工中,刀具沿加工路径方向运动的速度称为进给速度。几何造型中曲线/曲面可用参数方程表示,曲线的每一个坐标可以独立表达为
| $ C\left( u \right) = x\left( u \right)i + y\left( u \right)j + z\left( u \right)k, $ | (1) |
式中u为参数,通常0≤u≤1。当前插补点为ui,下一个插补点ui+1,瞬时插补进给速度为Vrefi,插补周期为T。理想情况下有
| $ \left\{ \begin{array}{l} {u_{i + 1}} = {u_i} + \Delta {u_i};\\ \left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\| = {V_{{\rm{refi}}}} \times T;\\ \left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\| \approx \int\limits_{{u_i}}^{{u_{i + 1}}} {\left\| {C\left( {{u_i}} \right)} \right\|{\rm{d}}u} 。\end{array} \right. $ | (2) |
如何实时准确地计算出下一个插补点ui+1=ui +Δui是插补算法的关键,曲线为自由曲线且其“参数—弧长”呈非线性关系,数控插补时插补点计算时分成一个插补周期获得较为精确的解析解,只能有近似解ui+1逼近真值解ui+1*,满足‖C(ui+1*)-C(ui)‖≈‖C(ui+1)-C(ui)‖,瞬时进给速度Vrefi无法准确达到,实际插补速度为
| $ {V_i} = \left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|/T。$ | (3) |
实际插补进给速度波动
| $ \Delta {V_i} = {V_{{\rm{refi}}}} - {V_i}, $ | (4) |
| $ \Delta {V_i} = {V_{{\rm{refi}}}} - \left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|/T。$ | (5) |
瞬时插补段速度波动率为
| $ \begin{array}{l} {\sigma _{{v_i}}} = \frac{{\Delta {V_i}}}{{{V_{{\rm{refi}}}}}} \times 100\% = \\ \;\;\;\;\;\;\;\;\left[ {1 - \frac{{\left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|}}{{T \times {V_{{\rm{refi}}}}}}} \right] \times 100。\end{array} $ | (6) |
已经理论计算传统圆弧插补算法,在圆心角为1°时,δVi =1.2×10-3%。正常插补时,Δu≪1°,速度波动几乎可以忽略。曲线插补与圆弧插补不同,其插补参数与曲线弧长呈非线性关系,Bedi [11]提出了等距离参数的参数曲线实时插补算法,即每个插补周期的插补参数增量Δu相同,但不同插补点内对应的弧长变化很大,造成较大的瞬时插补速度起伏波动。这种波动无法保证加工精度,甚至无法加工。
曲线实时插补时,为获得好的加工效果,通过速度规划方法,如S型加减速规划,“前瞻”速度处理,优化速度规划等,给出理想的刀具进给速度。依据瞬时进给速度Vrefi,精确计算下一个插补点ui+1,将实时插补进给速度波动率δVi控制在理想的范围内。
2 曲线实时插补进给速度控制方法曲线插补时,下一插补点应尽量减小δVi为目标,比较有影响的是有一阶Taylor展开法[12-13],二阶Taylor展开法[7]、预测修正迭代法[8, 15]、Taylor展开误差修正法[15]等。下面对前4种算法原理做简要介绍和对比。
2.1 常规插补算法 2.1.1 一阶Taylor展开法曲线C(u)的参数u为时间t的连续函数u(t),
| $ {u_{i + 1}} = {u_i} + \frac{{{V_{{\rm{refi}}}}T}}{{{{\left\| {{\rm{d}}C\left( u \right)/{\rm{d}}t} \right\|}_{u = {u_i}}}}}, $ | (7) |
dC(u)/dt={dx(u)/dt,dy(u)/dt,dz(u)/dt}=(x′,y′,z′),因此
| $ {u_{i + 1}} = {u_i} + \frac{{{V_{{\rm{refi}}}}T}}{{\sqrt {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2} + {{\left( {z'} \right)}^2}} }}。$ | (8) |
因为参数点由ui+1代入参考曲线方程求得,参考点总是在曲线上,故没有位置误差,但存在有Vi ≠ Vrefi,对曲线半径ρ较大的曲线δVi<5%,但ρ较小的曲线(如ρ<5 mm),该插补算法δVi较大了,不再适用,采用二阶Taylor展开法。
2.1.2 二阶Taylor展开法二阶Taylor展开法为
| $ \begin{array}{l} {u_{i + 1}} = {u_i} + \frac{{{V_{{\rm{refi}}}}T}}{{\left\| {{\rm{d}}C\left( u \right)/{\rm{d}}t} \right\|}} - \\ \;\;\;\;\;\;\;\;\;\frac{{\left( {TV} \right)_{{\rm{refi}}}^2\left| {{\rm{d}}C\left( u \right)/{\rm{d}}u \times {{\rm{d}}^2}C\left( u \right)/{\rm{d}}{u^2}} \right|}}{{\left\| {{\rm{d}}c\left( u \right)/{\rm{d}}t} \right\|_{u = {u_i}}^4 \times 2}}, \end{array} $ | (9) |
因此有
| $ \begin{array}{l} {u_{i + 1}} = {u_i} + \frac{{{V_{{\rm{refi}}}}T}}{{\sqrt {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2} + {{\left( {z'} \right)}^2}} }} - \\ \;\;\;\;\;\;\;\;\;\;\frac{{{{\left( {{V_{{\rm{refi}}}}T} \right)}^2}\left( {x'x'' + y'y'' + z'z''} \right)}}{{2{{\left( {{{\left( {x'} \right)}^2} + {{\left( {y'} \right)}^2} + \left( {z'} \right)} \right)}^2}}}。\end{array} $ | (10) |
利用改进的插补算法,进给速度误差明显减小,但计算量激增。
2.1.3 预测修正迭代法在一阶Taylor展开法的基础上进行修正,为解决计算量大,有
| $ {u_{i + 1}} = {u_i} + {V_{{\rm{refi}}}}T/{\left\| {{\rm{d}}C\left( u \right)/{\rm{d}}\left( u \right)} \right\|_{u = {u_i}}} + \varepsilon \left( {{u_i}} \right), $ | (11) |
式中ε(ui)的计算量也较大。以上3种算法中刀具瞬时插补路径仍是微线段,而非弧线段瞬时速度波动率较大,仍无法避免。
2.2 迭代插补算法对于曲线C(u),当插补弦长VrefiT和当前插补点ui给定时,满足式(3)条件的曲线向前点,参数ui+1即为下一插补点
| $ \left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\| = {V_{{\rm{refi}}}}T。$ | (12) |
通常情况下,满足式(12)的精确度ui+1,只能获得近似解,近似解与精确解间差异即为实际插补速度波动的根本原因。
2.2.1 迭代式的确定设当前插补点的参数为ui,下一个插补点为ui+1,构造函数F(ui+1)为
| $ F\left( {{u_{i + 1}}} \right) = \left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\| - {V_{{\rm{refi}}}}T。$ | (13) |
插补速度波动控制问题为:对于函数F(ui+1)解参数ui+1*(真值)。满足
| $ F\left( {u_{i + 1}^ * } \right) = 0。$ | (14) |
采用迭代法解方程(14),标准的迭代公式[9]为
| $ {u_{i + 1}} = {u_i} + F\left( {{u_i}} \right)/F'\left( {{u_i}} \right), $ | (15) |
F(ui)的一阶求导为
| $ F'\left( {{u_i}} \right) = {\rm{d}}\left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|/{\rm{d}}u, $ | (16) |
对应笛卡儿坐标系
| $ \begin{array}{l} F'\left( {{u_{i + 1}}} \right) = \left[ {\left( {X\left( {{u_{i + 1}}} \right) - X\left( {{u_i}} \right)} \right)\mathit{\boldsymbol{X'}}\left( {{u_{i + 1}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {Y\left( {{u_{i + 1}}} \right) - Y\left( {{u_i}} \right)} \right)\mathit{\boldsymbol{Y'}}\left( {{u_{i + 1}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {Z\left( {{u_{i + 1}}} \right) - Z\left( {{u_i}} \right)} \right)\mathit{\boldsymbol{Z'}}\left( {{u_{i + 1}}} \right)} \right]/\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|} \right]。\end{array} $ | (17) |
令
| $ \begin{array}{l} \overline {{\mathit{\boldsymbol{E}}_{{u_{i + 1}}}}} = \left\{ {\frac{{X\left( {{u_{i + 1}}} \right) - X\left( {{u_i}} \right)}}{{{{\left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|}^\prime }}},} \right.\\ \;\;\;\;\;\;\;\;\;\;\frac{{Y\left( {{u_{i + 1}}} \right) - Y\left( {{u_i}} \right)}}{{{{\left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|}^\prime }}},\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{{Z\left( {{u_{i + 1}}} \right) - Z\left( {{u_i}} \right)}}{{{{\left\| {C\left( {{u_{i + 1}}} \right) - C\left( {{u_i}} \right)} \right\|}^\prime }}}} \right\}, \end{array} $ |
则式(17)可重写为
| $ \begin{array}{*{20}{c}} {F'\left( {{u_{i + 1}}} \right) = \overline {{\mathit{\boldsymbol{E}}_{u + 1}}} \times \overline {{{\mathit{\boldsymbol{C'}}}_{u + 1}}} ,}\\ {\overline {{{\mathit{\boldsymbol{C'}}}_{{u_{i + 1}}}}} = \left( {\mathit{\boldsymbol{X'}}\left( {{u_{i + 1}}} \right),\mathit{\boldsymbol{Y'}}\left( {{u_{i + 1}}} \right),\mathit{\boldsymbol{Z'}}\left( {{u_{i + 1}}} \right)} \right),} \end{array} $ | (18) |
式中,构造函数F′(ui+1)等于弦长单位矢量
| $ {u_{i + 1}} = {u_i} - {\left( {\overline {{\mathit{\boldsymbol{E}}_{{u_{i + 1}}}}} \times \overline {{\mathit{\boldsymbol{C}}_{{u_i}}}} } \right)^{ - 1}}F\left( {{u_i}} \right), $ | (19) |
C(u)为正则参数曲线,具有连续可导,超线性收敛[9]。
2.2.2 初值的确定为避免速度波动,下一步理想的插补点C(ui+1*)应在弦长VrefiT处,弦长很小,即VrefiT≪1,则可用弧长表示弦长:
| $ {V_{{\rm{refi}}}} \times T \approx \int\limits_{{u_i}}^{u_{i + 1}^ * } {\left\| {C'\left( u \right)} \right\|{\rm{d}}u} , $ | (20) |
初值u0选取尽量接近其真值ui+1*,则
| $ {u_0} = {u_i} + {V_{{\rm{refi}}}}T/\left\| {C'\left( {{u_i}} \right)} \right\|, $ | (21) |
即为迭代初值计算公式。
2.2.3 终止条件迭代算法满足|ui+1-ui|≤ε,ε为迭代结果误差上限,也可用进给速度波动率上限δ为终止条件|δvi|≤δ,δvi由式(6)计算。还应对迭代次数设立最大上限N,与ε或δ指标联合使用。
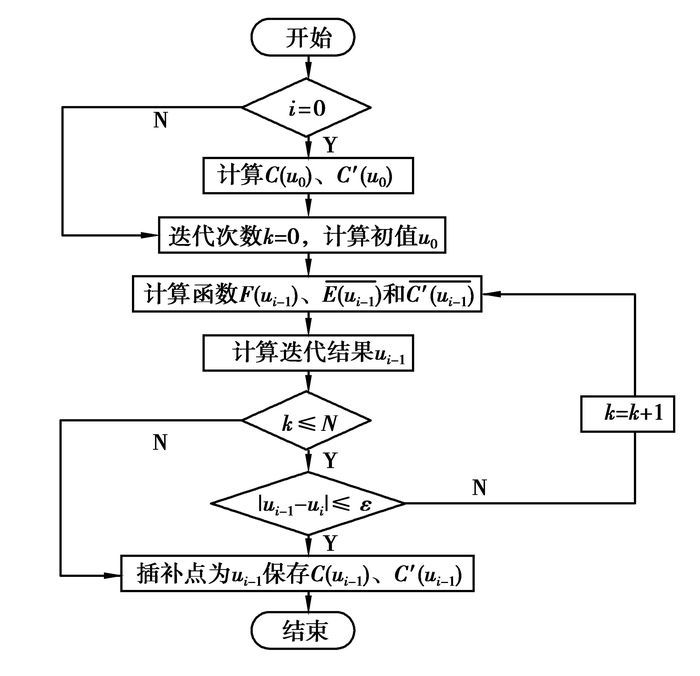
2.2.4 算法流程对于曲线C(u),设最初点为u0当前插补点参数为ui,下一插补点为ui+1,插补周期为T,瞬时插补进给速度为Vrefi,预设最大迭代次数为N次,设定插补参数迭代精度ε。则计算下一个理想插补点参数ui+1的计算流程为图 1所示。
|
图 1 迭代插补算法流程图 |
当插补点参数计算迭代结束时,由于ui+1已经求出的C(ui+1)、C′(ui+1)可直接用于下一个插补周期的迭代计算。因此采用迭代算法可有效减少计算量。一次迭代算法的计算量与一阶Taylor展开法相当,可以获得较高的控制精度,具有以下优点:采用主动控制方式,实时插补速度波动率可控;收敛速度快;计算量小,控制精度高;与其他算法容易兼容。
3 算例仿真及分析 3.1 算例仿真由于Taylor展开在参数曲线实时插补算法中应用广泛,以二阶Taylor展开法作为参照,验证迭代算法特征的正确性和有效性。迭代算法终止条件误差上限ε为0,插补周期T=0.001 s,进给速度Vrefi(u)=100 mm/s。
算例1
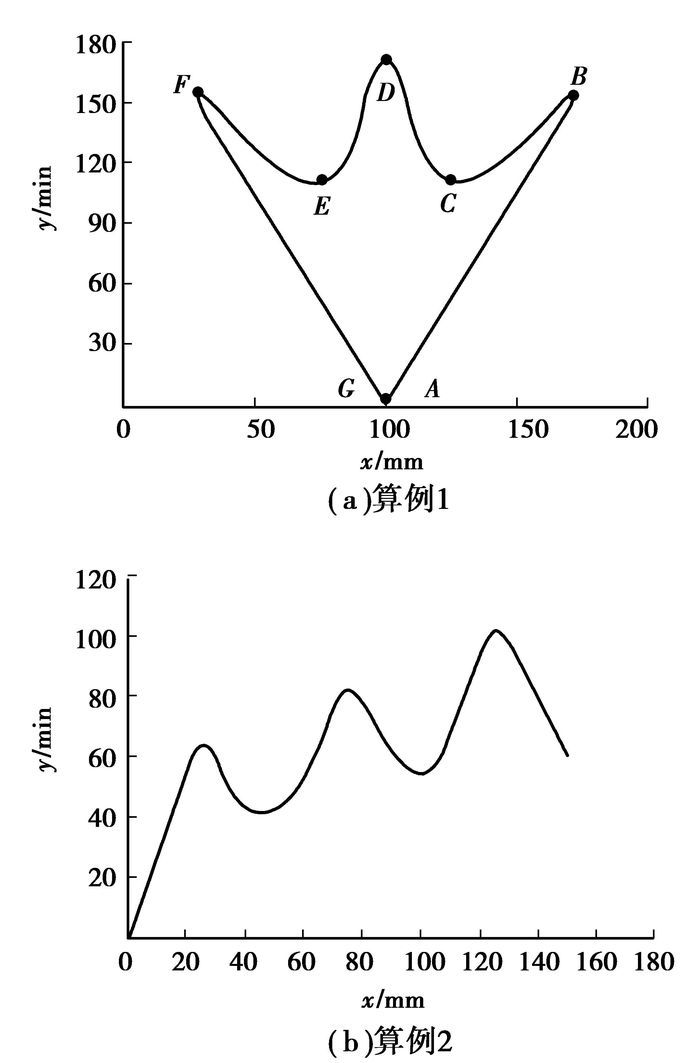
迭代次数N=1,见图 2(a):控制点的坐标(单位:mm)(100,0)(200,200)(120,80)(100,200)(80,80)(0,200)(200,0);
|
图 2 具体算例的曲线轮廓 |
各控制点的权因子均为1;
节点矢量(0,0,0,0.2,0.4,0.6,0.8,1,1,1)。
算例2
迭代次数N=2,见图 2(b):控制点的坐标为(0,0)(25,70)(50,20)(75,90)(100,40)(125,110)(150,60);
权因子分别为(1,25,25,25,25,25,1);
节点矢量为(0,0,0,0.15,0.48,0.56,0.72,1,1,1)。
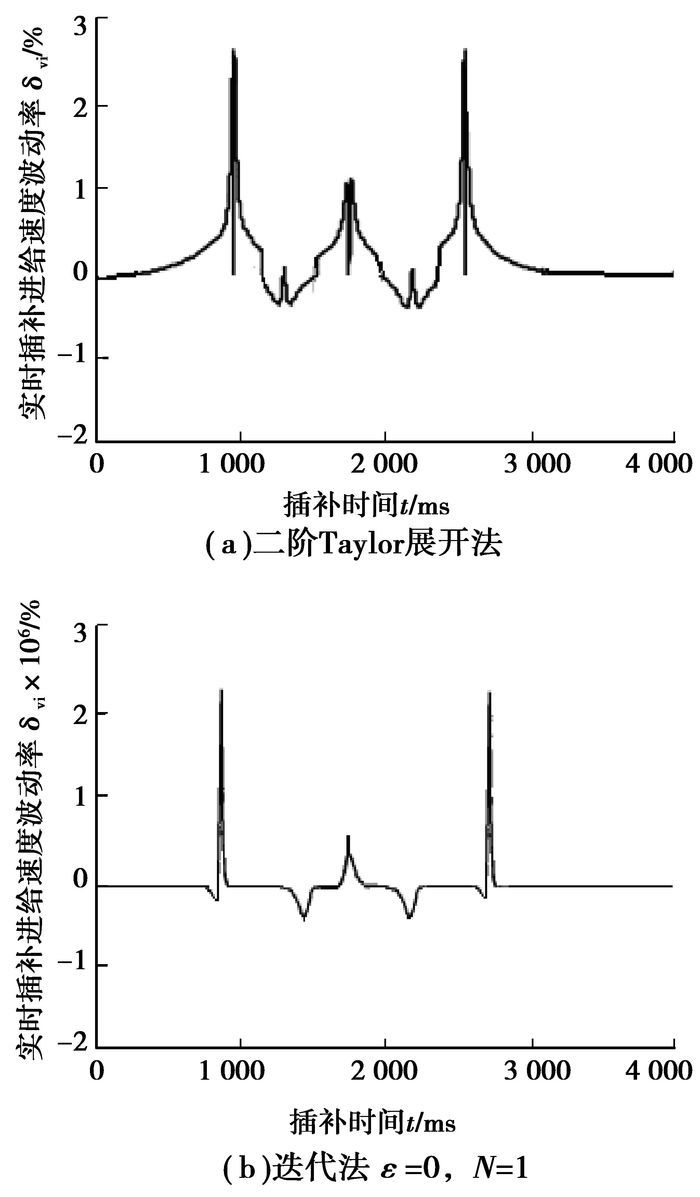
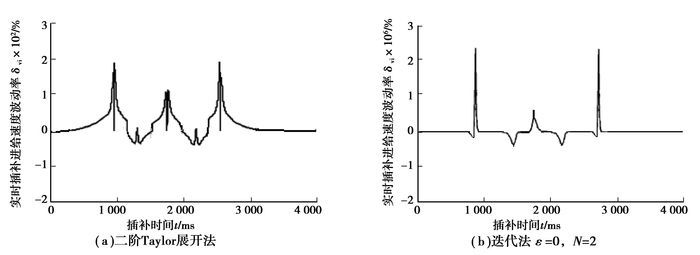
算例1对比结果见图 3,算例2对比结果见图 4(a)和图 4(b)。
|
图 3 算例1的不同方法下实时插补速度控制效果对比(曲线轮廓见图 2(a)) |
|
图 4 算例2的不同方法下实时插补速度控制效果对比 |
从仿真实验结果来看,2组仿真实验的“时间-速度波动率”曲线分别见图 3和图 4,实验结果见表 1。
| 表 1 不同实时插补进给速度控制方法对比结果统计 |
从图 3二阶Taylor展开法和迭代法(ε=0,N=1)尽管运算量相当,但迭代法的进给速度控制精度却提高了很多速度波动率由2.61%提高到2.48×10-6%,速度波动率降低至原来1/106。从图 4看,二阶Taylor展开法和迭代法(ε=0,N=2)插补效果比,由于迭代法运算量增加了1倍,但速度波动率由1.93×10-2%提高到2.36×10-8%,速度波动率也降低至原来1/106。进给速度波动率和计算量都有很大差距。二阶Taylor展开法比迭代法1次迭代计算量大,且波动率大,二阶Taylor展开法计算与迭代法迭代2次计算量相当,但后者的波动率最低;迭代法1与迭代法2比较,由于迭代次数增加为2时,速度波动率提高了105倍。因此迭代算法能够比较精确的控制数控系统的各运动轴的速度,获得较好的速度波动控制效果。各项对比结果见表 1。
4 结论实现曲线插补的难点在于曲线所具有的有理形式分段参数方程使曲线的轨迹及其导数、曲率等计算异常繁琐,给算法实现的实时性带来严重影响,高速精密加工要求CNC插补周期很小,这一问题尤为突出。文中提出的迭代算法,通过设定终止条件以合理的近似计算等措施,有效地简化了插补过程的轨迹计算,避免了对曲线的直接求导和曲率半径等复杂计算,确保了插补的良好实时性。
文中提出的一种新型迭代插补算法,简化了曲线曲面的加工编程,该算法对插补段弦长的逼近,更符合数控插补本质,获得了很好的进给速度控制效果。
| [1] | Yeh S S, Hsu P L. Adaptive-feedrate interpolation for parametric curves with a confined chord error[J]. Computer-Aided Design, 2002, 34(3): 229–237. DOI:10.1016/S0010-4485(01)00082-3 |
| [2] | Yong T, Narayanaswami R. A parametric interpolator with confined chord errors, acceleration and deceleration for NC machining[J]. Computer-Aided Design, 2003, 35(13): 1249–1259. DOI:10.1016/S0010-4485(03)00043-5 |
| [3] | Nam S H, Yang M Y. A study on a generalized parametric interpolator with real-time jerk-limited acceleration[J]. Computer-Aided Design, 2004, 36(1): 27–36. DOI:10.1016/S0010-4485(03)00066-6 |
| [4] | Tikhon M, Ko T J, Lee S H, et al. NURBS interpolator for constant material removal rate in open NC machine tools[J]. International Journal of Machine Tools & Manufacture, 2004, 44(2/3): 237–245. |
| [5] | Lin M T, Tsai M S, Yau H T. Development of a dynamics-based NURBS interpolator with real-time look-ahead algorithm[J]. International Journal of Machine Tools & Manufacture, 2007, 47(15): 2246–2262. |
| [6] | Tsai M S, Nien H W, Yau H T. An integrated look-ahead dynamic interpolator for NURBS curve[C]//Proceedings of the 200746th IEEE Conference on Decision and Control, December 12-14, 2007, New Orleans, LA. Piscataway:IEEE Press, 2007:1868-1873. |
| [7] | 施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 高等教育出版社, 2001. |
| [8] |
邱志平, 祁武超.
配点型区间有限元法[J]. 力学学报, 2011, 43(3): 496–504.
QIU Zhiping, QI Wuchao. Collocation interval finite element method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 496–504. DOI:10.6052/0459-1879-2011-3-lxxb2010-382 (in Chinese) |
| [9] | Shpitalni M, Koren Y, Lo C C. Real-time curve interpolators[J]. Computer-Aided Design, 1994, 26(11): 832–838. DOI:10.1016/0010-4485(94)90097-3 |
| [10] | Yang D C H, Kong T. Parametric interpolator versus linear interpolator for precision CNC machining[J]. Computer-Aided Design, 1994, 26(3): 225–234. DOI:10.1016/0010-4485(94)90045-0 |
| [11] | Bedi S, Ali I, Quan N. Advanced interpolation techniques for CNC machines[J]. ASME Journal of Engineering for Industry, 1993, 115: 329–336. |
| [12] |
沈斌, 欧阳华兵, 闫广超.
一种基于反馈补偿的参数曲线数控插补算法[J]. 机械工程学报, 2010(15): 136–141.
SHEN Bin, OUYANG Huabing, YAN Guangchao. A CNC interpolation algorithm for parametric curves based on feedback compensation[J]. Chinese Journal of Mechanical Engineering, 2010(15): 136–141. (in Chinese) |
| [13] |
陈恩伟, 陆益民, 刘正士, 等.
Taylor展开的线性时变系统参数辨识及误差分析[J]. 机械工程学报, 2011, 47(7): 90–96.
CHEN Enwei, LU Yimin, LIU Zhengshi, et al. Parameter identification and error analysis of linear time varying system based on Taylor expansion[J]. Chinese Journal of Mechanical Engineering, 2011, 47(7): 90–96. (in Chinese) |
| [14] |
罗福源, 游有鹏, 尹涓.
NURBS曲线S形加减速双向寻优插补算法研究[J]. 机械工程学报, 2012, 48(5): 147–156.
LUO Fuyuan, YOU Youpeng, YIN Juan. Research on the algorithm of NURBS curve bidirectional optimization interpolation with S-type acceleration and deceleration control[J]. Chinese Journal of Mechanical Engineering, 2012, 48(5): 147–156. (in Chinese) |
| [15] | Liu Y, Li H, Wang Y Z. Realization of a 5-axis NURBS interpolation with controlled angular velocity[J]. Chinese Journal of Aeronautics, 2012, 25(1): 124–130. DOI:10.1016/S1000-9361(11)60370-1 |
 2013, Vol. 36
2013, Vol. 36

