2. 湖南工业大学, 湖南 株洲 412007;
3. 一汽-大众汽车有限公司, 长春 130011
2. Hunan University of Technology, Zhuzhou, Hunan 412007, China;
3. FAW-Volkswagen Automotive Co., Ltd., Changchun 130011, China
现在大多数轿车都安装了空调系统,这不仅提高了汽车的舒适性,也提高了汽车的安全性能。设计汽车空调系统时,需要考虑很多因素[1]:乘员舱内乘客头部位置的风速要均匀、平稳,气流流速大致稳定在0.15~0.40 m/s之间;对于仪表板处驾驶员侧的风量比重应比副驾驶一侧稍大,大约占总共风量的52%左右;同时各个出风口风速差不应该超出2 m/s的范围,否则就会出现乘员舱内温度场、速度场分布不均匀,产生旋涡,不利于乘员舱内空气更新。其中,汽车空调的送风风道是汽车空调系统中重要的部件之一,其设计水平直接影响车内气流组织的合理性,从而影响乘员的热舒适性。对空调风道进行风量分析,评价空调系统设计是否合理,对提高乘员的热舒适性具有非常重要的工程意义[2]。
目前,随着计算机和数值技术的快速发展,通过对空调风道中气流的流动进行CFD仿真分析,进而对风道系统提出改进措施。利用CFD方法进行乘员舱热舒适性的研究也较多。2007年,江淮汽车公司的霍长宏、刘江波等[3]用CFD方法对某轻卡驾驶室除霜风道出口流量分配进行了分析,同时对风道结构进行了改进。2008年,上海交大的吴金玉、陈江平[4]通过对暖通空调(HVAC)及风道内部场的CFD分析,考察了风道内部结构对风量分配和送风量的影响,并提出了改进方法。文献[5]利用CFD分析了HVAC内气流的流动,并考虑了3种模式:吹面模式、除霜模式、吹脚模式。2010年,江淮汽车公司的陶其铭、许至宝等[6]运用CFD方法对某款汽车空调除霜风道内部流动进行了分析,并对其内部扰流板结构进行了改进设计,使得除霜风道各出风口分风比较为合理。2011年,上海工程技术大学的杨国平等[7]借助CFD方法建立了某轿车风道模型,并通过改进中央风道的性能,使各出风口的均匀性得到了提高。但在前人的研究中,对空调风道系统进行改进设计时,大多是对风道系统进行了结构上的改进,而在对乘员舱的热舒适性进行仿真分析时没有把整个空调系统考虑在内。基于此,文中在改进空调风道系统时,通过实验设计DOE(design of experiment)方法选取40个样本点,建立了三阶响应面模型,然后利用遗传算法对该响应面模型进行优化设计[8]。将空调系统和乘员舱作为一个整体,加入驾驶员模型,综合考虑乘员舱的热舒适性。
1 CFD模型及计算方法 1.1 数学模型空调风道内空气的湍流流动采用不可压缩流体的k-ε RNG湍流模型描述。在对k-ε RNG湍流模型方程进行推导时,必须对雷诺应力做出某种假定,在大量的实验基础上推导出了雷诺应力方程[9]为
| $\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} + \rho \varepsilon ,$ | (1) |
| $\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\alpha \varepsilon {\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{{C_{1\varepsilon }^*\varepsilon }}{k}{G_k} - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k},$ | (2) |
式中:ρ是流体密度;k为湍流动能;ε为湍流动能耗散率;Gk是由平均速度梯度引起的湍动能k的产生项;μeff为湍流有效粘性系数;αk、αε、Cμ、C1ε、C2ε、η0、β为经验常数。具体数值见表 1。
| 表 1 湍流数学模型中的常数 |
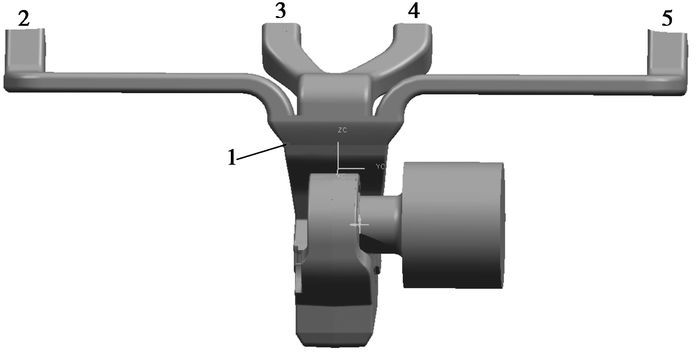
研究采用带有离心通风机的4出口式标准空调风道模型,风道结构基本为对称设计。为了便于后续的计算分析,在UG 4.0中建立本模型时,设置了5个监控面分别用来监测空调风道的总出风量以及4个出风口的出风量,逐次将其标记为1、2、3、4、5,其中驾驶员在靠近5号风道侧(见图 1)。
|
图 1 带有离心通风机的空调风道UG模型 |
网格划分是运用前处理软件ICEM CFD 10.0完成的,由于最后需要的结果是风道系统整体运行时的各个出风口的出风量比例,所以对连接在一起的整个计算区域整体进行了网格划分,在划分网格时采用区域扩充法,在风道外部某些区域扩充计算区域,使整个计算区域尽量趋于规则[4](见图 2)。

|
图 2 全局网格划分示意图 |
计算采用商用软件Fluent V6为求解器,选用k-ε RNG湍流模型求解[10]。离心通风机叶片绕风机轴心旋转,叶片与风机壁面是相对运动的,在Fluent中可以通过多重参考系(MRF)模型和滑移网格来实现这种定轴旋转运动。多重参考系是将静止的区域采用静止的绝对坐标系,而旋转的区域采用旋转的相对坐标系,坐标系的旋转速度为叶片的旋转速度。2个区域的交界面处交换流动参数,保证交界面上的连续性。滑移网格则是将动静2个区域都采用静止的绝对坐标系,在计算时旋转区域的网格以叶片的角速度进行旋转。研究采用MRF来对风机叶片进行模拟,可以节省资源提高计算效率。具体边界条件设置如表 2所示。
| 表 2 边界条件设置 |
试验基于风量性能测试台,对原车空调系统进行出风口风量分布检测,此性能试验台被测风量范围为0~800 m3/h,测定精度可达3%,并满足标准QC/T 657—2000的要求。如表 3所示,为CFD仿真和试验原车空调系统各风道风量分配对比。
| 表 3 仿真和试验对比 |
由于风量泄漏等因素,所以试验时总出风口风量偏小。由仿真试验对比可知,CFD仿真的误差在5%以内,因此CFD仿真方法是可行的。
2 优化设计 2.1 设计变量研究利用UG4.0在空调风道里所加的导流片模型及决定其结构形状的3个关键尺寸如图 3所示。选取这3个尺寸变量为设计变量并将其参数化为:y为导流片距离风道中心线的距离、α为导流片的倾斜角、r为导流片的拐角半径。

|
图 3 导流片模型及设计参数示意图 |
采用DOE分析中的优化拉丁方法确定40组设计样本点,如表 4所示。
| 表 4 优化拉丁方法确定的样本点 |
在UG里面根据不同的样本点作出不同的导流片模型,将其导入ICEM CFD 10.0中进行网格划分,然后将网格文件导入Fluent求解器里计算得出40组样本数值。在进行双目标优化时,由于风量分配与总出风量这2个目标同等重要,所以配备了相同的权重,优化问题可以描述为
min f=ω1D1+ω2D2,
s.t. y∈[10 mm,80 mm],
α∈[20°,45°],
r∈[100 mm,200 mm]
式中:D1为驾驶员侧风量比重与52%的差值;D2为导流片施加前后空调出风口总出风量的差值,kg/s;ω1、ω2为权重系数,分别取为0.5,0.5。
2.2 遗传算法遗传算法是一种基于生物选择与进化的随机性搜索算法,它采用概率转移率,以一定的概率选择部分个体繁殖,选一些个体灭亡,从而将搜索引向解空间中最可能获得改进的区域。
遗传算法解决优化问题的稳定性和鲁棒性要好于常规优化算法,虽然这是以计算量大幅度增加为代价的,但随着计算机硬件技术的发展,这已不是制约因素。遗传算法的内在并行机制及其全局优化的特点适合于多目标优化问题的解决,特别是目标函数多、数学表达式非线性或者不明确、优化变量多、常规方法难以奏效的复杂场合[11]。
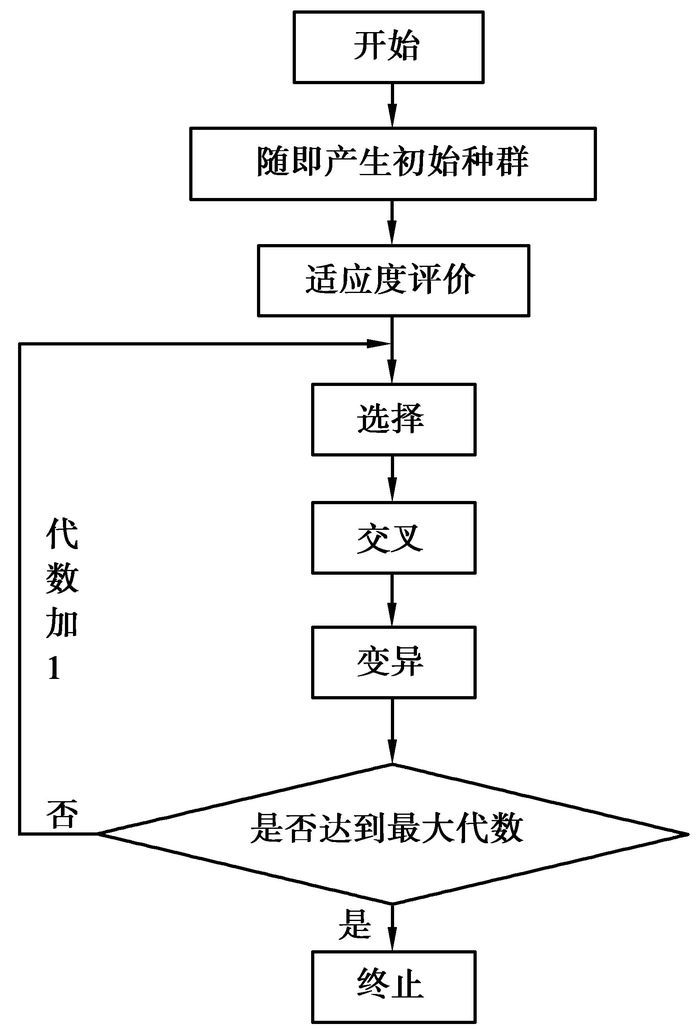
研究利用遗传算法进行优化设计的流程如图 4所示。
|
图 4 遗传算法优化设计流程图 |
通过计算出来的40组样本数值,运用最小二乘原理建立三阶响应表面模型,即关于y、α、r的一个3次多项式。
在得到响应表面后,需要对响应表面的拟合程度进行验证。可以通过方差分析中决定系数R2和调整的决定系数Radj2,来验证响应表面对响应量的拟合情况。决定系数R2和调整的决定系数Radj2为
| ${R^2} = \frac{{\sum\limits_{i = 1}^P {{{({{\hat y}_i} - {{\bar y}_i})}^2}} }}{{\sum\limits_{i = 1}^P {{{({y_i} - {{\bar y}_i})}^2}} }},$ | (3) |
| $R_{{\rm{adj}}}^2 = 1 - \frac{{\sum\limits_{i = 1}^P {{{({y_i}{{\hat y}_i})}^2}} \left( {P - 1} \right)}}{{\sum\limits_{i = 1}^P {{{({y_i} - {{\bar y}_i})}^2}} \left( {P - k - 1} \right)}},$ | (4) |
式中:P是设计点的个数;k是自由度,其值为调整参数的个数减1;yi,
根据式(3)和式(4),得到所建响应面模型的决定系数R2达到91.32%,调整的决定系数Radj2达到90.07%。由此可知,该模型对响应量达到了高度拟合,使用此近似模型来替代直接的CFD仿真计算是可行的。
3.2 优化结果分析采用遗传算法进行优化分析,设置初始种群个体数为30,其他默认为缺省参数(进化繁殖100代),最终得出模型最优解。根据最优点建立相应的UG模型进行CFD仿真计算,CFD计算得出的数值与近似模型得出的结果误差仅为-1.74%和-2.11%。具体见表 5所示。
| 表 5 最优点仿真值与近似模型响应值对比 |
优化后的空调风道系统,驾驶员侧出风口风量(即4、5号出风口)所占比重为51.298%,总出风口风量比之前减少0.000 92 kg/s,约1.2%,影响不大,故满足设计要求。具体如表 6所示。
| 表 6 优化前后出风量对比 |
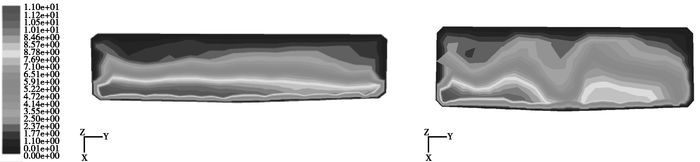
图 5和图 6是优化前后空调风道系统的速度云图及管道表面静压云图,从图中可以看出,原始空调风道由于离心通风机的影响,在副驾驶一侧,即2、3号风道侧的出风速度及管道表面静压都大于驾驶员一侧,导致空调出风量分配不均匀且驾驶员侧出风量比例过小;优化后由于导流片的作用,使得出风速度及表面静压较之前分配更均匀,从而空调出风量也更加均匀,并且驾驶员侧的出风量有大幅的增加。
|
图 5 优化前后进风口速度云图(左为原始) |

|
图 6 优化前后管道表面静压云图(左为原始) |
汽车乘员舱是一个微环境,所受的热源众多,而且太阳辐射分布不均,乘员舱内的温度与速度变化梯度大,热环境非常不均匀。因此本文中选择当量温度Teq, i作为热舒适性评价指标。当量温度Teq, i包括了传热、对流换热、热辐射以及太阳辐射对人体的影响。同时该评价标准也能反应出人体的不同部位对温度的敏感度。因此该评价标准非常适合汽车乘员舱的热舒适性研究。
将驾驶员人体分为16个节段,分别对人体不同节段进行热舒适性评价。Teq, i的计算公式为
| $\begin{array}{l} {T_{{\rm{eq}},{\rm{ }}i}} = {T_{s,{\rm{ }}i}} - \frac{{8.3v_{{\rm{air}},{\rm{ }}i}^{0.6}{S_i}({T_{s,{\rm{ }}i}} - {T_{a,{\rm{ }}i}})}}{{{h_{{\rm{cal}},{\rm{ }}i}}{S_i}}} - \\ \quad \quad \frac{{\sum\limits_n {\sigma {\varepsilon _i}} {f_{i,{\rm{n}}}}{S_i}(T_i^4 - T_n^4) - {Q_{{\rm{sol}}}}}}{{{h_{{\rm{cal}},{\rm{ }}i}}{S_i}}}, \end{array}$ |
式中:Teq, i为第i节段的当量温度;Ts, i为第i节段的表面温度,vair, i为第i节段周围的空气速度;Si为第i节段的表面面积,Ta, i为第i节段周围的空气温度;σ为斯蒂芬波尔兹曼;εi为第i节段的发射率;fi, n为第i节段对部件表面的角系数;Ti为第i节段的温度;Tn为汽车乘员舱内部件的温度;Qsol为人体得到的太阳辐射;hcal, i为在标准环境下感受器标定的第i节段的对流换热系数,i为人体的节段[14]。
4.2 热舒适性分析将优化前后的空调风道系统应用于乘员热舒适性分析[13-15],图 7是带有驾驶员人体模型及空调风道系统的整车模型。

|
图 7 带有人体模型的整车模型 |
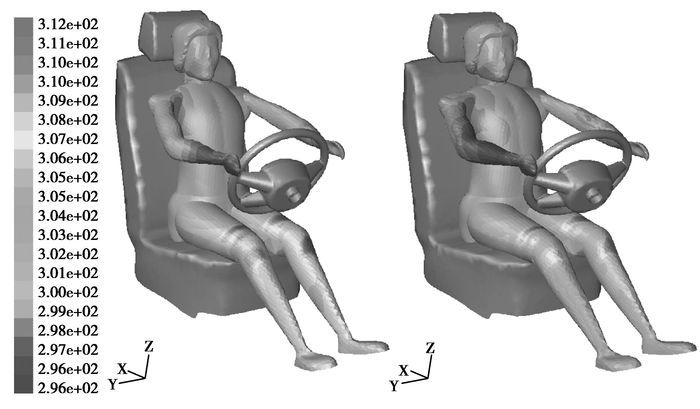
通过Fluent软件仿真得出人体表面温度分布云图,如图 8所示。可以看出,优化后由于驾驶员侧的冷风风量比重增大,所以驾驶员躯干部位的温度有所降低,人体散热效果得到了改善。图 9为人体各部位热舒适性示意图,与优化前相比,优化后人体各部位温度都有所降低,躯干部位温度大约下降1 ℃,腿部温度下降1~2 ℃。由此可以看出经过对空调风道的改进,人体热舒适性得到了改善。
|
图 8 优化前后人体表面温度分布云图(左为原始) |
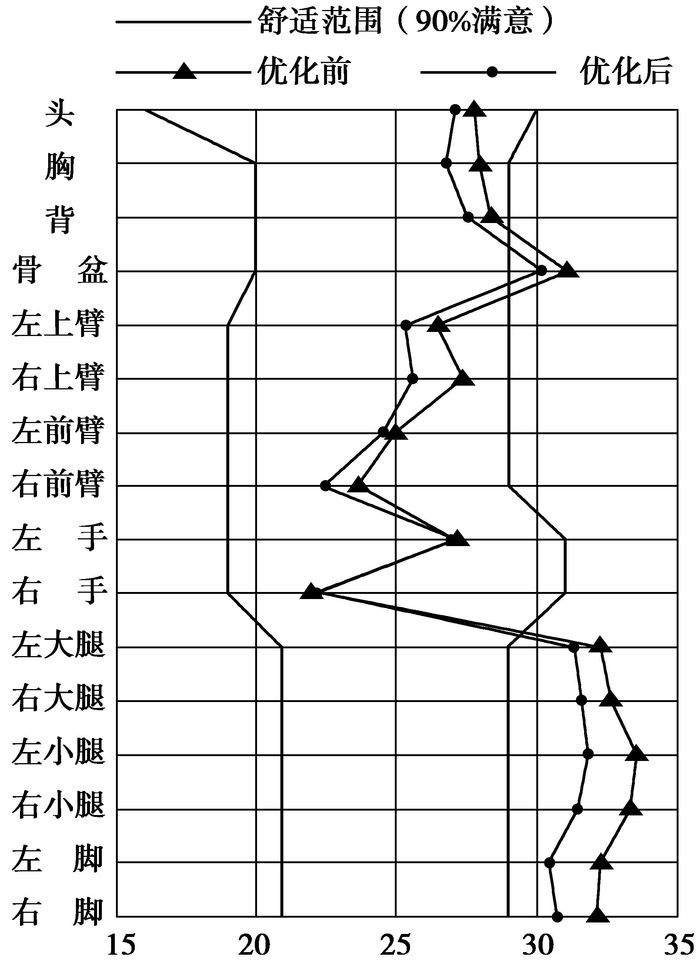
|
图 9 人体热舒适性示意图 |
在原有空调风道里加上一导流片,并将此导流片的3个结构尺寸参数化后定义为设计变量,通过DOE实验设计方法选取样本点建立近似模型并进行优化,并将优化后的风道系统应用于乘员热舒适性分析,驾驶员的热舒适性得到了明显的改善。
1) 建立的三阶响应面模型精度很高,可以代替实际的仿真计算分析,提高计算效率。
2) 利用遗传算法对建好的近似模型进行优化,得出最优解,并将其代入CFD仿真验算,误差很小。
3) 通过优化前后的对比分析,优化后驾驶员侧的风量比重达到了约51.3%,效果明显。
4) 将改进后的空调风道系统应用于驾驶员热舒适性分析,优化后驾驶员躯干部位温度有所降低,热舒适性得到了明显改善。
| [1] | 方贵银, 李辉. 汽车空调技术[M]. 北京: 机械工业出版社, 2003. |
| [2] | Chien C H, Jang J Y, Chen Y H, et al. 3-D numerical and experimental analysis for airflow within a passenger compartment[J]. International Journal of Automotive Technology, 2008, 9(4): 437–445. DOI:10.1007/s12239-008-0053-2 |
| [3] |
霍长宏, 刘江波, 俞燕.
CFD分析和模拟技术在某轻卡风道设计中的应用[J]. 合肥工业大学学报:自然科学版, 2007, 30(Sup1): 19–21.
HUO Changhong, LIU Jiangbo, YU Yan. The application of CFD analysis and simulation techniques in a light truck ventilation duct design[J]. Journal of Hefei University of Technology:Natural Science Edition, 2007, 30(Sup1): 19–21. (in Chinese) |
| [4] |
吴金玉, 陈江平.
汽车空调蒸发器总成及风道的数值研究[J]. 流体机械, 2008, 36(7): 59–62.
WU Jinyu, CHEN Jiangping. Numerical simulation of HVAC & vent in vehicle air conditioning system[J]. Fluid Machinery, 2008, 36(7): 59–62. (in Chinese) |
| [5] | Patidar A, Natarajan S, Pande M. CFD analysis and validation of an automotive HVAC system[C]//Proceedings of the SAE World Congress & Exhibition, April 20, 2009, Detroit, Michigan, United States.[S.l.]:SAE Technical Paper, 2009:2009-01-0535. |
| [6] |
陶其铭, 许志宝, 夏广飞.
汽车空调除霜风道分析及结构优化[J]. 合肥工业大学学报:自然科学版, 2010, 33(4): 498–500.
TAO Qiming, XU Zhibao, XIA Guangfei. Analysis and structure optimization for auto HVAC defrosting duct[J]. Journal of Hefei University of Technology:Natural Science Edition, 2010, 33(4): 498–500. (in Chinese) |
| [7] |
杨国平, 张缓缓, 朱法龙.
基于CFD汽车空调中央风道的改进设计[J]. 上海工程技术大学学报, 2011, 25(2): 108–111.
YANG Guoping, ZHANG Huanhuan, ZHU Falong. Improved design of car central air-conditioning duct system based on CFD[J]. Journal of Shanghai University of Engineering Science, 2011, 25(2): 108–111. (in Chinese) |
| [8] | 郭仁生. 基于MATLAB和Pro/ENGINEER优化设计实例解析[M]. 北京: 机械工业出版社, 2007. |
| [9] | Fluent Help[M]. 2005:273-301. |
| [10] |
谷正气, 孟庆超, 杨易, 等.
轿车室内流场的数值模拟研究[J]. 系统仿真学报, 2008, 20(7): 1700–1702, 1739.
GU Zhengqi, MENG Qingchao, YANG Yi, et al. Research on numerical simulation of air-flow field in car cabin[J]. Journal of System Simulation, 2008, 20(7): 1700–1702, 1739. (in Chinese) |
| [11] | Yücenur G N, Demirel N Ç. A new geometric shape-based genetic clustering algorithm for the multi-depot vehicle routing problem[J]. Expert Systems with Applications, 2011, 38(9): 11859–11865. DOI:10.1016/j.eswa.2011.03.077 |
| [12] | Basa D, Boyaci I H. Modeling and optimizationⅡ:comparison of estimation capabilities of response surface methodology with artificial neural networks in a biochemical reaction[J]. Journal of Food Engineering, 2007, 78(3): 846–854. DOI:10.1016/j.jfoodeng.2005.11.025 |
| [13] | Akyol S M, Kilic M. Dynamic simulation of HVAC system thermal loads in an automobile compartment[J]. International Journal of Vehicle Design, 2010, 52(1/2/3/4): 177–198. DOI:10.1504/IJVD.2010.029643 |
| [14] | Han T, Huang L. A sensitivity study of occupant thermal comfort in a cabin using virtual thermal comfort engineering[C]//Proceedings of the SAE 2005 World Congress & Exhibition, April 11, 2005, Detroit, Michigan, United States.[S.l.]:SAE Technical Paper, 2005:2005-01-1509. |
| [15] | Han T, Chen K. Assessment of various environment thermal loads on passenger compartment soak and cool-down analyses[C]//Proceedings of the SAE World Congress & Exhibition, April 20, 2009, Detroit, Michigan, United States.[S.l.]:SAE Technical Paper, 2009:2009-01-1148. |
 2013, Vol. 36
2013, Vol. 36

