2. 招商局重庆交通科研设计院有限公司, 重庆 400067
2. China Merchants Chongqing Communications Research & Design Institute Co., Ltd., Chongqing 400067, China
英国科学家Zienkiewicz于1975年首次提出在有限元计算中可以通过折减材料强度或增加材料容重来确定岩土结构的安全系数和极限荷载[1]。这一思想的提出,开辟了有限元极限分析法的思路,容重增加法和强度折减法为有限元极限分析法的2个分支方向。
中国以郑颖人、赵尚毅、栾茂田、宋二祥等为代表的一批学者做了大量的工作。通过对一些算例的计算分析,证明了有限元强度折减法计算边坡的安全系数及潜在破裂面位置与传统的方法基本一致[2-8]。
通过长期的经验总结,发现容重增加法计算的结果与理论解相差较大,因此目前容重增加法在工程中应用较少。笔者对容重增加法不能计算得到一些边坡的安全系数的原因做出过一些解释[9]。
传统的极限平衡方法是将土体的抗剪强度指标c、tanφ折减为c′、tanφ′使岩土达到极限稳定状态,即
| $ c' = \frac{c}{F},\tan \varphi ' = \frac{{\tan \varphi }}{F}, $ | (1) |
其中F为材料的强度折减系数。边坡一般情况下为剪切破坏,这种强度折减法只考虑了抗剪强度指标c、tanφ的折减,应为”抗剪强度折减法”。
然而,边坡的破坏不仅仅是剪切破坏,边坡的后缘往往会产生拉裂破坏。戴自航、刘志伟等对不考虑岩(土)体的张拉强度(认为土体抗拉强度为0)的边坡进行过稳定性分析,结果表明:材料的抗拉强度对边坡的稳定性有一定的影响[10]。
类比通过折减材料强度计算边坡安全系数的方法,郑颖人等利用有限元强度折减法对隧道结构的安全性做了一些开创性的研究,计算得到了一些隧道的“剪切破坏安全系数”,并指出隧道还存在1个“拉裂破坏的安全系数”[6-7, 11]。
显然隧道的破坏并非单纯的剪切破坏或者单纯的拉伸破坏,是2种破坏形式并存,因此以往的计算方法有待改进。
文中首先分析”抗剪强度折减法”在稳定性计算中存在的问题,然后提出改进的方法,最终选取4个有代表性的岩土结构模型(一般边坡、钟乳石、陡边坡、隧道),通过对比”抗剪强度折减法”和改进的强度折减法的计算结果来说明提出的强度折减方式计算的安全系数更合理,更有普遍适用性。
1 改进的强度折减法 1.1 岩(土)的破坏特征在常规三轴压缩状态下,岩石材料的脆性破坏只有剪切破坏形式[12],土体在压应力空间中也往往处于受剪破坏。
在出现了拉应力的情况下,可以认为当某一节点的最大拉应力大于岩石的抗拉强度时,此节点就破裂[13],对于土体也类似。
因此,可以认为岩(土)材料受压时由抗剪强度指标决定其是否破坏,受拉时由抗拉强度指标决定其是否破坏,即岩(土)材料具有张拉、剪切破坏的特征。
1.2 强度折减法存在的问题有限元强度折减法的实质是:在有限元计算中通过改变岩土材料强度参数的方法,迫使岩土结构达到濒临屈服的临界状态,从而获得原来状态强度参数的富裕程度,并通过安全系数来描述这一富裕程度的大小。
因此,在强度折减的过程中,须针对起作用的强度进行折减。如果结构破坏纯粹由抗剪强度引起,那么只需要进行抗剪强度折减;如果破坏纯粹由抗拉强度引起,那么应进行抗拉强度折减。
100多年来,无数试验和实际工程的应用表明,Mohr-Coulomb屈服准则能较好地拟合试验结果和可靠地应用于岩土工程实践。通常用于强度折减法中的Mohr-Coulomb屈服准则只有2个强度参数:粘聚力c和内摩擦角φ。
当σ1=σ2=0,σ3=-σt时,通过摩尔圆与直线相切就可以计算得到材料的单轴抗拉强度σt。
| $ {\sigma _t} = \frac{{2c}}{{\tan \varphi + \sqrt {1 + {{\tan }^2}\varphi } }}。$ | (2) |
抗剪强度参数按照式(1)折减后,单轴抗拉强度可以表示为
| $ {{\sigma '}_t} = \frac{{2c}}{{\tan \varphi + \sqrt {{F^2} + {{\tan }^2}\varphi } }}, $ | (3) |
其中F为抗剪强度折减系数,定义Ft为抗剪强度折减前后对应单轴抗拉强度的比值,于是,
| $ {F_t} = \frac{{{\sigma _t}}}{{{{\sigma '}_t}}} = \frac{{\tan \varphi + \sqrt {{F^2} + {{\tan }^2}\varphi } }}{{\tan \varphi + \sqrt {1 + {{\tan }^2}\varphi } }}。$ | (4) |
由式(4)知,在抗剪强度指标c、tanφ按式(1)折减过程中,由c和tanφ表示的抗拉强度σt并没有同等地减少。例如:φ=60°的材料,当折减系数F=10时,计算得到Ft=3.2。这说明当抗剪强度减少到为原来的1/10时,单轴抗拉强度仅仅减少到原来的1/3.2。因此,在强度折减后过高地估计了材料的抗拉性能。
当岩土材料出现三向拉应力时,三轴受拉的极限强度σtⅢ可以表示为
| $ \sigma _t^{{\rm{Ⅲ}}} = - \frac{c}{{\tan \varphi }} - \frac{{\frac{c}{F}}}{{\frac{{\tan \varphi }}{F}}} = \sigma _t^{{\rm{Ⅲ'}}}。$ | (5) |
可见,抗剪强度指标c、tan φ折减时,材料三轴受拉的极限强度σtⅢ不受折减系数的影响,强度指标折减前后的数值大小相等,这样也是对σtⅢ的过高估计。
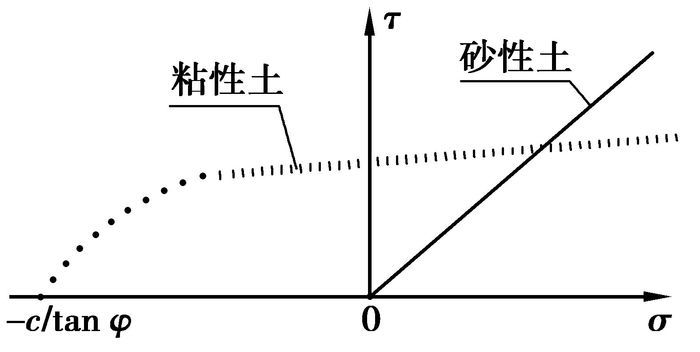
图 1为砂性土与粘性土在应力空间中的屈服面,可以看出,对于砂性土,不会出现拉应力,只能受剪破坏,按照以往的强度折减法计算的结果仍比较正确;对于粘性土,摩擦角很小,因此c/tan φ取值很大,若不考虑抗拉强度指标的修正,计算将产生非常大的偏差,这就是以往强度折减法对粘土边坡不适用的原因。
|
图 1 砂性土及粘性土的屈服面 |
以上分析说明,原有的强度折减法都在一定程度上高估了材料的抗拉强度,当抗拉强度对结构稳定性有帮助时,会对最终的计算结果产生一定的影响。对于满足Drucker-Prager屈服准则的岩土材料也会有类似的结论。因此有必要针对岩土张拉破坏的特征专门考虑抗拉强度的折减。
1.3 改进的强度折减法的提出岩石的抗拉强度比较低,一般为抗压强度的1/10[12];土体抗拉强度很低,一般为20~40 kPa。在很多情况下由Mohr-Coulomb屈服准则的强度参数c、tan φ确定的的岩(土)材料的抗拉强度值不符合事实,因此有人提出增加抗拉强度指标T对Mohr-Coulomb屈服准则进行拉伸截断[14]。
安全系数具有强度储备的含义。岩(土)材料的强度储备应包含抗剪强度储备和抗拉强度储备,所以在强度折减过程中应考虑抗拉强度指标和抗剪强度指标的折减。为了使材料的抗剪安全储备大小和抗拉安全储备大小都同等地减小,须满足抗拉强度指标与抗剪强度指标同等减少,即
| $ c' = \frac{c}{F},\tan \varphi ' = \frac{{\tan \varphi }}{F},T' = \frac{T}{F}。$ | (6) |
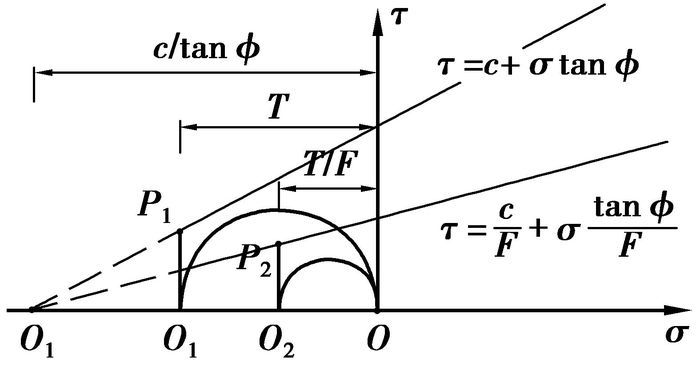
基于拉伸截断的Mohr-Coulomb屈服准则提出改进的强度折减法,称为“抗拉剪强度折减法”。可以推断,通过“抗拉剪强度折减法”计算得到的岩土结构安全系数更能表征结构安全储备的大小。“抗拉剪强度折减法”在折减前后的屈服面如图 2所示。
|
图 2 强度折减前后的屈服面 |
显然,有了抗拉强度T的限制,就能够有效地避免强度折减过程中对抗拉强度的高估。
下面通过4个算例模型来对比研究”抗剪强度折减法”和“抗拉剪强度折减法”的计算结果,说明新强度折减法在岩土工程中更有适用性。
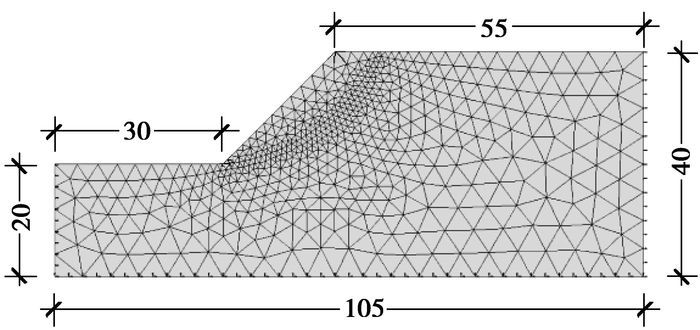
2 算例 2.1 一般边坡模型算例边坡模型如图 3所示。边坡坡度为45°,高20 m。土体材料为服从Mohr-Coulomb屈服准则与非关联流动法则(膨胀角ψ=0)的理想弹塑性材料,土的容重γ=20 kN/m3,粘聚力c=42 kPa,内摩擦角φ=17°,弹性模量E=100 MPa,泊松比υ=0.3。
|
图 3 一般边坡有限元计算模型(单位:m) |
用有限元强度折减法计算了”抗剪强度折减法”和“抗拉剪强度折减法”抗拉强度为0时的安全系数,并与传统方法对比,结果如表 1所示。可以看出,2种强度折减法计算结果一致,如果抗拉强度为不同的取值,计算结果在1.18~1.21之间。
| 表 1 算例的一般边坡安全系数 |
提取按“抗剪强度折减法”极限状态(F=1.21)的塑性区和受拉区云图,如图 4、图 5所示。从图中可以看出,塑性区的范围和受拉区的范围重叠的区域很小。所以边坡是受剪破坏位置的结构,其稳定主要取决于材料的抗剪强度。

|
图 4 一般边坡塑性区云图 |

|
图 5 一般边坡受拉区云图 |
整个结构如果以受剪破坏为主,只需要折减材料抗剪强度指标就能得到比较准确的解答,可以不进行抗拉强度的折减;如果考虑抗拉强度影响,采用“抗拉剪强度折减法”计算的结果仍然是比较准确可靠的。
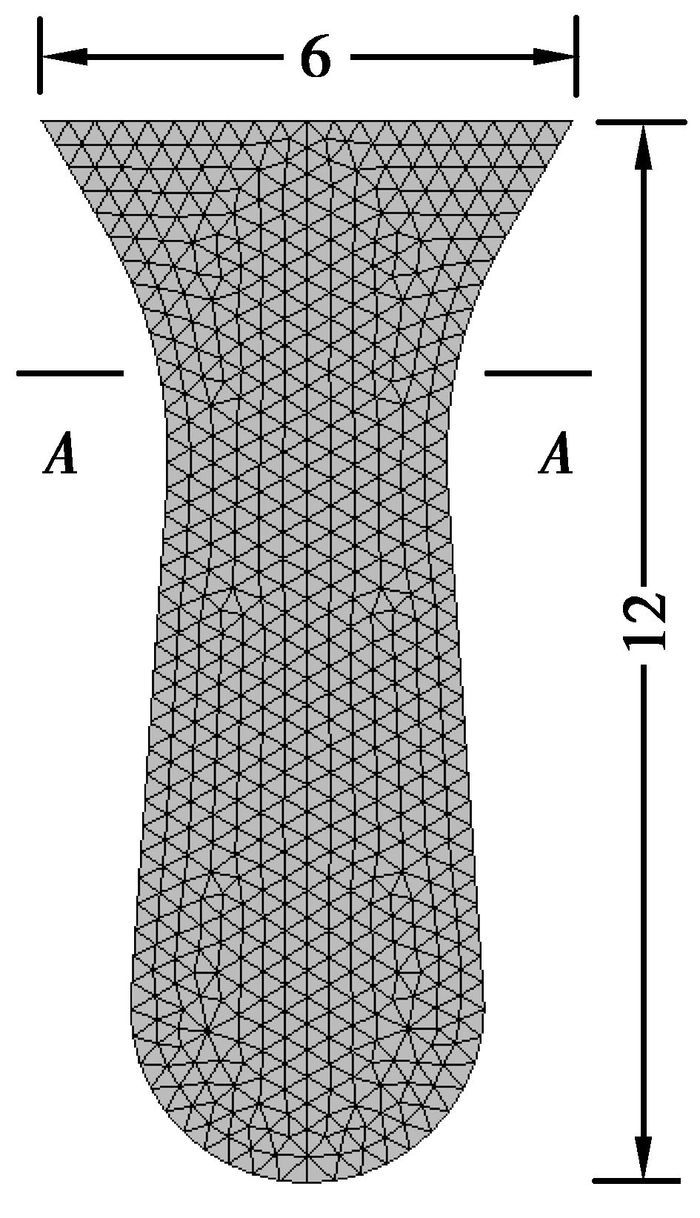
2.2 钟乳石模型算例钟乳石模型如图 6所示,岩石材料为服从Mohr-Coulomb屈服准则与非关联流动法则(膨胀角ψ=0)的理想弹塑性材料。容重γ=25 kN/m3,粘聚力c=1 600 kPa,抗拉强度T=600 kPa,内摩擦角φ=45°,弹性模量E=30 GPa,泊松比υ=0.26。
|
图 6 钟乳石有限元计算模型(单位:m) |
显然,钟乳石是纯粹受拉的结构,其稳定性取决于材料的抗拉强度。由材料力学的知识可知,算例钟乳石最薄弱、最容易发生破坏的位置显然应该在图 6中A-A截面的位置。
| 表 2 钟乳石安全系数 |
结果表明:只折减抗拉强度T和按照式(6)折减3个强度指标计算的结果一致,与材料力学解也一致。采用“抗剪强度折减法”按照式(1)折减强度计算的结果与以上3种方法的偏差较大。
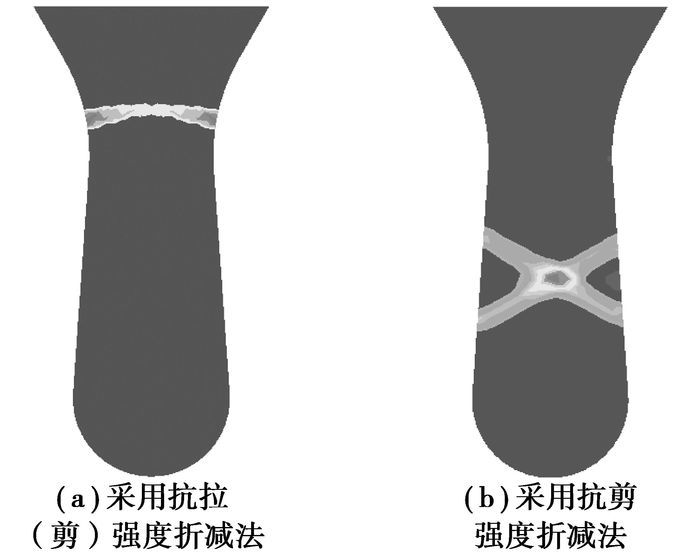
采用“抗拉强度折减”和“抗拉剪强度折减”计算得到的潜在破坏面的位置如图 7(a)所示,比较接近A-A截面位置;采用“抗剪强度折减法”计算得到的潜在破裂面的位置如图 7(b)所示,显然不正确。
|
图 7 钟乳石潜在破裂面 |
对于以受拉破坏为主的岩土结构,只要折减其抗拉强度指标就能得到比较准确的解答,采用“抗拉剪强度折减法”计算的结果也是正确的,采用“抗剪强度折减法”计算得到的结果是不正确的。
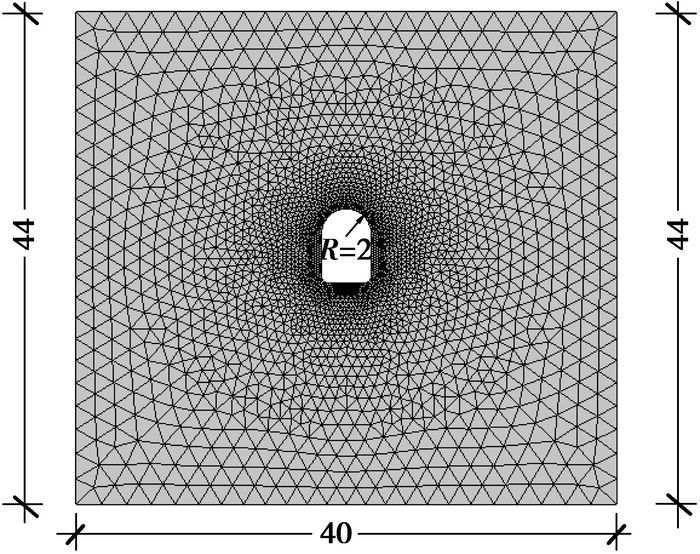
2.3 隧道模型隧道模型如图 8所示,隧道埋深16 m,洞高6 m。围岩为服从Mohr-Coulomb屈服准则与非关联流动法则(膨胀角ψ=0)的理想弹塑性材料,围岩的重度γ=20 kN/m3,粘聚力c=120 kPa,内摩擦角φ=23°,弹性模量E=1.5 GPa,泊松比υ=0.42,该隧道为一未支护的裸洞。为了避免局部应力集中造成计算不收敛,影响计算结果,在建模时,将拱墙与底板相交处的尖角采用圆弧过度。
|
图 8 算例隧道有限元计算模型(单位:m) |
按照式(6)对材料的强度进行折减,分别计算不同抗拉强度时隧道结构的安全系数并与“抗剪强度折减法”计算的结果对比,计算结果如表 3所示。可以看出,不同的抗拉强度指标对应的安全系数有较大的差别,说明抗拉强度T对隧道结构的安全性有较大的影响。
| 表 3 算例隧道安全系数 |
对于理想的弹塑性材料,材料一旦进入塑性状态,在应力不变的情况下应变可以无限增加,此时材料不能提供更多的强度来维护结构的稳定。
以T=18 kPa时隧道的破坏情况来说明受拉对维护隧道稳定性的作用,提取极限状态时(F=2.15)塑性区云图和受拉区的云图,如图 9、图 10所示。

|
图 9 算例隧道塑性区云图 |

|
图 10 算例隧道受拉区云图 |
可以发现:拱顶、底板、侧墙下部均产生了张性破坏。这些部位塑性区的产生显然与抗拉强度不足有一定的关系。侧墙上部虽然出现了受拉区但并未产生塑性区,说明这些部位虽然受拉但并非最薄弱的部位。对于不同的T值情况也是类似的,限于篇幅,不再一一展示。
隧道结构中大部分位置受压,但也会出现拉应力区,岩(土)材料的抗拉强度、抗剪强度都应是影响隧道安全性的重要因素。因此单一的采用抗剪强度指标折减或单一的采用抗拉强度指标折减均不能准确地描述隧道结构的安全储备大小,而采用“抗拉剪强度折减法”计算得到的结果应为比较正确的结果。
文中对隧道安全系数的计算也只是一个初步探讨。隧道的安全系数不仅仅受强度指标c,tan φ,T的影响,还可能与材料的变形参数有一定的关系。
文献[11]采用“抗剪强度折减法”对隧道的安全系数进行过一些讨论,得到“泊松比υ的取值对塑性区范围影响很大,但对安全系数基本上没有影响”这一结论。笔者认为此结论有可商榷之处。
假定某种土充满了半无限空间,其中的应力场仅由重力产生,深度h的一点的应力大小为
| $ {\sigma _1} = {\sigma _Z} = \gamma h, $ | (7) |
| $ {\sigma _2} = {\sigma _3} = {\sigma _X} = {\sigma _y} = \frac{\upsilon }{{1 - \upsilon }}\gamma h, $ | (8) |
式中:σz竖直方向的应力;σx,σy均为水平方向(x,y方向)的应力。对于同一个埋深的隧道,当竖直方向的荷载一定时,不同的泊松比对应于不同的侧向压力,隧道的安全系数显然会有较大差别。因此,泊松比对于隧道的稳定性应有较大的影响。
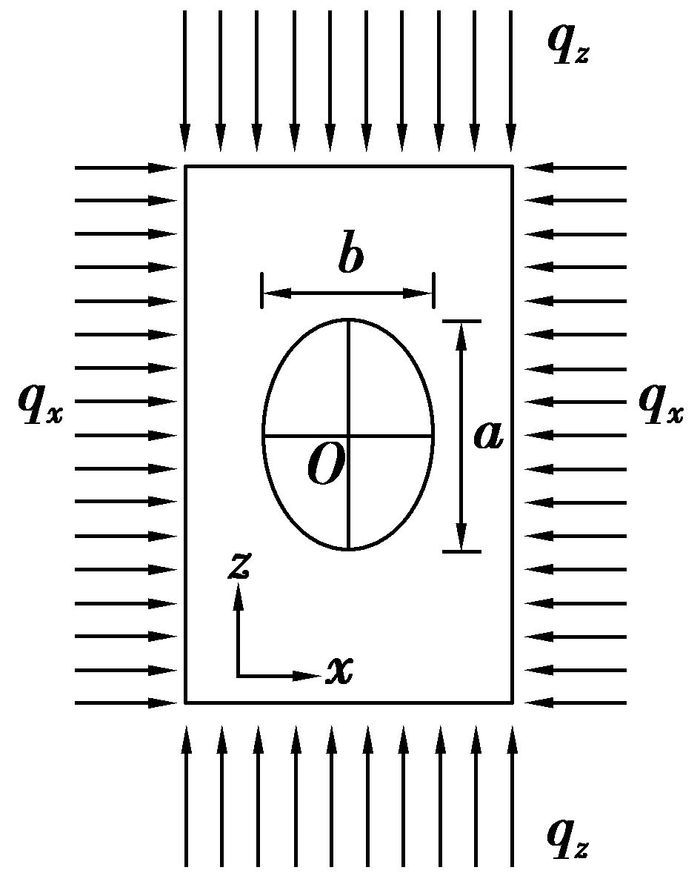
由弹性力学知识可知,如图 11所示的隧道时,隧道不出现拉应力,为最合理的轴比。
|
图 11 椭圆形洞室受力图 |
| $ \frac{a}{b} = \frac{{{q_Z}}}{{{q_X}}} = \frac{{\left( {1 - \upsilon } \right)}}{\upsilon }, $ | (9) |
岩土为满足Mohr-Coulomb屈服准则的理想弹塑性材料,因此σ1、σ3满足下式:
| $ \left( {1 - \sin \varphi } \right){\sigma _1} - \left( {1 + \sin \varphi } \right){\sigma _3} \le 2c \cdot \cos \varphi 。$ | (10) |
对于深部土体,取h→+∞时,将式(7)、(8)带入(10),解得
| $ \sin \varphi \ge 1 - 2\upsilon 。$ | (11) |
深埋的土体,即使受到边界的约束,由于强度折减也会使这部分土体发生剪切破坏。在边坡安全系数计算时,为了避免这种影响郑宏等[15]建议考虑泊松比的折减,使式(11)成立。
文中的研究主要说明抗拉强度对隧道安全系数的影响,变形参数对隧道安全系数的影响将在后续的研究中继续讨论。希望通过对多种影响隧道安全系数因素的讨论,建立起适用于隧道安全系数计算的强度方法。
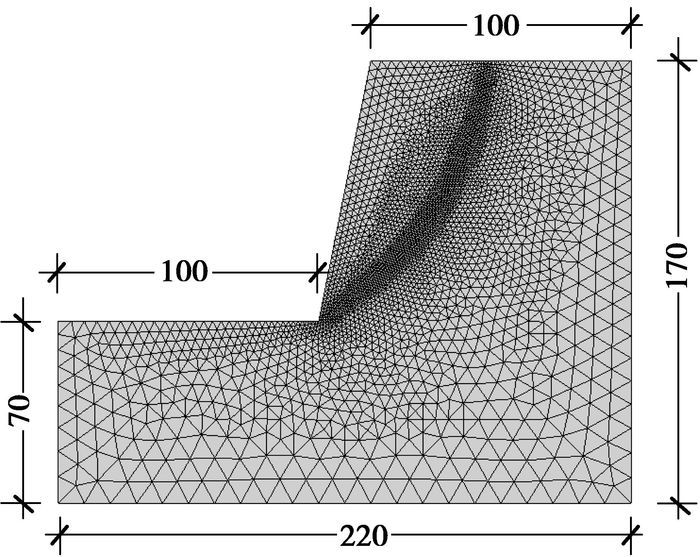
2.4 陡边坡模型陡边坡后缘往往会产生拉裂裂缝,选取有代表性的算例模型,如图 12所示,坡体为1:0.2的陡坡。坡体材料为服从Mohr-Coulomb屈服准则与非关联流动法则(膨胀角ψ=0)的理想弹塑性材料,材料的容重γ=22 kN/m3,粘聚力c=400 kPa,内摩擦角φ= 23°弹性模量E=10 GPa,泊松比υ=0.35。
|
图 12 陡边坡有限元计算模型(单位:m) |
用有限元强度折减法计算了“抗剪强度折减法”和“抗拉剪强度折减法”抗拉强度为不同取值时的安全系数,并与传统方法进行对比,计算结果如表 4所示。可以发现,在抗剪强度指标c、tanφ相同的前提下,不同的抗拉强度对应的安全系数有较大的差别。当认为抗拉强度为0时,计算得到的安全系数与抗剪强度折减法计算得到的安全系数误差超过10%以上,这将会对工程安全造成严重影响。按“抗剪强度折减法”计算的安全系数值大小与传统的方法计算得到的结果基本一致。传统的极限平衡法计算边坡的安全系数时,也没有考虑抗拉强度指标的影响。
| 表 4 陡边坡安全系数 |
提取T=60 kPa极限状态时(F=1.20)塑性区和受拉区的云图,如图 13、图 14所示。

|
图 13 陡边坡受拉区云图 |

|
图 14 陡边坡塑性区云图 |
从图 13中可以发现,边坡后缘很大一部分处于受拉的应力状态,将产生直线形的张性破裂面;边坡前缘为受剪破坏,为圆弧形的剪切破裂面。这一结果与滑坡实际的破坏形式比较一致。陡边坡中抗拉强度对边坡的稳定也起到了比较重要的作用。因此,采用“抗拉剪强度折减法”计算得到陡边坡安全系数更正确。
3 结论1) 分析了以往强度折减法存在的问题,即在强度折减过程中过高的考虑了岩土材料的抗拉性能使计算的安全系数值偏大。针对岩土材料张拉、剪切破坏的特征提出了“抗拉剪强度折减法”。这种方法既符合岩(土)材料张拉破坏的根本特征,又符合用“强度折减”求解安全储备的基本理念,在隧道工程、边坡工程中相对于原来的强度折减法更有适用性。
2) 对于受剪破坏为主的岩土结构(一般边坡),采用以往的“抗剪强度折减法”计算得到的安全系数是正确的;对于受拉破坏为主的岩土结构(钟乳石模型),须考虑抗拉强度的折减才能计算得到正确的安全系数;对于张拉、剪切破坏并存的的岩土结构(隧道及陡边坡),强度折减过程中采用“抗拉剪强度折减法”计算得到的结果应比较正确。
3) 目前隧道设计没有有效的定量计算方法,地层结构法计算的结果偏激进,会造成工程安全隐患;荷载结构法计算的结果偏安全,造成支护材料的浪费。目前隧道设计往往依靠工程类比来确定支护参数。采用以往的强度折减法计算隧道安全系数存在很多问题。通过文中计算表明:抗拉强度指标对隧道安全性影响很大,在强度折减过程中应予以考虑。此外,材料的变形参数可能对隧道安全系数也有一定的影响,笔者将在这方面深入研究,力图建立适用于隧道安全系数计算的强度折减法。隧道安全系数的计算可为隧道的概率设计奠定基础,最终可达到改进目前隧道的设计方法的目的。
| [1] | Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Géotechnique, 1975, 25(4): 671–689. DOI:10.1680/geot.1975.25.4.671 |
| [2] |
宋二祥.
土工结构安全系数的有限元计算[J]. 岩土工程学报, 1997, 19(2): 1–7.
SONG Erxiang. Finite element analysis of safety factor for soil structures[J]. Chinese Journal of Geotechnical Engineering, 1997, 19(2): 1–7. (in Chinese) |
| [3] |
赵尚毅, 郑颖人, 时卫民, 等.
用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报, 2002, 24(3): 343–346.
ZHAO Shangyi, ZHENG Yingren, SHI Weimin, et al. Analysis on safety factor of slope by strength reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343–346. (in Chinese) |
| [4] |
赵尚毅, 郑颖人, 邓卫东.
用有限元强度折减法进行节理岩质边坡稳定性分析[J]. 岩石力学与工程学报, 2003, 22(2): 254–260.
ZHAO Shangyi, ZHENG Yingren, DENG Weidong. Stability analysis on jointed rock slope by strength reduction FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2): 254–260. (in Chinese) |
| [5] |
郑颖人, 赵尚毅.
有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381–3388.
ZHENG Yingren, ZHAO Shangyi. Application of strength reduction FEM in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381–3388. DOI:10.3321/j.issn:1000-6915.2004.19.029 (in Chinese) |
| [6] |
郑颖人, 赵尚毅.
岩土工程极限分析有限元法及其应用[J]. 土木工程学报, 2005, 38(1): 91–104.
ZHENG Yingren, ZHAO Shangyi. Limit state finite element method for geotechnical engineering analysis and its applications[J]. China Civil Engineering Journal, 2005, 38(1): 91–104. (in Chinese) |
| [7] |
郑颖人, 赵尚毅, 孔位学, 等.
极限分析有限元法讲座:Ⅰ岩土工程极限分析有限元法[J]. 岩土力学, 2005, 26(1): 163–168.
ZHENG Yingren, ZHAO Shangyi, KONG Weixue, et al. Geotechnical engineering limit analysis using finite element method[J]. Rock and Soil Mechanics, 2005, 26(1): 163–168. (in Chinese) |
| [8] |
栾茂田, 武亚军, 年廷凯.
强度折减有限元法中边坡失稳的塑性区判据及其应用[J]. 防灾减灾工程学报, 2003, 23(3): 1–8.
LUAN Maotian, WU Yanjun, NIAN Tingkai. A criterion for evaluating slope stability based on development of plastic zone by shear strength reduction FEM[J]. Journal of Disaster Prevention and Mitigation Engineering, 2003, 23(3): 1–8. (in Chinese) |
| [9] |
陈力华, 张蕾.
有限元极限分析法的进展及在隧道工程中的应用探讨[J]. 公路交通技术, 2010(5): 84–88.
CHEN Lihua, ZHANG Lei. Development of finite element limit analysis methods and investigation on its application in tunnel projects[J]. Technology of Highway and Transport, 2010(5): 84–88. (in Chinese) |
| [10] |
戴自航, 刘志伟, 刘成禹, 等.
考虑张拉与剪切破坏的土坡稳定数值分析[J]. 岩石力学与工程学报, 2008, 27(2): 375–382.
DAI Zihang, LIU Zhiwei, LIU Chengyu, et al. Numerical analysis of soil slope stability considering tension and shear failures[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 375–382. (in Chinese) |
| [11] |
张黎明, 郑颖人, 王在泉, 等.
有限元强度折减法在公路隧道中的应用探讨[J]. 岩土力学, 2007, 28(1): 97–101.
ZHANG Liming, ZHENG Yingren, WANG Zaiquan, et al. Application of strength reduction finite element method to road tunnels[J]. Rock and Soil Mechanics, 2007, 28(1): 97–101. (in Chinese) |
| [12] |
曾亚武, 赵震英, 朱以文.
岩石材料破坏形式的分叉分析[J]. 岩石力学与工程学报, 2007, 21(7): 948–952.
ZENG Yawu, ZHAO Zhenying, ZHU Yiwen. Bifurcation analysis on failure forms of rock material[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 21(7): 948–952. (in Chinese) |
| [13] |
王来贵, 赵娜, 周永发, 等.
岩石受拉破坏的数值模拟方法[J]. 辽宁工程技术大学学报, 2007, 26(2): 198–200.
WANG Laigui, ZHAO Na, ZHOU Yongfa, et al. Numerical simulation method of rock bearing tension damage[J]. Journal of Liaoning Technical University, 2007, 26(2): 198–200. (in Chinese) |
| [14] |
俞茂宏, 刘继明, YoshiyaO D A, 等.
论岩土材料屈服准则的基本特性和创新[J]. 岩石力学与工程学报, 2007, 26(9): 1745–1757.
YU Maohong, LIU Jiming, Yoshiya O D A, et al. On basic characteristics and innovation of yield criteria for geomaterials[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(9): 1745–1757. (in Chinese) |
| [15] |
郑宏, 李春光, 李焯芬, 等.
求解安全系数的有限元法[J]. 岩土工程学报, 2002, 24(5): 626–628.
ZHENG Hong, LI Chunguang, LI Chaofen, et al. Finite element method for solving the factor of safety[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(5): 626–628. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

