2. 东南大学 土木工程学院, 南京 210096;
3. 中南大学 土木工程学院, 长沙 410075
2. College of Civil Engineering, Southeast University, Nanjing 210096, China;
3. School of Civil Engineering, Central South University, Changsha 410075, China
大跨空间钢结构的施工过程是结构由基本构件到部分结构,再到整体结构逐步集成的动态变化过程[1],在此过程中,结构的外形、拓扑、刚度、边界条件、荷载状况等都在不断发生变化,从而引起结构体系不断发生转换,而且不同的施工方法和施工顺序会引起不同的结构成形态构形和最终的受力状态[2]。因此,传统的只关心最终成形状态的结构设计方法已不能满足要求,对于大跨空间钢结构,不仅要重视结构的最终设计状态,也应关心结构的施工成形过程。为确保整个施工过程中结构的安全性,以及施工完成后整体结构的可靠性,必须对结构进行施工全过程的力学分析[3]。
大跨度弦支穹顶作为一种结合了张力结构和网壳结构优点的新型空间钢结构,近年来在城市公共建筑的应用越来越多,不仅结构的跨度越来越大而且结构的几何外形也变得日益丰富。这些特征的变化对预应力施工技术提出了更高要求,同时结构跨度的增大、结构组成复杂,预应力施工过程中影响结构成形和受力的因素较多,因此对大跨度弦支穹顶进行预应力施工全过程及施工影响因素的力学分析越来越重要。
弦支穹顶的施工包括了上部钢结构的安装和下部索杆系的安装及张拉,预应力施工过程可认为是结构由施工零状态逐步向施工初始态转变的过程,随着北京工业大学体育馆、武汉体育中心体育馆、常州体育会展中心体育馆以及济南奥体中心体育馆等大跨度弦支穹顶的相继建成,国内外学者一直致力于弦支穹顶结构预应力施工全过程的力学分析[4-9],对影响预应力拉索施工的多因素进行了多方面分析研究,以期准确把握预应力施工各阶段的结构状态。
1 弦支穹顶预应力施工特点近年来,由于弦支穹顶结构跨度的不断增大(多项工程突破了百米跨径),使得其下部索杆体系的数量增多、索径增大,且拉索的设计索力也越来越大。预应力施工时,考虑到张拉设备和人员等条件的限制,预应力施工单位一般不可能对结构中所有需要张拉的拉索同时同步张拉至设计索力,而是采用分批次张拉的预应力施工工艺。故弦支穹顶结构的施工流程一般可划分为3大步骤:
第1步:在支撑架上安装刚构和索杆系;
第2步:分批次张拉预应力拉索;
第3步:主动脱架或被动脱架,结构成形达到施工初始态。
在预应力施工过程中,弦支穹顶的结构构件与支撑系统构成了一个施工临时结构[6]。该临时结构随着施工过程发生着非线性的变化,主要表现为以下方面。
1.1 存在结构体系的转换1) 上部钢网壳和拉索安装时,钢网壳和拉索自重由支撑系统承担,支撑系统构成了该阶段的施工临时结构。
2) 上部钢网壳和拉索安装完毕,拉索分批次张拉时,上部钢网壳、已张拉拉索以及支撑系统构成了该阶段的施工临时结构。
3) 拉索张拉完毕,并主动或被动脱架后,弦支穹顶的结构构件与支撑系统分离,施工临时结构转化为永久的设计结构,达到弦支穹顶结构的施工初始态。
1.2 存在非线性接触支撑与上部钢网壳的接触状态是随张拉过程变化的:当支撑承压时,其与上部钢网壳之间为接触状态;当支撑与上部网壳脱开时,则为非接触状态。
1.3 存在几何非线性预应力施工过程中,结构尚未完全成形之前,此时由上部钢网壳、已张拉拉索以及支承系统构成的施工临时结构刚度较小,继续张拉下一批拉索时,施工临时性结构可能会产生较大的变形,即存在较大的几何非线性。
1.4 索力之间的相互影响由于大跨度弦支穹顶的索杆体系较多,预应力张拉需分批次进行,若张拉过程中的临时结构刚度较小,后续张拉的拉索易引起临时结构的变形,导致已张拉完成的拉索索力发生变化。即某根拉索按照设计索力张拉到位,则待后续其它拉索张拉后,该索的索力又发生变化,从而偏离设计索力。
总之,由于施工结构体系转换、非线性接触、几何非线性和索力间相互影响等原因,使得弦支穹顶的预应力施工全过程变得非常复杂。因此,为准确获取施工各阶段的控制参数,应在预应力施工方案确定时,考虑施工多因素非线性耦合的影响,进行预应力施工的全过程模拟分析。
2 弦支穹顶预应力施工过程分析方法如前所述,国内外学者对弦支穹顶的预应力施工过程分析方法进行了较全面的研究,现阶段应用较多的分析方法主要有:状态变量叠加法、反分析法和生死单元法。
2.1 状态变量叠加法状态变量叠加法,以凝固的时间点将连续的施工过程划分为若干施工时间段,假定在每个时间段内施工临时结构及其荷载是不变的,对各时间段的施工临时结构进行求解,获得各时间段的施工临时结构状态(如内力、变形等)的变化量,最终结构状态为各时间段的施工临时结构状态(如内力、变形等)的变化量之和。
该方法简单,各时间段的分析顺序并不需要与施工过程一致,适用于支撑条件简单、刚度较大的线性结构。但将其应用于弦支穹顶预应力施工过程模拟时,其缺点也是明显的。
1) 对非线性接触难以模拟。若支撑系统的支撑点较多或支撑刚度变化较大,如满堂支撑系统,则计算非常繁杂,难以适用;
2) 状态变量叠加法最后将各时间段的状态变量简单的线性叠加,这对于存在具有较强几何非线性施工临时结构的施工过程,采用该方法计算所得的结果存在一定的局限性。
因此,状态变量叠加法对于支撑点较多或半刚性和柔性的弦支穹顶预应力施工过程模拟并不适用。
2.2 反分析法文献[7]采用反分析方法对弦支穹顶的预应力施工过程进行了分析。以设计初始状态下的结构几何构形、拉索索力等作为分析的起点,按照与实际施工步骤相反的顺序对拉索进行放松,即通过倒拆手段来反向跟踪施工过程,并计算各施工阶段的拉索索力和结构变形,直到所有预应力拉索全部放松。对于弦支穹顶结构而言,由于反分析法直接从已知的设计初始态开始,逆向分析各批次张拉的未知状态,并获得各张拉施工阶段的张拉力等,计算相对较为简便。
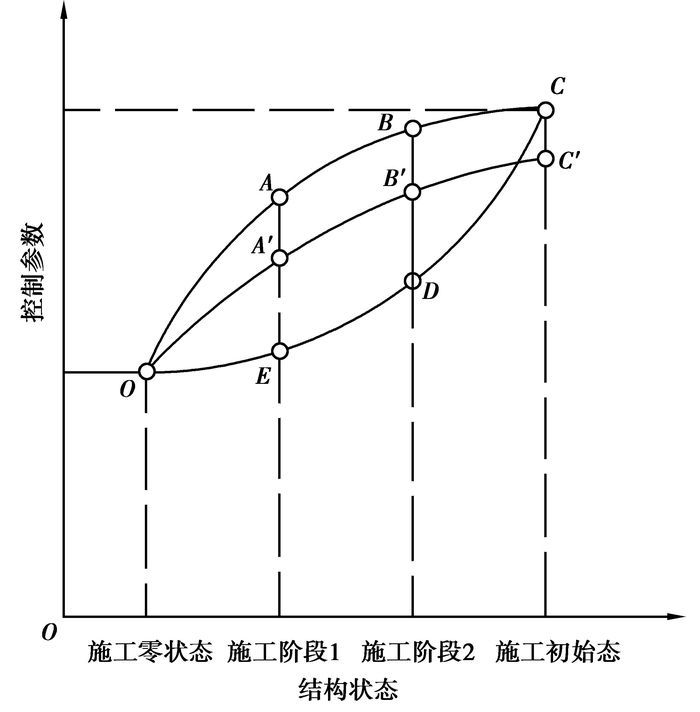
需要特别说明的是,弦支穹顶施工全过程反分析法适用的关键是正向施工与反向分析的结构状态路径在各个施工阶段必须完全一致,而不能仅仅是施工零状态与施工初始态一致,如图 1所示:OABC表示整个预应力施工过程的顺序施工路径,而CDEO为反向分析路径,采取施工反分析法确定施工阶段1和施工阶段2的张拉控制参数E和D,但由于顺序施工和反向分析路径的不重合,而实际施工时需要的控制参数为A和B,导致按照反分析法所得控制参数E和D进行顺序施工时,结构的预应力施工路径变为OA′B′C′,最终导致施工初始态的控制参数(C和C′)差别较大,难以满足设计要求。因此,反分析法用于预应力施工过程分析时,整个施工过程应具有保守性,即顺序施工和反分析的路径完全重合,而对于非保守的预应力施工过程,反分析法则不适用。
|
图 1 弦支穹顶预应力施工路径图 |
文献[9]采用了有限单元法当中的生死单元法模拟预应力拉索施工过程,即根据预应力的施工过程选择“杀死”和“激活”的单元,并在各施工阶段赋予“激活”单元相应的拉索张拉力。
采用生死单元法进行预应力拉索施工全过程模拟时,未张拉部分的单元处于“杀死”状态,而这种“杀死”的单元并真实的从结构中移除,其与“激活”单元仍通过节点连接,有限元分析软件常用的处理方法是将“杀死”单元的刚度矩阵乘以一个极小数值(常取为10-6),从而使其刚度不会影响“激活”单元且自身应变也不会改变。
但是,当结构施工阶段非线性较强时,“激活”单元位移变化较大会带动“杀死”单元产生较大的伸长或缩短,导致“杀死”单元被“激活”后单元长度与初始长度差别较大,最终导致施工过程模拟的失败。
3 基于等效预张力的预应力施工过程正算法预应力施工过程正算法是指整个预应力施工分析过程与实际张拉过程是完全一致的,即分析路径和施工路径是重合的。显然,与施工过程同顺序进行分析,符合工程实际,无需关注过程保守性的问题,且分析中的非线性问题能通过采用非线性有限元分析方法得到很好地解决。但需要明确的是,预应力施工的目的就是实现设计给定的预应力态,而在实际施工准备阶段,往往已知的是设计给定的设计初始态即施工过程分析的终点,而分析的起点——施工零状态却是未知的,因此当正算法应用于弦支穹顶预应力施工过程分析时,需根据设计初始态确定施工零状态和各张拉阶段拉索张拉力,然后才能进行预应力施工全过程分析。
3.1 拉索等效预张力首先,对索力和拉索等效预张力进行概念上的解释,预应力施工过程正算法即按照拟定的张拉方案进行结构分析,当计算至对某根(批)拉索进行张拉时,需要该索的施工张拉力,而前面已叙述,由于索力相互影响以及结构非线性等原因,为保证施工初始态下达到目标索力,施工张拉力并不一定等于目标索力,而是未知的、待求的参数。
索力是拉索等效预张力和其它荷载作用下结构达到平衡态时的拉索内力,其变化是相当“活跃”的,在施工过程和使用过程中不断变化。而拉索等效预张力则是以等效初应变或等效温差的形式施加在拉索上,模拟拉索张拉的媒介手段。当结构张拉成形后,拉索中的等效预张力并不会随荷载(包括结构自重、环境温度等)和结构形状的变化而变化。同样,施工过程中当某根索或某环索张拉完成后,在其再次张拉之前,该索内的等效预张力是不变的。可见,等效预张力具有在施工过程中相对稳定和在使用过程中恒定的特点,即拉索等效预张力只有对该索再次张拉才会改变。
张拉过程中对某根(批)索张拉的施工张拉力,可理解为:此时的施工临时结构在该根(批)索和已张拉索的等效预张力以及该施工临时结构的自重作用下达到平衡态时的索力。因此,正算法所需的施工张拉力,可转为需要的等效预张力。当拉索分批次张拉,则在张拉方案中应明确每次所有拉索张拉完毕后的索力值。这里需要明确的是,与设计初始态找力分析不同的是,张拉过程找力分析应建立符合实际施工状况的施工临时结构整体模型,包含支撑系统和预应力钢结构等,并以设计给定的预应力态为目标,确定各张拉阶段的等效预张力。
当各次张拉的等效预张力确定后,即可采用正算法进行张拉过程分析。当计算至第i次对第j根索张拉时,只要在临时施工结构中将该索的第i次张拉的等效预张力施加在该索上,求解后得到的索力也就是该索第i次张拉的施工张拉力。值得注意的是:当第i次张拉时拉索张拉顺序发生变化,该次张拉的等效预张力是不变的,而施工张拉力是变化的,可见等效预张力具有良好的“稳定性”。
3.2 正算法的分析方法和具体步骤假定某弦支穹顶结构中共有K根拉索,已知设计初始态的基准温度Ts、结构位形以及拉索索力F。施工方案为:上部钢网壳和索杆系在支撑体系上安装,安装完毕后在支撑上开始张拉;将拉索分为M批,分N次张拉完成,且明确每次所有索张拉后的索力值;为避免支撑对最终成形态的影响,在N-1次张拉结束后,主动脱架,然后在无支撑情况下最后一次张拉。
为考虑结构非线性,分析中均可采用非线性有限元求解。基于等效预张力的正算法张拉过程分析的方法和具体步骤,如下:
步骤1:采用迭代算法,计算设计基准温度Ts下的施工初始态及其施工等效预张力Pc。
步骤2:由于预应力施工后的施工初始态要与设计初始态的结构位形基本相符,因此可根据需要进行全结构零状态找形或索杆系子结构零状态找形,确定施工零状态下的结构位形。
步骤3:以施工零状态结构位形建立包含支撑体系的施工临时结构模型。模型中各个构件的单元类型:支撑可采用仅受压、不受拉的非线性杆单元,模拟支撑与刚构的非线性接触;拉索可采用仅受拉、不受压、不受弯的索单元;其它构件根据受力特点可选用梁单元或杆单元等。考虑到一般施工中,在支撑顶部设千斤顶或可调托等装置,以调整安装标高,因此模拟支撑的仅受压非线性杆单元可设定为大刚度和无自重。但需要设定材料温度膨胀系数,以便于模拟结果的主动落架。
步骤4:在施工临时结构模型上,以各次张拉完毕的目标索力,进行拉索等效预张力的找力分析,确定各次张拉的施工等效预张力Pci(第i次张拉的施工等效预张力),其中最后一次的施工等效预张力PcN即为步骤1确定的Pc。等效预张力的确定方法有增量法、比值法、补偿法、混合法等。
步骤5:按照既定方案中的张拉顺序,依次进行第i(i=1,2,…,N-1)次张拉过程分析。当对第j根(批)拉索张拉分析时:
1) 对于尚未进行张拉的拉索,可施加较大的负等效预张力(即等效预压力),使拉索松弛,不参与整体结构工作;
2) 对于i次张拉的拉索,则施加该次张拉的等效预张力Pcij;
3) 对于i次不张拉,但i-1次已张拉的拉索,则施加上次张拉的等效预张力Pc(i-1)j;
4) 求解得到施工临时结构的平衡态,获取第j根(批)拉索张拉后的结构响应,如:结构变形、构件应力以及已张拉索的索力等。其中第j根(批)拉索的索力,即为第i次张拉的第j根(批)拉索的施工张拉力。
步骤6:进行完第N-1次所有拉索的张拉分析后,按照拟定的施工方案需要进行整体结构的主动脱架。此时,仅要在所有拉索上施加第N-1次的施工等效预张力,然后再在支撑上施加较大的正初应变或较大的负温差,使支撑回缩以模拟主动脱架,最后求解得到主动脱架后的结构状态。
步骤7:第N次张拉过程分析。按照第N次张拉顺序,依次施加等N次张拉的施工等效预张力,即可获得第N次第j根(批)拉索张拉后的结构状态以及相应的施工张拉力。
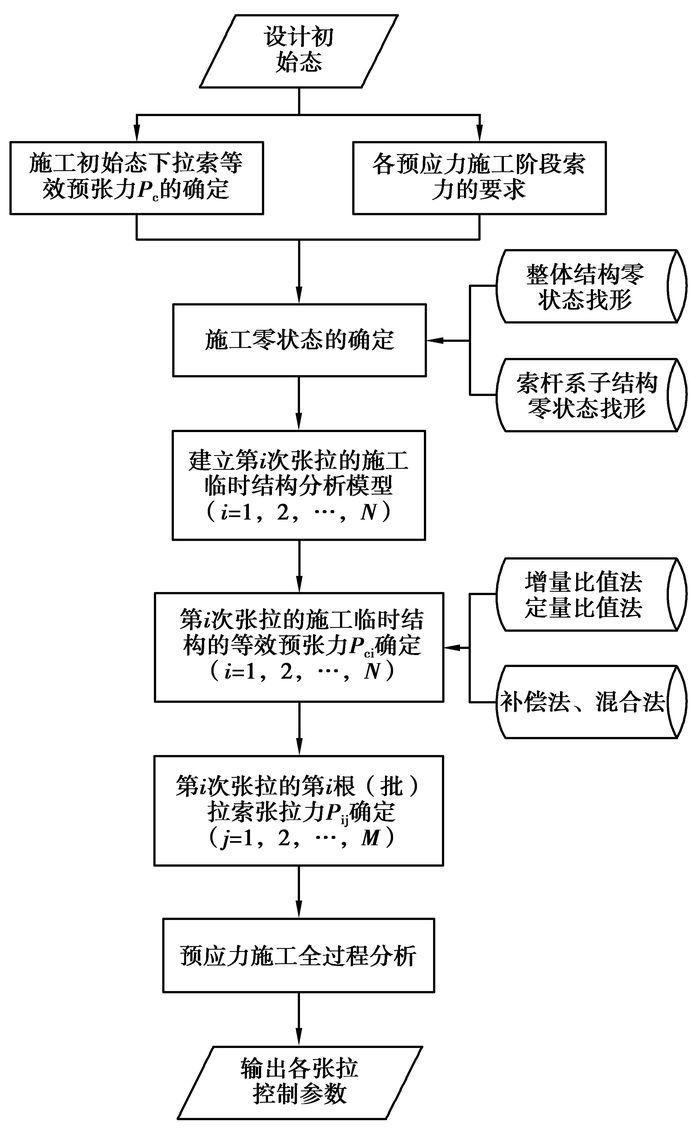
根据上述方法和步骤,可编制基于等效预张力的正算法计算流程,如图 2所示。
|
图 2 基于等效预张力的预应力施工过程正算法 |
以常州体育会展中心体育馆弦支穹顶钢屋盖弦支穹顶结构实际工程为算例,在索杆系子结构施工零状态的找形分析、等效预张力的确定以及施工张拉方案拟定的基础上,对其预应力施工全过程进行分析。
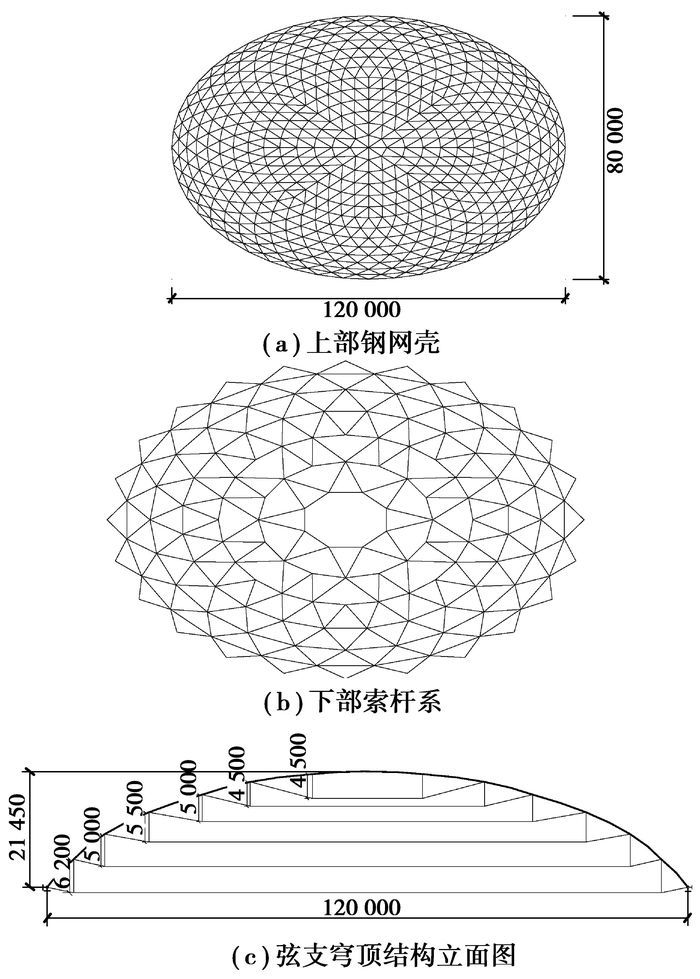
该弦支穹顶结构的形状为椭球形,平面投影的椭圆长轴为120 m,短轴80 m,屋盖矢高21.45 m,长轴矢跨比为0.179,短轴矢跨比为0.268,属于高矢跨比椭球形弦支穹顶。结构上部钢网壳为单层网壳,沿径向划分为14环(环编号由内到外),由中心至第6环的网格形式为Kiewitt型(K8)、第6环至第14环的网格形式为Levy型。预应力索系布置形式为Levy型,由环索、径向索和撑杆构成,共设6环,如图 3所示。
|
图 3 常州体育馆钢屋盖计算模型简图 |
网壳结构的杆件均采用圆钢管,材质为Q345,弹性模量取为2.06×105 N/mm2。其中,Kiewitt型网格形式的杆件截面均为Φ273×10,第7环至第11环的环向杆件和径向杆件截面均为Φ273×8,第12环和第13环的环向杆件以及第12环的径向杆件截面均为Φ273×12,其余杆件截面为Φ273×16。该弦支穹顶结构共有24个支座节点,除支座节点采用焊接球节点外,其余所有节点均采用铸钢节点,铸钢件材质为GS-20Mn5V。索夹采用铸钢节点形式,铸钢件材质为GS-20Mn5V。撑杆采用圆钢管,材质为Q345,弹性模量取为2.06×105 N/mm2,杆件截面为Φ180×10,撑杆上端采用万向球铰与网壳节点铰接,撑杆下端与铸钢索夹节点固接。支座均为三向不动铰支座。
预应力拉索采用1670级Φ5镀锌钢丝双护层扭绞型半平行钢丝拉索,预应力施工过程模拟分析时,拉索材料的弹性模量取为1.95×105 N/mm2。各环预应力拉索的规格见表 1,环索编号由内到外为HS-1~HS-6、径向索编号由内到外为JXS-1~JXS-6。
| 表 1 常州体育馆预应力拉索材料表 |
该弦支穹顶结构基于等效预张力的正算法应用的具体步骤为:
1) 建立完整的施工分析模型:由于该结构在正式张拉前已主动落架,故分析模型中仅包含整个屋盖系统,而不含支承系统,分析模型相对简单;
2) 环索张拉索段的找力分析:分别确定索力达到预紧力和100%设计索力时环索张拉索段的等效预张力Pc0和Pc1,其中,预紧力外四环取为设计初始态下索力的5%,内两环取为10%,并根据实际情况适当调整预紧力;
3) 已张拉环索索段等效预张力的施加:根据预应力施工流程由外到内逐环施加第i次张拉时已张拉环索索段的等效预张力Pci,未张拉的环索索段等效预张力仍赋值为Pc0;
4) 按照张拉过程连续求解:获得各张拉阶段的结构状态以及各次、各批环索张拉索段的施工张拉力。
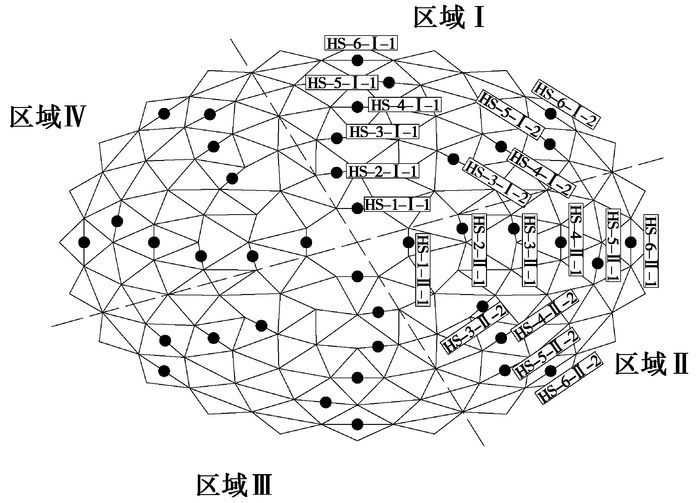
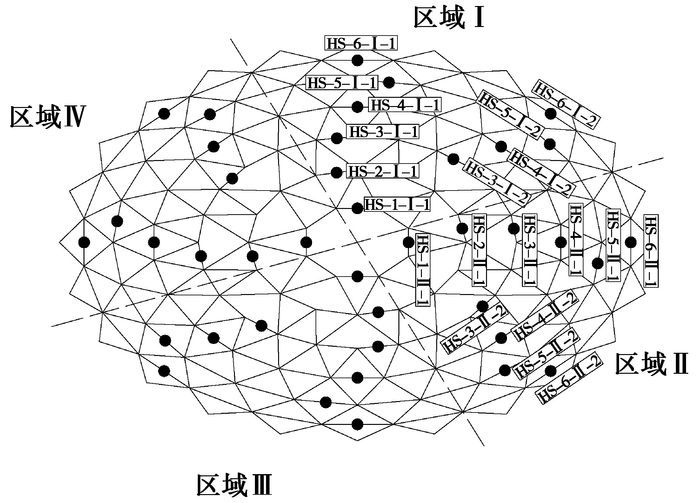
4.1 等效预张力的确定根据上述计算,环索索夹设定可滑动节点,分别确定预应力拉索初紧状态和设计初始态的等效预张力,张拉过程中的张拉分区和张拉点布置见图 3所示,其中区域Ⅰ和区域Ⅲ、区域Ⅱ和区域Ⅳ的各张拉点对称,故仅对区域Ⅰ和区域Ⅱ的各张拉点进行编号。
4.1.1 拉索预紧状态根据设计初始态下各环环索的索力,确定各环张拉点的拉索预紧力,由外到内依次为50、36、30、25、20、10 kN,应用补偿法计算各张拉点处环索索段预紧时的等效预张力Pc0,其中补偿因子为10,收敛容差为5%,预紧状态下各张拉点的等效预张力如表 2所示。
| 表 2 拉索预紧状态的拉索索力和等效预张力 |
根据环索索夹为可滑动节点这一构造,调整原设计给定的设计初始态下各环拉索索力,得出各张拉点的设计索力有外到内依次为1 050、720、610、400、200、90 kN。依据设计初始态下各张拉点的设计索力,应用补偿法进行各张拉点等效预张力Pc的确定,其中补偿因子取为5,收敛容差设为5%,设计初始态下各张拉点的等效预张力见表 3。
| 表 3 设计初始态下的设计索力和等效预张力 |
根据预紧状态和设计初始态下的等效预张力以及拟定的拉索整体张拉施工方案[10],进行该弦支穹顶结构的预应力施工全过程分析。
确定各张拉施工阶段张拉索段的张拉力是预应力施工全过程分析的主要目的之一,因此,根据拟定的施工方案进行预应力施工全过程分析之后,需提取各施工阶段张拉点处的环索索力(见表 4),并对各环索力之间的相互影响进行分析(见图 4),其中预应力施工分析步骤为:预紧(YJ)→HS-6张拉至100%张拉力(step-1)→HS-5张拉至100%张拉力(step-2)→HS-4张拉至100%张拉力(step-3)→HS-3张拉至100%张拉力(step-4)→HS-2张拉至100%张拉力(step-5)→HS-1张拉至100%张拉力(step-6)。
| 表 4 预应力拉索施工过程中各张拉点的环索索力 |
|
图 4 常州体育馆预应力拉索施工分区及张拉点布置 |
|
图 4 预应力拉索施工过程中各张拉点索力变化 |
1) 由表 4可得,各张拉阶段张拉点处的环索索力即张拉力与设计初始态下不同。因此,根据设计初始态下给定的拉索索力,结合施工零状态找形分析、拉索等效预张力确定方法,采用基于等效预张力的正算法进行预应力施工全过程分析是必要的。
2) 由于常州体育馆上部钢网壳刚度较大,张拉过程中,环与环之间的拉索索力影响较小。预应力施工完成后,HS-6的环索索力增大约3.7%,HS-5的环索索力增大约4.6%,其余各环索力增量则均小于2%。因此,对该结构待拉索预紧后,采用先被动落架,然后依次由外到内张拉且一次张拉到位的施工方案是可行的。
5 结论1) 考虑到大跨度弦支穹顶施工过程中的多因素非线性耦合效应,进行弦支穹顶预应力施工全过程模拟分析时,结构模型、本构关系、临时支撑刚度、施工程序、施工顺序等均应与实际施工过程吻合,基于此获得的预应力施工各阶段的控制参数,才能够保证预应力施工完成后的结构状态满足设计初始态要求。
2) 正算法的应用建立在设计初始态已知和预应力施工初步方案拟定的基础上,通过大跨度弦支穹顶结构预应力施工零状态找形分析确定预应力施工的起点,根据找力分析确定各施工阶段索杆系中各单元的等效预张力(找力分析模型需考虑临时支撑系统等),进行预应力施工全过程的分析,获取不同张拉阶段各张拉点的张拉力及关键节点位移等控制参数。
3) 通过建立基于等效预张力的预应力施工过程正算法,可精确模拟预应力施工过程,基于虚拟张拉技术构建的分析模型能够便于技术人员对方案的可行性进行判断,优化或调整预应力施工方案等。
| [1] |
王光远.
论时变结构力学[J]. 土木工程学报, 2000, 33(6): 105–108.
WANG Guangyuan. On mechanics of time-varying structures[J]. China Civil Engineering Journal, 2000, 33(6): 105–108. (in Chinese) |
| [2] |
曹志远.
土木工程分析的施工力学与时变力学基础[J]. 土木工程学报, 2001, 34(3): 41–46.
CAO Zhiyuan. Construction mechanics and time-varying mechanics in civil engineering[J]. China Civil Engineering Journal, 2001, 34(3): 41–46. (in Chinese) |
| [3] |
刘学武, 郭彦林.
考虑几何非线性钢结构施工力学分析方法[J]. 西安建筑科技大学学报:自然科学版, 2008, 40(2): 161–169.
LIU Xuewu, GUO Yanlin. Construction mechanics analytical procedures for steel structures in view of the geometric nonlinearity[J]. Journal of Xi'an University of Architecture & Technology:Natural Science Edition, 2008, 40(2): 161–169. (in Chinese) |
| [4] |
李永梅, 张毅刚, 杨庆山.
索承网壳结构施工张拉索力的确定[J]. 建筑结构学报, 2004, 25(4): 76–81.
LI Yongmei, ZHANG Yigang, YANG Qingshan. Determination of cable forces during construction for cable supported lattice shells[J]. Journal of Building Structures, 2004, 25(4): 76–81. (in Chinese) |
| [5] | Kitipornchai S, Kang W J, Lam H F, et al. Factors affecting the design and construction of Lamella suspen-dome systems[J]. Journal of Constructional Steel Research, 2005, 61(6): 764–785. DOI:10.1016/j.jcsr.2004.12.007 |
| [6] |
张爱林, 李鹏飞, 刘学春.
考虑临时支撑的弦支穹顶结构施工仿真分析[J]. 工业建筑, 2009, 39(1): 105–109.
ZHANG Ailin, LI Pengfei, LIU Xuechun. Construction emulation analysis of suspendome considering temporary supports[J]. Industrial Construction, 2009, 39(1): 105–109. (in Chinese) |
| [7] |
曲晓宁, 罗尧治, 娄荣.
控制索原长求解索张拉力的反分析法[J]. 哈尔滨工业大学学报, 2009, 41(10): 114–117.
QU Xiaoning, LUO Yaozhi, LOU Rong. Inverse analysis method for calculating cable tension based on controlling the initial length of cables[J]. Journal of Harbin Institute of Technology, 2009, 41(10): 114–117. DOI:10.3321/j.issn:0367-6234.2009.10.023 (in Chinese) |
| [8] |
郭佳民, 袁行飞, 董石麟, 等.
弦支穹顶施工张拉全过程分析[J]. 工程力学, 2009, 26(1): 198–203.
GUO Jiamin, YUAN Xingfei, DONG Shilin, et al. Global-process pretensioning analysis of suspend-dome[J]. Engineering Mechanics, 2009, 26(1): 198–203. (in Chinese) |
| [9] |
张国军, 葛家琪, 秦杰, 等.
2008奥运会羽毛球馆弦支穹顶预应力张拉模拟施工过程分析研究[J]. 建筑结构学报, 2007, 28(6): 31–38.
ZHANG Guojun, GE Jiaqi, QIN Jie, et al. Simulating analysis of prestressing construction process of the suspend-dome of the badminton gymnasium for 2008 Olympic Games[J]. Journal of Building Structures, 2007, 28(6): 31–38. (in Chinese) |
| [10] |
王永泉, 郭正兴, 罗斌, 等.
常州体育馆大跨度椭球形弦支穹顶预应力拉索施工[J]. 施工技术, 2008, 37(3): 33–36.
WANG Yongquan, GUO Zhengxing, LUO Bin, et al. Prestressed cable construction of large-span elliptic suspended-dome in Changzhou gymnasium[J]. Construction Technology, 2008, 37(3): 33–36. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

