无线传感网络在环境监测、建筑安全、汽车电子、武器装备等军民领域具有广泛的应用。随着无线传感网络节点的微型化、多功能化和无人值守的发展需求,体积大、寿命短的传统电源已经成为了限制其发展的技术瓶颈,亟待解决。微型能量收集器能够不断地获取环境中的能量并转化为电能,具有体积小、寿命长、免维护和绿色环保等优点,已成为国际上研究的热点。目前在能量收集技术领域,大多数研究都关注于环境振动能[1-5]、太阳能[6]、热能[7]等形式的能量收集,对于风能收集技术的研究较少。微型风能收集器能为无线传感网络节点的电源问题提供新的解决方案。
典型的风能收集器是大型风力发电机,主要由扇叶、电磁发电机和转动机构组成,结构复杂,在微型化的过程中加工与安装都很困难[8]。而且轴承的摩擦力和材料疲劳在微尺度下更显著,其可靠性和工作效率低。相比之下,基于风致振动机理的微型风能收集器结构简单,更适合微小尺度下的加工与应用。
振动能到电能的转化方式主要有3种:压电、电磁和静电。其中压电式的能量转换结构最简单,且能量密度高,是微型能量收集器领域的重点[1-2]。目前对压电式微型风能收集器的研究中,主要应用锆钛酸铅(PZT)和聚偏氟乙烯(PVDF)2种压电功能材料。其中PZT材料具有优良的压电性能,但弹性刚度常数较大,风致振动的强度小,临界风速高。相比之下,PVDF具有更小的刚度常数,大约只有PZT的1/20,在低速风载荷下易发生大幅度的振动或摆动,但其压电性能相对较差,d31系数只有PZT的1/14。Pobering[9]基于涡激振动原理,将PZT压电梁放在45 m/s的风中,只得到了54 μW的输出功率。Akaydin[10]将柔性的PVDF压电膜片放在圆柱体后的涡街内,在6.8 m/s(Re=14 800)的风速下发生涡激振动,输出功率只有4 μW。为了提高微型风能收集器的输出性能,Kwon[11]采用T型的结构获取风能,将6个PZT压电片安装在结构应力最大的固定端,临界风速为4 m/s。在15 m/s的风速下,输出功率4 mW,但体积较大。Li Shuguang等人[12]在PVDF压电膜(柄)的自由端横向铰链一个三角形的膜片(叶),设计了L型的压电树叶,叶片在风中的颤振带动压电片振动,临界风速4 m/s,最大输出功率为0.6 mW。
为了降低PZT压电梁的临界风速,解决风致振动的问题,文中提出了一种柔性梁和PZT压电梁的复合结构,具有高性能、低临界风速、体积小等优点。加工了不同尺寸的原理样机,开展了气动特性和电学特性的风洞实验研究。
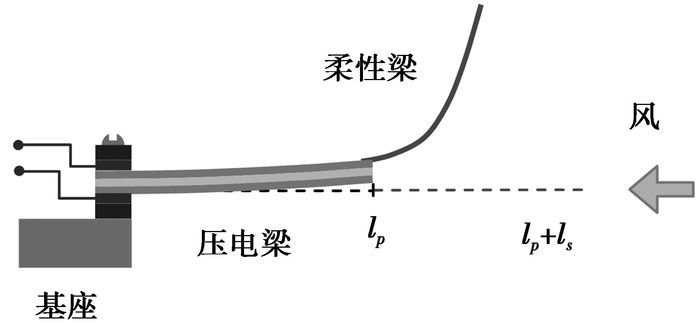
1 结构与原理 1.1 结构微型风能收集器结构如图 1所示,一个矩形的柔性梁安装在PZT压电悬臂梁的自由端,与旗帜结构类似,但风向相反,从柔性梁自由端吹向PZT梁固定端。由于柔性梁的刚度小,在低风速下就可触发颤振。柔性梁牵引PZT压电梁一起振动,可解决单一PZT压电悬臂梁临界风速高难以振动的问题。
|
图 1 压电式微型风致振动能量收集器原理图 |
风致振动能量收集器的原理主要分为柔性梁的颤振和PZT梁的压电效应2部分。作为典型的流固耦合现象,柔性梁在风中的颤振是由气动力、惯性力与弹性力的耦合的结果,其本质在于风与结构之间的能量的转化。在1个振动周期内柔性梁吸收的风能等于消耗的能量时就发生颤振。目前对于颤振的研究大多是针对临界风速的估算,对颤振后的动力学特性分析还不成熟[13]。根据Tang[14]和Eloy等[15]的分析,可给出微型风能收集器临界风速Ucr的经验公式:
| ${U_{cr}} = \frac{{{U_0}}}{{{l_{\rm{s}}}}}\sqrt {\frac{{EI}}{{(1 - {\nu ^2})\rho A}}} ,$ | (1) |
其中:U0是折合临界风速;EI、ν、ls、A、ρ分别为柔性梁的截面弯曲刚度、泊松比、长度、截面积和密度。
PZT梁的压电效应是微型风致振动能量收集器的机电耦合部分,由PZT材料的正压电效应将颤振引起的振动能转化为电能。根据伯努利欧拉梁原理,PZT压电梁的运动方程表示为[2]
| ${E_p}{I_p}\frac{{{\partial ^4}u}}{{\partial {x^4}}} + c\frac{{\partial u}}{{\partial t}} + {\rho _{\rm{p}}}{A_{\rm{p}}}\frac{{{\partial ^2}u}}{{\partial {t^2}}} = {f_{\rm{s}}},$ | (2) |
其中:u表示PZT梁的挠度;EpIp、ρp和Ap分别是PZT梁的截面弯曲刚度、密度和截面积;c是阻尼系数;fs表示柔性梁根部对PZT梁垂直方向的牵引力。
PZT梁的振动使得压电材料在悬臂梁长度方向产生交替的应变S1为:S1=-z∂2u/∂x2。z表示压电梁中压电材料到中性面的厚度。结合压电方程[1-3]得到PZT电极上的电位移矢量D3=d31EpS1。d31和Ep分别为PZT的压电常数和杨氏模量。在PZT的电极上产生的电荷为
| $Q = {w_{\rm{p}}}\smallint _0^{{l_p}}{D_3}{\rm{d}}x,$ | (3) |
其中,wp为PZT梁宽度。得到PZT梁上下电极上的电压为
| $V = \frac{Q}{C},$ | (4) |
其中,C为PZT上下电极间的电容。
2 实验测试 2.1 样机加工微型风能收集器采用0.1 mm厚的聚对苯二甲酸乙二醇酯(PET)膜作为柔性梁。PET膜分3组,宽度ws分别为6.4、8、10 mm,长度在15~30 mm范围内(见表 1)。PZT梁为3层结构的压电双晶片(Piezo Systems公司,T215-H4-203X),2层压电材料为PZT-5H,中间层为铜,每层厚度都是0.127 mm。PET膜的弯曲刚度为2.1×10-6~3.3×10-6 Nm2,而PZT梁为1.6×10-3 Nm2,比PET膜大3个数量级,颤振临界风速比同样长度的PET膜大5倍。PZT梁的自由端粘接PET膜,另一端用螺丝固定在铝底座上,用单面覆铜板与压电梁压接实现电极的引出。
| 表 1 微型风能收集器的结构尺寸 |
微型风能收集器在一个小型风洞中进行测试(见图 2),样机安装在风洞的夹具上,电极导线从夹具中引出。风洞的风速大小由变频器控制,在0~22 m/s范围内从小到大逐渐增加,由热线式风速仪测量(KIMO公司,CTV100)。样机的输出电压有效值由LeCroy公司的WaveSurf 422示波器测量,该示波器能够实时地进行FFT分析,方便观测压电梁的振动频率。微型风致振动能量收集器连接可变电阻R,用示波器测量电阻上的输出电压有效值VR,收集器的输出功率由公式P=VR2/R计算获得。调节电阻R,输出功率最大时对应的电阻为最优化负载Ropt。

|
图 2 微型风能收集器的测试系统与样机 |
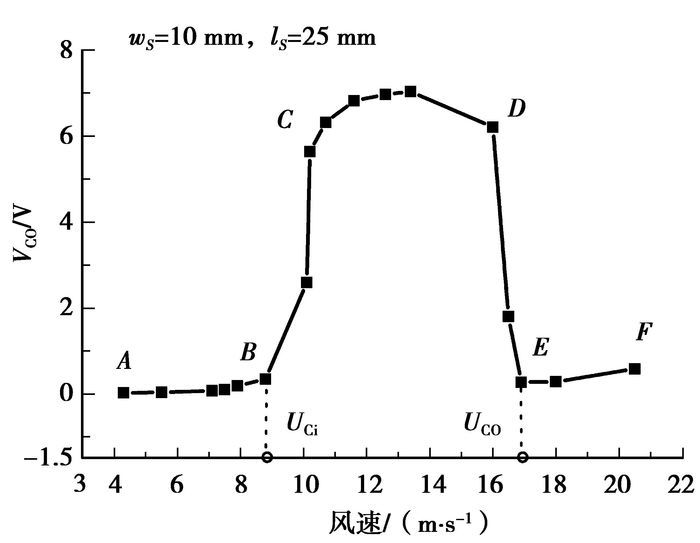
图 3为微型风能收集器的输出电压Voc随风速变化的曲线,可以看出随着风速增加,柔性梁的振动情况可明显地分成3个阶段,颤振发生在风速Uci与Uco之间的窗口范围内,这个2个风速分别称为切入临界风速和切出临界风速。
|
图 3 微型风能收集器输出电压随着风速增加的变化曲线 |
当风速小于Uci时,气动力对结构输入的能量小于结构阻尼消耗能量,结构是稳定的,不会引起颤振。由于气动力的扰动,柔性梁在中间平衡位置(图 1中虚线)作小幅度振动,对PZT梁的牵引力非常小,难使压电梁发生大的振动变形。因此收集器的开路电压Voc比较小,不大于1 V,如图 3中AB段。
当风速增到颤振切入临界风速Uci时,气动力的输入能量可抵消结构自身消耗,结构达到一个临界状态。微小的气动力扰动下,柔性梁就会突然失去稳定而触发颤振。该过程非常明显,从小幅度振动突然转变为大幅度的非线性摆动(颤振)。在颤振发生时,柔性梁与风载荷之间发生强烈的耦合,对压电悬臂梁的牵引力大大增强,收集器的输出电压明显增加,如图 3中CD段。
随着风速继续增加,当风速达到切出临界风速Uco时,轴向的气动力使PET膜发生发散现象,PET膜被突然吹向一侧,无法弹回初始的平衡位置,输出电压会突然下降。之后随着风速增加,柔性梁在一侧小幅度振动,收集器开路电压会逐渐增大,如图 3中的EF段。
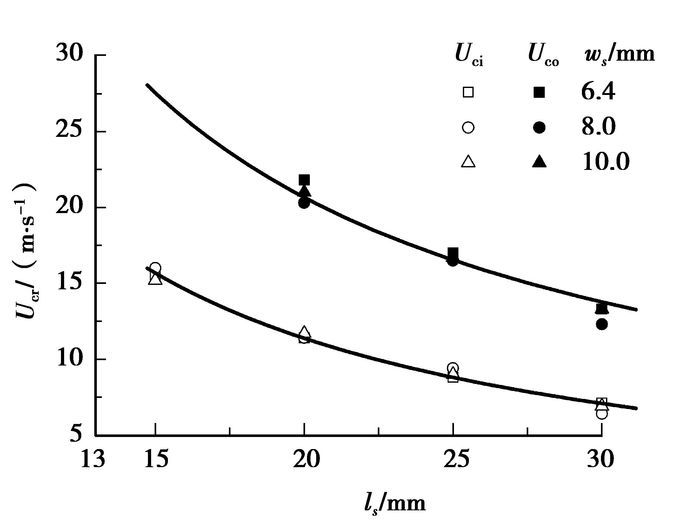
3.2 临界风速图 4为微型风能收集器的颤振切入临界风速Uci和切出临界风速Uco(ls=15 mm时,Uco超过仪器测量)。临界风速与柔性梁长度成反比,Uci和Uco都随柔性梁长度增加而减小,宽度的影响较小。当ws=8.0 mm、ls=30 mm时,临界风速Uci最小为6.4 m/s,Uco为12.3 m/s。采用公式(1)对数据进行拟合得到3组器件的切入与切出折合临界风速U0如表 2所示,其平均值分别4.46和8.08,图 4中实线即为折合临界风速平均值所得。从表 2可见发生颤振的风速窗口范围ΔU=Uco-Uci是Uci的0.81倍,试验值在0.76~0.93Uci之间。
|
图 4 柔性梁的颤振临界风速 |
| 表 2 临界风速的拟合参数 |
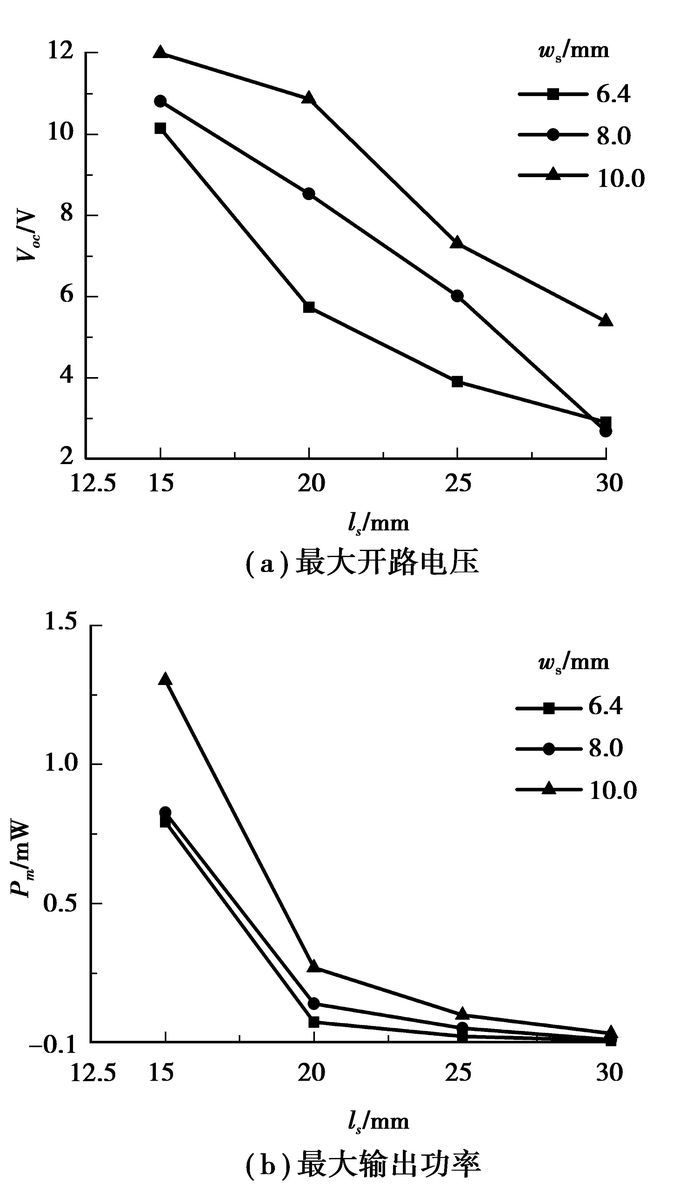
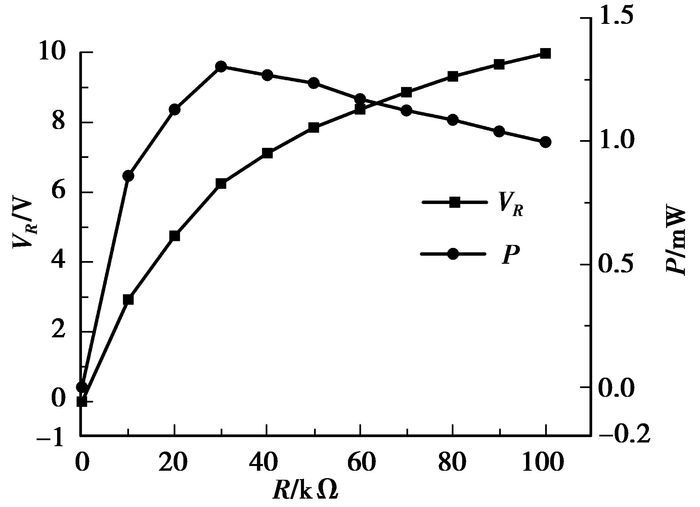
3组样机的最大开路电压Voc和最大输出功率Pm都是在柔性梁颤振的情况下测得,结果见图 5。可以发现,收集器的最大输出电压和功率随着柔性梁的长度增加而减小,随着宽度增加而增加。主要原因是长的柔性梁的切入临界风速小,收集器颤振时输入的风能小,导致输出性能低;宽柔性梁对PZT梁的牵引力大,增大了PZT梁的振幅,导致收集器的输出性能高。当ls=30 mm、ws=6.4 mm时输出性能最低,风速10 m/s,最大开路电压Voc=2.94 V,最大输出功率Pm=7.9 μW,最优化负载Ropt=500 kΩ;当ls=15 mm、ws=10 mm时输出性能最高,风速20.0 m/s时,输出电压和功率随负载电阻变化曲线见图 6,Voc=12.00 V,Pm=1 302.1 μW,Ropt=30 kΩ,功率密度为18.94 mW/cm3,比文献[9-12]中报道的大1~2个数量级。在安装柔性梁之前,单一的PZT悬臂梁在20.0 m/s风速下未触发颤振,风的扰动使其发生微弱的振动,开路电压为20 mV,输出功率只有6 nW,可见柔性梁结构能够显著增强PZT梁的风能获取能力。
|
图 5 微型风能收集器最大开路电压Voc和最大输出功率Pm的测试结果 |
|
图 6 微型风能收集器输出电压与功率随着负载的变化曲线 注:PET:ls=15 mm、ws=10 mm,风速:20 m/s |
结合风能收集器的临界风速与输出功率,要提高收集器的输出功率就应减小柔性梁的长度,但是同时切入临界风速也会提高。对ls=15 mm的柔性梁,切入临界风速达到了15.2 m/s(54.7 km/h),只能应用于汽车交通等特定环境。有2种解决方法,一是在保证输出功率满足设计要求的条件下降低收集器的临界风速。采用T型的柔性梁结构[16],将临界风速从11.7 m/s降到了5.4 m/s,输出功率降低了51%。另一种方法是通过外部的封装结构将入风的速度提高,如渐缩管等。这种方法对输出功率影响不大,但是会增加器件的体积。典型的温度和湿度无线传感网络节点[17]在915 MHz的频率下可以250 kbps的速率传输60~130 m的距离。工作周期为620 ms,其中传感器工作618 ms,传输数据2 ms,这2个过程中的功率分别为85、20 mW,1个周期消耗的能量为12.53 mJ。在不考虑管理电路损耗的情况下,微型风能收集器只需要9.6 s就能满足节点的一次数据采集与传输。
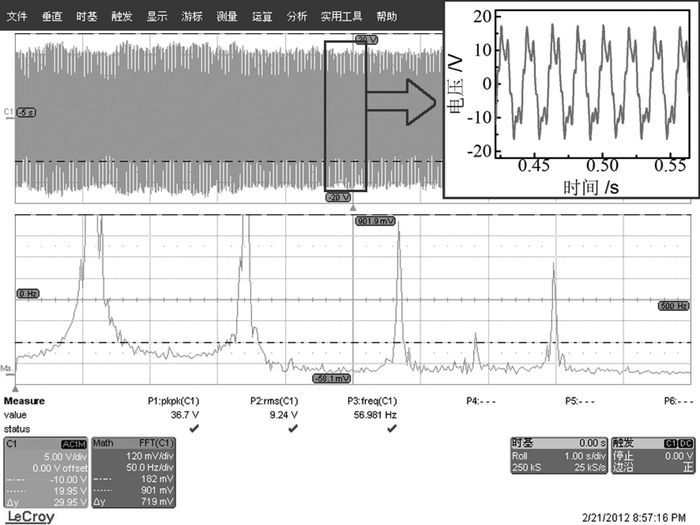
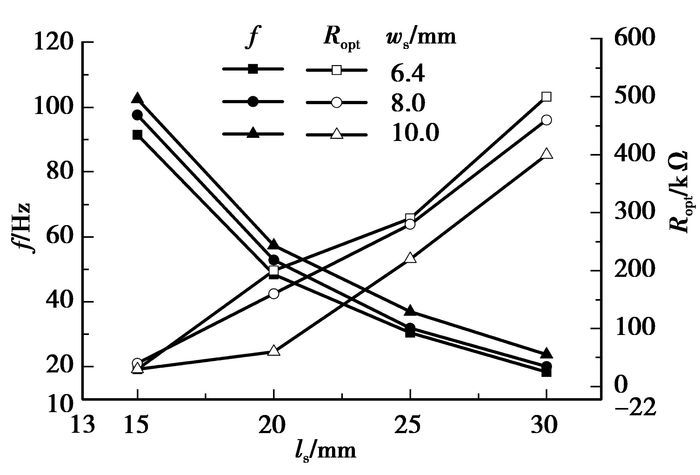
3.4 频率特性PZT梁的振动频率与最优化负载成反比[2],对能量收集器的输出功率影响很大,可以通过FFT分析得到收集器的频率特性。如图 7所示,在颤振状态下,风能收集器的输出电压是由若干个频率一定的正弦波叠加而成。从频谱图上可见这些频率是某一基频f及其整数倍频nf,其中高倍频成分主要是由于柔性梁的非线性摆动引起的。图 8为3组样机在刚触发颤振时的基频,可见颤振基频随着长度增加而减小,随着宽度增加而增加。因此柔性梁越短,最优化负载Ropt越小,提高了收集器的输出功率。此外,在Uci~Uco范围内,颤振基频随着风速增加而逐渐减小,与文献[14]结果一致。当ls=15 mm、ws=10 mm时,f从102.5 Hz降到84.2 Hz,减小了17.9%。
|
图 7 颤振状态下微型风能收集器输出电压波形图和FFT图 |
|
图 8 触发颤振时的基频与最优化负载 |
设计了基于柔性梁颤振机理的压电式微型风能收集器,通过风洞实验研究了收集器的气动特性和电学输出特性。结果表明:
1) 柔性梁的颤振发生在切入临界风速与切出临界风速之间的窗口范围内。得到了切入与切出临界风速的经验公式,其折合临界风速分别为4.46和8.08。
2) 柔性梁结构解决了PZT梁临界风速高的问题,显著增强了PZT梁风能获取的能力,提高了微型风能收集器的输出功率,最大输出功率达到1.30 mW,能够实现无线传感网络节点的供电。
| [1] | Roundy S, Wright P K, Rabaey J. A study of low level vibrations as a power source for wireless sensor nodes[J]. Computer Communications, 2003, 26(11): 1131–1144. DOI:10.1016/S0140-3664(02)00248-7 |
| [2] | Chen S N, Wang G J, Chien M C. Analytical modeling of piezoelectric vibration-induced micro power generator[J]. Mechatronics, 2006, 16(7): 379–387. DOI:10.1016/j.mechatronics.2006.03.003 |
| [3] | Aladwani A, Arafa M, Aldraihem O, et al. Cantilevered piezoelectric energy harvester with a dynamic magnifier[J]. Journal of Vibration and Acoustics, Transactions of the ASME, 2012, 134(3): 1–10. |
| [4] | Wischke M, Masur M, Kr ener M, et al. Vibration harvesting in traffic tunnels to power wireless sensor nodes[J]. Smart Materials & Structures, 2011, 20(8): 1–8. |
| [5] | Cepnik C, Radler O, Rosenbaum S, et al. Effective optimization of electromagnetic energy harvesters through direct computation of the electromagnetic coupling[J]. Sensors and Actuators A:Physical, 2011, 167(2): 416–421. DOI:10.1016/j.sna.2011.01.023 |
| [6] | Dittrich T, Belaidi A, Ennaoui A. Concepts of inorganic solid-state nanostructured solar cells[J]. Solar Energy Materials and Solar Cells, 2011, 95(6): 1527–1536. DOI:10.1016/j.solmat.2010.12.034 |
| [7] | Wang Z Y, Leonov V, Fiorini P, et al. Realization of a wearable miniaturized thermoelectric generator for human body applications[J]. Sensors and Actuators A:Physical, 2009, 156(1): 95–102. DOI:10.1016/j.sna.2009.02.028 |
| [8] | Herrault F, Ji C H, Allen M G. Ultraminiaturized high-speed permanent-magnet generators for milliwatt-level power generation[J]. Journal of Microelectromechanical Systems, 2008, 17(6): 1376–1387. DOI:10.1109/JMEMS.2008.2004854 |
| [9] | Pobering S, Ebermeyer S, Schwesinger N. Generation of electrical energy using short piezoelectric cantilevers in flowing media[C]//Proceedings of SPIE, March 8, 2009, San Diego, California, USA.[S.l.]:SPIE, 2009, 7288:728807. |
| [10] | Akaydin H D, Elvin N, Andreopoulos Y. Wake of a cylinder:a paradigm for energy harvesting with piezoelectric materials[J]. Experiments in Fluids, 2010, 49(1): 291–304. DOI:10.1007/s00348-010-0871-7 |
| [11] | Kwon S D,. A T-shaped piezoelectric cantilever for fluid energy harvesting[J]. Applied Physics Letters, 2010, 97(16): 164102–164102-3. DOI:10.1063/1.3503609 |
| [12] | Li S G, Yuan J P, Lipson H. Ambient wind energy harvesting using cross-flow fluttering[J]. Journal of Applied Physics, 2011, 109(2): 026104–026104. DOI:10.1063/1.3525045 |
| [13] |
王天雄.
略论现代大型悬索桥的力学特性[J]. 西北水电, 2004(2): 57–60.
WANG Tianxiong. On mechanial performance of modern large suspension bridge[J]. Northwest Water Power, 2004(2): 57–60. (in Chinese) |
| [14] | Tang L, Païdoussis M P. On the instability and the post-critical behavior of two-dimensional cantilevered flexible plates in axial flow[J]. Journal of Sound and Vibration, 2007, 305(1/2): 97–115. |
| [15] | Eloy C, Souilliez C, Schouveiler L. Flutter of a rectangular plate[J]. Journal of Fluids and Structures, 2007, 23(6): 904–919. DOI:10.1016/j.jfluidstructs.2007.02.002 |
| [16] | Zhao X Q, Wen Z Y. Piezoelectric wind generator based on T shape flexible beam fluttering[EB/OL].[2011-12-23]. http://cap.ee.ic.ac.uk/~pdm97/powermems/2011/poster/p_o2.pdf. |
| [17] | Yu H, Yue Q Q. Indoor light energy harvesting system for energy-aware wireless sensor node[J]. Energy Procedia, 2012, 16(B): 1027–1032. |
 2013, Vol. 36
2013, Vol. 36


