1b. 重庆大学 光电技术及系统教育部重点实验室, 重庆 400044;
2. 第三军医大学 野战外科研究所, 重庆 400042
1b. Key Lab of Optoelectronic Technology and Systems, Ministry of Education, Chongqing University, Chongqing 400044, China;
2. Research Institute of Surgery, Third Military Medical University, Chongqing 400042, China
神经元受到刺激后能够产生兴奋,这种兴奋通常以生物电的形式存在,并且能够穿透细胞膜进行传递,这形成了生物体中信号的传导。剑桥大学的生理学家霍奇金(alan hodgkin)和赫胥黎(andrew huxley)通过对大西洋枪乌贼神经轴突细胞中电脉冲传导的研究[1],总结出一套能够有效描述细胞膜电位变化以及通道电导和跨膜电流密度关系的数学模型,即H-H方程[2-3],该模型与实验结果精确吻合,为该领域后续的相关研究奠定了坚实的基础。
随着对神经系统研究的深入,人们逐渐认识到轴突不仅是神经元的被动输出单位,同时在信号处理和聚合物中起到主动作用。以往研究由于技术条件的限制,更多是依靠实验手段直接对神经轴突细胞的电传导特性进行研究。玻璃电极、金属丝电极、电压钳以及膜片钳和微电极阵列等记录技术都先后成功应用于神经纤维动作电位的研究,但这种常规实验方法需要提供活的生物样本,成本高且操作也较为复杂。数学建模分析方法也被广泛应用于神经电生理特性的研究,如Kuznetsov、Mestrom等人都先后利用MATLAB工具对电压门控通道进行仿真[4-5]。这类研究多采用解析方法进行求解,往往忽略了神经细胞的解剖特征。随着计算机科学的发展和有限元方法的不断成熟,人们更期于利用计算机建立神经元的仿真模型,用数值分析方法模拟和计算神经细胞神经冲动的传导。Johannes等人利用有限元方法对神经元冲动传导进行了一维和二维建模[6],所建的模型虽然综合了神经元解剖结构的形态特征,但总的来说,上述研究都无法逼真地描述神经细胞作为一个三维几何实体在电兴奋传导中电场的时间空间演变特点。
基于此,笔者尝试采用有限元仿真技术,利用COMSOL有限元分析工具,建立海马神经元轴突三维有限元模型,对轴突电刺激响应进行数值模拟,探讨神经细胞动作电位的非线性时变特性,以可视化方法描述神经元轴突三维实体中得电势时空分布特点。这种对神经元微观电活动的仿真研究在国内外尚未见报道,能够为细胞生物电传导的深入研究提供新生的研究模型和分析方法。
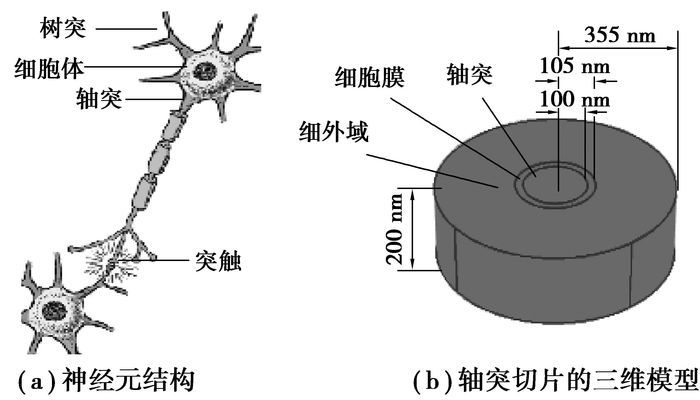
1 建模与方法 1.1 神经元轴突的几何模型神经元也称神经细胞,是构成高等生物神经系统的基本功能单位,如图 1(a)所示,它包括细胞体、轴突和树突[7]。
|
图 1 神经元结构及轴突模型 |
轴突是动物神经元将神经兴奋传导至神经细胞外部的输出通道。每个神经元只有一个轴突,轴突直接与细胞体相连,是从细胞体引出的呈圆柱体形状的细长突起。由于轴突的结构细长、表面光滑且分支较少,在较短的长度内,可以认为轴突的几何形状是标准的圆柱体。如图 1(b)所示,截取厚度为200 nm的轴突薄切片,它由3个部分组成,在求解中分为3个求解域。从内到外分别是轴突、细胞膜和细胞外域,它们的几何尺寸见表 1所示。
| 表 1 轴突切片模型的几何尺寸 |
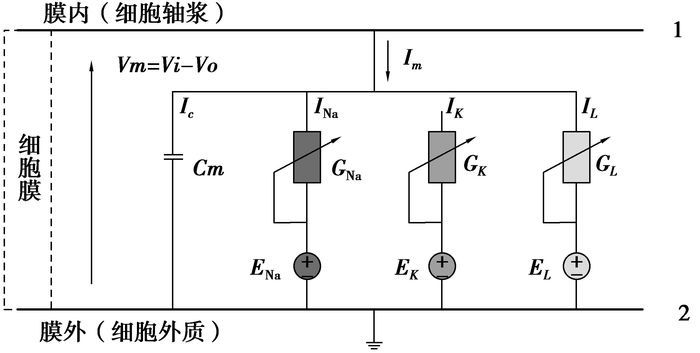
H-H方程指出,可以将细胞膜等效为平行板电容器,而细胞膜本身并非是完全绝缘的,其中含有许多可供离子通过的蛋白质通道,这些离子通道的开闭则受到细胞膜内外的电势差控制。由于细胞内外充满着含有各种离子的导电液体,可以将整个细胞切片看作导体,对单个细胞而言,则满足电流守恒的条件。因而,生物细胞膜的电传导特性可以用图 2所示的等效集总参数电路表示[8]。
|
图 2 H-H方程的等效电路 |
边界1和边界2分别表示细胞膜的内侧与外侧,中间区域则表示细胞膜。如图 2所示,流经细胞膜的电流Im主要由两项电流组成,一项是流过电容的电流Ic,另一项是离子电流Iion。离子电流Iion包含钠离子电流INa、钾离子电流IK和漏导电流IL(主要由氯离子引起)3项。Cm为膜电容,在模型大小尺寸确定的情况下,它的值是确定的。GNa,GK,GL分别是钠电导、钾电导和漏电导[9-10],其中GNa和GK是随跨膜电势变化的量,受到膜内外电势差控制,时时变化,而GL较小,可认为是常量。ENa、EK和EL分别是由各种离子浓度梯度所引起的电势差,称为Nernst电势。在特定的细胞中,细胞膜内外离子浓度相对稳定,离子的跨膜电位差由Nernst公式给出
| $ {E_X} = \frac{{RT}}{F}\ln \frac{{{{\left[ X \right]}_o}}}{{{{\left[ X \right]}_i}}}, $ | (1) |
式中:X表示离子的种类,[X]i和[X]o分别指膜内和膜外的离子浓度,R是气体常数,T是绝对温度,F是法拉第常数。由公式(1)可以得到模型中各种离子的Nernst电势,其具体数值以及模型中需要用到的相关参数详见表 2[11-12]。根据图 2,流经细胞膜的电流Im可表示为
| 表 2 模型中需要用到的参数 |
| $ {I_m} = {I_c} + {I_{{\rm{ion}}}}, $ | (2) |
膜电容电流
| $ {I_{{\rm{ion}}}} = {G_{{\rm{Na}}}}\left( {{V_m} - {E_{{\rm{Na}}}}} \right) + {G_K}\left( {{V_m} - {E_K}} \right) + {G_L}\left( {{V_m} - {E_L}} \right)。$ | (3) |
因此,由图 2的全电路欧姆方程,公式(2)可表示为
| $ \begin{array}{*{20}{c}} {{I_m} = {C_m}\frac{{{\rm{d}}{V_m}}}{{{\rm{d}}t}} + {G_{{\rm{Na}}}}\left( {{V_m} - {E_{{\rm{Na}}}}} \right) + }\\ {{G_K}\left( {{V_m} - {E_K}} \right) + {G_L}\left( {{V_m} - {E_L}} \right)。} \end{array} $ | (4) |
为了便于后面的有限元建模,式(4)[13]可以变形为
| $ \begin{array}{*{20}{c}} {\nabla \cdot \left[ {\frac{{\partial \left( {{\varepsilon _k}\nabla V} \right)}}{{\partial t}} + {\sigma _k}\nabla V} \right] = {J_m},区域\;Da \cup De,}\\ {\nabla \cdot \left\{ {\frac{{\partial \left( {{\varepsilon _k}\nabla V} \right)}}{{\partial t}} + \left[ {{\sigma _k}\nabla V - Je \cdot \mathop r\limits^ \wedge } \right]} \right\} = {J_m},区域\;Dm,}\\ {Je = {G_{{\rm{Na}}}}{E_{{\rm{Na}}}} + {G_K}{E_K} + {G_L}{E_L},} \end{array} $ | (5) |
式中:Jm表示是通过膜的电流密度大小;Je表示各种离子经离子通道流动而引起的电流密度大小,反映离子在膜内外的流动而引起细胞膜上的电势扰动。εk和σk(k∈{a, m, e})分别表示轴突区域(a)、膜区域(m)和细胞外域(e)部分(分别用Da、Dm和De表示)的相对介电常数和电导率。在轴突和细胞外域部分(不含膜),充斥着含有各种带电离子的液体,在这2个区域,电导率σ和介电常数ε可以视为常数,其值在表 2中给出。在细胞膜区域,介电常数εm和电导率σm分别被定义为
| $ {\varepsilon _m} = \frac{{{C_m}{d_m}}}{{{\varepsilon _0}}}, $ | (6) |
| $ {\sigma _m} = {G_m} \cdot {d_m}, $ | (7) |
其中Gm是细胞膜的电导,被定义为钠离子电导、钾离子电导和漏电导的函数
| $ {G_m} = {G_{{\rm{Na}}}} + {G_K} + {G_L}。$ | (8) |
由于漏电导GL较小,可以认为是常数,而离子电导GNa和GK是跨膜电势Vm的函数。根据H-H方程,钾离子电导和钠离子电导服从下列式子
| $ {G_K} = {{\bar g}_K}{n^4}; $ | (9) |
| $ {G_{{\rm{Na}}}} = {{\bar g}_{{\rm{Na}}}}{m^3}h。$ | (10) |
n,m,h称作活化变量,服从下列微分方程
| $ \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = {\alpha _x} \cdot \left( {1 - x} \right) - {\beta _x} \cdot x,其中\;x \in \left\{ {n,m,h} \right\}, $ | (11) |
α和β称为压控转移速率系数(voltage-dependent transfer rate constants),分别反映离子通道“由闭到开”和“由开到闭”的转移速度,其表达式在表 3中列出。
| 表 3 转移速率系数的表达式 |
在COMSOL Multiphysics中,按照图 1(b)所示进行几何建模,选择电流模块和广义型PDE模块,并且根据图 1(b)建立神经元轴突的三维几何模型,根据公式(5)和(11)分别设定电流模块和PDE模块的相关物理参数[14-15]。求解前需对模型进行网格剖分,网格划分采用自由划分四面体网格,计算区域的网格单元数为31 739,最小单元质量为0.046 53。
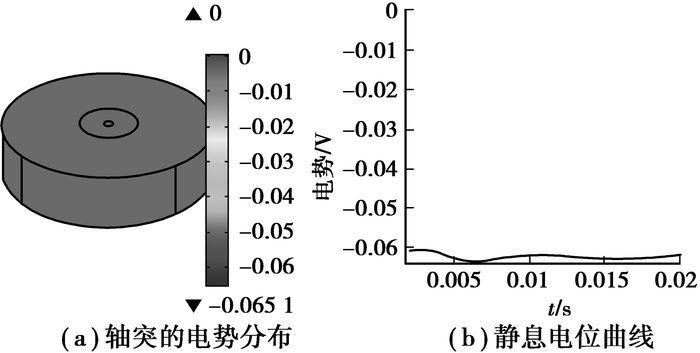
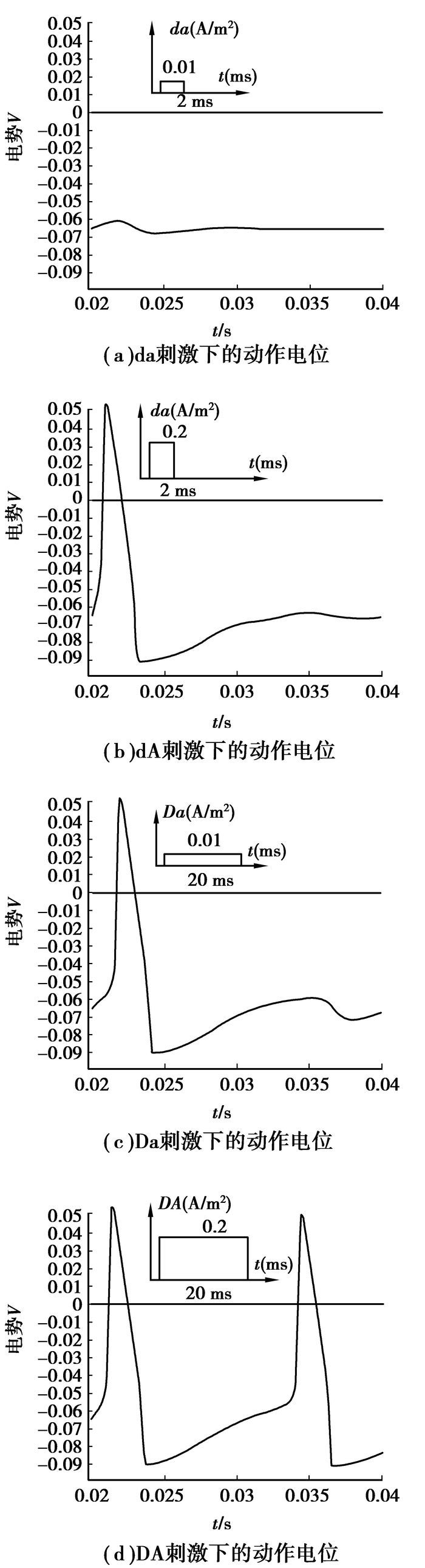
1.3 施加刺激电流及求解通过COMSOL Multiphsics提供的边界电流源选项能够非常方便的给神经轴突施加电流刺激,首先在模型定义中定义4种不同的电流密度刺激:a(2 ms, 0.01 A/m2)、dA(2 ms, 0.2 A/m2)、Da(20 ms, 0.01 A/m2)和DA(20 ms, 0.2 A/m2),然后在求解过程中,利用瞬态求解器分两次求解,第一次求解不施加刺激电流,得到细胞的静息电位曲线,如图 3(b)所示,给细胞膜的内部区域施加不同的刺激电流(即往轴突模型的几何中轴线注入不同的刺激电流),分别设置轴突内部的边界电流源为da、dA、Da和DA,再次求解,得到图 4所示的动作电位曲线。
|
图 3 轴突电势分布及电位曲线 |
|
图 4 (a)(b)(c)(d)分别表示在电流密度刺激da, dA, Da, DA作用下的动作电位图 |
图 3(a)给出了轴突切片模型的体电势分布,模型的上下表面电绝缘,细胞外域接地,图中表明,细胞膜内侧电势约为-65 mV,细胞外域电势趋于0。神经细胞在未受到电流刺激时,内侧电势比外侧电势高-65 mV,这个电势差即为静息电位,如图 3(b)所示。
2.2 不同刺激下的动作电位曲线通过对模型施加不同的电流密度刺激da:(2 ms,0.01 A/m2)、dA:(2 ms,0.2 A/m2)、Da:(20 ms,0.01 A/m2)、DA:(20 ms,0.2 A/m2),刺激电流均在0.01 s时刻加入,得到了如图 4(a)(b)(c)(d)所示的细胞膜上的电位响应,从图中可分析出:结果1:(a)没有产生完整的动作电位,只是在静息电位的基础上有些许的扰动,(b)(c)(d)产生了完整的动作电位,动作电位的幅度从-65 mV至+35 mV,动作电位的持续时间约为2 ms;结果2:比较(a)和(b)、(a)和(c),较短的刺激时间、高幅度的电流脉冲或者增加刺激时间、减小电流脉冲均可以产生动作电位;结果3:比较(b)(c)(d)可以看出,它们的峰值出现的时刻不一样,(b)和(c)的电势峰值分别出现在0.012 s和0.017 s,(d)分别在0.012 s和0.022 s时刻产生了2个波峰。
3 结论以上结果1和结果2表明:对于动作电位的产生,细胞受到的刺激需要达到一个阈值,刺激时间过短或是刺激脉冲过小都不能使细胞达到阈上刺激,阈下刺激不能触发完整的动作电位,但是能引起膜上电势的小幅度扰动,生理学上解释为阈下刺激同样会引起少量钠离子内流,产生小幅度的去极化,不过这种去极化不足以使膜电位达到阈电位水平,所以体现为膜上的电势小幅度波动。若想要达到能够触发动作电位的阈值,可以通过增加刺激的持续时间和提高刺激电流的幅度。结果3表明:较强幅度的电流脉冲会导致细胞膜上电势的快速响应,在同为阈上刺激的条件下,电流密度较大的刺激脉冲诱发的动作电位峰值出现时刻较早,而且可能引起多个动作电位的产生。值得注意的是,为了便于几何建模,截取厚度为200 nm的神经轴突进行建模(近似于圆柱体),实际上这个轴突模型厚度数值与文献报道的真实数据是基本相符的;另外,本文重点关注电流在神经轴突上的径向传导,且注入刺激电流的部位在模型几何中心,因此模型厚度对数值分析结果的影响可以忽略。
数值模拟神经元轴突的神经冲动传导,探索了神经冲动穿透细胞膜的传导机理。用麦克斯韦静态电流守恒方程,结合H-H方程,用有限元方法进行数值求解。按照生理学的相关理论,动作电位的电压变化范围是-70~0 mV,神经纤维动作电位的持续时间一般为0.5~2.0 ms,所建立的有限元模型与实际相吻合,这为深入研究生物神经冲动的传导及细胞修复奠定了良好的基础。
| [1] | Hodgkin A L, Huxley A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. Journal of Physiology, 1952, 117(4): 500–544. DOI:10.1113/jphysiol.1952.sp004764 |
| [2] | 汪云九, 等. 神经信息学[M]. 北京: 高等教育出版社, 2006: 20-22. |
| [3] | 徐玉东, 王建红. 人体解剖生理学[M]. 北京: 人民卫生出版社, 2007: 18-21. |
| [4] | Riet A. A continuation toolbox in MATLAB, Master Thesis, Mathematical Institute, Utrecht University[M], The Netherlands, 2000. |
| [5] | Govaerts W. Numerical Continuation of Bifurcations of Limit Cycles in MATLAB[J]. Siam Journal on Scientific Computing, 2005, 27(1): 231–252. DOI:10.1137/030600746 |
| [6] | Martinek J. A Novel approach to simulate Hodgkin-Huxley-like excitation with COMSOL multiphysics[J]. Artificial Organs, 2008, 32(8): 614–619. DOI:10.1111/aor.2008.32.issue-8 |
| [7] | Gray E G. The fine structure of nerve[J]. Comparative Biochemistry and Physiology, 1970: 419–422. |
| [8] | 丁光宏, 顾全保, 主译. 电生理学基础[M]. 上海: 复旦大学出版社, 2005: 18. |
| [9] | Hille B. Ionic channels in nerve membranes[J]. Progress in Biophysics and Molecular Biology, 1970, 21: 1–32. DOI:10.1016/0079-6107(70)90022-2 |
| [10] | Hille B. Ionic channels of excitable membranes:Current problems and biophysical approaches[J]. Biophysical Society, 1978, 22(2): 283–294. DOI:10.1016/S0006-3495(78)85489-7 |
| [11] | Courtney L. Computational modeling of three-dimensional electrodiffusion in biological systems:Application to the node of ranvier[J]. Biophysical Journal, 2008, 95(6): 2624–2635. DOI:10.1529/biophysj.108.132167 |
| [12] | Noble D, Garny A, Noble P J. How the Hodgkin-Huxley equations inspired the cardiac physiome project[J]. Journal of Physiology, 2012, 590(11): 2613–2628. DOI:10.1113/jphysiol.2011.224238 |
| [13] | Elia S. A finite element model for the axon of nervous cells[J]. COMSOL Conference 2009, October 14-162009, Milan, Italy |
| [14] | Moulin C. A new 3-D finite element model based on thin-film approximation for microelectrode array recording of extracellular action potential[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(2): 683–692. DOI:10.1109/TBME.2007.903522 |
| [15] | Mclntyre C C. Cellular effects of deep brain stimulation:Model-based analysis of activation and inhibition[J]. Journal OF Neurophysiology, 2004, 91(4): 1457–1469. DOI:10.1152/jn.00989.2003 |
 2013, Vol. 36
2013, Vol. 36

