“信息爆炸”使得从网络获取有用信息遇到一些瓶颈问题,如用户就某个主题搜索特定信息,结果却找到大量不相关的网页等[1]。解决这些问题的有效方法之一是通过遍历网页,收集与某个主题相关的文档并找出这些文档与该主题之间的可能联系,而这必定需要一个用于判定某个网页是否与特定主题相关的分类机制[2]。相对于人工分类,自动网页分类的成本更低,速度更快,因而随着网络资源的持续增长,自动分类的重要性变得越来越明显。自动网页分类是一个有监督的学习过程,通过一组加了标签的网页来训练分类器,然后用分类器为待分类的网页加上一个预定义的标签[3]。由于在海量的网页信息资源中,绝大多数信息以文本形式存在,因此自动网页文本的分类技术成为最具研究意义的网页分类热点问题之一。
近年来许多研究者将模式分类技术应用到网页文本分类问题中,于是出现了大量应用于网页文本分类的模型和学习技术。此外,还出现了一些针对中文网页分类的技术,如基于线性的分类器即向量空间模型(vector space model,VSM)[4]、神经网络模型[5]等,其中VSM因简单而广泛用于自动文档分类。基于VSM进行网页文本数据分类时,通常先将文本抽象为一个矩阵,然后针对所构造的矩阵进行分类训练。文本分类器常常采用决策树[6]、K最近邻(K-nearest neighbor, KNN)[7]、神经网络[8]、朴素贝叶斯[9]、支持向量机[10]等机器学习方法,这些方法适用于特征数较少的分类问题,在对高维文本特征矩阵进行分类训练时通常效率较低,而网页文本数据经过抽象得到的是高维矩阵,因而上述方法直接用于求解网页分类问题时,其性能往往受到影响。针对这个问题,可通过先对高维文本特征矩阵降维,减小问题规模,降低问题复杂度,再进行分类学习的方法来提高求解效率。常用的数据降维方法有奇异值分解(singular value decomposition, SVD)[11]、NMF[12]等算法。SVD算法将原矩阵分解为3个矩阵的乘积形式,NMF算法通过简单迭代计算将原矩阵分解为2个矩阵的乘积,前者执行时间较长且分解过程较繁琐,而后者求解过程相对简单,分解所得的左右非负矩阵占用的存储空间相对较小且语义解释性强,因而适用于处理规模较大的问题[13]。在用NMF进行矩阵分解时一般需要对分解后的2个矩阵进行初始化,而且要通过复杂的更新规则来提高降解矩阵的稀疏度,以提高模型的区分能力。研究采用一种基于NMF的归一化压缩(NCMF)的矩阵分解算法[14],此方法只需初始化一个矩阵且采用的迭代更新规则更简单。
在VSM中常存在大量难以用“有”或“无”来明确定义其与文本相关性的特征词,而且文本中也包含一些语义多样的词汇,常使得难以明确判断文本与类别是“有关”还是“无关”,因而直接对VSM的高维确定性矩阵进行分类通常效果也不理想。针对此问题,在所提出的分类模型中分别引入模糊相似度来计算特征词与文本及类别的相关系数,以获得更好的分类效果。
1 结合NCMF的模糊网页分类算法假定P={p1,p2,…,pn}表示n个网页文档构成的文本集,W={w1,w2,…,wm}表示特征词集,类别集合为C={c1,c2,…,cc}。训练样本集由已标注类别的文本组成,即T={<pj,c(pj)>|pj∈P,c(pj)∈C,1≤j≤n},其中c(pj)表示网页文本pj所属的主题类别。
1.1 构造向量空间模型构建VSM是将网页文本数据转化为计算机可识别格式的有效方法之一,研究采用TF-IDF方法,该方法综合考虑各词在相应文本及其他类别主题中分别出现的次数,具有较好的区分特性[15]。这里,每个网页文本pj表示为一个向量Φj={φj1,φj2,…,φjm},φji(wi,pj)表示特征词wi在pj中的权重,其计算公式如下
| $ {\varphi _{ji}} = \frac{{{f_{ji}} \times \log \left( {\frac{n}{{{n_i}}}} \right)}}{{\sqrt {\sum\nolimits_{i = 1}^m {{{\left( {{f_{ji}} \times \log \left( {\frac{n}{{{n_i}}}} \right)} \right)}^2}} } }}, $ | (1) |
其中:fji表示wi在pj中出现的次数;n表示网页文本总数,ni为含有wi的网页文本数。于是基于文本集P可构造一个n×m的词文本权重矩阵Φ(W,P)=(Φ1,Φ2,…,Φn)T。
1.2 基于NCMF的特征约简在文本分类中,不需要精确区分文本的每个细节,只需获得该文本在总体上的类别倾向,因此直接基于稀疏的VSM进行文本分类必然产生数据冗余并导致大量的资源消耗[16]。针对这个问题,可以将这个高维稀疏矩阵向低维紧凑语义空间进行映射,以削减空间维数,找出最具代表性的特征[17]。这里可用NMF算法进行特征提取,将高维词文本矩阵Φ分解为2个非负矩阵的乘积,即Φ=VH,左矩阵V可看作数据的压缩形式,右矩阵H可看作描述不同维映射关系的投影矩阵,并以KL散度作为相似度衡量,其目标函数如公式(2)所示
| $ \begin{array}{l} F\left( {\mathit{\boldsymbol{V}},\mathit{\boldsymbol{H}}} \right) = \\ \mathop {\min }\limits_{V \ge 0,H \ge 0} \sum\nolimits_i {\sum\nolimits_j {\left( {{\varphi _{ij}} \cdot \lg \frac{{{\varphi _{ij}}}}{{{{\left( {\mathit{\boldsymbol{VH}}} \right)}_{ij}}}} - {\varphi _{ij}} + {{\left( {\mathit{\boldsymbol{VH}}} \right)}_{ij}}} \right)} } , \end{array} $ | (2) |
其中:Φ∈Rn×m,V∈Rn×r,H∈Rr×m,1≤i≤m,1≤j≤n,r为低维空间的维数,一般满足(n+m)≪n×m。由于分解前后的矩阵中仅包含非负元素,因此Φ的任一行向量也可解释为H中所有向量(称为基向量)的加权和,即
| $ {\mathit{\boldsymbol{V}}_{ik}} \leftarrow {\mathit{\boldsymbol{V}}_{ik}}\frac{{\sum\nolimits_{j = 1}^m {\frac{{{\mathit{\boldsymbol{H}}_{kj}} \cdot {\varphi _{ij}}}}{{\left( {\sum\nolimits_{k' = 1}^r {{\mathit{\boldsymbol{V}}_{ik'}}{\mathit{\boldsymbol{H}}_{k'j}}} } \right)}}} }}{{\sum\nolimits_{j' = 1}^m {{\mathit{\boldsymbol{H}}_{k'j}}} }}, $ | (3) |
| $ {\mathit{\boldsymbol{H}}_{kj}} \leftarrow {\mathit{\boldsymbol{H}}_{kj}}\frac{{\sum\nolimits_{i = 1}^m {\frac{{{\mathit{\boldsymbol{V}}_{ik}} \cdot {\varphi _{ij}}}}{{\left( {\sum\nolimits_{k' = 1}^r {{\mathit{\boldsymbol{V}}_{ik'}}{\mathit{\boldsymbol{H}}_{k'j}}} } \right)}}} }}{{\sum\nolimits_{i' = 1}^m {{\mathit{\boldsymbol{V}}_{ik'}}} }}, $ | (4) |
V和H随公式(3)和(4)的迭代计算将变得越来越稀疏,然而这2个对称的更新规则会使它们的稀疏趋势相互制约,并最终导致其失去明显的稀疏特征,而V、H特别是H的高稀疏性将有利于发现有意义的隐含特征,因而研究采用一种可有效提高H稀疏度的NCMF算法进行求解,假定Max_iter是预先设定的最大迭代次数,则算法过程描述如下。
Step1 按公式(5)归一化词文本矩阵Φ
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{ij}} \leftarrow \frac{{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{ij}}}}{{\sum\nolimits_{i' = 1}^m {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{i'j}}} }}; $ | (5) |
Step2 初始化r×m维的H矩阵,iter=1;
Step3 分别按公式(6)、(7)更新矩阵V、H
| $ {V_{ik}} \leftarrow \frac{{\sum\nolimits_{j' = 1}^m {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{ij'}}{\mathit{\boldsymbol{H}}_{kj'}}} }}{{\sum\nolimits_{j = 1}^m {{\mathit{\boldsymbol{H}}_{kj}}} }}, $ | (6) |
| $ {\mathit{\boldsymbol{H}}_{kj}} \leftarrow \sum\nolimits_{i = 1}^m {\left( {\frac{{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{ij}}}}{{\sum\nolimits_{k' = 1}^r {\left( {{\mathit{\boldsymbol{V}}_{ik'}}{\mathit{\boldsymbol{H}}_{k'j}}} \right)} }}{\mathit{\boldsymbol{V}}_{ik}}} \right){\mathit{\boldsymbol{H}}_{kj}}} ; $ | (7) |
Step4 若iter=Max_iter,结束; 否则,iter++,转step3。
从公式(6)和(7)可以看出,与NMF不同的是,这里V基于已知的Φ和当前H进行更新,而H基于Φ、V及H自身进行更新,所以NCMF在初始阶段只需初始化H,然后再基于此更新,且不对称的更新规则使得H在更新时几乎不受约束。这说明在NCMF算法中,不需通过显式的稀疏处理即可获得较稀疏的H。
训练集及测试集的文本通过NCMF特征提取方法降维后,得到一个低维语义空间中的向量。尽管各词在不同主题中出现的频度可以表明该词与各主题的相关性,但是由于没有考虑到语义信息,直接基于此权重矩阵进行分类的效果往往不尽理想,因而在本文的分类模型中进一步引入特征词与类别的模糊相关性分析,为后面分析文本及其类别间的相似度提供更多的语义信息。
1.3 特征与类的模糊隶属度由于特征词集能够表征数据集的主要特征,而基于特征词集可以得到数据集的类别属性,因而在特征词和类别之间存在某种相关性。首先采用隶属度矩阵Y(W, C)=(y1, y2, …, ym)T来定义特征词与类别间的相关性,其中yi(1≤i≤m)是一个c维的向量,即
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {{y_{11}}}& \cdots &{{y_{1c}}}\\ \vdots &{}& \vdots \\ {{y_{m1}}}& \cdots &{{y_{mc}}} \end{array}} \right], $ | (8) |
其中0≤yil≤1(1≤l≤c)表示特征词wi对类别cl(cl∈C)的隶属度。基于文献[18]中的讨论,综合考虑词在类别中出现的频率及特征词在文本集中的分布情况,采用如下定义
| $ {d_{il}} = \frac{{\left( {\sum\nolimits_{{w_i} \in {p_j} \wedge c\left( {{p_j}} \right) = {c_l}} {{f_{ji}}} } \right)}}{{\sum\nolimits_{l = 1}^c {{f_{ji}}} }}, $ | (9) |
| $ {y_{il}} = \frac{{{d_{il}} \times n_i^l}}{{{n^l}}}。$ | (10) |
在公式(9)中,dil是基于统计方法计算的wi在cl中出现的频率,fji表示wi在网页文本pj中出现的次数,若wi只在属于cl的文本中出现,则dil=1;若在多类的不同文本中出现,则dil值较小,dil的值可以反映wi在类别中的分布。在公式(10)中,yil为Y(W, C)中的元素,nil表示在cl中包含wi的文本数,nl表示cl中包含的文本总数,其计算公式为
| $ n_i^l = \left| {\left\{ {{p_j}\left| {c\left( {{p_j}} \right) = {c_l} \wedge {w_i} \in {p_j}} \right.} \right\}} \right|, $ | (11) |
| $ {n^l} = \left| {\left\{ {{p_j}\left| {c\left( {{p_j}} \right) = {c_l}} \right.} \right\}} \right|。$ | (12) |
由于在相应类中分布较均匀的特征词相对于只在个别文本中出现的特征词具有更好的区别能力,通过
通过词-文本矩阵Φ与Y的乘积可以获得各文本的类别隶属度矩阵X,即
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} Y}}, $ | (13) |
其中X的元素xjl(1≤j≤n,1≤l≤c)表示文本pj与cl隶属度。根据NCMF算法得到Φ的近似VH,公式(13)可改写为
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{VHY}}。$ | (14) |
令U=HY,则上式变为
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{VU}}, $ | (15) |
上式中的U可以解释为,对由NCMF算法得到的文本特征矩阵V所代表的新特征词集W′={w′1,w′2,…,w′r}和类别集合C的相关性描述,即U(W′,C)=(u1,u2,…,ur)T,其中uk(k=1,2,…,r)也是一个c维的向量,也即
| $ \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{u_{11}}}& \cdots &{{u_{1c}}}\\ \vdots &{}& \vdots \\ {{u_{r1}}}& \cdots &{{u_{rc}}} \end{array}} \right], $ | (16) |
其中ukl表示w′k对cl的隶属度,其计算公式为
| $ {u_{kl}} = \sum\nolimits_{i = 1}^m {{h_{ki}} \times {y_{il}}} 。$ | (17) |
将待分类文本q的词文本隶属向量Ψ=(Ψ1,Ψ2,…,Ψm)经NCMF降维转为一个低秩向量β=(β1,β2,…,βr),然后利用上节分类训练得到特征类模糊相关性矩阵U,按照公式(18)来计算q与C中cl的相似度
| $ {s_l}\left( {q,{c_l}} \right) = \frac{{\sum\nolimits_{k = 1}^r {\left( {\left( {{\beta _k} - {{\bar \alpha }_k}} \right) \times \left( {{u_{kl}} - {{\bar u}_l}} \right)} \right)} }}{{\sqrt {\sum\nolimits_{k = 1}^r {{{\left( {{\beta _k} - {{\bar \alpha }_k}} \right)}^2}} \times \sum\nolimits_{k = 1}^r {{{\left( {{u_{kl}} - {{\bar u}_l}} \right)}^2}} } }}, $ | (18) |
其中1≤l≤c,
通过计算q到所有类别的相似度,可得到类别模糊集
| $ c\left( q \right) = \mathop {\max }\limits_{1 \le l \le c} \left\{ {{\mathit{\boldsymbol{S}}_l}\left( q \right)} \right\}。$ | (19) |
基于上述讨论,给出提出的结合NCMF的模糊分类算法(fuzzy classifier combined with ncmf,NFC)流程如下
Step1 提取网页中的文本数据,进行预处理;
Step2 根据公式(1)构造训练文本集的向量空间模型,计算每个特征词与文本之间的模糊关系,生成词文本隶属度矩阵Φ=(Φ1,Φ2,…,Φn)T;
Step3 根据NCMF算法对Φ进行分解,根据公式(6)、(7)迭代求解得到压缩的词文本隶属矩阵V和投影矩阵H;
Step4 根据公式(9)和(10)计算训练集中特征类别的隶属度矩阵Y;
Step5 根据公式(16)和(17)计算针对降解的压缩矩阵V的词类别隶属矩阵U;
Step6 对于输入的待分类测试文本q,根据公式(1)构造m维隶属度向量Ψ,并通过NCMF算法转化为r维向量β;
Step7 根据公式(18)计算测试文本模糊集与各类别模糊集的相似度sl(q, cl),1≤l≤c,得到文本与类别的隶属度模糊集S(q);
Step8 根据公式(19)输出q的类别。
2 实验结果及分析从互联网随机抽取网页组成实验数据进行验证,在数据准备阶段,以环境、教育、经济、游戏和体育为主题(记为c1~c5)随机下载共1100个网页作为基础实验数据,各类文本数分布如表 1所示,从每类中随机抽取2/3的网页作为训练集,余下1/3作为测试集。
| 表 1 各主题文本数分布 |
由于中文不像英文通过空格来分词,因此需要对中文文本进行专门的分词处理,采用中科院计算所提供的汉语词法分析系统(ICTCLAS)进行分词,并由此得到一个词表。为了提高文本表征词典的质量以提高分类器训练的效率,将词表中的“停用词”过滤掉,并采用信息增益法[20]对文档进行特征词提取,,最后选取3 000(即m)个特征词来表达文本语义。通过实验确定了NCMF算法中的迭代次数Max_iter=100。
为评价分类算法的性能,采用最通用的性能评价方法:准确率Precision和召回率Recall。对于某个特定的类别,Precision指在分类器所标记的正样本中被正确分类的正样本所占的比例,Recall指被分类器正确分类的正样本占所有正样本的比例。Precision和Recall从不同角度反映了分类质量,但是二者必须综合考虑,不可偏废,因此通常采用Precision和Recall的加权调和平均,即F1测试值来评价分类算法的优劣[7]。F1的值越大,则表示分类器的性能越好。通常采用微平均Micro_F1(记为F1)值评价分类器在每一类上的性能,而采用宏平均Macro-F1值(记为
假定某个类cl的偶然事件表如表 2所示,其中“+”表示正样本即属于cl的样本,“-”表示负样本即不属于cl的样本,tp(tn)表示通过分类器正确分类的正(负)样本,fp(fn)表示错误分类的正(负)样本。
| 表 2 类cl的列联表 |
分类器在类cl上的微平均Precisionl和Recalll的计算公式分别如公式(20)和(21)所示
| $ {\rm{Precisio}}{{\rm{n}}_l} = t{p_l}/\left( {t{p_l} + f{p_l}} \right); $ | (20) |
| $ {\rm{Recal}}{{\rm{l}}_l} = t{p_l}/\left( {t{p_l} + f{n_l}} \right), $ | (21) |
类cl上的微平均F1l值的计算方法如公式(22)所示[7]
| $ {F_{1l}} = \frac{{2 \times {\rm{Precisio}}{{\rm{n}}_l} \times {\rm{Recal}}{{\rm{l}}_l}}}{{\left( {{\rm{Precisio}}{{\rm{n}}_l} + {\rm{Recal}}{{\rm{l}}_l}} \right)}}。$ | (22) |
在c个类别上的宏平均
| $ \overline {{F_1}} = \sum\nolimits_{l = 1}^c {{F_{1l}}/c} 。$ | (23) |
由于NCMF是NFC算法的重要步骤之一,而r是影响NCMF性能的主要参数,因而r也是NFC算法的重要参数。通过实验测试了不同的r值对算法
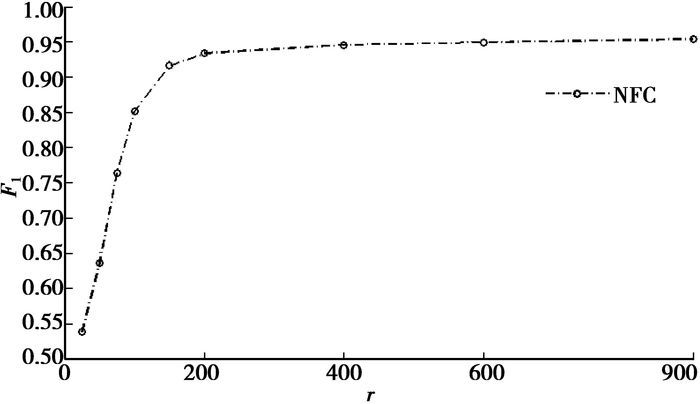
|
图 1 不同r值对NFC分类精度的影响 |
从图 1可以看出,不同的r值对NFC算法
为了验证NFC算法的有效性,选择KNN分类算法[7](实验中取k=5)、基于模糊关系的FRM算法[18]和基于SVD分解的LSI算法[19]进行比较。由于NCMF采用的随机初始化方法对分类结果有一定的影响,因此将算法运行20次,然后取20次运行结果的平均指标值进行比较。图 2给出了4种算法在5大主题上的分类结果的比较。
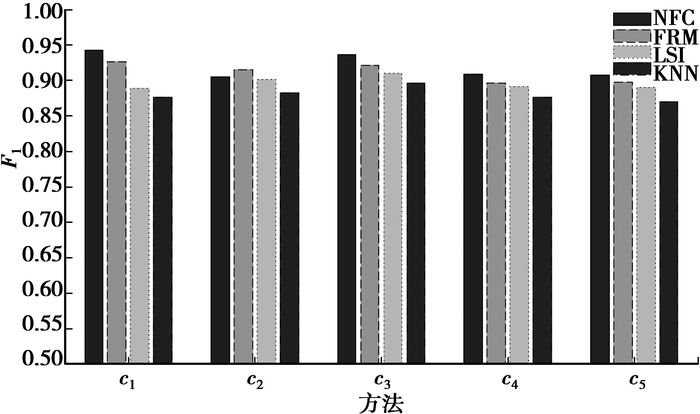
|
图 2 各类的F1值比较 |
从图 2可以看出,NFC只在类c2上的F1值劣于FRM算法,且在其他所有类别上的F1值均优于LSI和KNN算法。
表 3给出4种算法的
|
表 3 各算法的 |
从表 3可以看出,在4种算法中,采用模糊逻辑的NFC和FRM算法的分类准确度均优于另外2种方法,而NFC通过NCMF降维处理使其运行时间相对于FRM有了68%的改进,而且在
通过进一步分析可以发现,NFC虽然对表征样本的词文本权重矩阵采用NCMF进行了降维处理,但这种数据约简的方法并没有降低分类精度,且其分类性能指标值优于未采用降维处理的FRM算法。这说明在初始的权重矩阵中包含大量的冗余信息,直接对该矩阵进行分类学习的效果未必理想,而通过去除一定的冗余信息,反而找出了与文本语义更紧密的特征词,所得的系数矩阵可以作为代表原始样本的特征矩阵,基于此低维特征矩阵进行模糊分类训练可以提高分类准确率。LSI算法中虽然采用SVD矩阵分解方法进行降维,但其计算过程较NCMF复杂,运行时间较长,而且SVD分解所得的基向量元素中含有负值,不是真正的基于部分的分解,可解释性也较差。
3 结论采用一种基于NMF的改进算法,即NCMF算法,将高维的网页文本数据映射到低维语义空间。NCMF只需要初始化投影矩阵,且不对称的更新规则可得到更稀疏的投影矩阵,实验表明NCMF算法简单且有效。为了进一步提高分类精度,在算法中引入对特征词与类之间的模糊相关性测度,通过模糊相关系数计算文本到各类别的隶属度,并根据最大隶属度来确定文本的类别。通过从单个类及总体的分类准确度和执行时间等方面,与其他几种相关算法的比较实验结果表明NFC的总体性能优于其他算法,说明NFC是一种有效的网页文本分类算法。如何在词-文本及词-类别的模糊相关性分析中引入更丰富的语义信息,将是下一步的研究方向之一。此外,由于采用的测试数据集的规模还不是特别大,在对2个数据进行连乘时并未出现溢出这种极端情况,然而在处理海量数据时可能会出现溢出。针对在处理海量数据时,2个数据连乘可能出现的溢出问题进行研究也是一个很有意义的研究课题。
| [1] | Ozel S A. A web page classification system based on a genetic algorithm using tagged-terms as features[J]. Expert Systems with Applications, 2011, 38(4): 3407–3415. DOI:10.1016/j.eswa.2010.08.126 |
| [2] | Qi X, Davison B D. Web page classification:features and algorithms[J]. ACM Computing Surveys, 2009, 41(2): 10–12. |
| [3] | Kwon O W, Lee J H. Text categorization based on k-nearest neighbor approach for web site classification[J]. Information Processing and Management, 2003, 39(1): 25–44. DOI:10.1016/S0306-4573(02)00022-5 |
| [4] | Lin S S. A document classification and retrieval system for R & D in semi-conductor industry-a hybrid approach[J]. Expert Systems with Applications, 2009, 36(3): 4753–4764. DOI:10.1016/j.eswa.2008.06.024 |
| [5] | Yu B, Xu Z, LI C. Latent semantic analysis for text categorization using neural network[J]. Knowledge-Based Systems, 2008, 21(8): 900–904. DOI:10.1016/j.knosys.2008.03.045 |
| [6] | Li Y, Hung E, Chung K. A subspace decision cluster classifier for text classification[J]. Expert Systems with Applications, 2011, 38(10): 12475–12482. DOI:10.1016/j.eswa.2011.04.029 |
| [7] | Jiang S, Pang G, Wu M, et al. An improved K-nearest-neighbor algorithm for text categorization[J]. Expert Systems with Applications, 2012, 39(1): 1503–1509. DOI:10.1016/j.eswa.2011.08.040 |
| [8] | Ghiass M, Olschimke M, Moon B, et al. Automated text classification using a dynamic artificial neural network model[J]. Expert Systems with Application, 2012, 39(12): 10967–10976. DOI:10.1016/j.eswa.2012.03.027 |
| [9] | Chen J, Huang H, Tian S, et al. Feature selection for text classification with Naïve Bayes[J]. Expert Systems with Applications, 2009, 36(3): 5432–5435. DOI:10.1016/j.eswa.2008.06.054 |
| [10] | Lo S C. Web service quality control based on text mining using support vector machine[J]. Expert Systems with Applications, 2008, 34(1): 603–610. DOI:10.1016/j.eswa.2006.09.026 |
| [11] | Li C, Park S C. An efficient document classification model using an improved back propagation neural network and singular value decomposition[J]. Expert Systems with Applications, 2009, 36(2): 3208–3215. DOI:10.1016/j.eswa.2008.01.014 |
| [12] | Barman P C, Lee S Y. Document classification with unsupervised nonnegative matrix factorization and supervised percetron Learning[C]//Proceedings of the International Conference on Information Acquisition. Jeju City Korea:IEEE, 2007:2782-2785. |
| [13] | Lee J H, Park S, Ahn C M, et al. Automatic generic document summarization based on non-negative matrix factorization[J]. Information Processing and Management, 2009, 45(1): 20–34. DOI:10.1016/j.ipm.2008.06.002 |
| [14] | Zhu Z, Guo F, Zhu X, et al. Normalized dimensionality reduction using nonnegative matrix factorization[J]. Neurocomputing, 2010, 73(10-12): 1783–1893. DOI:10.1016/j.neucom.2009.11.046 |
| [15] | Yan J, Liu N, Zhang B, et al. OCFS:optimal orthogonal centroid feature selection for text categorization[C]//Proceedings of 28th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Salvador Brazil:Association for Computing Machinery, Inc., 2005:122-129. |
| [16] | Salton G, Buckley C. Term weighting approaches in automatic text retrieval[J]. Information Processing and Management, 1988, 24(5): 513–523. DOI:10.1016/0306-4573(88)90021-0 |
| [17] | Kim J. Toward faster nonnegative matrix factorization:a new algorithm and comparisons[C]//Proceedings of 8th IEEE International Conference on Data Mining, Pisa Italy:IEEE, 2008:353-362. |
| [18] |
张玉芳, 娄娟, 李智星, 等.
基于模糊关系的文本分类方法[J]. 计算机工程, 2011, 37(16): 149–151.
ZHANG Yufang, LOU Juan, LI Zhixing. Text classification approach based on fuzzy relationship[J]. Computer Engineering, 2011, 37(16): 149–151. DOI:10.3969/j.issn.1000-3428.2011.16.051 (in Chinese) |
| [19] | Lee C H, Yang H E, Ma S M. A novel multilingual text categorization system using latent semantic indexing[C]//Proceedings of the First International Conference on Innovative Computing, Information and Control, Beijing China:IEEE, 2006:503-506. |
| [20] |
徐燕, 李锦涛, 王斌, 等.
文本分类中特征选择的约束研究[J]. 计算机研究与发展, 2008, 45(4): 596–602.
XU Yan, LI Jingtao, Wang Bin, et al. A study on constraints for feature selection in text categorization[J]. Journal of Computer Research and Development, 2008, 45(4): 596–602. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

