2. 中国石油勘探开发研究院, 北京 100083;
3. 西安石油大学 科研处, 西安 710065
2. Research Institute of Petroleum Exploration and Development, Beijing 100083, China;
3. Scientific Research Department, Xi'an Shiyou University, Xi'an 710065, China
注水开发油藏、储层含水饱和度和井口含水率是评价油藏储量、油层水淹程度,进行油藏监测和管理的重要指标[1-4]。
含水饱和度获取方法主要有密闭取芯资料法[5-6]、地球物理测井法[7]、油藏数值模拟法和单井化学示踪剂法[8-11]。密闭取芯费用昂贵,且数据点有限;地球物理测井法通常采用经验关系式或者统计回归技术,通过测井信息来预测,计算精度和效果难以满足生产实践要求;油藏数值模拟工作量大,计算周期长;而单井化学示踪测试确定含水饱和度,是利用示踪剂在油层中的色谱分离原理,取决于示踪剂在平衡状态下的色谱效应,测试结果精度高,可成本也较高。
含水率预测方法目前主要有数值模拟法、经验公式法和解析法。含水率预测困难,受储层物性及流体等多因素影响[1, 12]。数值模拟方法是一种较好的预测方法,但需花费很多时间[13]。经验公式法只是对数据进行数学方法上的处理,缺乏具体物理意义,包括结合井的动、静态资料,利用神经网络法[14],应用Usher模型[15],Weibull预测模型、广义翁氏预测模型和瑞利预测模型[16]等建立含水率预测模型;利用水驱油实验数据拟合含水率变化曲线[17],建立含水率预测模型;基于实际聚合物驱含水率变化曲线的特征及定量表征模型的建立原则,建立含水率变化定量表征模型[18]。解析法包括基于分流量理论,结合相渗曲线预测含水率[19-22];1999年蒋明[23]、2007年Kazeem [3]和2011年Li等[2]对油藏做一定假设后,建立含水率与时间的数学关系模型;2010年许寒冰等[24]对注采井网内复势的研究和流线分布的刻画建立含水率解析解。这些方法均未考虑分层注水开发条件下油藏含水率的预测。
笔者应用井温曲线确定注水剖面,应用Poisson过程分析法,结合概率论方法,计算分层注水开发油藏任意时刻各小层中含水饱和度、见水时间和含水率。为油藏开发采取分层堵水措施等提供理论依据。
1 模型建立及求解 1.1 注水剖面确定分层注水开发油藏,可通过注水井的温度剖面,依据注入水、储层岩石的传质传热基本方程,确定注水剖面,即确定每一小层的注水量[25-26]。井眼质量和热量传递示意图见图 1。
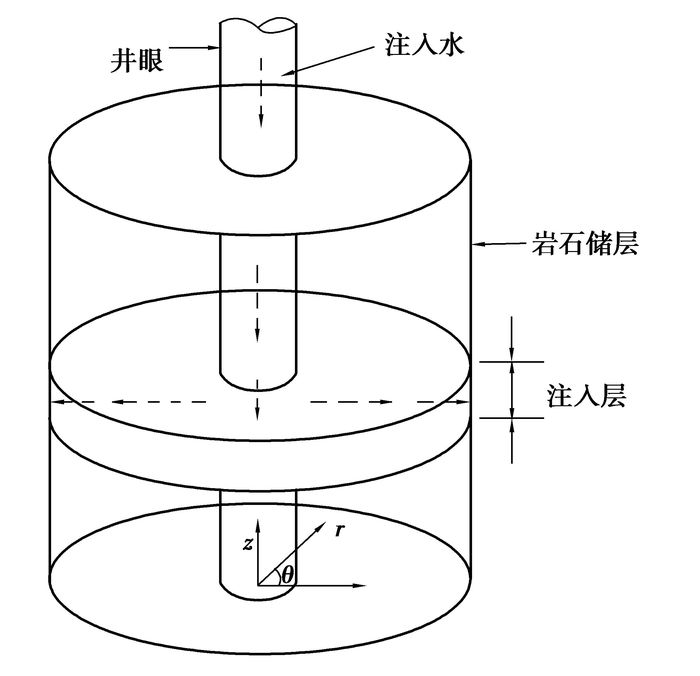
|
图 1 井眼质量和热量传递示意图 |
1) 水相传质传热方程。
井眼中水温变化:
| $ \begin{array}{l} {\rho _{\rm{w}}}{C_{\rm{w}}}\frac{{\partial {T_{\rm{w}}}}}{{\partial t}} = {\rho _{\rm{w}}}{C_{\rm{w}}}v\frac{{\partial {T_{\rm{w}}}}}{{\partial z}} + {k_{\rm{w}}}\frac{{{\partial ^2}{T_{\rm{w}}}}}{{\partial {z^2}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{2h}}{{{r_{\rm{w}}}}}\left[ {\left( {{r_{\rm{w}}},z,t} \right) - {T_{\rm{w}}}\left( {z,t} \right)} \right]。\end{array} $ | (1) |
初始条件:
| $ {T_{\rm{w}}}\left( {z,0} \right) = a + bz, $ | (2) |
边界条件:
| ${T_{\rm{w}}}\left( {{z_{\max }},t} \right) = {T_{\rm{s}}}\left( t \right),0 < t \le {t_{si}};$ | (3) |
| $ {k_{\rm{w}}}\frac{{\partial {T_{\rm{w}}}\left( {{z_{\max }},t} \right)}}{{\partial z}} = 0,{t_{si}} \le t; $ | (4) |
| $ {k_{\rm{w}}}\frac{{\partial {T_{\rm{w}}}\left( {0,t} \right)}}{{\partial z}} = 0,0 < t。$ | (5) |
其中:
| $ h = \alpha {\left[ {T\left( {{r_{{\rm{in}}}},z,t} \right) - {T_{\rm{w}}}\left( {z,t} \right)} \right]^{\frac{1}{4}}}。$ |
方程(1)是描述井眼中水相流量与温度变化的方程。当对流项
2) 岩层传质传热方程。
储层温度变化:
| $ \begin{array}{l} {\rho _{\rm{e}}}{C_{\rm{e}}}\frac{{\partial T}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{k_{fe}}\frac{{\partial T}}{{\partial r}}} \right) + \frac{\partial }{{\partial z}}\left( {{k_{fe}}\frac{{\partial T}}{{\partial z}}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{q_{\rm{w}}}{\rho _{\rm{w}}}{C_{\rm{w}}}}}{{2{\rm{ \mathsf{ π} }}r}}\frac{{\partial T}}{{\partial r}} + \frac{{{q_{\rm{w}}}\left( {{p_{\rm{w}}} - {p_{\rm{e}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{r^2}{J_c}\ln \left( {{r_{\rm{e}}}/{r_{\rm{w}}}} \right)}}。\end{array} $ | (6) |
初始条件:
| $ T\left( {r,z,0} \right) = a + bz, $ | (7) |
边界条件:
| $ T\left( {{r_{\rm{e}}},z,t} \right) = a + bz, $ | (8) |
| $ T\left( {r,0,t} \right) = a, $ | (9) |
| $ T\left( {r,{z_{\max }},t} \right) = a + b{z_{\max }}。$ | (10) |
其中:
方程(6)是描述井眼周围储层岩石的热量平衡,其适用于注水时的注水层;当径向对流
结合水相和岩层初始条件和边界条件,联立式(1)和式(6),就可通过有限差分计算出任意时刻各小层注水量qw (1,j,t)。具体求解过程:先给定注水剖面qw(1,j,t)的数值量,通过模型求出T1,jt数值解,然后分析T1,jt数值解和井温T1,jt测量值之间的差别,逐步调整注水剖面qw (1,j,t)的数值量,使T1,jt数值解逼近测量值,这时注水剖面qw (1,j,t)的数值量就可认为t时刻各小层的实际注水量。其中qw (1,j,t)为第t时刻径向第1网格纵向第j网格注水量,m3/d;T1,jt为第t时刻径向第1网格纵向第j网格井温,℃。
1.2 水流线速度推导注水开发油藏,注入水在储层中的推进速度与孔隙结构密切相关。以岩心做注水驱油实验,如图 2,岩心孔隙度为φ,横截面为A,单位时间注水量为Q,压力梯度为dp/dl,单位时间内水淹岩心体积为Q/φ,则水在岩心中推进速度为Q/(Aφ)。

|
图 2 注水驱油实验岩心 |
设岩心孔隙直径分为N级:γ1,γ2,…,γN,所占比例分别为p(γj)=pj,其中j=1,2,…,N;p1+p2+…+pN=1。假设平行于岩心轴线的任一直线穿过直径为γj的孔隙个数满足强度λj的Poisson过程[27],即假定岩心长为L,任一长度l:0≤l≤L,穿过直径为γj的孔隙个数为随机变量ζj(l),其概率分布为
| $ P\left( {{\zeta _j}\left( l \right) = k} \right) = \frac{{{{\left( {{\lambda _j}l} \right)}^k}}}{{k!}}{{\rm{e}}^{{\lambda _j}l}},k = 0,1, \cdots 。$ | (11) |
穿过长度l各级直径的孔隙总个数为随机变量
| $ \begin{array}{l} P\left( {\eta \left( l \right) = k} \right) = \frac{{{{\left( {\lambda l} \right)}^k}}}{{k!}}{{\rm{e}}^{\lambda l}} = \\ \frac{{{{\left[ {\left( {{\lambda _1} + {\lambda _2} + \cdots + {\lambda _N}} \right)l} \right]}^k}}}{{k!}}{{\rm{e}}^{\left( {{\lambda _1} + {\lambda _2} + \cdots + {\lambda _N}} \right)l}}。\end{array} $ | (12) |
强度参数λ为平行于岩心轴线的任一直线上单位距离所穿过的孔隙平均总个数,可通过岩心切片或电镜照片观测统计得到,也可通过数学推导方法确定。
| $ \tau = \frac{{{l_{孔}}}}{L} = \sqrt[3]{\varphi }, $ | (13) |
其中τ为线孔隙度,l孔为岩心长度L孔隙所占的总长度。
孔隙平均直径为
| $ \gamma = \sum\limits_{j = 1}^N {{\gamma _j}{P_j}} 。$ | (14) |
单位长度穿过孔隙的平均个数λ为
| $ \lambda = \frac{\tau }{\gamma } = \frac{{\sqrt[3]{\varphi }}}{\gamma }。$ | (15) |
水驱岩心实验中单位时间内水淹孔隙的平均个数为
| $ n = \lambda \cdot \frac{Q}{{A\varphi }}。$ | (16) |
这些孔隙所连成的平均距离为
| $ l = n \cdot \gamma = \frac{{\lambda Q\gamma }}{{A\varphi }}。$ | (17) |
则水在岩心推进的平均速度可表示成
| $ \bar \upsilon = \frac{{\frac{{\lambda Q\gamma }}{{A\varphi }}}}{{{\varphi ^{\frac{1}{3}}}}} = \frac{{\lambda Q\gamma }}{{A{\varphi ^{\frac{4}{3}}}}}。$ | (18) |
在实际油藏开发中,注入水沿各流线的推进速度并不都是υ,而是随机变量Uw。同样,水流线上单位时间内水淹孔隙的总个数也为随机变量,记为ζw,都服从Poisson分布,即
| $ P\left( {{\zeta _{\rm{w}}} = k} \right) = \frac{{{{\left[ {\frac{{\lambda Q}}{{A\varphi }}} \right]}^k}}}{{k!}}{{\rm{e}}^{\frac{{\lambda Q}}{{A\varphi }}}}。$ | (19) |
并且有
| $ {U_{\rm{w}}} = {\zeta _{\rm{w}}}\frac{\gamma }{{\sqrt[3]{\varphi }}}, $ | (20) |
| $ P\left( {{U_{\rm{w}}} = k\frac{\gamma }{{\sqrt[3]{\varphi }}}} \right) = \frac{{{{\left[ {\frac{{\lambda Q}}{{A\varphi }}} \right]}^k}}}{{k!}}{{\rm{e}}^{\frac{{\lambda Q}}{{A\varphi }}}}。$ | (21) |
式(21)描述岩心各处水推进速度的随机性速度,其平均速度为
| $ \begin{array}{l} {\rm{E}}\left( {{U_{\rm{w}}}} \right) = \sum\limits_{k = 0}^ \propto {k\frac{\gamma }{{\sqrt[3]{\varphi }}}P\left( {{U_{\rm{w}}} = k\frac{\gamma }{{\sqrt[3]{\varphi }}}} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{\gamma }{{\sqrt[3]{\varphi }}}\frac{{\lambda Q}}{{A\varphi }} = \frac{{\lambda Q\gamma }}{{A{\varphi ^{\frac{4}{3}}}}} = \frac{Q}{{A\varphi }}。\end{array} $ | (22) |
这与实验中水在岩心中宏观推进速度Q/(Aφ)的推导结果是一致的。
对应方差为
| $ {\rm{D}}\left( {{U_{\rm{w}}}} \right) = \frac{{{\gamma ^2}}}{{{\varphi ^{\frac{2}{3}}}}}\frac{{\lambda Q}}{{A\varphi }} = \frac{{\lambda Q{\gamma ^2}}}{{A{\varphi ^{\frac{5}{3}}}}}。$ | (23) |
假设任一平行于岩心轴线的直线l所穿过的孔隙总个数及其单侧的岩石骨架的长度之和为随机变量Y,其数学期望和方差分别为E(Y)、D(Y),以Yi表流线上第i个孔隙与其一侧的岩石骨架长度之和,Yi与Y相互独立且相同分布,则水淹速度Uw可表示为
| $ {U_{\rm{w}}} = \sum\limits_{i = 1}^{\left[ {\frac{{\lambda Q}}{{A\varphi }}} \right]} {{Y_i}} 。$ | (24) |
Uw均值为
| $ {\rm{E}}\left( {{U_{\rm{w}}}} \right) = \frac{{\lambda Q}}{{A\varphi }}{\rm{E}}\left( Y \right)。$ | (25) |
对应方差为
| $ {\rm{D}}\left( {{U_{\rm{w}}}} \right) = \frac{{\lambda Q}}{{A\varphi }}{\rm{D}}\left( Y \right)。$ | (26) |
对任一时间段t内的水淹距离
| $ U\left( t \right) = \sum\limits_{i = 1}^{\left[ {\frac{{\lambda Q}}{{A\varphi }}t} \right]} {{Y_i}} , $ | (27) |
这里
则U(t)均值为
| $ {\rm{E}}\left[ {U\left( t \right)} \right] = \frac{{\lambda Q}}{{A\varphi }} \cdot t \cdot {\rm{E}}\left( Y \right)。$ | (28) |
对应方差为
| $ {\rm{D}}\left[ {U\left( t \right)} \right] = \frac{{\lambda Q}}{{A\varphi }} \cdot t \cdot {\rm{D}}\left( Y \right)。$ | (29) |
假设某油藏以五点法注采井网开采,储层中水从注入井到生产井推进过程如图 3,设A为注入井,B为生产井,建立坐标系0~x~y。由对称性,仅分析正方形对角线OB下方的三角形区域。
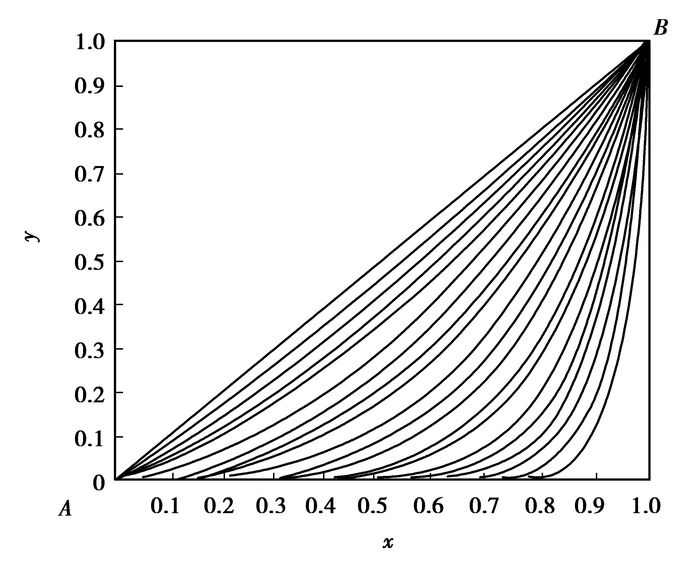
|
图 3 五点法注采井网水流线示意图 |
式(30)函数族的曲线与按等产量—源—汇的流线方程(31)
| $ y = {x^\alpha },\left( {0 \le x \le 1,参变量\;\alpha \ge 1} \right), $ | (30) |
| $ {\rm{arctg}}\frac{y}{{x - a}} - {\rm{arctg}}\frac{y}{{x + a}} = c\left( {c\;常数} \right) $ | (31) |
的流线非常接近,因此将三角形区域内的流线近似地以函数y=xα表示。当α=1,是正方形对角线,长为
| $ {l_\alpha } = \int_0^1 {\sqrt {1 + {{\left[ {\frac{{{\rm{d}}{x^\alpha }}}{{{\rm{d}}x}}} \right]}^2}} {\rm{d}}x} = \int_0^1 {\sqrt {1 + {\alpha ^2}{x^{2\left( {\alpha - 1} \right)}}} {\rm{d}}x} 。$ | (32) |
适当选取一组α值α1>α2>…>αn,则可绘出n条流线
| $ y = {x^{{\alpha _i}}},i = 1,2, \cdots ,n。$ | (33) |
当注入井压力Pe和生产井井底流压Pw都稳定时,注入水沿长度为lα流线的压力梯度为
| $ {\rm{grad}}{P_\alpha } = \frac{{{P_{\rm{e}}} - {P_{\rm{w}}}}}{{{l_\alpha }}}。$ | (34) |
结合达西定律
| $ Q = A\frac{K}{\mu }{\rm{grad}}P, $ | (35) |
将式(35)代入式(28),则经时间t水淹推进平均距离为
| $ {\rm{E}}\left[ {U\left( t \right)} \right] = \frac{{\lambda Kt}}{{\mu \varphi }}{\rm{E}}\left( Y \right) \cdot {\rm{grad}}P。$ | (36) |
同理,水淹推进距离的方差为
| $ {\rm{D}}\left[ {U\left( t \right)} \right] = \frac{{\lambda Kt}}{{\mu \varphi }}{\rm{D}}\left( Y \right) \cdot {\rm{grad}}P。$ | (37) |
根据式(36)和(37)可计算出任意时刻不同流线的水淹推进距离和对应方差,据此得到t时的各流线水淹前缘位置,依次连接各流线水淹前缘位置就可画出t时油水界面曲线,此油水界面曲线包围的面积与总面积之比就是t时储层含水饱和度。
1.4 含水率计算对于同一小层,根据达西定律,流量与压力梯度成正比,将各流线压力梯度累积求总和ΔPk,记为
| $ \Delta {P_k} = \sum\limits_{i = 1}^{{n_k}} {{\rm{grad}}{P_k}{\alpha _i}} , $ | (38) |
其中k为层号,nk为第k层流线的总条数,gradPkαi为第αi条流线的总压降。
假设在t时刻共有n(t)条流线水驱前缘已到达生产井,此时这些流线已全部为水相,将这些流线上压力梯度累积求和为
| $ \Delta {P_{k水}} = \sum\limits_{i = 1}^{{n_k}\left( t \right)} {{\rm{grad}}{P_k}{\alpha _i}} 。$ | (39) |
则此时第k小层含水率fkw(t)为
| $ {f_{k{\rm{w}}}}\left( t \right) = 100\% \cdot \frac{{\Delta {P_{k水}}}}{{\Delta {P_k}}}。$ | (40) |
将各小层含水率与对应产量加权平均,得到t时刻的生产井含水率fw(t)为
| $ {f_{\rm{w}}}\left( t \right) = \frac{{\sum\limits_{i = 1}^k {{q_k} \cdot {f_{k{\rm{w}}}}\left( t \right)} }}{{{Q_{\rm{L}}}}}, $ | (41) |
其中qk为第k层产液量,QL为生产井总产液量。
2 模型应用某注水开发油藏,井深3 980 m,控制半径88 m,原始地层压力Pi=40.8 MPa,生产井中程深度压力为32 MPa,套管压力43.2 MPa,套管直径14.6 cm,井距200 m采用五点法注采井网,注入压力Pe=45 MPa,日注水量150 m3,注入时间5 610 h,注入水温度18.5 ℃,注水层面:L1为3 562.3~3 609.6 m,L2为3 609.6~3 668.1 m,L3为3 668.1~3 726.6 m,L4为3 726.6~3 785.2 m,L5为3 785.2~3 852.2 m,注入水的黏度μw=1 m·Pa·s,油的黏度μo=1.5 m·Pa·s,原始含油饱和度Soi=0.7,储层平均孔隙度φ=11.25%,渗透率K=32.51×10-3 μm3。储层孔隙体系分布如表 1。
| 表 1 储层孔隙体系分布 |
依据1.1小节,基于水相和岩石的传质传热方程,给定一初始注水剖面,通过有限差分求解方法,求取井温剖面数值解,通过调整注水井的注水剖面,使得井温剖面数值解接近实测值,最终确定了注水剖面,结果见图 4。
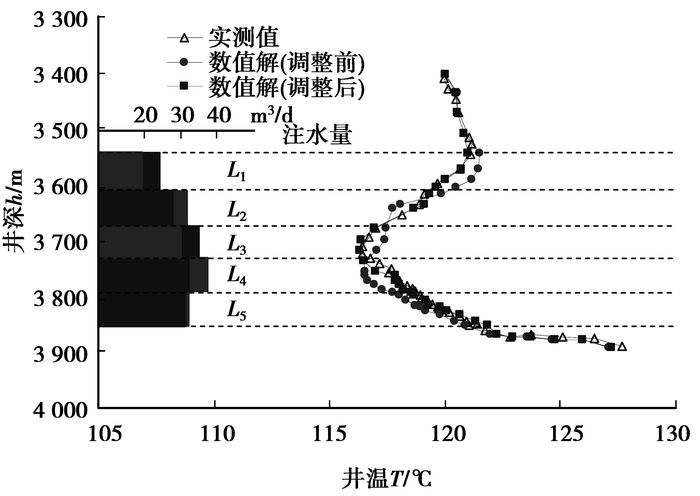
|
图 4 注水井的井温剖面及注水剖面 |
注水井总共分5小层注水,各层注水量分别为Q1=24 m3,Q2=28 m3,Q3=35 m3,Q4=32 m3,Q5=31 m3。
2.2 含水饱和度基于1.1小节已确定各层注水量,根据1.2小节各层水流线速度推导,计算出任意时刻不同流线的水淹推进距离,据此就可画出任意时刻油水界面曲线,从而得到任意时刻各层含水饱和度,见图 5~7。
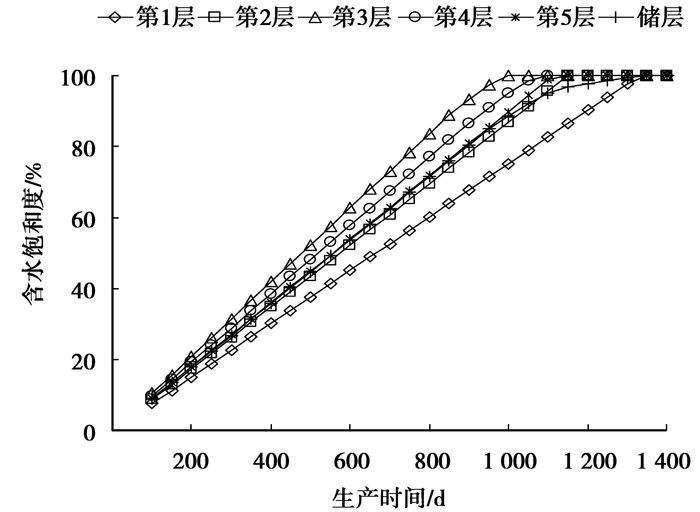
|
图 5 各层含水饱和度变化曲线 |
|
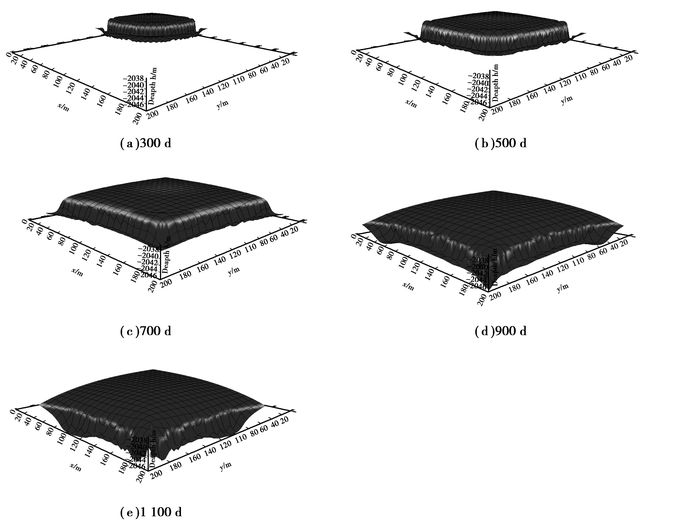
图 6 第1层油水界面变化 |
|
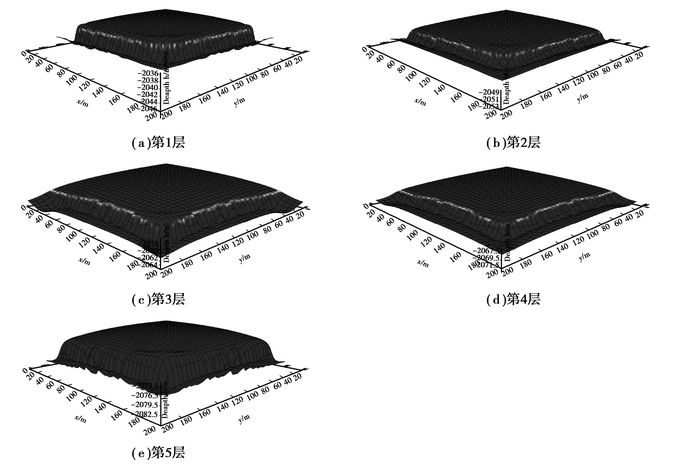
图 7 第600 d各层油水界面 |
从图 5可知,含水饱和度上升最快的是第3层,其注水强度最大为0.648 m3/(d·m),其次为第4层,上升最慢的是第1层,注水强度也最小,为0.508 m3/(d·m)。
从图 6可知,随注水开发进行,第1小层油水界面不断扩展,到了第1 100 d水已在生产井发生突破。
从图 7可知,在第600 d,第3层油水界面推进最快,第1层油水界面推进最慢,与图 6结果一致。
2.3 含水率基于以上计算结果,根据1.4小节,可计算各层的见水时间及任意时刻的含水率,见图 8~10。
|
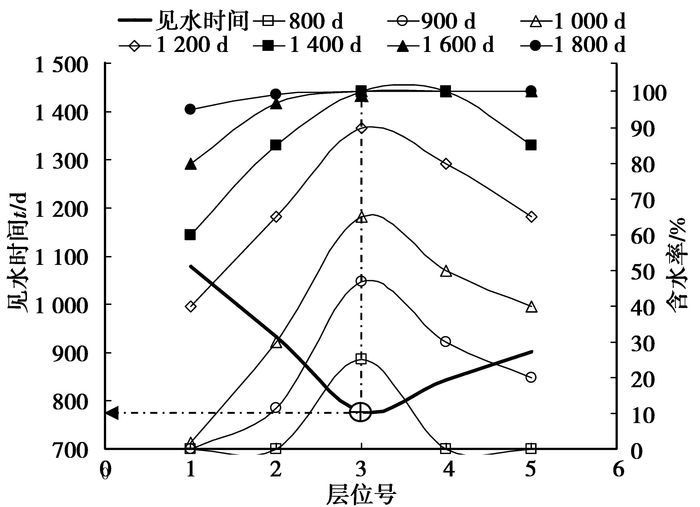
图 8 各层见水时间及含水率变化 |
|
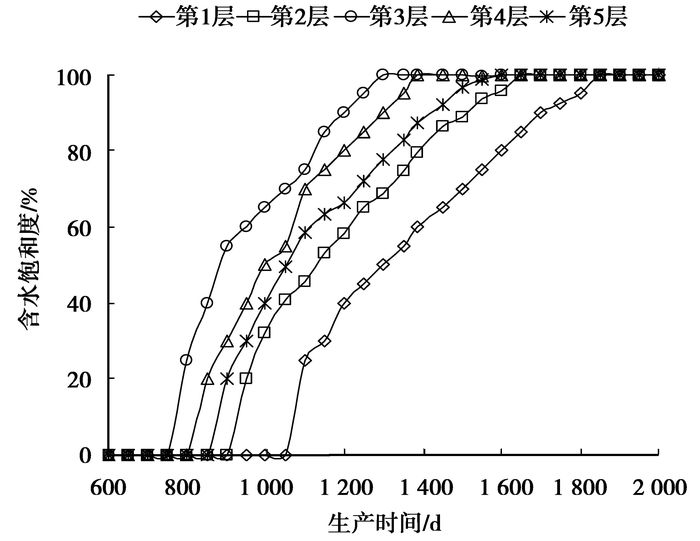
图 9 各层含水率变化 |
|
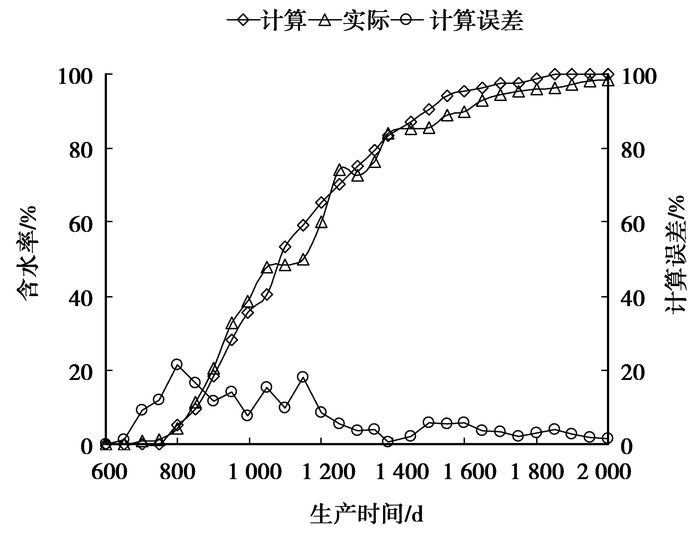
图 10 生产井含水率计算误差 |
见水最早的是第3层,为779 d,其含水上升率最快;其次是第4层为884 d,最晚见水为第1层,1 078 d,其含水上升率最慢。1 600 d之后,各层含水率都高达80%以上,趋于一致。
见水之后,各层含水率在初期上升较快,之后慢慢减缓。第3层含水率上升起始时刻早,上升快,第1 250 d含水率为98.5%,水淹严重;第1层含水率上升起始时刻晚,上升慢,第1 850 d含水率为99.1%,几乎全部水淹。
按每小层产液量加权平均,计算得到生产井的含水率,将其与井口计量的含水率进行对比,见图 10。初期计算误差较大,后期较小,在5%之内。这是由于见水初期,水量大部分来自裂缝等高渗透通道,建立模型未考虑此影响,当常规层位逐渐见水后,此影响削弱,计算的含水率更接近实际,误差小。
3 结论1) 建立了分层注水开发油藏水淹动态跟踪模型。基于传质传热原理,根据井温曲线确定注水剖面,应用Poisson过程分析法,结合概率论方法,计算注水开发油藏任一时刻各小层中含水饱和度、见水时间和含水率。
2) 分层注水开发油藏,各小层水淹动态过程不同。注水强度大,存在裂缝等高渗透通道的小层,含水饱和度增大快,见水时间早,且含水率上升快,反之。
3) 在不同开发时期,模型预测精度不同。由于模型考虑了储层的微观孔隙分布,但未考虑微裂缝等高渗透通道,故在见水初期,水主要来自高渗透通道时,计算含水率误差较大,随着常规储层逐步水淹,计算含水率越趋于实测含水率,计算误差小于5%。
| [1] |
郭元岭, 苏国英.
水淹油层含水率解释精度影响因素分析[J]. 石油勘探与开发, 1998, 25(4): 59–61.
GUO Yuanling, SUN Guoying. An analysis of factors affecting the precision of log interpretation of water cut in a watered out reservoir[J]. Petroleum Exploration and Development, 1998, 25(4): 59–61. (in Chinese) |
| [2] | Li K W, Ren X H, Li L, et al. A new model for predicting water cut in oil reservoirs[C]//Proceedings of the EAGE Annual Conference and Exhibition, May 23-26, 2011, Vienna, Austria.[S.l.]:SPE, 2011:143481. |
| [3] | Kazeem A, Langaas K. A didactic analysis of water cut trend during exponential oil-decline[C]//Proceedings of the Nigeria Annual International Conference and Exhibition, August 6-8, 2007, Abuja, Nigeria.[S.l.]:SPE, 2007:111920. |
| [4] |
杨斌, 匡立春, 孙中春, 等.
基于遗传规划的储层含水饱和度预测方法[J]. 成都理工大学学报:自然科学版, 2006, 33(2): 209–213.
YANG Bin, KUANG Lichun, SUN Zhongchun, et al. Prediction of reservoir water saturation by genetic programming[J]. Journal of Chengdu University of Technology:Science & Technology Edition, 2006, 33(2): 209–213. (in Chinese) |
| [5] |
王敏, 孙建孟, 赖富强, 等.
低闭合油藏油水同层储层含水饱和度新模型[J]. 西南石油大学学报:自然科学版, 2010, 32(1): 27–32.
WANG Min, SUN Jianmeng, LAI Fuqiang, et al. A new water saturation model for non-net pay in low closure reservoir[J]. Journal of Southwest Petroleum University:Science & Technology Edition, 2010, 32(1): 27–32. (in Chinese) |
| [6] |
郭元岭, 鲁国明.
水淹层含水率与含水饱和度的区域性直线模型及应用[J]. 油气采收率技术, 1996, 3(2): 45–49.
GUO Yuanling, LU Guoming. Regional linear model of water cut vs. water saturation in watered-out zone and its application[J]. Oil & Gas Recovery Technology, 1996, 3(2): 45–49. (in Chinese) |
| [7] |
贺国芬, 袁洪林, 路涛, 等.
一种同时反演地层水电阻率和含水饱和度的方法[J]. 国外测井技术, 2010(1): 37–39, 42.
HE Guofen, YUAN Honglin, LU Tao, et al. An inversion method to determine formation water resistivity and water saturations simultaneously[J]. World Well Logging Technology, 2010(1): 37–39, 42. (in Chinese) |
| [8] | Deans H A. Method of determining fluid saturations in reservoirs:US, 3623842[P]. 1971-11-30. |
| [9] | Deans H A, Shallenberger L K. Single-well chemical tracer method to measure connate water saturation[C]// Proceedings of the SPE Improved Oil Recovery Symposium, April 22-24, 1974, Tulsa, Oklahoma. [S.l.]:SPE, 1974:4755. |
| [10] | Deans H A, Mut A D. Chemical tracer studies to determine water saturation at Prudhoe Bay[J]. SPE Reservoir Engineering, 1997, 12(1): 52–57. DOI:10.2118/28591-PA |
| [11] | Ccockin A P, Malcolm L T, McGuire P L, et al. Analysis of a single-well chemical tracer test to measure the residual oil saturation to a hydrocarbon miscible gas flood at Prudhoe Bay[J]. SPE Reservoir Evaluation & Engineering, 2000, 3(6): 544–551. |
| [12] |
屈亚光, 刘月田, 胥小伟.
高尚堡多层系复杂断块油藏含水率变化影响因素研究[J]. 石油天然气学报, 2010, 32(2): 120–124.
QU Yaguang, LIU Yuetian, XU Xiaowei. Influential factors of water-cut variation in multi-layer and complicated fault-block reservoirs in Gaoshangbao Oilfield[J]. Journal of Oil and Gas Technology, 2010, 32(2): 120–124. (in Chinese) |
| [13] |
赵国忠, 孟曙光, 姜祥成.
聚合物驱含水率的神经网络预测方法[J]. 石油学报, 2004, 25(1): 70–73.
ZHAO Guozhong, MENG Shuguang, JIANG Xiangcheng. Neural network method for prediction of water cut in polymer flooding[J]. Acta Petrolei Sinica, 2004, 25(1): 70–73. DOI:10.7623/syxb200401015 (in Chinese) |
| [14] |
唐洪, 罗明高.
利用神经网络预测不同开发期生产井的含水率[J]. 西南石油学院学报, 2003, 25(3): 30–32.
TANG Hong, LUO Minggao. The study of the water-cut of the development wells during the different period[J]. Journal of Southwest Petroleum Institute, 2003, 25(3): 30–32. (in Chinese) |
| [15] |
杨希军.
应用Usher模型预测单井含水率变化[J]. 西安石油大学学报:自然科学版, 2008, 23(3): 50–51.
YANG Xijun. Prediction of the variation of single-well water-cut using Usher model[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2008, 23(3): 50–51. (in Chinese) |
| [16] |
刘朝霞, 韩冬, 王强, 等.
一种预测聚合物驱含水率的新模型[J]. 石油学报, 2009, 30(6): 903–907.
LIU Zhaoxia, HAN Dong, WANG Qiang, et al. A new model for water-cut prediction in polymer flooding[J]. Acta Petrolei Sinica, 2009, 30(6): 903–907. DOI:10.7623/syxb200906019 (in Chinese) |
| [17] |
刘金玉, 王殿生, 刘柏林, 等.
低渗低饱和砂岩水驱油过程中含水率变化规律研究[J]. 西安石油大学学报:自然科学版, 2011, 26(1): 37–41.
LIU Jinyu, WANG Diansheng, LIU Bolin, et al. Study on the variation law of the water-cut of low-permeability low-saturation sandstone reservoirs in water displacing oil[J]. Journal of Xi'an Shiyou University:Natural Science Edition, 2011, 26(1): 37–41. (in Chinese) |
| [18] |
赵辉, 李阳, 曹琳.
聚合物驱含水率变化定量表征模型[J]. 石油勘探与开发, 2010, 37(6): 737–742.
ZHAO Hui, LI Yang, CAO Lin. A quantitative mathematic model for polymer flooding water-cut variation[J]. Petroleum Exploration and Development, 2010, 37(6): 737–742. (in Chinese) |
| [19] | Ershaghi I, Omorigie O. A method for extrapolation of cut vs recovery curves[J]. Journal of Petroleum Technology, 1978, 30(2): 203–204. DOI:10.2118/6977-PA |
| [20] | Sitorus J, Sofyan A, Abdulfatah M Y. Developing a fractional flow curve from historic production to predict performance of new horizontal wells, Bekasap Field, Indonesia[C]//Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, September 11-13, 2006, Adelaide, Australia.[S.l.]:SPE, 2006:101144. |
| [21] | Lo K K, Warner H R, Johnson J B. A study of the post-breakthrough characteristics of waterfloods[C]//Proceedings of SPE California Regional Meeting, April 4-6, 1990, Ventura, California.[S.l.]:SPE, 1990:20064. |
| [22] | Ershaghi I, Abdassah D. A prediction technique for immiscible processes using field performance data[J]. Journal of Petroleum Technology, 1984, 36(4): 664–670. DOI:10.2118/10068-PA |
| [23] |
蒋明, 宋富霞, 吴行才.
含水率与时间关系数学模型的建立及应用[J]. 石油勘探与开发, 1999, 26(1): 65–67.
JIANG Ming, SONG Fuxia, WU Xingcai. Building and application of a mathematical model for water cut and time relationship[J]. Petroleum Exploration and Development, 1999, 26(1): 65–67. (in Chinese) |
| [24] |
许寒冰, 李相方, 石德佩, 等.
注采井网生产井含水率解析计算方法[J]. 石油学报, 2010, 31(3): 471–474.
XU Hanbing, LI Xiangfang, SHI Depei, et al. An analytical method for calculating water cut of producers in injection-production pattern[J]. Acta Petrolei Sinica, 2010, 31(3): 471–474. DOI:10.7623/syxb201003022 (in Chinese) |
| [25] | Li H, Zhu D, Lake L W, et al. A new method to interpret two-phase profiles from temperature and flow meter logs[C]//Proceedings of the SPE Annual Technical Conference and Exhibition, October 3-6, 1999, Houston, Texas.[S.l.]:SPE, 1999:56793. |
| [26] | John F, Scott F H, Brent D C, et al. An improved simulation for interpreting temperature logs in water injection wells[J]. SPE Journal, 1982, 22(5): 709–718. DOI:10.2118/10081-PA |
| [27] |
姚恒申, 向开理, 李治平.
油藏含水饱和度的泊松过程分析方法[J]. 系统工程理论与实践, 1999(3): 137–142.
YAO Hengshen, XIANG Kaili, LI Zhiping. Analytical forecasting for water saturation of reservoirs[J]. Systems Engineering-Theory & Practice, 1999(3): 137–142. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


