2. 北京理工大学 机械与车辆学院, 北京 100081
2. School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China
人类社会可持续发展对汽车技术提出了更高的环保和节能要求,而混合动力汽车因为具有良好的性价比,成为目前得到广泛应用的清洁能源汽车,其中ISG(Integrated Starter Generator)型混合动力汽车中,ISG电机取代了发动机的启动电机和发电机,直接与发动机的曲轴相连,实现动力的耦合,系统结构简单,只有一个电机,成本相对较低,是混合动力系统中重要的结构形式[1-2]。传统的ISG电机混合动力系统中,由于发动机的反拖,不能有效回收制动能量,也不具备通过电机调整发动机工作点的功能,因此在常规ISG混合动力系统的基础上,人们开展了ISG速度耦合混合动力系统的研究。
由于在混合动力系统中有多个动力源,为此对系统能量的优化管理是提高系统性能的重要方式,在目前混合动力汽车的能量管理控制策略中,主要有以下几类控制策略:基于规则的控制策略、局部最优控制策略和全局最优控制策略。
基于规则的控制策略,主要依靠工程经验设定门限或控制规则,是将发动机和电机的工作区域限制在一定高效工作区域内的控制策略[3-5]。但无论门限还是规则,都具有定性模糊的特点,由于工况或参数的变化,系统无法实现优化的控制。瞬时优化控制策略[6-8]通过实时计算发动机和电动机在不同功率分配组合和不同工作点处的瞬时燃油消耗和排放最优,以确定最佳的混合动力系统工作模式和工作点。其中最具发展前景的是Paganelli等[9]提出的等效燃油最小控制策略。但其计算量较大且结果只能得到局部最优解。全局优化是指在已知工况前提下,以整个工况内整车的总燃油消耗量最小等为目标进行优化的方法。在已知工况条件下,全局最优控制的整车燃油经济性优于瞬时最优控制。全局最优控制一般采用模拟退火[10]和动态规划[11-14]等优化算法。采用动态规划的全局最优化控制策略,可以得出在已知工况下混合动力系统的最佳能量管理策略,也为进一步混合动力系统实用化控制策略的拟定和系统参数的设计奠定了基础。
但上述研究大部分都是以提高燃油经济性为目标,忽略了电池荷电状态的管理和频繁换挡带来的影响。利用动态规划方法,针对ISG型速度耦合混合动力汽车的具体特点,建立了全局优化控制策略,在有效降低油耗的同时保证了SOC的平衡和减少了频繁换挡,为评价其他控制策略提供了参考,为提炼出实时控制规则奠定了基础。
1 ISG型混合动力传动系统模型一种ISG速度耦合混合动力传动系统的结构如图 1所示。该混合动力传动系统中采用行星排进行速度耦合,发动机接齿圈,ISG电机接太阳轮,动力通过行星架输出,电机和发动机之间有单向离合器和湿式多片离合器。
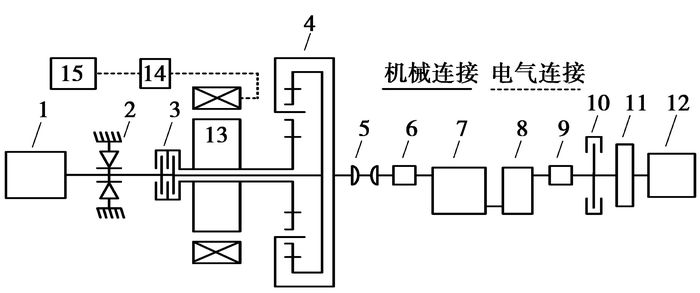
|
图 1 混合动力系统的结构图 1.发动机;2.单向离合器;3.湿式多片离合器;4.行星排;5.十字万向节;6.HBM200转速转矩传感器;7.AMT变速器;8.升速箱;9.HBM1000转速转矩传感器;10.制动器;11.惯性飞轮;12.电涡流测功机;13.ISG电机;14.功率转换器;15.蓄电池组 |
该混合动力传动系统,通过离合器的结合、分离以及对ISG电机的控制,能实现多种工作模式,如表 1所示。当系统纯电动驱动时,离合器断开,由于有单向离合器作用,发动机不能反向运动被制动,ISG电机通过行星传动装置输出动力,此外再生制动也可以在没有发动机反拖转矩的影响下回收能量;在行进中启动发动机时,结合湿式多片离合器,当离合器结合时,系统是常规的ISG混合动力系统,当脱开湿式多片离合器时,还可以利用行星轮系的速度耦合作用进行无级调速,调节发动机工作点。本系统在保持ISG结构简单和良好性价比的基础上,进一步提升了传动系统的性能。因此本系统相对常规ISG混合动力系统是一种性能改良的混合动力传动。
| 表 1 ISG型速度耦合混合动力汽车工作模式 |
为了研究发动机和电机动力传动的能量分配优化策略,必须建立传动系统的动力学模型,对图 1所示结构进行动力学分析,得到如图 2所示的动力学模型。
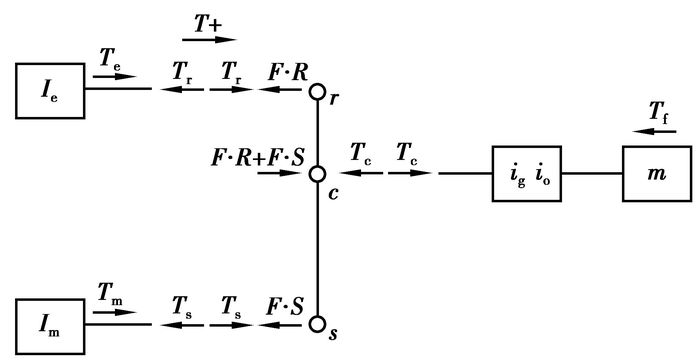
|
图 2 混合动力系统力学模型图 |
选择动力传动向右为正方向,以发动机和齿圈为研究对象,发动机与行星轮系的齿圈连接,发动机的惯量为Ie,输出扭矩为Te,齿圈的惯量为Ir,齿圈传来给发动机的阻力矩为F·R,其动力学方程为
| $ \left( {{I_{\rm{e}}} + {I_{\rm{r}}}} \right){{\dot \omega }_{\rm{e}}} = {T_{\rm{e}}} - F \cdot R。$ | (1) |
以ISG电机和太阳轮为研究对象,ISG电机与行星轮系的太阳轮连接,电机的惯量为Im,输出扭矩为Tm,太阳轮的惯量为Is,太阳轮传给电机的阻力矩为F·S,其动力学方程为
| $ \left( {{I_{\rm{m}}} + {I_{\rm{s}}}} \right){{\dot \omega }_{\rm{m}}} = {T_{\rm{m}}} - F \cdot S。$ | (2) |
系统动力通过行星轮系的行星架输出,行星架的转动惯量为Ic,由行星轮系的力矩平衡,结合公式(1)和(2),发动机和电机转换到行星架上的驱动扭矩为F(R+S),则考虑到整车阻力矩和以整车质量折算到行星架处的等效惯量,其动力学方程为
| $ \left( {{I_{\rm{c}}} + \frac{{R_{\rm{w}}^2}}{{i_{\rm{g}}^2i_o^2}}m} \right){{\dot \omega }_o} = F\left( {R + S} \right) - {T_{\rm{f}}}。$ | (3) |
根据行星轮系的转速关系,有以下公式成立:
| $ \left. \begin{array}{l} {\omega _{\rm{s}}}S + {\omega _{\rm{r}}}R - \left( {R + S} \right){\omega _{\rm{c}}} = 0,\\ {{\dot \omega }_{\rm{s}}}S + {{\dot \omega }_{\rm{r}}}R - \left( {R + S} \right){{\dot \omega }_{\rm{c}}} = 0,\\ {{\dot \omega }_{\rm{m}}}S + {{\dot \omega }_{\rm{e}}}R - \left( {R + S} \right){{\dot \omega }_o} = 0。\end{array} \right\} $ | (4) |
式中Ie、Im、Ir、Is、Ic分别为发动机、ISG电机、行星排齿圈、行星排太阳轮和行星架的转动惯量,kg·m2;ωs、ωr、ωc分别为行星排太阳轮、行星排齿圈和行星排行星架转速,rad/s;ωe、ωm、ωo分别为发动机、ISG电机和输出转速,rad/s;F为行星齿轮啮合力的切向分力,N;R、S分别为行星排齿圈和太阳轮的节圆半径,m;Te、Tm、Tf分别为发动机转矩、电机转矩和行驶阻力矩,N·m;Rw为车轮半径,m;m为整备质量,kg;g为重力加速度,m/s2;α为爬坡坡度;f为滚动阻力系数;CD为空气阻力系数;A为迎风面积,m2;u为汽车行驶车速,m/s;δ为汽车旋转质量换算系数;ig为AMT传动比;io为主减速器传动比。
联立上述公式,得到如下的关系矩阵:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{I_{\rm{e}}} + {I_{\rm{r}}}}&0&0&R\\ 0&{{I_{\rm{c}}} + \frac{{R_{\rm{w}}^2}}{{i_{\rm{g}}^2i_o^2}}m}&0&{ - \left( {R + S} \right)}\\ 0&0&{{I_{\rm{m}}} + {I_{\rm{s}}}}&S\\ R&{ - \left( {R + S} \right)}&S&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot \omega }_{\rm{e}}}}\\ {{{\dot \omega }_o}}\\ {{{\dot \omega }_{\rm{m}}}}\\ F \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{T_{\rm{e}}}}\\ { - {T_{\rm{f}}}}\\ {{T_{\rm{m}}}}\\ 0 \end{array}} \right]。} \end{array} $ | (5) |
发动机工作时的单位油耗率方程[15]为
| $ Q = \frac{{{P_{\rm{e}}}b}}{{367.1\rho g}}, $ | (6) |
| $ {P_{\rm{e}}} = \frac{{{\rm{ \mathsf{ π} }}{T_{\rm{e}}}{n_{\rm{e}}}}}{{30}}, $ | (7) |
式中:Q为单位时间的油耗量,mL/s;Pe为发动机输出功率,kW;ρ为燃油密度,kg/L;b为当前转速转矩下的燃油消耗率,g/(kW·h-1)。
已知发动机转速和转矩,可在发动机油耗数值模型中插值得到b,发动机油耗数值模型如图 3所示。
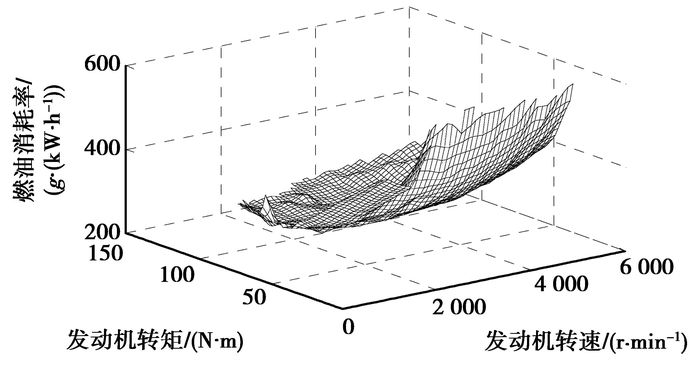
|
图 3 发动机油耗数值模型 |
ISG电机功率方程如下。
作电动机用时,所需功率
| $ {P_{\rm{m}}} = \frac{{{\rm{ \mathsf{ π} }}{T_{\rm{m}}}{n_{\rm{m}}}}}{{30{\eta _{\rm{m}}}}}。$ | (8) |
作发电机用时,发电功率
| $ {P_{\rm{m}}} = \frac{{{\rm{ \mathsf{ π} }}{T_{\rm{m}}}{n_{\rm{m}}}}}{{30}}{{\eta '}_{\rm{m}}}。$ | (9) |
式中:ηm为电机用作电动机时的效率;ηm′为电机用作发电机时的效率。
已知ISG电机转速和转矩,可在电机效率模型中插值得到效率。电机效率模型如图 4所示。
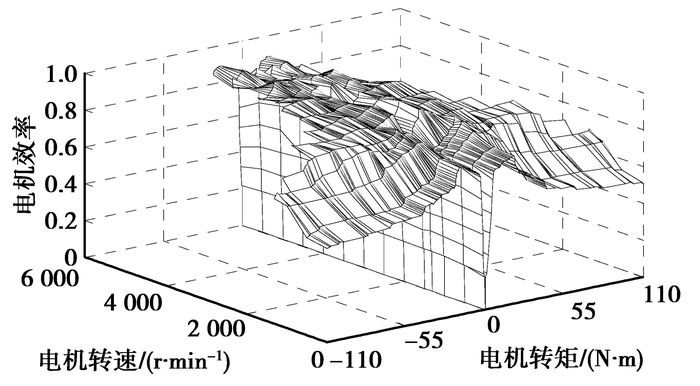
|
图 4 电机效率模型 |
电池组功率方程为
| $ {P_{\rm{b}}} = {U_{\rm{b}}} \times {I_{\rm{b}}}, $ | (10) |
式中,Pb为电池组输出功率,kW;Ib为回路电流,A;Ub为电池组端电压,V。
式(10)中,电池组的回路电流和端电压计算式为
| $ {U_{\rm{b}}} = {E_{\rm{b}}}\left( {{\rm{SOC}}} \right) - {R_{\rm{b}}}\left( {{\rm{SOC}}} \right) \times {I_{\rm{b}}}, $ | (11) |
| $ {I_{\rm{b}}} = \frac{{{E_{\rm{b}}}\left( {{\rm{SOC}}} \right) - \sqrt {E_{\rm{b}}^2\left( {{\rm{SOC}}} \right) - 4 \times {R_{\rm{b}}}\left( {{\rm{SOC}}} \right) \times {P_{\rm{b}}}} }}{{2 \times {R_{\rm{b}}}\left( {{\rm{SOC}}} \right)}}, $ | (12) |
式中:Eb(SOC)为随电池SOC变化的电动势,V;Rb(SOC)为随电池SOC变化的内阻,Ω。
电池荷电状态的计算公式为
| $ {\rm{SOC}} = \frac{{{Q_{\rm{c}}} - \int_0^t {{I_{\rm{b}}}{\rm{d}}t} }}{{{Q_{\rm{c}}}}}, $ | (13) |
式中Qc为电池的容量,A·h。
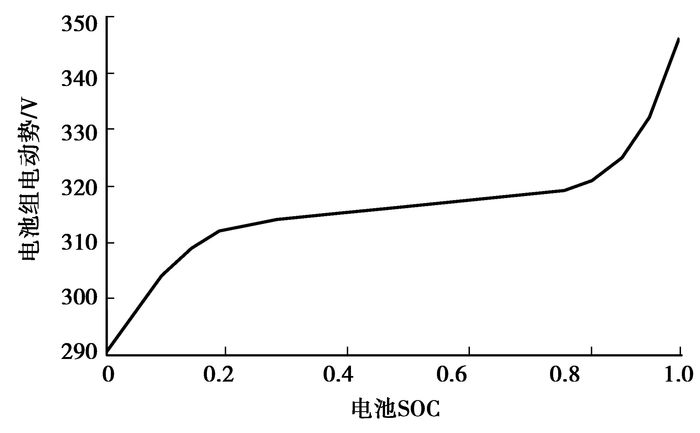
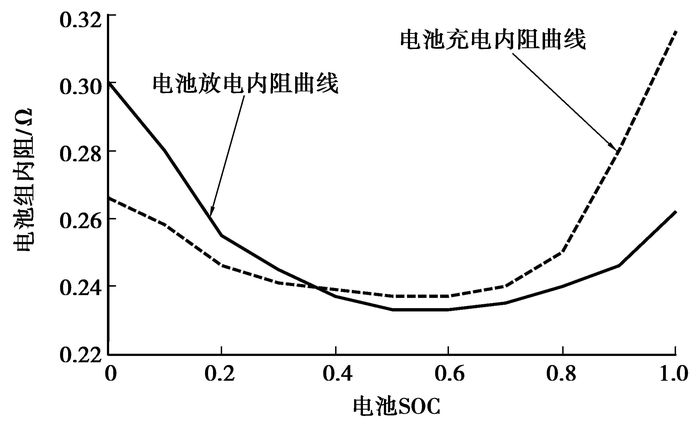
已知电池组SOC,可在电池组电动势模型和电池组内阻模型中插值得到Eb(SOC)、Rb(SOC)。电池组电动势模型和电池组内阻模型如图 5和6所示。
|
图 5 电池组电动势模型 |
|
图 6 电池组内阻模型 |
混合动力汽车的优化能量管理策略,本质就是在一定的约束条件下实现对整车燃油经济性的寻优控制过程,笔者采用动态规划算法进行混合动力系统全局优化控制问题的求解。动态规划算法是将已知循环工况分为N段,从而将混合动力汽车需求转矩分配的最优控制问题转化为一个多阶段决策问题。
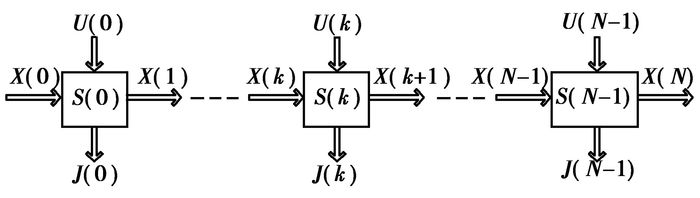
2.1 动态规划方程在本系统的动态规划求解过程中,将挡位ig、发动机转速ωe和电池荷电状态SOC设为状态变量,将电机扭矩Tm和油门开度θ定为控制变量。在k阶段的状态变量X(k)[ig(k),ωe(k),SOC(k)],控制变量U(k)[Tm(k),θ(k)],在满足约束条件下通过动态模型所确定的状态转移函数S(k)得到k+1阶段的状态变量X(k+1)[ig(k+1),ωe(k+1),SOC(k+1)],同时通过此过程得到k阶段的性能指标函数J(k)。如图 7所示动态规划状态量和控制量递推关系可描述为:
|
图 7 动态规划状态量和控制量递推关系图 |
k阶段的状态转移函数为
| $ X\left( {k + 1} \right) = S\left( k \right)\left[ {X\left( k \right),U\left( k \right)} \right]。$ | (14) |
通常,动态规划方法的阶段性能指标为每一阶段燃油消耗量Q的累计,即
| $ J\left( k \right)\left[ {X\left( k \right),U\left( k \right)} \right] = \sum\nolimits_{t = 0}^{N - 1} {Q\left[ {X\left( k \right),U\left( k \right)} \right]} 。$ | (15) |
这里所研究的混合动力汽车控制策略时,需考虑电池SOC维持平衡且需避免频繁换挡,故需在式(5)中分别加入两项附加代价函数LSOC和Lig,即
| $ {L_{{\rm{SOC}}}}\left( k \right)\left[ {X\left( k \right),U\left( k \right)} \right] = \beta {\left[ {{\rm{SOC}}\left( k \right) - {\rm{SO}}{{\rm{C}}_{{\rm{des}}}}} \right]^2}, $ | (16) |
式中SOCdes为目标SOC。
| $ {L_{{i_{\rm{g}}}}}\left( k \right)\left[ {X\left( k \right),U\left( k \right)} \right] = \gamma K\left\{ \begin{array}{l} K = 1,换挡;\\ K = 0,未换挡。\end{array} \right. $ | (17) |
增加两项附加代价函数后,式(15)变为
| $ \begin{array}{l} J\left( k \right)\left[ {X\left( k \right),U\left( k \right)} \right] = \alpha \sum\nolimits_{t = 0}^{N - 1} {Q\left[ {X\left( k \right),U\left( k \right)} \right]} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\beta {\left[ {{\rm{SOC}}\left( k \right) - {\rm{SO}}{{\rm{C}}_{{\rm{des}}}}} \right]^2} + \gamma K, \end{array} $ | (18) |
式中α、β、γ为权值系数。其中任何一个权值系数的增大,都增加了相关项在性能指标中的重要度。选取权值系数采用如下步骤:
1) α为参考基准,选取固定数值。
2) 估计性能指标中第1、2项的数量级,选取相同数量级的γ。
3) 选取适当的β以满足电池SOC在理想值范围。
4) 观察得到的换挡规律,如果不满意则调整γ然后重复步骤3。
通过上述分析,全局优化的控制策略问题转化为利用动态规划在一定约束条件下求解一系列最小值问题,如k(0<k<N-1)阶段时的性能指标函数递归方程可表示为其中f(N)=0。
| $ f\left( k \right) = \min \left[ {J\left( k \right)\left[ {X\left( k \right),U\left( k \right)} \right] + f\left( {k + 1} \right)} \right], $ | (19) |
其中,控制变量和状态变量应满足的约束条件为:
| $ \left\{ \begin{array}{l} {\omega _{{{\rm{e}}_{\min }}}} \le {\omega _{\rm{e}}} \le {\omega _{{{\rm{e}}_{\max }}}},\\ 0 \le {T_{\rm{e}}}\left( k \right) \le {T_{{e_{\max }}}}\left( {{\omega _{\rm{e}}}\left( k \right)} \right),\\ 0 \le {\omega _{\rm{m}}} \le {\omega _{{m_{\max }}}},\\ {T_{{{\rm{m}}_{\min }}}}\left( {{\omega _{\rm{m}}}\left( k \right)} \right) \le {T_{\rm{m}}}\left( k \right){ \le _{{{\rm{m}}_{\max }}}}\left( {{\omega _{\rm{m}}}\left( k \right)} \right),\\ {\rm{SO}}{{\rm{C}}_{\min }} \le {\rm{SOC}}\left( k \right) \le {\rm{SO}}{{\rm{C}}_{\max }},\\ {i_{\rm{g}}}\left( k \right) = \left\{ {0.78、0.96、1.31、2.05、3.67} \right\}。\end{array} \right. $ |
将求解过程控制在控制变量的约束范围及状态变量的约束范围内,分别把这两个范围定义为:容许控制集和可达状态集。
2.2 动态规划全局搜索算法动态规划算法求解过程主要包括逆向和正向计算两个部分。
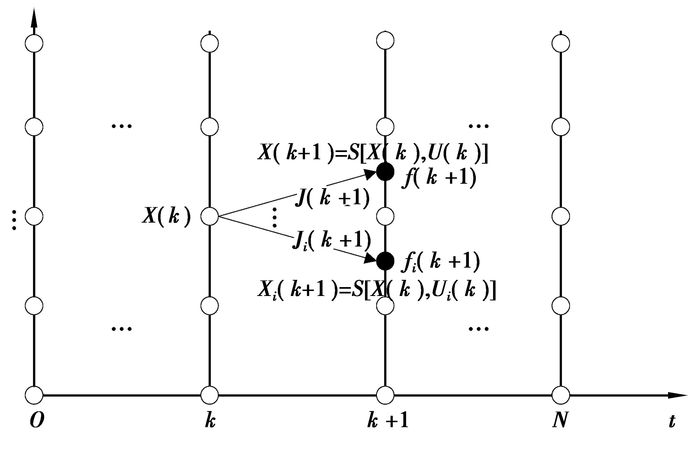
首先为逆向计算,即从N阶段开始到第1阶段结束。在容许控制集里对控制变量等分并离散化逐个取点,以k阶段的某一个网格点Xi(k),U(k)…Ui(k)…为例阐述逆向求解过程如图 8所示,根据状态变量的传递方程(14)可计算出X(k+1)…Xi(k+1)…,但由于X(k+1)…Xi(k+1)…不一定恰好在k+1时刻的状态值上,故需插值计算出相对应的性能指标函数f(k+1)…fi(k+1)…,其中k阶段的阶段性能指标函数为J(k)…Ji(k)…,然后根据式(19)取J(k)+J(k+1)…Ji(k)+fi(k+1)…的最小值,最小值即为k阶段上该网格点的性能指标函数f,最小值相对应的控制变量即为k阶段上该网格点最优控制变量U。重复上述过程计算得到k阶段上其他网格点的[U,f]。当k阶段所有网格点的计算完成,依次计算k-1阶段一直到第1阶段结束。
|
图 8 逆向计算 |
其次正向计算是从第1阶段开始至第N阶段结束,以逆向计算的结果为已知数据,由于第一阶段为初始阶段有且只有一个网格点,即直接读取第1阶段该网格点的[U,f],通过状态变量的传递方程(14)转到第2阶段某一网格点上,然后读取第2阶段该网格点的[U,f],通过状态变量的传递方程(14)转到第3阶段某一网格点上,重复上述过程依次计算一直到第N阶段结束。
正向计算完成后,动态规划算法结束。提取每个阶段的最优控制变量按顺序合并得到全局最优控制策略。
3 仿真结果分析全局最优控制策略得到后。应用MATLAB\Simulink在NEDC循环工况下,对所建立的基于动态规划的全局最优控制策略进行仿真验证。MTALAB\Simulink仿真验证模型中所涉及的仿真参数为:整备质量 m=1 350 kg,迎风面积A=2.28 m2,空气阻力系数CD=0.32,主减速器传动比io=3.93,车轮滚动半径Rw=0.295 m,滚动阻力系数f=0.013 5,电喷发动机JL475Q3,排量1.6 L,峰值功率72 kW。ISG电机,峰值功率30 kW。动力蓄电池为镍氢电池,额定电容量8.0 A·h,额定电压288 V。设置SOC初始值为0.5,运行仿真模型所得仿真结果如图 9~16所示。
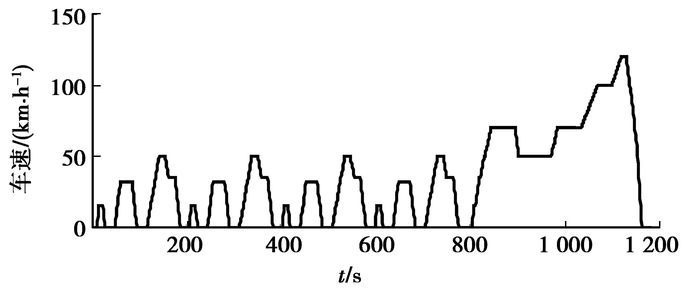
|
图 9 汽车车速 |
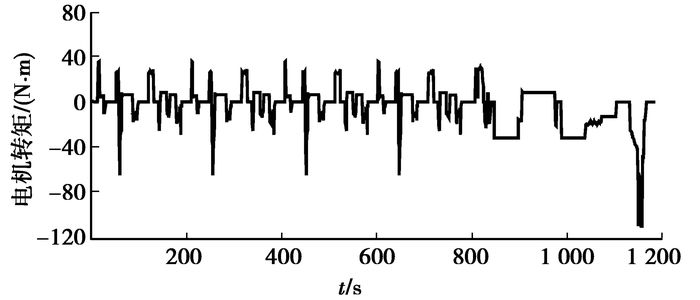
|
图 10 电机转矩 |
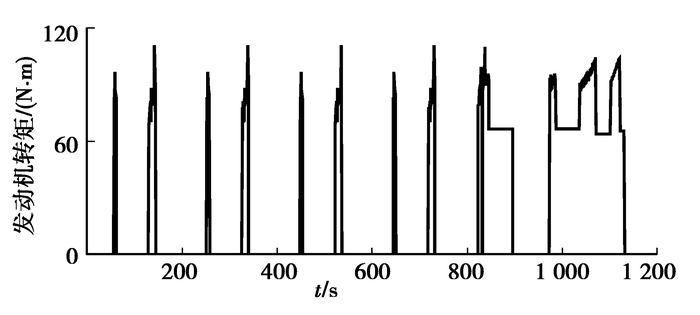
|
图 11 发动机转矩 |
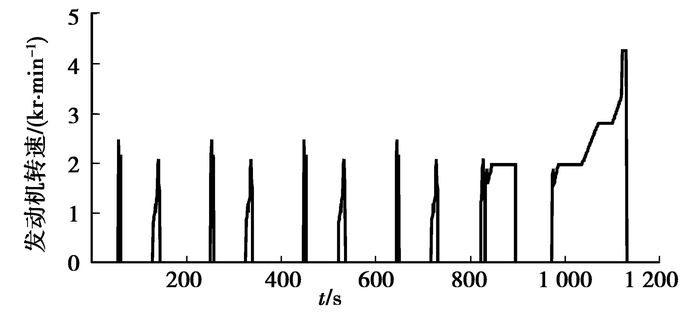
|
图 12 发动机转速 |
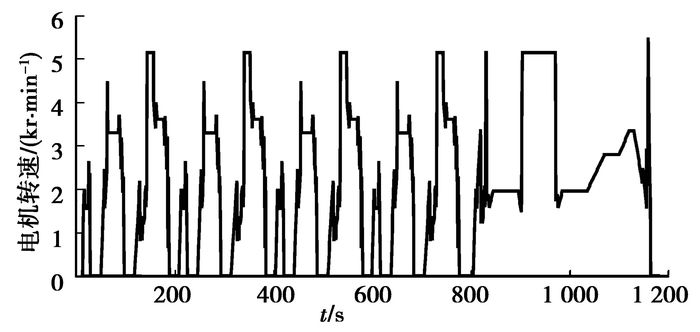
|
图 13 ISG电机转速 |
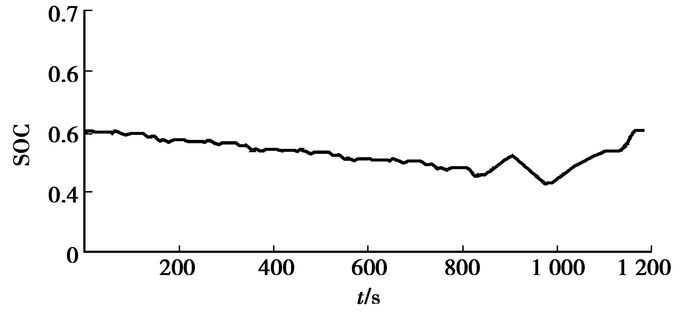
|
图 14 电池SOC |
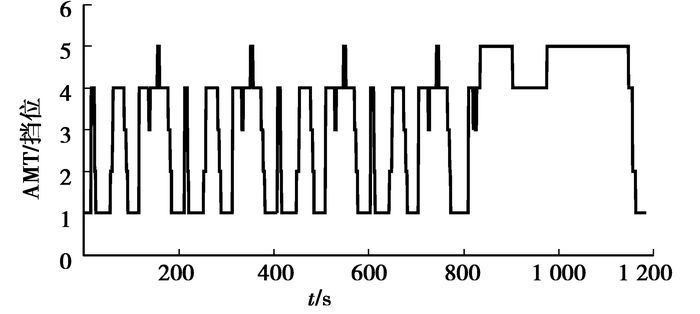
|
图 15 AMT变速器挡位 |
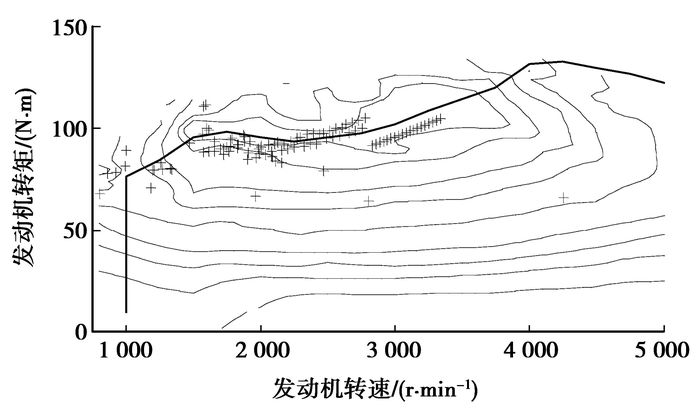
|
图 16 发动机工作点 |
从仿真计算结果看出,AMT挡位没有频繁的循环换挡现象,发动机工作点大致沿着最佳工作线在高效区域内运行,蓄电池SOC变化在合理范围内,且循环结束时SOC值相对初值基本平衡,NEDC循环仿真所得百公里油耗为5.52 L/100 km。与常规[16]ISG型混合动力汽车油耗5.95 L/100 km相比,燃油经济性提高了7.2%。与相对传统的基础车型[16]油耗8.564 L/100 km相比,燃油经济性提高了35.5%。基于DP的全局优化控制策略获得了显著的节油效果。
4 结语通过对一款ISG型速度耦合混合动力汽车进行动力学分析,建立了整个系统的数学模型,采用动态规划方法,设计了相匹配的全局优化控制策略,使该混合动力汽车在减少频繁换挡且保持电池SOC平衡的情况下,提高了燃油经济性,仿真结果表明:电池荷电状态能够在行驶循环工况中保持有效平衡,AMT挡位分布合理且没有频繁循环换挡,发动机的工作点在高效区域内分布,采用全局最优控制策略的新型ISG速度混合动力汽车NEDC百公里综合油耗为5.52 L/100 km,与传统的基础车型相比,燃油经济性提高了35.5%,从而验证了所建立的全局优化控制策略的有效性,为评价其他控制策略提供了参考,并为提炼出实时控制规则奠定了基础。
致谢 笔者对访学期间密西根大学彭辉教授在动态规划优化算法方面的协助表示感谢。
| [1] |
吴晓刚, 王旭东, 毛亮.
ISG型混合动力汽车能量管理模糊控制的研究[J]. 汽车工程, 2011, 33(7): 558–562, 568.
WU Xiaogang, WANG Xudong, MAO Liang. A research on the fuzzy control of energy management for an ISG hybrid vehicle[J]. Automotive Engineering, 2011, 33(7): 558–562, 568. (in Chinese) |
| [2] |
叶心, 秦大同, 胡明辉, 等.
ISG型中度混合动力轿车油门动态协调控制策略[J]. 重庆大学学报, 2010, 33(11): 1–7.
YE Xin, QIN Datong, HU Minghui, et al. Throttle dynamic coordinated control strategy of ISG type medium-HEV[J]. Journal of Chongqing University, 2010, 33(11): 1–7. DOI:10.11835/j.issn.1000-582X.2010.11.001 (in Chinese) |
| [3] |
张毅, 刘和平, 伍元彪.
并联混合动力汽车模糊多目标控制策略[J]. 重庆大学学报, 2013, 36(2): 75–84.
ZHANG Yi, LIU Heping, WU Yuanbiao. Multi-objective control strategy for parallel HEV using fuzzy logic[J]. Journal of Chongqing University, 2013, 36(2): 75–84. DOI:10.11835/j.issn.1000-582X.2013.02.013 (in Chinese) |
| [4] | Xiong W W, Zhang Y, Yin C L. Optimal energy management for a series parallel hybrid electric bus[J]. Energy Conversion and Management, 2009, 50(7): 1730–1738. DOI:10.1016/j.enconman.2009.03.015 |
| [5] | Poursamad A, Montazeri M. Design of genetic-fuzzy control strategy for parallel hybrid electric vehicles[J]. Control Engineering Practice, 2008, 16(7): 861–873. DOI:10.1016/j.conengprac.2007.10.003 |
| [6] | Park J, Park J H. Development of equivalent fuel consumption minimization strategy for hybrid electric vehicles[J]. International Journal of Automotive Technology, 2012, 13(5): 835–843. DOI:10.1007/s12239-012-0084-6 |
| [7] | Serrao L, Onori S, Rizzoni G. ECMS as a realization of pontryagin's minimum principle for HEV control[C]// Proceedings of the 2009 American Control Conference, June 10-12, 2009, St. Louis, MO. Piscataway:IEEE Press, 2009:3964-3969. |
| [8] | Gao J P, Zhu G M G, Strangas E G, et al. Equivalent fuel consumption optimal control of a series hybrid electric vehicle[J]. Proceedings of the Institution of Mechanical Engineers, 2009, 223(8): 1003–1018. |
| [9] | Paganelli G, Delprat S, Guerra T, et al. Equivalent consumption minimization strategy for parallel hybrid powertrains[C]//Proceedings of the IEEE 55th Vehicular Technology Conference, May 6-9, 2002, Birmingham, Alabama, USA. Piscataway:IEEE Press, 2002, 4:2076-2081. |
| [10] | Hui S. Multi-objective optimization for hydraulic hybrid vehicle based on adaptive simulated annealing genetic algorithm[J]. Engineering Applications of Artificial Intelligence, 2010, 23(1): 27–33. DOI:10.1016/j.engappai.2009.09.005 |
| [11] | Sundetr m O, Guzzella L, Soltic P, et al.Optimal hybridization in two parallel hybrid electric vehicles using dynamic programming[C]//Proceedings of the 17th IFAC World Congress:the International Federation of Automatic Control, July 6-11, 2008, Seoul, Korea.[S.l.]:IFAC, 2008:4642-4647. |
| [12] |
朱道伟, 谢辉, 严英, 等.
基于道路工况自学习的混合动力城市客车控制策略动态优化[J]. 机械工程学报, 2010, 46(6): 33–38.
ZHU Daowei, XIE Hui, YAN Ying, et al. Control strategy dynamic optimization of the hybrid electric bus based on driving cycle self-learning[J]. Journal of Mechanical Engineering, 2010, 46(6): 33–38. (in Chinese) |
| [13] | Romaus C, Gathmann K, Bocker J. Optimal energy management for a hybrid energy storage system for electric vehicles based on stochastic dynamic programming[C]//Proceedings of the Vehicle Power and Propulsion Conference, September 1-3, 2010, Lille, France. Piscataway:IEEE Press, 2010:1-6. |
| [14] | Johannesson L, Asbgard M, Egardt B. Assessing the potential of predictive control for hybrid vehicle powertrains using stochastic dynamic programming[C]// Proceedings of the 2005 IEEE Intelligent Transportation Systems, September 13-15, 2005, Tokyo, Japan. Piscataway:IEEE Press, 2005:366-371. |
| [15] | 余志生. 汽车理论[M]. 3版. 北京: 机械工业出版社, 2000. |
| [16] |
舒红, 蒋勇, 高银平.
中度混合动力汽车模型预测控制策略[J]. 重庆大学学报, 2010, 33(1): 36–41.
SHU Hong, JIANG Yong, GAO Yinping. Model predictive control strategy of a medium hybrid electric vehicle[J]. Journal of Chongqing University, 2010, 33(1): 36–41. DOI:10.11835/j.issn.1674-4764.2010.01.008 (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


