2. 国网济源供电公司, 河南 459000
2. State Grid Jiyuan Electric Power Company, Henan 459000, China
配电系统中,单相接地故障是电网运行故障的主要形式,甚至大部分的相间故障也是由单相故障发展而来的。单相接地故障的类型分为金属性接地和高阻接地。其中高阻接地故障发生时,三相线电压几乎还是对称,同时故障电流很小,故障特征不明显,很难对特征量进行准确的提取,从而加大了高阻故障检测的难度。高阻接地故障会影响输配电系统正常运行,对弧光接地故障来说由于空气游离的缘故,接地阻抗变化很大,使现有保护反复启动、恢复,可能会导致相邻线路、设备的保护越级跳闸,使电力系统出现更严重的故障。在故障停电对用户恢复供电时,高阻故障会造成火灾、人身触电等严重后果,给生命财产带来损失,因此,高阻抗故障的检测十分重要。
目前对高阻接地故障的研究主要集中于线路高阻接地保护,文献[1]经过现场实验,建立了发生在沙地上伴随有电弧的高阻抗故障的模型,并指出采用线电流的三次谐波来检测伴随有电弧的高阻抗故障。文献[4]利用卡尔曼滤波方法对高阻接地故障进行了研究;文献[7]选取相电流2次、3次、5次谐波相对于相电流有效值的比值以及3次谐波的相位作为高阻抗故障的判据,采用模糊逻辑进行判别。此外,人工神经网络也被尝试用于高阻故障检测,但由于神经网络需要大量训练样本,目前难以应用于电力系统实际中。
笔者提出了一种基于离散小波变换的高阻故障识别方法,通过对高阻故障发生时生成的残余电压电流的特征量进行提取,利用残余电压电流的离散小波细节系数进行故障检测。
1 故障识别判据 1.1 线路的等效模型分析电力系统中电力线路的数学模型是以电阻、电抗、电纳、电导表示的等值电路。电力线路的参数是均匀分布的,配电线路一般不长,需要分析的只是端点的电压、电流、功率等,通常不考虑线路的分布参数影响。在没有特殊要求的情况下,一般采用∏型等值电路,见图 1。
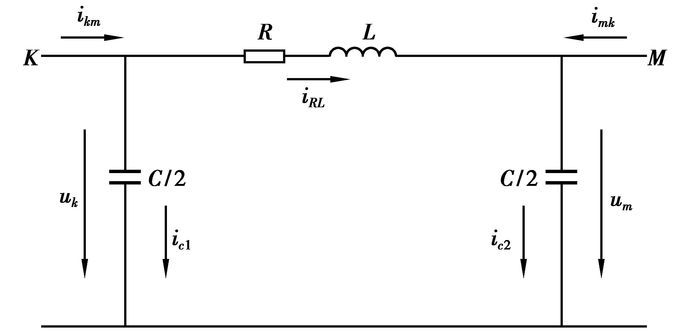
|
图 1 线路的∏型等值电路 |
对于线路∏型等值电路的电压、电流关系描述如下:
| $ {i_{c1}} = \left( {c/2} \right) \times \frac{{{d_{uk}}}}{{{d_t}}}, $ | (1) |
| $ {i_1} = \left( {c/2} \right) \times \frac{{{d_{um}}}}{{{d_t}}}, $ | (2) |
| $ L\frac{{{\rm{d}}{i_{RL}}}}{{{{\rm{d}}_t}}} + R{i_{RL}} = {u_k} - {u_m}, $ | (3) |
| $ {i_{km}} = {i_{c1}} + {i_{RL}}, $ | (4) |
| $ {i_{mk}} = {i_{c2}} - {i_{RL}}, $ | (5) |
将式(1)、(2)、(3) 差分后,根据式(4)、(5) 得到:
| $ \begin{array}{l} {i_{km}}\left( t \right) = \left( {C/\Delta t + {G_{RL}}} \right){u_k}\left( t \right) - {G_{RL}}{u_m}\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;{I_{RL}}\left( {t - \Delta t} \right) + {I_{cl}}\left( {t - \Delta t} \right), \end{array} $ | (6) |
| $ \begin{array}{l} {i_{nk}}\left( t \right) = \left( {C/\Delta t + {G_{RL}}} \right){u_m}\left( t \right) - {G_{RL}}{u_k}\left( t \right) - \\ \;\;\;\;\;\;\;\;\;\;\;{I_{RL}}\left( {t - \Delta t} \right) + {I_{c2}}\left( {t - \Delta t} \right)。\end{array} $ | (7) |
其中:
| $ {G_{RL}} = 1/\left( {2L/\Delta t + R} \right), $ | (8) |
| $ {G_c} = C/\Delta t, $ | (9) |
| $ \begin{array}{l} {I_{RL}}\left( {t - \Delta t} \right) = \left( {1 - {G_{RL}}R} \right){i_{RL}}\left( {t - \Delta t} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{G_{RL}}\left( {{u_k} - {u_m}} \right), \end{array} $ | (10) |
| $ {I_{c1}}\left( {t - \Delta t} \right) = {G_c}{u_k}\left( {t - \Delta t} \right) - {i_{c1}}\left( {t - \Delta t} \right), $ | (11) |
| $ {I_{c2}}\left( {t - \Delta t} \right) = {G_c}{u_m}\left( {t - \Delta t} \right){i_{c2}}\left( {t - \Delta t} \right)。$ | (12) |
线路的暂态等值计算网络如图 2所示。
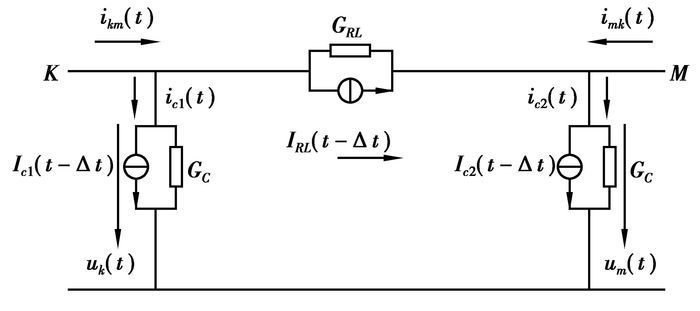
|
图 2 线路∏型暂态等值电路 |
傅里叶算法、频域分析法或单纯的时域分析法都不足以精确地描述暂态电压电流的非平稳信号。小波分析是解决这一问题的良好工具,它通过把信号分解为不同位置和尺度的小波函数,使其在时域和频域都具有良好的局部化性能。小波分析可以对暂态信号进行多尺度分解,然后进行不同量谱上的分析,提取不同量谱上的特征作为识别依据。为尽量减少滤波器产生的混叠,必须采用分频严格的小波。同时,根据继电保护的实时性要求,母小波的选取应考虑具有紧支性。
通常如果Ψ(t)∈L2(R),其傅里叶变换为
| $ {C_\mathit{\Psi }} = \int\limits_{ - \infty }^{ + \infty } {{{\left| w \right|}^{ - 1}}{{\mathit{\hat \Psi }}_{\left( w \right)}}\left| {^2} \right.{\rm{d}}w} < \infty , $ | (13) |
即CΨ有界,则称Ψ为一个基小波或母小波。将母小波经过伸缩和平移后,就可以得到一个小波序列。
| $ {\mathit{\Psi }_{a,b}}\left( t \right) = {\left| a \right|^{ - 1/2}}\mathit{\Psi }\left( {\frac{{x - b}}{a}} \right), $ | (14) |
式中:a,b∈ R且a≠0。称a为伸缩因子,b为平移因子。在处理数字信号问题时,经常采用的是小波分析的离散形式,即离散小波变换(DWT)。DWT可以通过离散化CWT中的伸缩因子a和平移因子b得到。通常取a=a0m,b=nb0a0m,m、n∈Z代入上式可得
| $ {\mathit{\Psi }_{m,n}}\left( t \right) = {\left| a \right|^{ - m/2}}\mathit{\Psi }\left( {a_0^{ - m}t - n{b_0}} \right),m,n \in Z; $ | (15) |
这时的小波函数就是离散小波。相应的离散小波变换为
| $ \left( {{W_\psi }f} \right)\left( {a,b} \right) = {\left| a \right|^{ - m/2}}\int\limits_{ - \infty }^{ + \infty } {f\left( t \right)\overline {\mathit{\Psi }\left( {{a^{ - m}} - n{b_0}} \right)} {\rm{d}}t} 。$ | (16) |
当取a0=2,b0=1时可得二进小波:
| $ {\mathit{\Psi }_{m,n}}\left( t \right) = {2^{ - m/2}}\mathit{\Psi }\left( {{2^{ - m}}t - n} \right),m,n \in Z; $ | (17) |
式(13) 是小波函数应满足的基本条件,显然,小波函数有无穷多个,故小波基也有无穷多组。因为不同的小波基具有不同的时频特征,用不同的小波基分析同一个问题会产生不同的结果,故小波分析在应用中便存在一个小波基或小波函数的选取和优化问题。笔者根据小波函数的特征,选择最能反映故障征兆的小波基。
在小波基函数的选择上,使用MATLAB小波工具箱对一系列的小波进行了实验,测试发现使用db3小波提取高阻故障特征信号比较明显,笔者对数据的处理都是在db3小波的基础上进行的。仿真模型的采样频率为f=20 kHz。对采集到的信号进行处理时,使用db3小波对信号进行5层分解,分别得到d1、d2、d3、d4、d5等细节系数,经过仿真计算分析,以图 3数据为例,计算各层分解系数的标准方差得到D(d1)=0.009 913 495,D(d2)=0.011 966 826,D(d3)=0.012 204 585;标准方差的计算结果表明d3系数的离散程度最高,也最能够表征故障时的特征量。
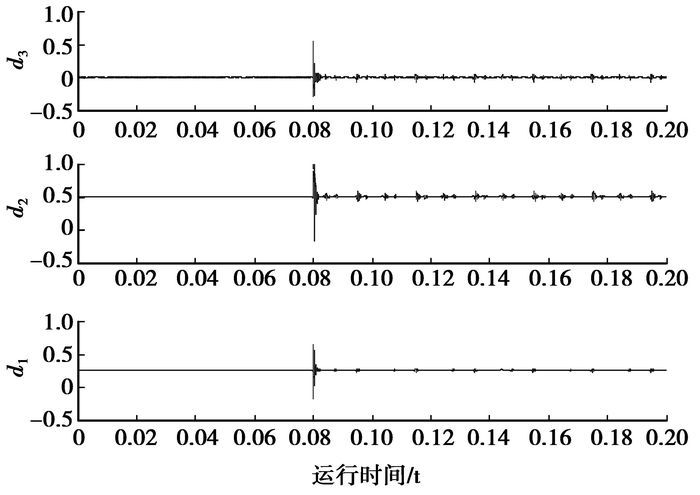
|
图 3 仿真系统故障段时d1、d2、d3细节系数 |
暂态信号中包含了大量反映故障性质的信息,电压、电流中不同频率分量所含能量的差异,为故障特征分析提供了依据。中性点不接地配网的接地故障识别可以使用故障发生时所产生的暂态信号,可以定义为残余电压和残余电流。
| $ {u_{\rm{r}}} = {u_1} + {u_2} + {u_3},{i_{\rm{r}}} = {i_1} + {i_2} + {i_3}, $ | (18) |
其中:ur为残余电压;ir为残余电流;u1、u2、u3为相电压;i1、i2、i3为相电流。
故障识别的流程图如图 4所示,为找到表征故障特征的特征量定义:
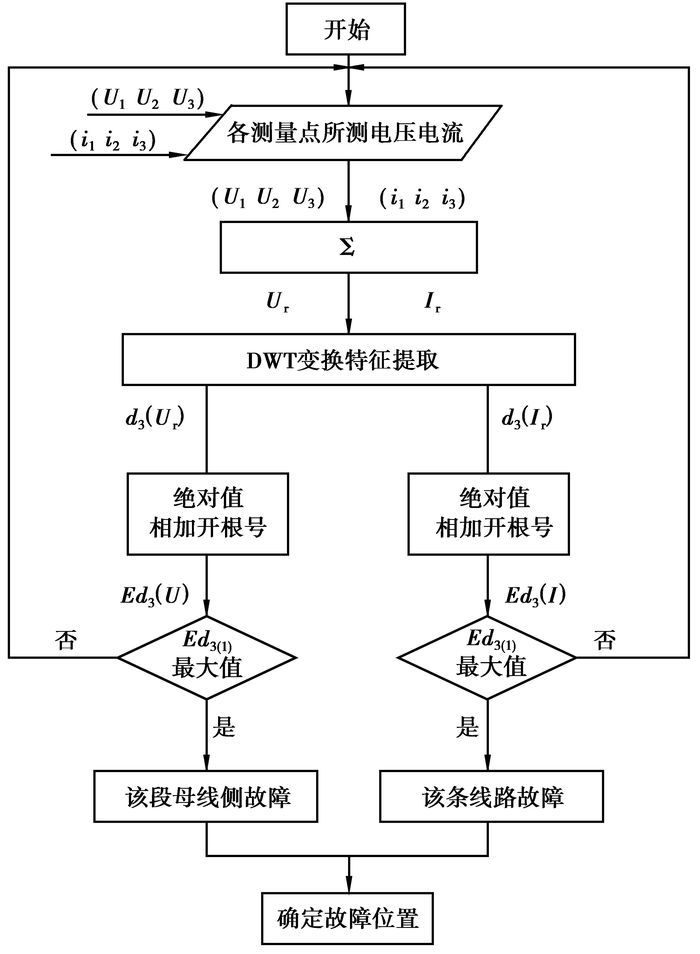
|
图 4 高阻故障识别流程图 |
| $ {E_{di\left( k \right)}} = \sqrt {\sum\limits_{h = k - N + 1}^k {\left| {{d_{i\left( k \right)}}} \right|} } 。$ | (19) |
运用式(19) 对小波处理后的小波细节系数进行加权计算,得到关于细节系数的量谱Ed1(u)、Ed2(u)、Ed3(u)分别表征d1、d2、d3等的特征量,该特征量相对于幅值微小的暂态信号具有较强的表征能力。其中di(k)是残余电压和残余电流的di小波系数。N是20 ms浮动时间窗所覆盖的采样点数,由于采样频率为20 kHz,采样周期为0.000 05 s,因此浮动窗所覆盖的采样点N=400。
故障识别算法的具体步骤如下:
① 采集每个测量点的相电压u1、u2、u3,相电流i1、i2、i3。
② 经过求矢量和ur=u1 +u2 +u3,ir=i1 +i2 +i3,计算出残余电压ur和残余电流ir的值。
③ 用db3母小波对相关的ur和ir进行离散小波分解重构,提取d3小波细节系数。
④ 对d3小波细节系数绝对值进行20 ms固定浮动时间窗的计算,按量谱计算
⑤ 通过以上信息综合判断确定最终的高阻故障线路位置。
2 仿真系统笔者对配电网相关的高阻抗弧光故障进行仿真,仿真系统可以分为两个主要部分:配电网线路模型和故障模型。
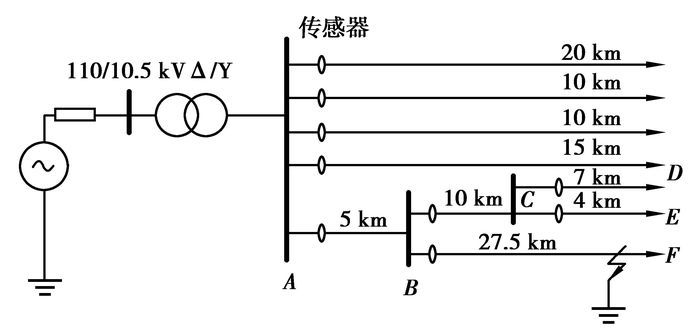
2.1 配网系统示意图图 5是5馈线中性点非有效接地的10 kV配网系统,该系统由单电源供电,馈线接线模式使用的是单辐射接线,这种接线模式是中国配电系统中尤其是农村电网广泛使用的接线方式,由于该系统结构简单,供电可靠性不高,容易发生典型性故障。笔者利用PSCAD仿真平台对该系统进行了仿真[9-10]。
|
图 5 配电网模拟系统示意图 |
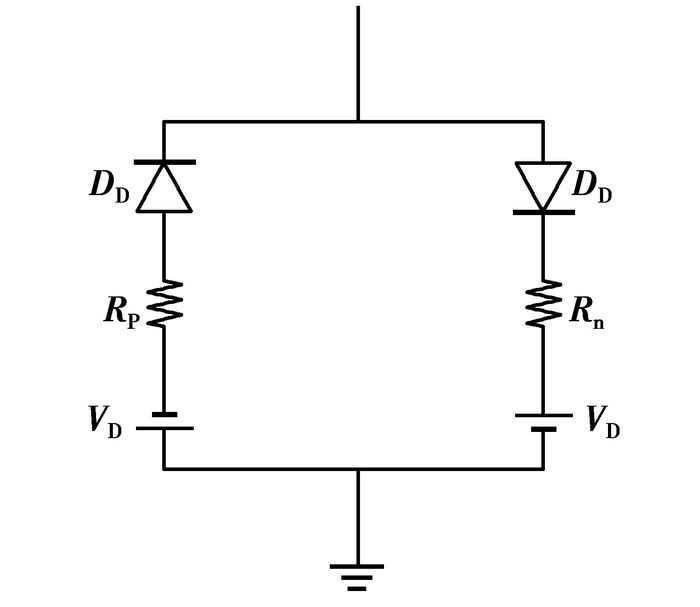
仿真系统中故障模型的建立对仿真结果有比较大的影响,笔者所用的故障模型如图 6所示[7-8],模型包括两个直流电源vn和vp,直流源表示配电线路弧光放电时的电压,二极管和电源之间的两个电阻Rp和Rn表示故障发生时的接地电阻,为了模拟不对称电流Rp和Rn的阻值选择不同的值。当线电压大于正直流电压vn时,故障电流就流向大地。当线电压低于负直流电压vp时,故障电流反向流动。当线电压的值介于vn和vp之间时,线电压被vp或vn抵消,此时没有故障电流流过。
|
图 6 高阻故障模型 |
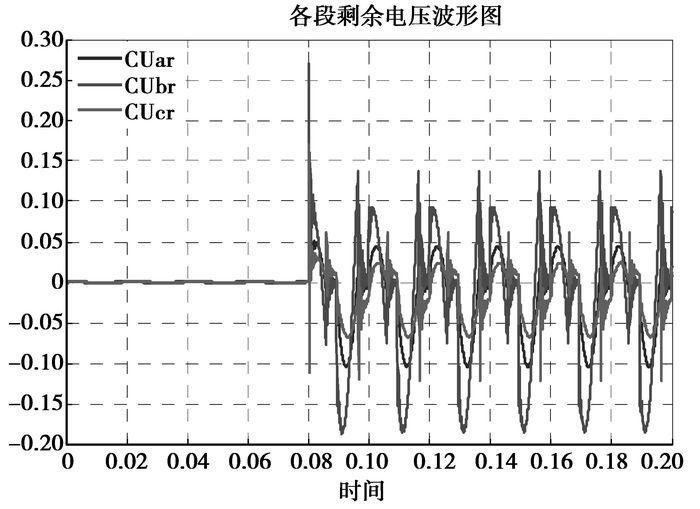
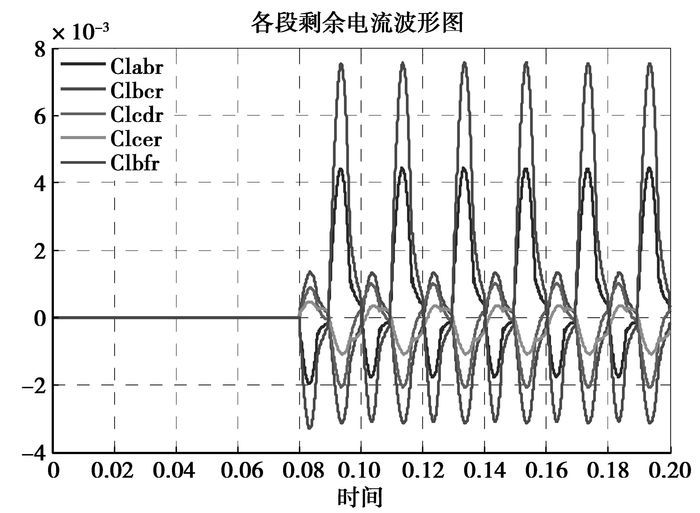
图 5所示的配电网模拟系统中,故障发生在分支线路BF段的末端,故障发生的时刻是0.08 s时,相对应的故障残余电压和残余电流的波形如图 7和图 8所示。从图 7中可以看出当故障发生前,母线A、B、C三段的残余电压趋近于0,说明各段母线的各相电压趋近于三相对称运行,也就是没有故障的状态。当0.08 s的时刻故障发生后,A、B、C三段母线的残余电压发生了跃变,三相电压成不对称运行状态。从图中可以看出该故障状态下,母线B侧的残余电压值跃变最大,母线A、C侧的残余电压幅值相对小很多。图 8是故障发生在BF段时,各个分支线路的残余电流波形。故障本身所在的BF分支,残余电流值最大,其次是与其相连接的上一级分支线路AB段的残余电流也比较大,这符合故障状态下线路分支电流的分布规律。
|
图 7 故障发生在BF段时的残余电压波形 |
|
图 8 故障发生在BF段时的残余电流波形 |
笔者对数据的处理都是在db3小波的基础上进行的。仿真模型的采样频率为f=20 kHz。当BF段故障时,采集到的各段母线电压和支路电流经过多分辨分解重构得到残余电压和残余电流的d3细节系数,图 9图 10分别是各段母线残余电压和各个支路残余电流的d3细节系数。
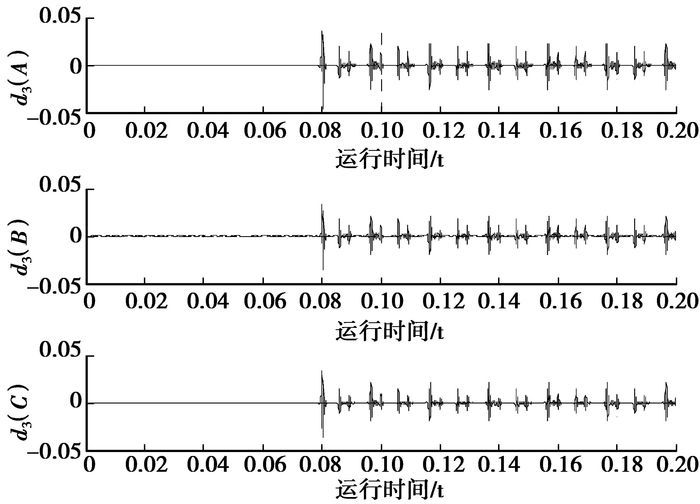
|
图 9 各段母线残余电压的d3细节系数 |

|
图 10 各个支路残余电流的d3细节系数 |
经过小波多分辨率分析得到了残余电压和残余电流的d3小波细节系数,用下述离散形式对小波系数进行处理:
| $ {E_{di\left( k \right)}} = \sqrt {\sum\limits_{h = k - N + 1}^k {\left| {{d_{i\left( k \right)}}} \right|} } 。$ | (19) |
图 11是母线A、B、C段Ed(i)量谱特征波形。从图上可以清楚地识别最大值是Eb,也就是故障发生时母线B段的残余电压值最大,由此可以得出故障发生在母线B段侧。图 12是分支线路ab、bc、cd、ce、bf的Ed(i)量谱特征波形,从图上可以得出最大值Ebf,故障发生时分支线路bf段的残余电流值最大,由此得出故障发生在BF段。综合残余电压和残余电流的小波系数特征波形,判断故障发生在母线B侧和线路分支BF上,最终识别出故障位置具体位置在分支BF上,与仿真设定的故障位置相同。
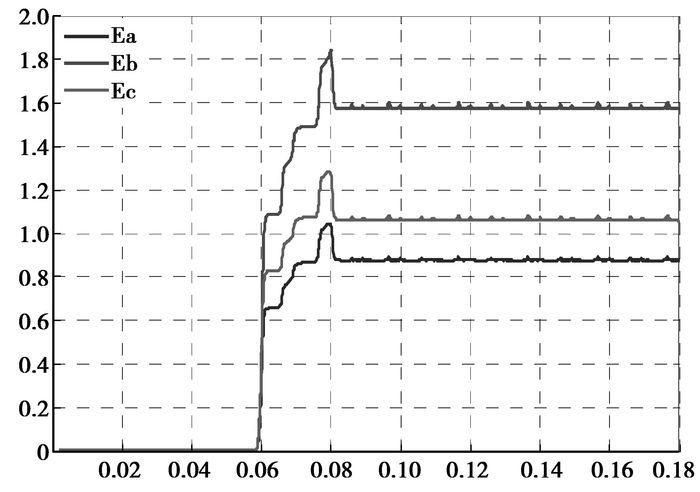
|
图 11 各分支线路残余电流的Ed(i)波形 |
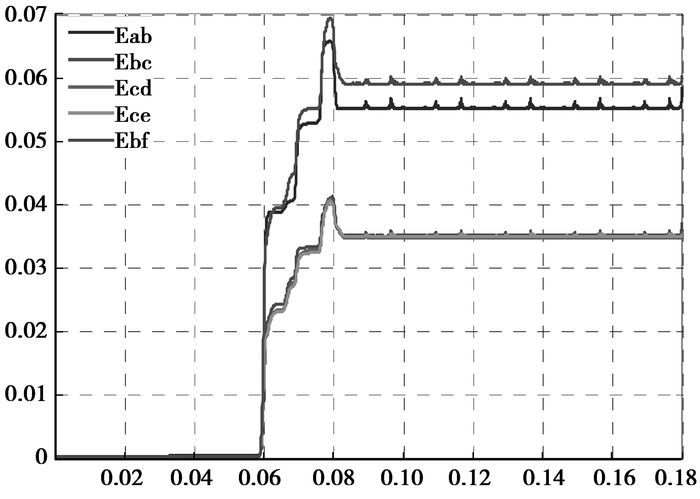
|
图 12 各段母线残余电压的Ed(i)波形 |
笔者在PSCAD仿真平台中模拟配电网系统,建立高阻故障模型。对采集到的故障信号进行离散分析,抽取故障信号的特征量,利用小波变换多分辨率分析,对分层的小波细节系数的绝对值进行浮动时间窗覆盖的叠加,构成故障识别的判据。理论分析与PSCAD仿真结果表明,该算法不仅运算速度快,而且几乎不受故障位置、故障初始角的影响,能够快速灵敏、有选择性地检测高阻接地故障。从继电保护的角度分析,识别故障性暂态信号具有重要意义,该判据可以作为各种暂态保护的附加判据,以提高保护的可靠性和速度。
| [1] | Lien K Y, Chen S L, Liao C J, et al. Energy variance criterion and threshold tuning scheme for high impedance fault detection[J]. IEEE Transactions on Power Delivery, 1999, 14(3): 810–817. DOI:10.1109/61.772319 |
| [2] | Chan T W D, Xia Y B. A novel technique for high impedance fault identification[J]. IEEE Transactions on Power Delivery, 1998, 13(3): 738–744. DOI:10.1109/61.686968 |
| [3] | Kim C H, Kim H Y, Ko Y H, et al. .A novel fault-detection technique of high-impedance arcing faults in transmission lines using the wavelet transform[J]. IEEE Transactions on Power Delivery, 2002, 17(4): 921–928. DOI:10.1109/TPWRD.2002.803780 |
| [4] | Girgis A A, Chang W, Makram E B. Analysis of high-impedance fault generated signals using a Kalman filtering approach[J]. IEEE Transactions on Power Delivery, 1990, 5(4): 1714–1724. DOI:10.1109/61.103666 |
| [5] |
陈小勤, 何正友, 符玲.
基于小波能谱的电力暂态信号分类识别方法[J]. 电网技术, 2006, 30(17): 59–63.
CHEN Xiaoqin, HE Zhengyou, FU Ling. Electric power transient signals classification and recognition method based on wavelet energy spectrum[J]. Power System Technology, 2006, 30(17): 59–63. DOI:10.3321/j.issn:1000-3673.2006.17.011 (in Chinese) |
| [6] |
曾祥军, 张小丽, 马洪江.
基于小波包能量谱的电网故障行波定位方法[J]. 高电压技术, 2008, 34(11): 2311–2316.
ZENG Xiangjun, ZHANG Xiaoli, MA Hongjiang. Traveling wave fault location method for power grids based on wavelet packet energy spectra[J]. High Voltage Engineering, 2008, 34(11): 2311–2316. (in Chinese) |
| [7] | Yong S, Rovnyak S M. Decision tree-based methodology for high impedance fault detection[J]. IEEE Transactions on Power Delivery, 2004, 19(2): 533–536. DOI:10.1109/TPWRD.2003.820418 |
| [8] | Civanlar S, Grainger J J, Yin H, et al. Distribution feeder reconfiguration for loss reduction[J]. IEEE Transactions on Power Delivery, 1988, 3(3): 1217–1223. DOI:10.1109/61.193906 |
| [9] | Elkalashy N I, Lehtonen M, .Darwish H A, et al. DWT-based detection and transient power direction-based location of high-impedance faults due to leaning trees in unearthed MV networks[J]. IEEE Transactions on Power Delivery, 2008, 23(1): 94–101. DOI:10.1109/TPWRD.2007.911168 |
| [10] | Elkalashy N I, Lehtonen M, Darwish H A, et al. DWT-based extraction of residual currents throughout unearthed MV networks for detecting high-impedance faults due to leaning trees[J]. European Transactions on Electrical Power, 2007, 17(6): 597–604. DOI:10.1002/(ISSN)1546-3109 |
| [11] | Elkalashy N I, Lehtonen M, Darwish H A, et al. Modeling and experimental verification of a high impedance arcing fault in MV networks[C]//Proceedings of IEEE/PES, Power Systems Conference and Exposition, October 29-November 1, 2006, Atlanta, Georgia, USA. Piscataway:IEEE Press, 2006:1950-1956. |
| [12] | Elkalashy N, Lehtonen M, Darwish H, et al. Electromagnetic Transients due to a High Impedance ArcingFault in MV Networks[C]. International Conference on Electromagnetic Disturbances, EMD 2006, 27-29 Sep., Kaunas. |
| [13] | Nordman M M, Korhonen T. Design of a concept and a wireless ASIC sensor for locating earth faults in Unearthed electrical distribution networks[J]. IEEE Transactions on Power Delivery, 2006, 21(3): 1074–1082. DOI:10.1109/TPWRD.2006.874637 |
| [14] | Sedighi A R, Haghifam M R, Malik O P, et al. High impedance fault detection based on wavelet transform and statistical pattern recognition[J]. IEEE Transactions on Power Delivery, 2005, 20(4): 2414–2421. DOI:10.1109/TPWRD.2005.852367 |
| [15] | Wai D C T, Xia Y B. A novel technique for high impedance fault identification[J]. IEEE Transactions on Power Delivery, 1998, 13(3): 738–744. DOI:10.1109/61.686968 |
| [16] |
周念成, 刘家伟, 赵渊, 等.
消弧线圈接地系统暂态能量选线新方法[J]. 重庆大学学报, 2009, 32(12): 1425–1430.
ZHOU Niancheng, LIU Jiawei, ZHAO Yuan, et al. Novel method for fault line selection in arc suppression coils system using transient energy[J]. Journal of Chongqing University, 2009, 32(12): 1425–1430. DOI:10.11835/j.issn.1000-582X.2009.12.011 (in Chinese) |
| [17] |
李新, 李景丽, 张从力, 等.
多频带分析的配电网单相接地故障选线[J]. 重庆大学学报, 2008, 31(10): 1143–1148.
LI Xin, LI Jingli, ZHANG Congli, et al. Detecting a fault line under a single-phase to ground of distribution network based on analysis of multi-frequency bands[J]. Journal of Chongqing University, 2008, 31(10): 1143–1148. DOI:10.11835/j.issn.1000-582X.2008.10.012 (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

