目前, 风能作为一种可再生清洁能源, 是解决环境与能源双重压力的重要手段之一, 近年来, 风力发电在中国发展迅猛, 截止2009年底, 并网发电的风机机组装机容量达到1 613万kW。但是, 其长时间、高频率、大尺度的随机出力波动将给电网的安全运行带来很大的风险[1], 同时, 也对并网变流器的可靠性构成严峻挑战, 文献[2]指出, 出力波动将导致并网变流器中电力电子器件, 经历持久的剧烈结温变化冲击, 严重影响到电力电子器件的可靠性和寿命, 逐渐引起国内外学者的关注[3]。相对其他电力电子器件, 绝缘栅双极晶体管(insulated gate bipolar transistor, IGBT)集成了电力BJT和电力MOSFET各自的优点, 是最具有发展前景的关键电力电子器件之一。目前, 通流能力和耐压水平已经达到6.5 kV/ 3.6 kA的水平[4], 广泛应用到风力发电领域实现电能输出[5]。因此, 研究IGBT的可靠性问题, 对促进风电的发展具有积极的作用, 成为近年研究的热点, 有大量关于IGBT可靠性问题的成果报道, 大致分为两类:首先是失效机理的研究, 明确主要的失效原因和模式[6-8];其次是运行过程中IGBT故障诊断[9-15]以及可靠性衰退程度的评估[3, 16, 17], 在很大程度上促进了IGBT可靠性问题的研究, 使其至今方兴未艾。不过, 上述研究尚不充分, 尤其是运行中IGBT模块可靠性衰退程度的评估, 尽管已经提出一些评估方法和相应的寿命预测模型, 但是尚存在一定的局限, 至今还没有应用报道, 这主要是由于商业化的IGBT多以模块的形式密闭封装, 造成与可靠性衰退相关信息的缺失。
文献[6, 18]研究提示:IGBT模块的老化, 是不断地经受电、热冲击累积作用的缓慢过程, 在故障前, 内部已经出现某些损伤, 导致部分铝键合线断裂等缺陷的发生, 在一定程度上降低了IGBT模块的性能, 相应地增加了IGBT模块故障的风险, 但IGBT模块仍然可以运行, 不具备故障特征, 现有的故障诊断方法无法检测。因此, 有必要研究辨识IGBT模块缺陷的方法, 既可视作故障诊断的进一步提高, 也可看作粗略的可靠性衰退评估。
此外, 缺陷对IGBT模块的影响, 还涉及辅助电路门极驱动, 即IGBT模块中器件内部门极寄生元件参数的变化, 其外部表现是门极端子处电压信号的变化, 相对于主电路的高电压、大电流而言, 缺陷对门极电压的影响比较明显, 也容易测量, 可被用来定性逆向判断IGBT模块是否存在缺陷, 故笔者引入时间序列的DTW(dynamic time warping)算法, 计算缺陷前后门极电压序列相似度的变化, 来辨识IGBT模块的缺陷。DTW具有很好的鲁棒性, 对测量噪声不敏感, 能够提高辨识的精度。实验结果表明, 该方法能够及时识别IGBT模块的缺陷, 为维护赢得宝贵时间, 具有很好的应用价值。
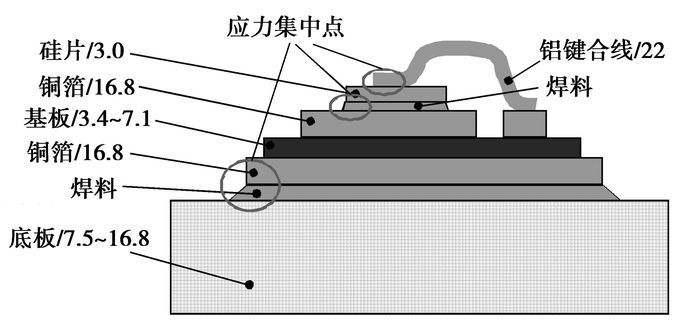
1 缺陷对IGBT模块门极电路的影响 1.1 IGBT模块缺陷分析文献[6, 19]给出了IGBT模块缺陷形成的两个主要因素:热冲击和强电场应力。其中, 热冲击是由IGBT模块组成材料的热膨胀系数不一致造成的, 典型IGBT模块的剖面图如图 1所示, 主要包括:硅片、基板、底板、铝键合线等[20], 由于IGBT模块功耗的存在以及负荷变化, 运行中结温波动是无法避免的, 当结温波动超出一定范围, 将在图 1所示的材料热膨胀系数相差比较大的铝键合线与硅片结合处和焊料层, 产生超出塑性形变的应力集中, 导致铝键合线断裂和焊料层开裂;而强电场应力的产生, 与门极静电放电(ESD)和集电极过电压有关, 会激发热载流子。
|
图 1 IGBT模块的剖面图 注:图中数字表示材料对应的热膨胀系数(1×10-6/℃) |
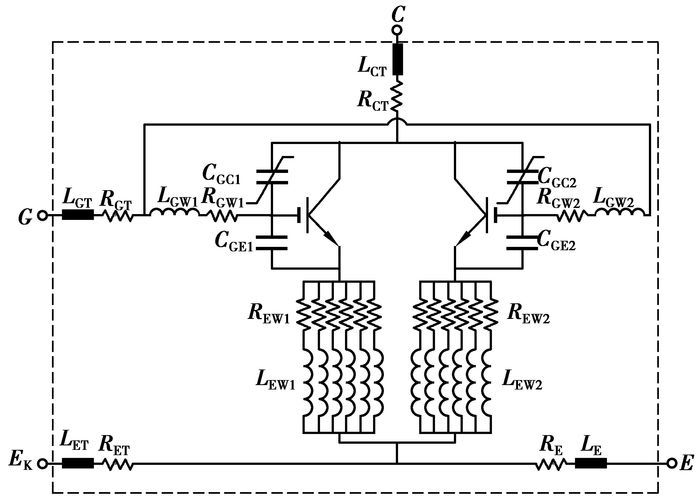
缺陷主要影响IGBT模块中器件内部门极寄生元件的参数, 如图 2所示, 图中LGT、RGX分别表示门极端子引线的寄生电感和电阻;LGW、RGW分别表示门极铝键合线的寄生电感和电阻;LEW、REW分别表示发射极铝键合线的寄生电感和电阻;LET、RET分别表示发射极辅助端子引线的寄生电感和电阻;LE、RE分别表示发射极端子引线的寄生电感和电阻;LCT、RCT分别表示集电极端子引线的寄生电感和电阻;CGE表示门射极寄生电容;CGC表示门集极寄生电容, CCE表示集射极寄生电容, 其中的寄生参数LCT、RCT及CCE与门极电路无关[21]。
|
图 2 IGBT器件等效电路示意图 注:数字表示组成IGBT器件的不同硅片 |
在IGBT模块的缺陷中, 焊料层开裂会减少有效导热面积, 导致IGBT模块结温升高[17], 而激发热载流子, 同强电场应力损伤机理相同, 会影响门射极之间的SiO2绝缘层, 改变门极结电容[22-23];铝键合线脱落除了很明显地改变门极寄生电感和寄生电阻参数外[24-25], 还可能影响IGBT模块的整体布局, 从而涉及门极电容。因为单位面积硅片通流能力的限制, 器件内多硅片并联模式被广泛采用[6], 如图 2所示, 本例中的IGBT器件都由两对IGBT-FWD硅片并联构成。若在热冲击累积作用下, 其中一个硅片的联结铝键合线全部断裂, 则该IGBT硅片失效, 将会改变IGBT模块门极结电容的构成及大小。
2 DTW算法及应用 2.1 DTW算法原理DTW是一种柔性算法, 能够对数据长度不同的时间序列进行匹配, 解决动态模式的相似度量和分类[26-28]。其实质是运用动态规划思想, 利用局部最优化处理, 寻找一条路线, 沿着这条路径, 两时间序列之间的距离最短。定义这个最短距离为两序列的相似度, 其值越小匹配程度越好。文献[29]给出了DTW算法的原理, 对于参考时间序列R和检测时间序列T:
| $\begin{align} & R=[{{r}_{1}},\text{ }{{r}_{2}},\text{ }\ldots {{r}_{i}},\text{ }\ldots {{r}_{n}}], \\ & T=[{{t}_{1}},\text{ }{{t}_{2}},\text{ }\ldots {{t}_{j}},\text{ }\ldots {{t}_{m}}]; \\ \end{align}$ | (1) |
其中:n和m分别为序列R和T的维数, 定义两序列元素之间的距离δ(i, j)为
| $\delta \left( i,\text{ }j \right)={{({{r}_{i}}-{{t}_{j}})}^{2}},$ | (2) |
则可建立两序列的匹配距离矩阵Dn×m:
| $\mathit{\boldsymbol{D}}{_{n \times m}} = \left[ {\begin{array}{*{20}{c}} {\delta \left( {1,{\rm{ }}1} \right)}& \ldots &{\delta \left( {1,{\rm{ }}m} \right)}\\ \ldots & \ddots & \ldots \\ {\delta \left( {n,{\rm{ }}1} \right)}&{ \ldots {\rm{ }}}&{\delta \left( {n,{\rm{ }}m} \right)} \end{array}} \right]{\rm{ }}。$ | (3) |
从中寻找一个路径P, 使得
| $P\left( R,\text{ }T \right)=\min \sum\limits_{\begin{smallmatrix} i\in \left( 1,\text{ }n \right) \\ \text{ }j\in \left( 1,\text{ }m \right) \end{smallmatrix}}{{}}\text{ }\delta \left( i,\text{ }j \right)。$ | (4) |
为使相似度具有意义, 路径P必须满足单调性要求, 即不得违背各序列元素的时间顺序:
| $P\left( {i,{\rm{ }}j} \right) = \min {\rm{ }}\left\{ \begin{array}{l} P\left( {i - 2,{\rm{ }}j - 1} \right){\rm{ }} + P\left( {i - 1,{\rm{ }}j} \right) + P\left( {i,{\rm{ }}j} \right)\\ P\left( {i - 1,{\rm{ }}j - 1} \right){\rm{ }} + P\left( {i,{\rm{ }}j} \right)\\ P\left( {i - 1,{\rm{ }}j - 2} \right){\rm{ }} + P\left( {i,{\rm{ }}j - 1} \right){\rm{ }} + P\left( {i,{\rm{ }}j} \right) \end{array} \right\}。$ | (5) |
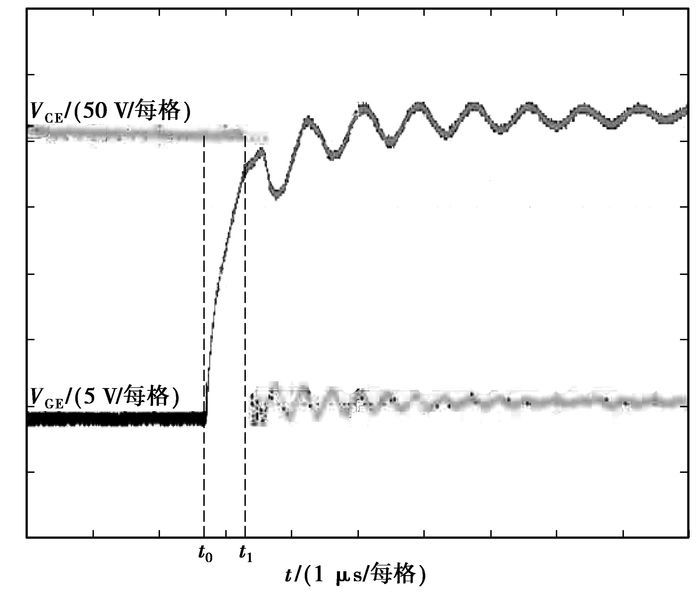
在IGBT模块门极电路的组成元素中, 门集电极之间的等效寄生电容CGC具有非线性特征, 随集射极电压VCE的变化而具有不同的值[30], 为避免参数非线性因素的影响, 需对门极电路进行线性化处理, 如图 3所示。
|
图 3 IGBT模块的开通波形 |
在门极电压VGE充电起始时刻t0至t1时刻集射极电压VCE开始下降, 因换流过程的存在, VCE将保持母线电压不变, 门集电极电容CGC≈CGDJ≤CGE[31], 由CGDJ的非线性造成的影响最小, 且瞬变电磁干扰尚未产生, 因此, 非常适合用来作为样本, 加之文献[27]已证实DTW算法具有很好的鲁棒性。因此, 笔者选择从t0~t1时段的门极电压VGE信号中挖掘隐含的缺陷信息。实现步骤如下:首先采集投运时, IGBT模块t0~t1时段的门极电压VGE作为参考样本序列R;然后, 按照一定周期采集不同运行阶段t0~t1时段的门极电压VGE作为检测样本序列T, 计算与参考样本序列R之间的DTW距离, 作为相似性度量, 判断IGBT模块内部是否存在缺陷。这里需要说明的是, 序列R和T的采样频率相同, 另外由于缺陷对门极电路元件参数的影响, 检测样本序列的维数可能与参考样本序列不一致, 而DTW算法却很好地克服了这个问题, 表现出很好的一致性。
采用DTW算法辨识IGBT模块缺陷的具体过程如下:
1) 根据公式(3) 计算序列R和T的匹配矩阵Dn×m。
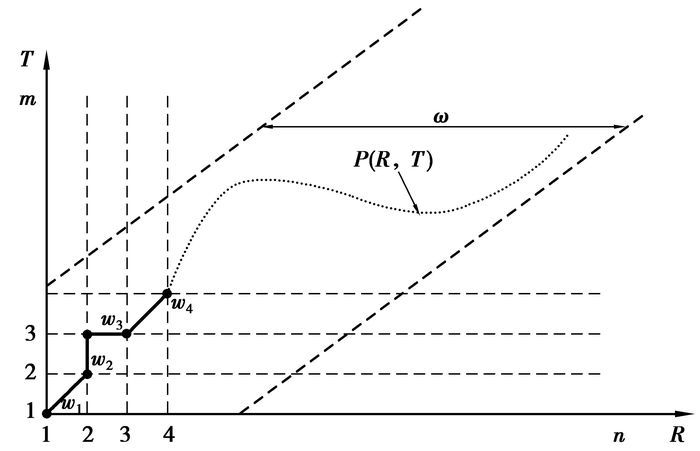
2) 将序列R和T投影到二维直角平面上, 如图 4所示, R在横轴上标出, T在纵轴上标出, 格点(i, j)表示元素ri和tj的交点。
|
图 4 缺陷辨识过程 |
3) 时间弯曲路径P则由平面中的一系列格点组成, P=∑wk, 其中wk对应于序列R中元素ri到序列T中元素tj的路径, 例如图 4中w3表示r2到t3的路径。序列R和T的DTW(R, T)=
4) 根据公式(5) 的单调性要求, 可以求出路径P的搜索限制条件:0≤ik-ik-1≤1;0≤jk-jk-1≤1;|ik-ik-1|≤ω=3。
5) 令γ(1, 1) =0, 然后从点(1, 1) 出发, 按照公式(6) 搜索路径P, 反复递推, 直至γ(n, m), 可得门极电压检测序列T与参考序列R的DTW(R, T), 根据DTW(R, T)的变化可辨识IGBT模块内部是否存在缺陷。
| $\begin{array}{l} \gamma \left( {i,{\rm{ }}j} \right) = {\rm{ }}\delta \left( {i,{\rm{ }}j} \right) + \min [\gamma \left( {i - 1,{\rm{ }}j} \right),\\ \quad \quad \quad \quad \gamma \left( {i - 1,{\rm{ }}j - 1} \right){\rm{ }},{\rm{ }}\gamma \left( {i,{\rm{ }}j - 1} \right)] \end{array}。$ | (6) |
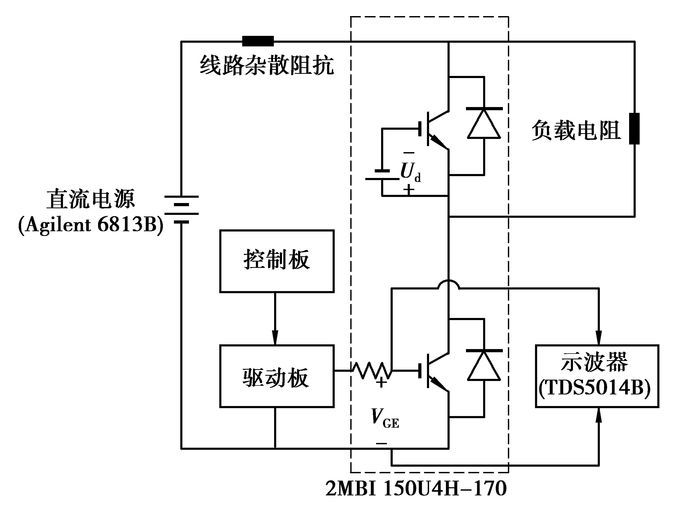
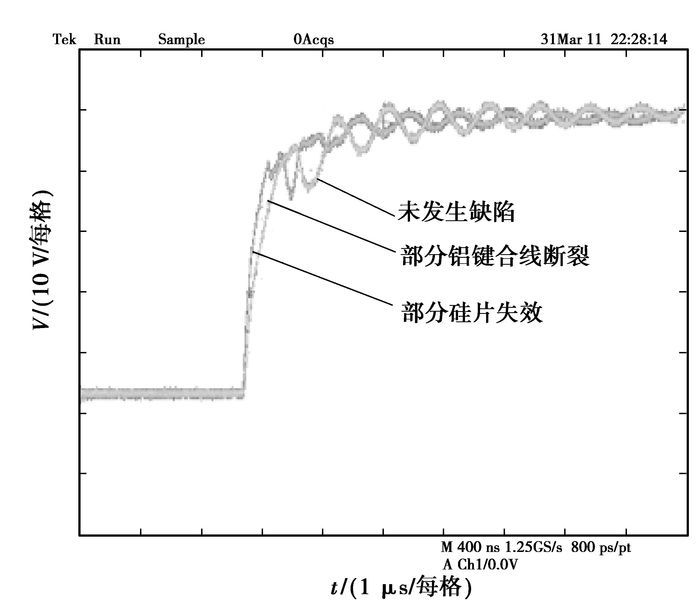
为验证上述方法的可行性, 笔者在实验室搭建了图 5所示IGBT模块动态特性测试电路, 其中实验样品采用由富士公司所提供的特殊开封IGBT模块-2MBI150U4H 170, 模拟现场运行中最易出现的铝键合线断裂缺陷。分两步进行, 首先模拟部分铝键合线断裂(3根), 研究寄生电阻元件和寄生电感元件对门极电压的影响;进而是部分硅片失效, 即联结IGBT器件中两并联硅片之一的铝键合线全部断裂(6根), 分析寄生电容对门极电压的影响。实验电路中, 输入电压:DC300 V, 负载:3 mH、1 Ω, 开关频率:10 kHz;示波器TDS5014B的采样频率为1.25 GHz, 测得的波形如图 6所示。从中可以看出, 部分铝键合线断裂时, 门极电压VGE的变化不明显;而部分硅片失效时, 门极电压VGE的变化非常明显。
|
图 5 实验电路示意图 |
|
图 6 缺陷前后门极电压的波形 |
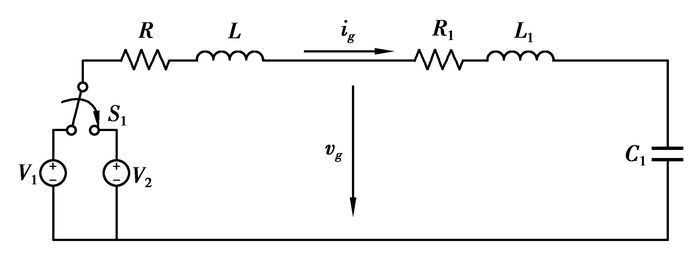
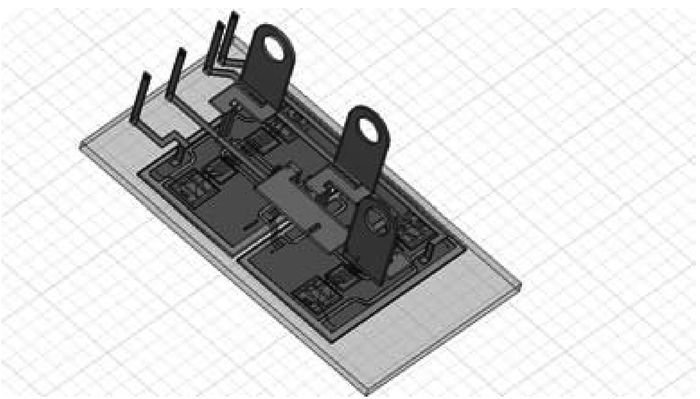
由2.2的分析可知在t0~t1时段IGBT模块门极寄生参数是常数, 驱动电路可由图 2简化为图 7所示的二阶电路。其中S1表示控制信号, V1和V2分别为正负驱动电压, R和L分别为外部等效电阻和电感, R1和L1分别为IGBT模块门极等效寄生电阻和电感, C1为IGBT模块门极等效电容。对于给定的驱动电路, V1、V2、R和L都是视为定值, 门极电压主要受R1、L1和C1的影响。为分析不同寄生参数的影响, 笔者利用Ansoft公司的Q3D Extractor软件建立了实验样品3D模型, 如图 8所示, 提取了上述寄生电阻和电感元件的参数:R=10.032 Ω, L=37 nH, R1=3.1 mΩ, L1=3 nH。从样品的数据手册得到C1≈Cies=14 nF。定义门极电压的动态变化J为
|
图 7 t0~t1时段门极等效电路 |
|
图 8 IGBT模块的3D模型 |
| $J({R_1},{\rm{ }}{L_1},{\rm{ }}{C_1}) = \sum\limits_{{\rm{ }}i = 1}^N {} {\rm{ }}{\left| {{v_{gb}}({t_i}) - {v_{ga}}({t_i})} \right|^2},$ | (7) |
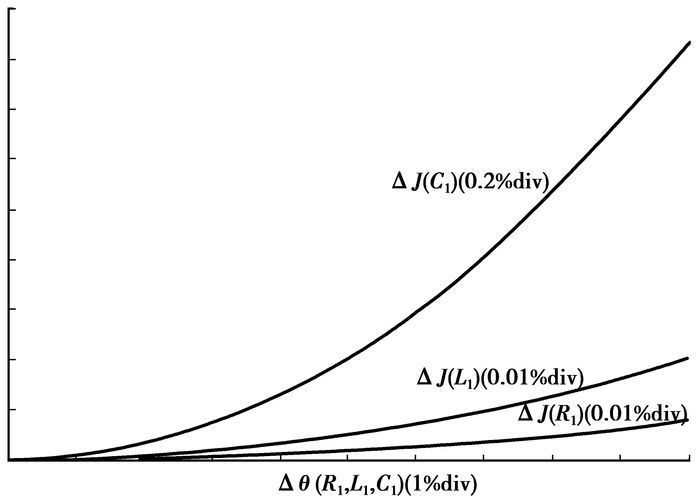
式中:vgb和vga为寄生参数变化前后的门极电压;N为t0~t1时段的采样点数, 则J对R1、L1和C1的灵敏度分析如图 9所示。从中可以看出寄生电容对门极电压VGE波形变化起决定作用, 这与实验结果相吻合。
|
图 9 寄生参数对门极电压的影响 |
提取图 6所示未发生缺陷时的IGBT门极电压信号中t0-t1时段数据, 作为参考序列R, 并重复测量未发生缺陷时的IGBT门极电压信号, 按照相同的方法提取t0-t1时段数据作为良好状态的测量序列T1, 然后按照同样的方法提取部分铝键合线断裂状态的测量序列T2和部分硅片失效状态的测量序列T3, 再按照2.2中DTW的计算方法, 可获得不同缺陷状态下门极电压测量序列同参考序列之间的DTW计算结果, 如表 1所示。从中可以看出, 部分铝键合线断裂时, 序列T与R的DTW为0.93;部分硅片失效时, 序列T与R的DTW为78.27;而未发生缺陷时, 序列T与R的DTW为0.01;显然, 门极电压VGE在t0~t1时段的信号序列DTW变化可作为参数诊断IGBT模块内部是否存在缺陷:当观测的门极电压VGE在t0~t1时段的序列DTW发生细微变化时, 应加强对门极电压VGE的监测, 若此后的监测数据显示, 其相似度变化呈增大趋势, 并且在达到一定数值(比如10, ≫误差)之后, 仍然在继续增长, 即可排除测量误差或其他干扰因素的影响, 判定IGBT模块内部出现缺陷, 可考虑停机将该IGBT模块替换掉。
| 表 1 门极杂散参数估计结果 |
笔者提出一种基于时间序列DTW的IGBT模块早期缺陷的诊断方法, 并通过实验证实了该方法的正确性。结果表明, 该方法能够有效诊断出IGBT模块内部的缺陷, 相对于已有的电力电子装置故障诊断方法, 可为运行人员赢得宽裕的维护时间, 及时替换有缺陷的IGBT模块, 避免模块故障及对装置造成的危害。同时该方法对采集速度和精度要求高, 尚需进一步完善。
| [1] | 汤广富, 刘文华. 提高电网可靠性的大功率电力电子技术基础理论[M]. 北京: 清华大学出版社, 2010. |
| [2] | Bryant A, Yang Shaoyong, Mawby P, et al. Investigation into IGBT dV/dt during turn-off and its temperature dependence[J]. IEEE Transactions on Power Electronic, 2011, 26(10): 3019–3031. DOI:10.1109/TPEL.2011.2125803 |
| [3] | Yang S Y, Xiang D W, Bryant A, et al. Condition monitoring for device reliability in power electronic converters:a review[J]. IEEE Transactions on Power Electronic, 2010, 25(11): 2734–2752. DOI:10.1109/TPEL.2010.2049377 |
| [4] | Rashid M H. Power electronics:circuits, devices, and applications[M]. 3rd ed. NJ: Prentice Hall, 2004. |
| [5] | Chen Z, Guerrero J M, Blaabjerg F. A review of the state of the art of power electronics for wind turbines[J]. IEEE Transactions on Power Electronic, 2009, 24(8): 1859–1875. DOI:10.1109/TPEL.2009.2017082 |
| [6] | Ciappa M. Selected failure mechanisms of modern power modules[J]. Microelectronics Reliability, 2002, 42(4/5): 653–667. |
| [7] | Patil N, Celaya J, Das D, et al. Precursor parameter identification for insulated gate bipolar transistor (IGBT) prognostics[J]. IEEE Transactions on Reliability, 2009, 58(2): 271–276. DOI:10.1109/TR.2009.2020134 |
| [8] |
赵争鸣, 张海涛, 袁立强, 等基于IGCT的高压三电平变频器失效机理及保护策略[J].电工技术学报, 2006, 21(5):1-6, 18. ZHAO Zhengming, ZHANG Haitao, YUAN Liqiang, et al. Failure mechanism and protection strategy of high voltage three-level inverter based on IGCT[J]. 2006, 21(5):1-6, 18. http://d.wanfangdata.com.cn/Conference/7085765 |
| [9] |
马伟明, 胡安, 王令蓉.
基于电压波形分析的十二相整流装置故障诊断[J]. 电工技术学报, 1997, 12(6): 49–54.
MA Weiming, HU An, WANG Lingrong. Twelve-phase rectifier fault diagnosis based on voltage waveform analysis[J]. Transactions of China Electrotechnical Society, 1997, 12(6): 49–54. (in Chinese) |
| [10] |
李薇, 谭阳红, 彭永进.
基于小波分析及网络的电力电子电路故障诊断方法[J]. 电机与控制学报, 2005, 9(6): 555–561.
LI Wei, TAN Yanghong, PENG Yongjin. Fault diagnosis methods of power electronic circuits based on wavelet analysis and network[J]. Electric Machines and Control, 2005, 9(6): 555–561. (in Chinese) |
| [11] |
罗慧, 王友仁, 崔江, 等.
电力电子电路多源特征层融合故障诊断方法[J]. 电机与控制学报, 2010, 14(4): 92–96.
LUO Hui, WANG Youren, CUI Jiang, et al. Intelligent fault diagnosis for power electronic circuits based on multi-source feature-level fusion[J]. Electric Machines and Control, 2010, 14(4): 92–96. (in Chinese) |
| [12] |
丘东元, 彭锦凤, 张波.
电力电子变换器结构性故障的有向图论诊断方法[J]. 电机与控制学报, 2010, 14(8): 13–18.
QIU Dongyuan, PENG Jinfeng, ZHANG Bo. Structural fault diagnosis method of power electronic converter by directed graph theory[J]. Electric Machines and Control, 2010, 14(8): 13–18. (in Chinese) |
| [13] |
陈如清.
采用新型粒子群算法的电力电子装置在线故障诊断方法[J]. 中国电机工程学报, 2008, 28(24): 70–74.
CHEN Ruqing. A novel PSO on-line fault diagnosis approach for power electronic system[J]. Proceedings of the Chinese Society for Electrical Engineering, 2008, 28(24): 70–74. DOI:10.3321/j.issn:0258-8013.2008.24.012 (in Chinese) |
| [14] |
胡清, 王荣杰, 詹宜巨.
基于支持向量机的电力电子电路故障诊断技术[J]. 中国电机工程学报, 2008, 28(12): 107–111.
HU Qing, WANG Rongjie, ZHAN Yiju. Fault diagnosis technology based on SVM in power electronic circuit[J]. Proceeding of the Chinese Society for Electrical Engineering, 2008, 28(12): 107–111. DOI:10.3321/j.issn:0258-8013.2008.12.018 (in Chinese) |
| [15] |
张志学, 马皓, 毛兴云.
基于混杂系统模型和事件辨识的电力电子电路故障诊断[J]. 中国电机工程学报, 2005, 25(3): 49–53.
ZHANG Zhixue, MA Hao, MAO xingyun. Fault diagnosis for power electronic circuits based on hybrid system theory and event identification[J]. Proceedings of the Chinese Society for Electrical Engineering, 2005, 25(3): 49–53. (in Chinese) |
| [16] | Xiong Y L, Xiong Y L, Cheng X, et al. Prognostic and warning system for power-electronic modules in electric, hybrid electric, and fuel-cell vehicles[J]. IEEE Transactions on Industrial Electronics, 2008, 55(6): 2268–2276. DOI:10.1109/TIE.2008.918399 |
| [17] | Xiang D W, Ran L, Tavner P, et al. Monitoring solder fatigue in a power module using case-above-ambient temperature rise[J]. IEEE Transactions on Industry Applications, 2011, 47(6): 2578–2591. DOI:10.1109/TIA.2011.2168556 |
| [18] | Anderson J M, Cox R W. On-line condition monitoring for MOSFET and IGBT switches in digitally controlled drives[C]//Proceedinga of Energy Conversion Congress and Exposition (ECCE), September 17-22, 2011, Phoenix, Arizona. Piscataway:IEEE Presss, 2011:3920-3927. |
| [19] | Saha B, Celaya J R, Wysocki P F, et al. Towards prognostics for electronics components[C]//Proceedings of Aerospace Conference, Marchi 7-14, 2009, Big Sky, Montana. Piscataway:IEEE Press, 2009:1-7. |
| [20] | Sheng W W, Colino R P. Power electronic modules:design and manufacture[M]. Boca Raton: CRC Press, 2004. |
| [21] | Mohan N, Undeland T M. Power electronics:converters, applications, and design[M]. 3rd ed. New York: Wiley, 2007. |
| [22] | Yu C Z, Yuan J S, Yang H. MOSFET linearity performance degradation subject to drain and gate voltage stress[J]. IEEE Transactions on Device and Materials Reliability, 2004, 4(4): 681–689. DOI:10.1109/TDMR.2004.838407 |
| [23] | Tang M C, Fang Y K, Liao W S, et al. Investigation and modeling of hot carrier effects on performance of 45-and 55-nm NMOSFETs with RF automatic measurement[J]. IEEE Transactions on Electron Devices, 2008, 55(6): 1541–1546. DOI:10.1109/TED.2008.921998 |
| [24] | Xing K, Lee F C, Boroyevich D. Extraction of parasitics within wire-bond IGBT modules[C]//Proceedings of Applied Power Electronics Conference and Exposition, February 15-19, 1998, Anaheim, CA, USA. Piscataway:IEEE Press, 1998, 1:497-503. |
| [25] | Martin C, Schanen J L, Guichon J M, et al. Analysis of electromagnetic coupling and current distribution inside a power module[J]. IEEE Transactions on Industry Applications, 2007, 43(4): 893–901. DOI:10.1109/TIA.2007.900453 |
| [26] |
徐波, 唐海龙, 李行善.
基于DTW的涡扇发动机气路故障定量诊断方法[J]. 北京航空航天大学学报, 2004, 30(6): 524–528.
XU Bo, TANG Hailong, LI Xingshan. DTW based quantitative fault diagnosis of gas path component in turbofan[J]. Journal of Beijing University of Aeronautics Astronautics, 2004, 30(6): 524–528. (in Chinese) |
| [27] |
牛征, 牛玉广, 刘吉殝, 等.
基于动态时间归整技术的电站过程故障诊断方法[J]. 动力工程, 2006, 26(3): 396–399.
NIU Zheng, NIU Yuguang, LIU Jizhen, et al. Fault diagnosis of processes in power plants based on dynamic time warping[J]. Journal of Power Engineering, 2006, 26(3): 396–399. (in Chinese) |
| [28] |
王振浩, 杜凌艳, 李国庆, 等.
动态时间规整算法诊断高压断路器故障[J]. 高电压技术, 2006, 32(10): 36–38.
WANG Zhenhao, DU Lingyan, LI Guoqing, et al. Fault diagnosis of high voltage circuit breakers based on dynamic time warping algorithm[J]. High Voltage Engineering, 2006, 32(10): 36–38. DOI:10.3969/j.issn.1003-6520.2006.10.011 (in Chinese) |
| [29] | Berndt D, Berndt, Clifford J. Using dynamic time warping to find patterns in time series[R].[S.l.]:AAAI, 1994. |
| [30] | Hefner A R, Diebolt D M. An experimentally verified IGBT model implemented in saber circuit simulator[J]. IEEE Transactions on Power Electronic, 1994, 9(5): 532–542. DOI:10.1109/63.321038 |
| [31] |
唐勇, 胡安, 陈明.
IGBT栅极特性与参数提取[J]. 电工技术学报, 2009, 24(7): 76–80.
TANG Yong, HU An, CHEN Ming. IGBT gate characteristics and parameter extraction methods[J]. Transactions of China Electrotechnical Society, 2009, 24(7): 76–80. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


