喷嘴喷雾冷却在冶金行业中应用十分广泛, 从炼焦、烧结矿的冷却到高炉废气冷却、连铸坯喷雾二次冷却、轧钢过程中的控制冷却、表面除鳞均需要采用喷嘴喷雾冷却。喷嘴喷雾冷却特性的优劣, 与冶金过程生产质量、生产效率密切相关。影响喷嘴冷却特性的因素很多, 喷嘴的结构设计、加工精度是决定性因素, 但在喷嘴的使用过程中, 因使用温度、冷却介质中的杂质、磨损、机械碰撞等因素均可能造成喷嘴性能失效。因此, 对喷嘴特性进行准确的测试, 保证实际生产中所使用喷嘴的性能达到设计要求, 对冶金生产过程十分重要。喷雾冷却性能通常以传热系数来评价其冷却效率, 传热系数越大, 喷嘴冷却效率就越高[1]。关于表面传热系数测定方法的研究, 国内外开展了相关研究。Wendelstorf[2]等人通过热传导过程的数学模型, 研究了喷雾冷却中热传导系数的决定因素以及影响表面热量散失的因素。郑忠[3-4]等对板坯连铸机所使用的常见喷嘴进行了冷态和热态性能的测定, 并获得了水流密度和传热系数的函数关系式。Hernandez[5-6]等人针对连铸二冷过程, 用PIV对气/水雾化喷嘴流场进行了测试研究, 给出了气雾颗粒直径的临界范围, 指出在该尺度范围所形成的气雾和低于该尺度所形成的微颗粒流场的特性, 研究了水流密度、水气比等因素对射流的影响。笔者综合前人的研究成果, 提出基于多段拟合的表面传热系数测试方法并开发了相应的装置, 并通过试验装置测试了在不同温度、水流密度、喷水压力下的表面传热系数, 为喷嘴出厂质量检验、喷嘴结构优化以及喷嘴的冷却效果提供测试平台。
1 实验原理和方法 1.1 实验原理冷却雾喷射到带钢表面, 带钢试件表面温度降低并形成内外温度较大的温度梯度, 使带钢内部热量沿着垂直表面的方向传出。从喷嘴冷却的局部看, 带钢试件近似于一维传热。因此在测定传热系数过程中, 模拟试件传热也应近似于一维传热。假定试件在传热过程中无内热源, 其一维热传导方程为
| ${{C}_{p}}\rho \frac{\partial T\left( x,\text{ }t \right)}{\partial t}=\frac{\partial }{\partial x}\left( \lambda \frac{\partial T\left( x,\text{ }t \right)}{\partial x} \right),$ | (1) |
式中:Cp为热容量;ρ为密度;λ为导热系数。
由于带钢的导热系数随温度的变化关系成直线关系:
| $\lambda =a+bT。$ | (2) |
则(1) 式变为
| ${{C}_{p}}\rho \frac{\partial T\left( x,\text{ }t \right)}{\partial t}=\lambda \frac{{{\partial }^{2}}T\left( x,\text{ }t \right)}{\partial {{x}^{2}}}+b{{\left( \frac{\partial T\left( x,\text{ }t \right)}{\partial x} \right)}^{2}}。$ | (3) |
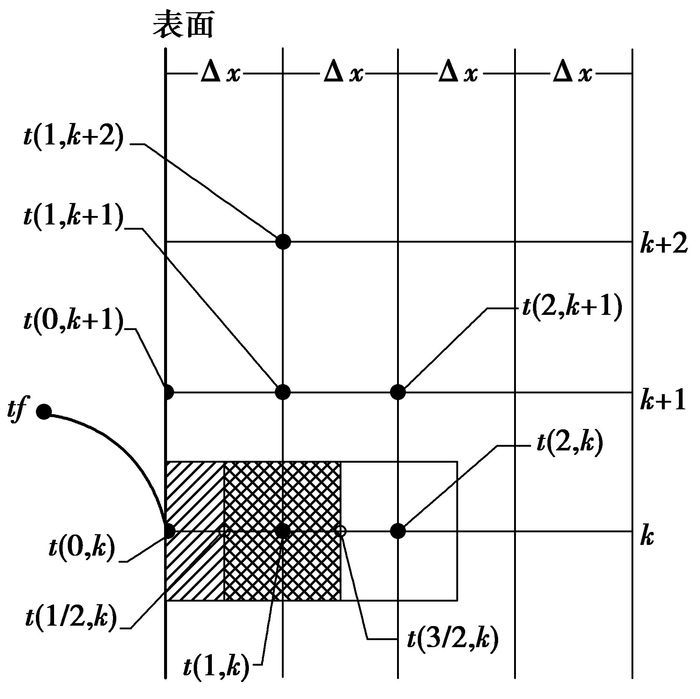
用差分法求解式(3), 离散化网格划分如图 1所示。
|
图 1 差分网格划分示意图 |
差分后得到内部节点的差分方程为
| $\begin{matrix} {{C}_{p}}\rho \frac{t\left( i,\text{ }k+1 \right)\text{ }-t\left( i,\text{ }k \right)}{\Delta \tau }= \\ \lambda \frac{t\left( i+1,\text{ }k \right)-2t\left( i,\text{ }k \right)+t\left( i-1,\text{ }k \right)}{{{\left( \Delta x \right)}^{2}}}+ \\ \frac{b({{\left( t\left( i+1,\text{ }k \right)-t\left( i,\text{ }k \right) \right)}^{2}})}{{{\left( \Delta x \right)}^{2}}}。\\ \end{matrix}$ | (4) |
测试开始时试样的温度为已知, 初始条件为:T(x, t)|t=0=T(x, 0), 测试过程中, 试样冷却表面的边界温度可用热电偶测出, 其边界条件为
| $T\left( x,\text{ }t \right){{|}_{x=L}}=T\left( L,\text{ }t \right),$ | (5) |
| $\lambda \frac{\partial T\left( x,\text{ }t \right)}{\partial x}{{|}_{x=0}}=h\left[ T\left( x,\text{ }0 \right)-tf \right],$ | (6) |
差分方程的稳定性条件为
| $\frac{\Delta \tau \cdot \lambda }{{{C}_{p}}\rho {{\left( \Delta x \right)}^{2}}}\le \frac{1}{2}。$ | (7) |
实际测量时, 空间步长Δx取20 mm, 时间步长Δτ取0.5 s, 不管试样钢种的热物性参数如何, 均能满足稳定性条件式的要求。测量过程中, 测定了带钢试样按网格划分的不同时刻t(1, k)和t(2, k)两节点温度值, 则表面温度t(0, k)和传热系数可分别由差分方程进行计算。
1.2 实验方法及装置实验研究喷嘴与表面传热系数的方法有稳态法和非稳态法, 由于稳态法对试样加工要求较高, 且试样的温度较难控制, 因此采用非稳态法测定表面传热系数。在被测试样内部不同点处布置一系列测温点, 埋入K分度热电偶, 通过PLC S7-200热电偶采集模块实时采集各点的温度, 采样频率为2 Hz。从而计算出钢带试件测试表面点的传热系数, 通过系列点的传热系数计算综合传热系数。实验装置主要由电阻炉、电阻炉加热器、供水供气装置、PLC数据采集及控制系统组成。实验装置如图 2所示。

|
图 2 实验装置示意图 |
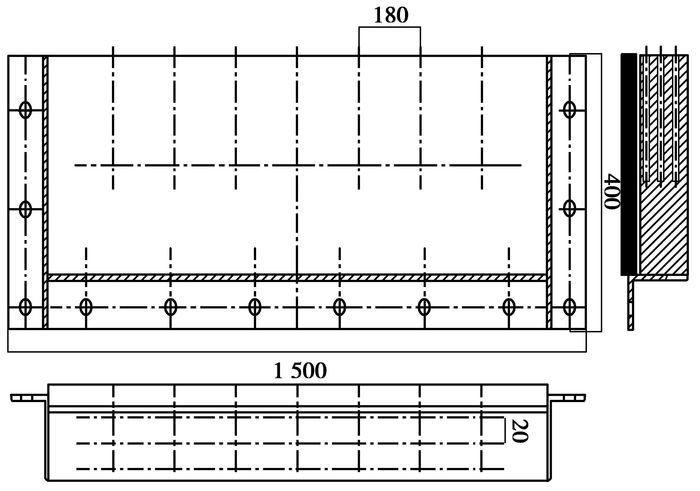
测试台采用Q215钢种。考虑设计的测试平台为通用喷嘴的测试平台及加热的需要, 安装预留100 mm×30 mm用于加热炉安装定位, 试样尺寸确定为1 550 mm×400 mm×80 mm。在1 500 mm的长度中心线方向每间距180mm依次安装7支热电偶, 在80 mm的钢带高度方向每隔20mm安装3支热电偶, 共安装21支K分度热电偶。实验测试用钢板尺寸及热电偶的布置示意图如图 3所示。
|
图 3 温度测点布置图 |
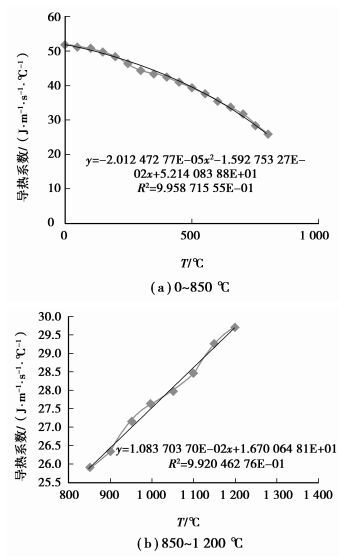
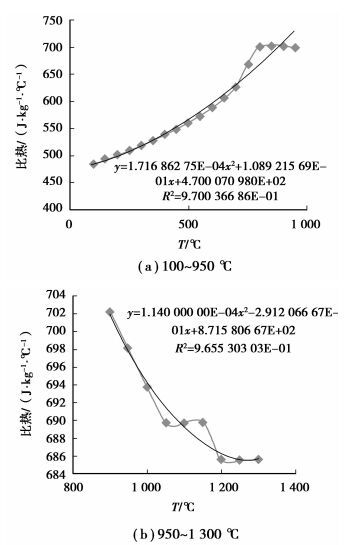
在离散化求解过程中, 试样(Q215) 的密度、导热系数、比热与温度的关系采用分段拟合方程, 以下为其相应的变化曲线及方程, 如图 4~6所示。

|
图 4 Q215密度与温度的关系 |
|
图 5 Q215导热系数与温度的关系 |
|
图 6 Q215比热容与温度的关系 |
图 7给出了不同压力条件下, 试样在加热到850 ℃后喷水冷却传热系数与表面温度之间的变化关系, 实验条件是喷嘴距试样200 mm, 水流密度为4.0 L/(m2·s), 喷气压力不变为0.4 MPa, 喷水压力依次为0.2, 0.4, 0.6 MPa。表面温度与传热系数的关系曲线如图 7所示。

|
图 7 不同压力下表面温度与传热系数关系 |
由上图可以看出, 喷嘴在对Q215表面进行冷却时, 表面温度对传热系数影响很大, 总体规律是表面温度越高, 传热系数越小。在高温区, 传热系数非常小, 这是稳定膜状沸腾区域, 喷嘴喷出的水滴在表面容易气化形成水蒸气层, 水滴没有完全渗透表面, 阻止了表面的传热。当温度下降时, 由于表面的沸腾, 热传导机理发生改变, 传热系数逐渐增大。当表面温度约在600 ℃, 低于该温度传热系数值快速上升, 大于此温度传热系数值变化平缓, 该临界温度就是人们常说的Leidenfrost温度。
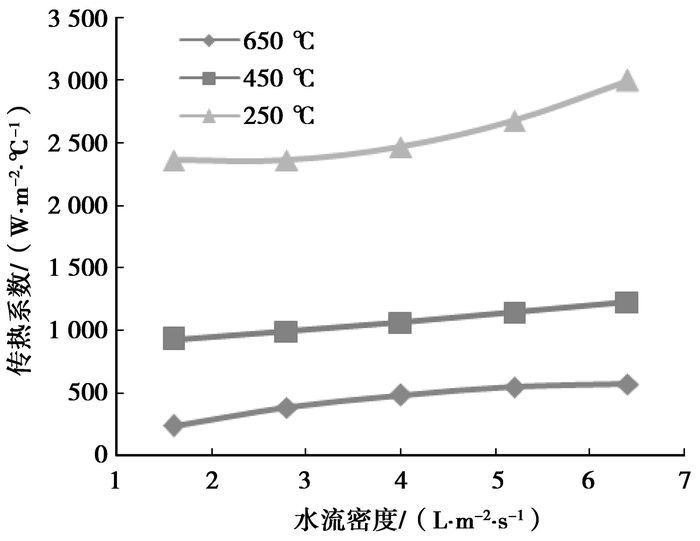
2.2 水流密度对传热系数的影响喷嘴的水流密度即单位时间、单位面积试样表面的喷水量。水流密度与传热系数有密切的关系, 喷嘴的压力特性、体积流量、喷嘴距试样表面的距离均能归结为水流密度的影响。图 8给出不同表面温度条件下, 喷嘴水流密度与传热系数的关系。实验条件是喷嘴距试样200 mm, 如图 2所示。
|
图 8 不同表面温度下水流密度与传热系数关系 |
图 8给出了不同表面温度下流量密度对传热系数的影响关系, 从测试结果看, 不管表面温度高低, 水流密度增加, 由其带走的热量增加, 传热系数呈上升趋势;同一水流密度条件下, 随着表面温度的降低, 传热系数逐渐增加;在低温区随着喷嘴水流密度的增大, 传热系数增加的幅度较高温区大。
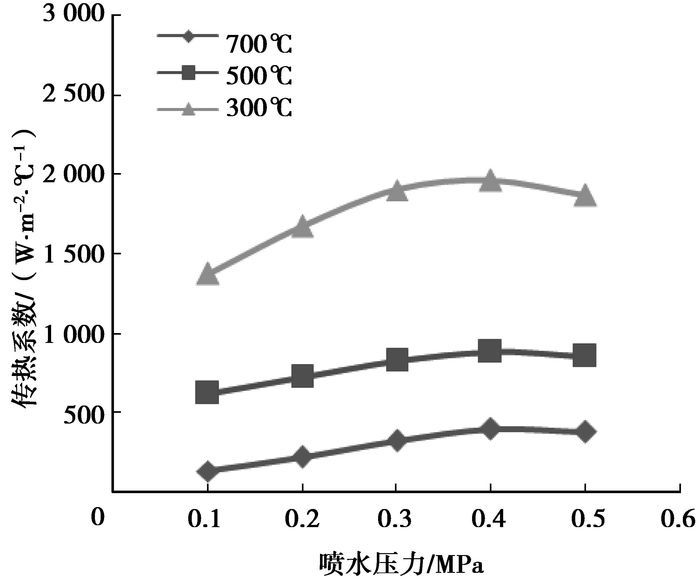
2.3 喷水压力对传热系数的影响图 9给出了表面温度不同时, 水气喷嘴冷却时传热系数与喷嘴前水压力的关系, 图中在改变喷嘴前水压力时, 空气压力保持基本不变(0.4 MPa), 水气比随喷嘴前水压力的改变而变化, 喷嘴距表面距离为200 mm。
|
图 9 不同表面温度下喷水压力与传热系数关系 |
喷嘴的喷水压力(水气比)对传热系数的影响, 总的趋势是随喷嘴的喷水压力(水气比)增大, 传热系数增大。从图 9还可看出, 表面温度对这种趋势有较大影响, 在高温区, 喷水压力(水气比)增大, 传热系数增加缓慢, 在低温区, 增加要快些。但当喷嘴的喷水压力增加到一定值后效果会变差, 说明在水气喷嘴对表面进行冷却时有一个合适的水压, 即水气比, 这是由于当水气比增加到一定值后, 由于水滴尺寸过小, 导致微小水滴产生漂移, 会使冲击强度减小, 减弱了水滴对表面的冷却作用, 从而使传热系数减小。因此, 存在最佳水气比和最佳粒径范围问题。根据前人研究, 结果表明水气喷嘴的最佳粒径范围为:20~80 μm。从测试结果来看, 水气喷嘴喷水压力控制在0.40 MPa左右较为合适, 在工作水量条件下能保证喷雾水滴的粒径在20~80 μm范围内。
3 结语采用非稳态一维导热微分方程, 在线采集试件不同测点在冷却过程中的温度变化, 离线拟合分析测点温度与时间的拟合方程, 结合密度、比热容及导热系数等热物性参数与温度拟合方程, 对非稳态导热方程进行离散处理可间接测量表面的传热系数, 进而评价喷嘴冷却特性。现场测试实验结果表明, 该方法可行, 能实现喷嘴冷却特性测试及喷嘴性能评价。
| [1] | 张亚竹, 华祺年, 赵增武, 等. 连铸二冷气水雾化喷嘴冷态特性研究[C]//第十六届全国炼钢学术会议论文集, 1, Nov. , 2010, 北京, 中国. 北京: 中国金属学会, 2010(12): 409-414. |
| [2] | Wendelstorf J, Spitzer K H, Wedelstorf R. Spray water cooling heat transfer at high temperatures and liquid mass fluxes[J]. International Journal of Heat and Mass Transfer, 2008, 51(19/20): 4902–491. |
| [3] |
文光华, 唐萍, 韩志伟, 等.
连铸二冷喷嘴传热系数的实验研究[J]. 中国金属学会能源与热工2002学术年会, 2002(9): 537–541.
WEN Guanghua, TANG Ping, HAN Zhiwei, et al. Experimental study on heat transfer coefficient of nozzle in secondary cooling zone[J]. The 2002 Academic Annual Conference of Thermal Energy and Heat Engineering Branch of Chinese Metal Association, 2002(9): 537–541. (in Chinese) |
| [4] |
郑忠, 刘兵, 罗小刚.
攀钢板坯连铸二冷喷嘴性能的热态实验研究[J]. 工业加热, 2008, 37(4): 11–15.
ZHENG Zhong, LIU Bing, LUO Xiaogang. The hot state test study on nozzle's character in secondary water Cooling zone of slab continuous casting in pan steel[J]. Industrial Heating, 2008, 37(4): 11–15. (in Chinese) |
| [5] | Hernandez I C, Acosta F A, Castillejos A H E, et al. The fluid dynamics of secondary cooling air-mist jets[J]. Metallurgical and Materials Transactions B, 2008, 39(5): 746–763. DOI:10.1007/s11663-008-9179-x |
| [6] | Sengupta J, Thomas B G, Wells M A. Understand the role water-cooling plays during continuous casting Steel and Aluminum Allays[C]. MS & T 2004 Conference Proceedings, 2004:179-193. |
| [7] |
陈东芳, 唐大伟, 胡学功.
流量、换热表面方向对光滑表面喷雾冷却的影响[J]. 工程热物理学报, 2010(7): 1167–1170.
CHEN Dongfang, TANG Dawei, HU Xuegong. Effect of flow rate and pate and plain surface orientation on spray cooling[J]. Journal of Engineering Thermophysics, 2010(7): 1167–1170. (in Chinese) |
| [8] | StewarT I, Massingham J D, Hagers J J. Heat transfer coefficient effects on spray cooling[J]. Iron and Steel Engineer, 1996, 73(7): 17–23. |
| [9] | Klinzing W P, Rozzi J C, Mudawar I. Film and transition boiling correlations for quenching of hot surfaces with water spray[J]. Journal of Heat Treating, 1992, 9(2): 91–103. DOI:10.1007/BF02833145 |
| [10] | Ciofalo M, Piazza I D, Brucato V. Investigation of the cooling of hot walls by liquid waters sprays[J]. International Journal of Heat and Mass Transfer, 1999, 42(7): 1157–1175. DOI:10.1016/S0017-9310(98)00250-6 |
| [11] |
梅国晖, 孟红记, 武荣阳, 等.
高温表面喷雾冷却传热系数的理论分析[J]. 冶金能源, 2004, 23(3): 18–30.
MEI Guohui, MENG Hongji, WU Rongyang, et al. Analysis of spray cooling heat transfer coefficient on high temperature surface[J]. Energy For Metallurgical Industry, 2004, 23(3): 18–30. (in Chinese) |
| [12] | Oliveira M S A, Sousa A C M. Neural network analysis of experimental data for air/water spray cooling[J]. Journal of Materials Processing Technology, 2001, 113(1/2/3): 439–445. |
| [13] | Choi K J, Yao S C. Mechanisms of film boiling heat transfer of normally impacting spray[J]. International Journal of Heat Mass Transfer, 1987, 30(2): 311–318. DOI:10.1016/0017-9310(87)90119-0 |
 2013, Vol. 36
2013, Vol. 36

