b. 重庆大学 国家镁合金材料工程技术研究中心, 重庆 400044
b. National Engineering Research Center for Magnesium Alloys, Chongqing University, Chongqing 400044, China
镁及绝大多数镁合金都具有密排六方结构,滑移系少,成形困难,因而镁合金主要采用铸造或压铸工艺生产,但变形镁合金较铸造镁合金具有更高的强度,更优异的力学性能,可满足更多样化的结构件要求,因而备受研究者青睐。AZ31镁合金是目前应用较为广泛的变形镁合金,具有良好的塑性变形能力和中等强度且价格便宜,但其也存在着室温塑性差,变形能力不足等缺陷[1]。为了扩大AZ31变形镁合金在工业上的应用范围,许多研究者对此开展了大量的研究工作,并发现Sr和Y可以有效改善AZ31的组织和性能。潘复生等人[2-3]研究发现,Sr的加入除可有效细化AZ31晶粒外,还可以有效改善Mg17Al12的形态和分布,并形成新的层片状离异共晶相;同时也研究了Y对挤压态AZ31镁合金组织和性能的影响。陈刚等人[4]研究发现Sr和Y同时加入AZ31中,可有效降低AZ31的腐蚀电流密度和腐蚀速率,从而使其腐蚀性能提高。Alireza Sadeghi[5]研究了微量的Sr对AZ31挤压过程中组织与织构的影响。尽管如此,人们对Sr和Y在AZ31中的作用研究仅仅局限在合金的高温性能、蠕变性能以及腐蚀性能等方面,而对添加Sr和Y后的高温流变行为研究甚少[2-4]。为此,笔者在变形温度为250~450 ℃和应变速率为0.01~1 s-1条件下研究合金的流变应力与变形温度和应变速度之间的关系,建立了合金流变过程的本构方程和塑性加工图,并结合金相显微组织观察,对塑性加工图进行分析,从而得出材料合理的热加工区,以期为实际生产中确定该合金的热加工工艺提供理论参考。
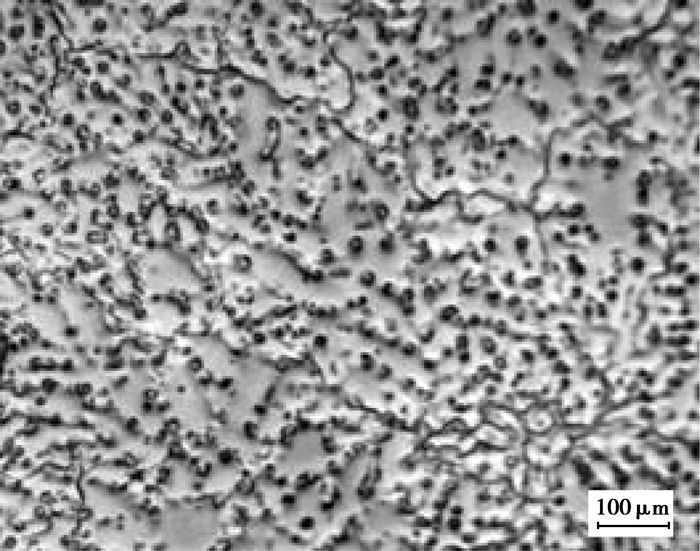
1 实验方法实验原材料为Mg-10Sr中间合金、Mg-30Y中间合金和商用铸造AZ31镁合金。将AZ31镁合金放置于电阻熔炼炉中的石墨坩埚内,充氩气保护,加热至720 ℃使其全部熔化后,静置保温10 min,再加入一定质量的Mg-10Sr中间合金和Mg-30Y中间合金,保温30 min,待温度降低至680 ℃左右,用金属模具浇注成ø90 mm×30 mm的铸锭。等离子吸收光谱法分析合金的实际成分如表 1所示。合金在390 ℃×16 h下均匀化退火后沿轴向截取ø10 mm×12 mm的圆柱试样,在Gleeble1500D热模拟试验机上进行热压缩实验,实验温度为250,300,350,400,450 ℃;应变速率为0.01,0.1,1 s-1;应变量为0.8;为了减少压缩过程中试样端部所受摩擦力,实验前在试样两端涂抹石墨做润滑剂;试样加热速度为5 ℃/s,到达预定温度后保温3 min进行压缩,压缩完后立即水淬以保留变形组织。截取均匀化后的铸态试样和热压缩后的试样,试样经过打磨、抛光和3%的硝酸酒精腐蚀后,在金相显微镜下对其组织进行观察。铸态AZ31-0.5Sr-1.5Y试样的显微组织如图 1所示。由图 1可知,向AZ31中复合添加Sr和Y可以有效细化组织,其组织仍然保持一定的铸态组织特征,晶界处短杆状的Al4Sr相和晶内颗粒状的Al2Y相分布较为均匀[4]。
|
图 1 铸态AZ31-0.5Sr-1.5Y合金金相显微组织 |
| 表 1 试验用合金的主要化学成分 |
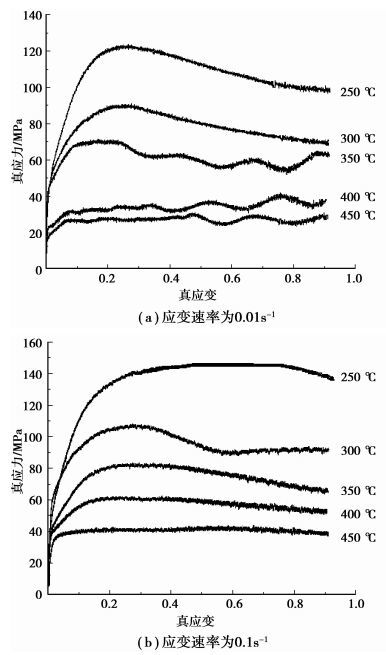
AZ31-0.5Sr-1.5Y在热压缩过程中典型的应力应变曲线如图 2所示。可以看出实验合金热压缩时的总体变化规律为:首先在微变形阶段,由于加工硬化占主导,随着应变的增加应力急剧增加;随着变形的继续,位错密度不断增加,由动态回复和动态再结晶所引起的软化作用逐渐增加,流变曲线开始变得平缓;当达到某一临界应变量时,由动态再结晶所引起的软化速率大于加工硬化速率,流变曲线达到峰值后便逐渐下降,最后保持某一稳定值,即进入稳态流动阶段。值得指出的是在高温低应变速率条件下,当应变量较小时,流变应力就保持不变即进入稳态流变阶段(如图 1(a)中的400 ℃和450 ℃),这可能是由于高温低应变速率时,原子热运动能量增加,扩散加剧,位错攀移和交滑移更易于进行,动态回复和动态再结晶加剧所致[6]。其次应变速率一定时,随着温度的增加,流变应力降低,峰值应力与稳态流变应力之间的差值减小,峰值应力所对应的应变左移。这可能是因为随着温度升高,镁合金中可开动的滑移系数目增加,滑移所需临界切应力下降,形变抗力也随之下降;温度越高动态回复和动态再结晶也越易发生,从而致使峰值应力提前[7]。最后当温度一定时,随着应变速率的增加,流变应力增加,即材料表现出正的应变速率敏感性。
|
图 2 AZ31-0.5Sr-1.5Y镁合金的真应力应变曲线图 |
本构方程是用来描述合金在热变形过程中流变应力与变形温度和变形速率之间的关系式,主要有适用于低应力水平的指数关系式,适用于较高应力水平的幂指数关系式和适用于所有应力水平的双曲正弦函数关系式,其表达式[8-10]分别为
| $ \dot \varepsilon = {A_1}{\sigma ^{{n_1}}}\exp \left( { - \frac{Q}{{RT}}} \right), $ | (1) |
| $ \dot \varepsilon = {A_2}\exp \left( {\beta \sigma } \right)\exp \left( { - \frac{Q}{{RT}}} \right), $ | (2) |
| $ \dot \varepsilon = A{\left[ {\sinh \left( {\alpha \sigma } \right)} \right]^n}\exp \left( { - \frac{Q}{{RT}}} \right), $ | (3) |
式中:A1,A2,A,α,β,n1为常数;n为加工硬化指数;Q为材料热变形难易程度的应变激活能;并且有
| $ \ln \dot \varepsilon = {n_1}\ln \sigma + \ln {A_1} - \frac{Q}{{RT}}, $ | (4) |
| $ \ln \dot \varepsilon = \beta \sigma + \ln {A_2} - \frac{Q}{{RT}}。$ | (5) |
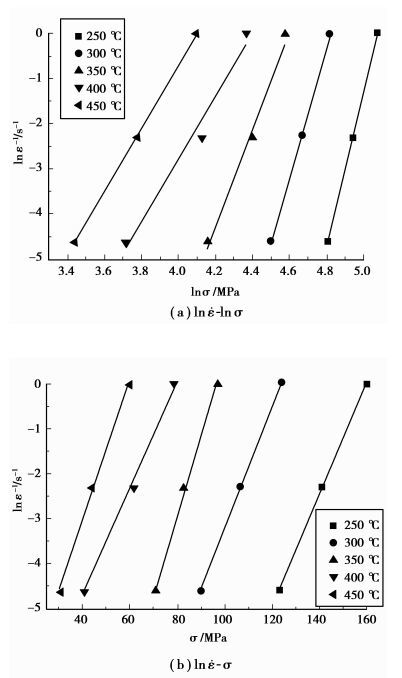
由式(4) 和式(5) 可知:在一定温度条件下,ln
|
图 3 AZ31-0.5Sr-1.5Y的流变应力与温度和应变速率关系 |
当应变速率为常数时,假定在很小的温度范围内变形激活能Q为常数,对双曲正弦函数关系式两边取对数有:
| $ \ln \dot \varepsilon = n\ln \left[ {\sin \mathit{h}\left( {\alpha \sigma } \right)} \right] + \ln A - \frac{Q}{{RT}}。$ | (6) |
对式(6) 两边求偏微分并整理有:
| $ Q = R\frac{{\partial \ln \dot \varepsilon }}{{\partial \ln \left[ {\sin \mathit{h}\left( {\alpha \sigma } \right)} \right]}}\left| {_T} \right.\frac{{\partial \ln \left[ {\sin \mathit{h}\left( {\alpha \sigma } \right)} \right]}}{{\partial \frac{1}{T}}}\left| {_{\dot \varepsilon }} \right. = Rnb, $ | (7) |
式中:
| $ n = \frac{{\partial \ln \dot \varepsilon }}{{\partial \ln \left[ {\sin \mathit{h}\left( {\alpha \sigma } \right)} \right]}}\left| {_T} \right., $ | (8) |
| $ b = \frac{{\partial \ln \left[ {\sin \mathit{h}\left( {\alpha \sigma } \right)} \right]}}{{\partial \frac{1}{T}}}\left| {_{\dot \varepsilon }} \right.。$ | (9) |
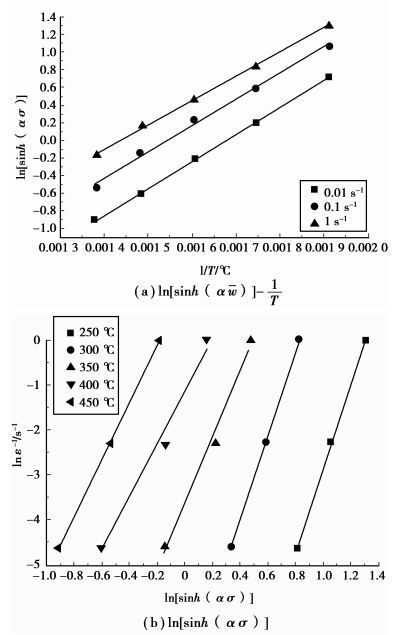
由式(8) 和式(9) 可知,n为图 4中ln
|
图 4 AZ31-0.5Sr-1.5Y的流变应力与温度和应变速率关系 |
| $ \dot \varepsilon = 3.295 \times {10^{14}}{\left[ {\sin \mathit{h}\left( {0.0127\sigma } \right)} \right]^{7.62}}\exp \left( { - \frac{{186.813}}{{RT}}} \right)。$ | (10) |
应变速率和变形温度之间的关系还可以用温度补偿的变形速率因子Zener-Hollomon参数来表示,其表达式为
| $ Z = \dot \varepsilon \exp \left( {\frac{Q}{{RT}}} \right)。$ | (11) |
将上述计算的各个参数代入式(11) 中,则可得含有温度补偿的速率因子Z参数的表达式为
| $ Z = \dot \varepsilon \exp \left( {\frac{{186.813}}{{RT}}} \right) = 3.295 \times {10^{14}}{\left[ {\sin \mathit{h}\left( {0.0127\sigma } \right)} \right]^{7.62}}。$ | (12) |
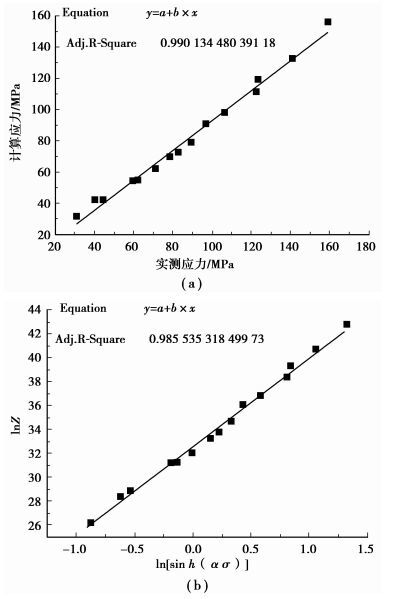
将变形温度和变形速率分别代入式(10) 和式(12) 中,可以分别得到图 5(a)计算应力与实际应力的比较图以及图 5(b)Z参数与流变应力之间的关系曲线图。由图 5可知,计算应力与实际应力较为吻合,其相关系数达到0.990 1以上;lnZ-ln[sinh(ασ)]也能够很好地满足直线关系,其相关系数达到0.985 5以上。说明双曲正弦函数能够很好地描述材料在热变形过程中的稳态流变应力。
|
图 5 计算应力与实测应力比较 |
加工图可以直观地反映出稳定变形区和失稳变形区,是加工变量空间中的功能耗散图与失稳图的叠加。功能耗散图是功能耗散速率因子随温度和应变速率变化的等值曲线图,反映了材料显微组织变化时所引起能量耗散[12-13]。其中功能耗散速率因子为
| $ \eta = \frac{{2m}}{{m + 1}}, $ | (13) |
式中:m为应变速率敏感指数,反映了材料在塑性变形过程中的瞬时能量分配关系,其值为
| $ m = \frac{{\partial \left( {\ln \sigma } \right)}}{{\partial \left( {\ln \dot \varepsilon } \right)}}。$ | (14) |
失稳图是根据不可逆热力学极值原理,用一个无量纲的参数表示最大塑性流变失稳判据。
| $ \xi \left( {\dot \varepsilon } \right) = \frac{{\partial \ln \left( {\frac{m}{{m + 1}}} \right)}}{{\partial \ln \dot \varepsilon }} + m < 0。$ | (15) |
当ξ(
|
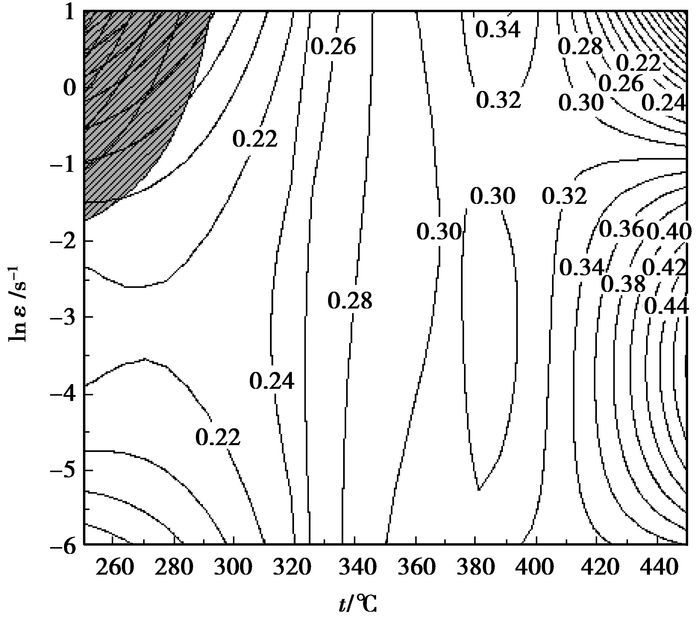
图 6 应变量为0.6时的AZ31-0.5Sr-1.5Y合金加工图 |
图 6中的阴影区为流变失稳区(ξ(
在加工图中除了上述流变失稳区外,还存在着功能耗散系数较大的区域,功能耗散系数反映了材料在变形过程中由组织转变所引起的能量耗散,因此功能耗散系数越大,在热变形过程中的组织转变也越大。当合金在350~400 ℃的温度区间内变形时,其功能耗散系数维持在30%左右。Avedesian[17]等人的研究表明:对于底层错能金属镁而言,当功能耗散系数大于30%时,便会发生动态再结晶:Slooff[18]等人在对AZ41、AZ61和AZ80的加工图进行研究时也得到了相似的结果。图 7(a)所示为合金在350 ℃,0.1 s-1条件下热压缩时的显微组织图。与原始铸态组织相比,AZ31-0.5Sr-1.5Y经热压缩后,原始铸态组织基本消失,被大量细小的再结晶晶粒所取代,说明合金在该区域发生了动态再结晶。当合金在400 ℃以上的较低应变速率区域变形时,其最大功能耗散系数最高可达46%,说明合金在这些区域变形时,其组织转变较大。通过对图 7(b)合金在450 ℃,0.01 s-1的显微组织进行观察可以发现,合金在该区域进行变形时,也发生了完全动态再结晶,但是其晶粒大小并不均匀,个别晶粒发生了异常长大。这与Ma[19]等人的观察结果一致。动态再结晶是受界面形成和界面迁移速率控制的过程,当界面迁移的速率大于界面形成的速率时,晶粒就会发生异常长大[20]。Anbuselvan[21]认为晶粒异常长大的出现会致使组织分布不均,从而致使变形不均,使得材料在加工过程中易于产生楔形裂纹。因此虽然合金该区域发生了完全动态再结晶,但它不是AZ31-0.5Sr-1.5Y合理的热加工区。其合理的热加工区为350~400 ℃和0.01~1 s-1。

|
图 7 AZ31-0.5Sr-1.5Y热压缩后的金相显微组织 |
1) AZ31-0.5Sr-1.5Y合金在热压缩过程中应力应变曲线呈现典型的动态再结晶特征,流变应力随应变速率的增加而增加,随温度的增加而减小;当变形速率一定时,随着温度的增加峰值应力所对应的应变左移,且峰值应力与稳态流变应力之间的差值减小。
2) 双曲正弦函数关系式能够很好地描述AZ31-0.5Sr-1.5Y合金材料变形过程中的流变应力,其函数表达式为:
3) 构建了AZ31-0.5Sr-1.5Y合金热加工图,当材料在低温(250~300 ℃),高应变速率(0.3~1 s-1)范围内成形时,会出现流变失稳;在高温(>400 ℃)时可能出现晶粒异常长大。在本实验条件下确定出的材料合理热加工工艺参数为:温度350~400 ℃,变形速率0.01~1 s-1。
| [1] |
肖盼, 刘天模, 姜丹.
AZ31镁合金的研究进展[J]. 重庆大学学报:自然科学版, 2006, 29(11): 81–84.
XIAO Pan, LIU Tianmo, JIANG Dan. Research status and development of AZ31 magnesium alloy[J]. Journal of Chongqing University:Science Edition, 2006, 29(11): 81–84. (in Chinese) |
| [2] | Wu L, Pan F S, Yang M B, et al. As-cast microstructure and Sr-containing phases of AZ31 magnesium alloys with high Sr contents[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(4): 784–789. DOI:10.1016/S1003-6326(11)60781-4 |
| [3] | Pan F S, Chen M B, Wang J F, et al. Effects of yttrium addition on microstructure and mechanical properties of as-extruded AZ31 magnesium alloys[J]. Transactions of Nonferrous Metals Society of China, 2008, 18(Sup): 81–86. |
| [4] | Chen G, Peng X D, Fan P G, et al. Effects of Sr and Y on microstructure and corrosion resistance of AZ31 magnesium alloy[J]. Transactions of Nonferrous Metal of China, 2011, 21(4): 725–731. DOI:10.1016/S1003-6326(11)60772-3 |
| [5] | Sadeghi A, Pekguleryuz M. Microstructure, mechanical properties and texture evolution of AZ31 alloy containing trace levels of strontium[J]. Materials characterization, 2011, 62(8): 742–750. DOI:10.1016/j.matchar.2011.05.006 |
| [6] | Tan C W, Xu S N, Chen Z Y, et al. Effect of temperature on mechanical behavior of AZ31 magnesium alloy[J]. Transactions of Nonferrous Metal of China, 2007, 17(1): 41–45. DOI:10.1016/S1003-6326(07)60045-4 |
| [7] |
黄光杰, 程虎.
3104铝合金流变应力行为[J]. 重庆大学学报:自然科学版, 2007, 30(1): 70–72.
HUANG Guangjie, CHENG Hu. Flow stress behavior of 3104 aluminum alloy[J]. Journal of Chongqing University:Science Edition, 2007, 30(1): 70–72. (in Chinese) |
| [8] | Huang X D, Zhang H, Han Y, et al. Hot deformation behavior of 2026 aluminum alloy during compression at elevated temperature[J]. Materials Science and Engineering A, 2010, 527(3): 485–490. DOI:10.1016/j.msea.2009.09.042 |
| [9] | Li H Z, Wang H J, Liang X P, et al. Hot deformation and processing map of 2519A aluminum alloy[J]. Materials Science and Engineering A, 2011, 528(3): 1548–1552. DOI:10.1016/j.msea.2010.10.080 |
| [10] |
范永革, 王凌云, 黄光胜, 等.
变形镁合金高温流变应力分析[J]. 重庆大学学报:自然科学版, 2003, 26(2): 9–11.
FAN Yongge, WANG Lingyun, HUANG Guangsheng, et al. Analysis of flow stress AZ31B wrought magnesium at elevated temperatures[J]. Journal of Chongqing University:Natural Science Edition, 2003, 26(2): 9–11. (in Chinese) |
| [11] | Zhang H, Jin N P, Chen J H. Hot deformation behavior of Al-Zn-Mg-Cu-Zr aluminum alloys during compression at elevated temperature[J]. Transactions of Nonferrous Metals Society of China, 2011, 21(3): 437–442. DOI:10.1016/S1003-6326(11)60733-4 |
| [12] |
曾卫东, 周义刚, 周军, 等.
加工图理论研究进展[J]. 稀有金属材料科学与工程, 2006, 35(5): 673–677.
ZENG Weidong, ZHOU Yigang, ZHOU Jun, et al. Recent development of processing map theory[J]. Rare Metal Materials and Engineering, 2006, 35(5): 673–677. (in Chinese) |
| [13] | Prasad Y V R K, Rao K P. Processing maps for hot deformation of rolled AZ31 magnesium alloy plate:Anisotropy of hot workability[J]. Materials Science and Engineering A, 2008, 487(1/2): 316–327. |
| [14] | Anbuselvan S, Ramanathan S. Hot deformation and processing maps of extruded ZE41 magnesium alloy[J]. Materials and Design, 2010, 31: 2319–2323. DOI:10.1016/j.matdes.2009.12.008 |
| [15] | Li D H, Yang Y, Xu T, et al. Observation of the microstructure in the adiabatic shear band of 7075 aluminum alloy[J]. Materials Science and Engineering A, 2010, 527(15): 3529–3535. DOI:10.1016/j.msea.2010.02.024 |
| [16] | Jain A, Agnew S R. Modeling the temperature dependent effect of twinning on the behavior of magnesium alloy AZ31B sheet[J]. Materials Science and Engineering A, 2007, 462(1/2): 29–36. |
| [17] | Avedesian M M, Baker H. ASM specialty hand-book-magnesium and magnesium alloys[M]. OH: ASM International, 1999. |
| [18] | Slooff F A, Dzwonczyk J S, ZHOU J, et al. Hot workability analysis of extruded AZ magnesium alloys with processing maps[J]. Materials Science and Engineering A, 2010, 527(3): 735–744. DOI:10.1016/j.msea.2009.08.070 |
| [19] | Ma M L, He L Q, Li X G, et al. Hot workability of Mg-9Y-1MM-0.6Zr alloy[J]. Journal of Rare Earths, 2011, 29(5): 460–465. DOI:10.1016/S1002-0721(10)60479-6 |
| [20] | Wang C W, Wang X J, Chang H, et al. Processing maps for hot working ZK60 magnesium alloy[J]. Materials Science and Engineering A, 2007, 464(1/2): 52–58. |
| [21] | Anbuselvan S, Ramanathan S, Karthikeyan R, et al. Development of processing maps for as-cast ZE41 magnesium alloy[J]. Nonferrous. Met, 2011, 21: 437–442. DOI:10.1016/S1003-6326(11)60733-4 |
 2013, Vol. 36
2013, Vol. 36

