众所周知,日益严峻的能源和环境问题是21世纪工业持续发展备受关注的问题[1-2]。轻合金在汽车工业中的应用可以显著减轻车重,降低油耗,并减小车辆的噪声、振动。而汽车油耗的75%与整车质量有关,质量每下降10%,油耗下降8%~10%,相应的排放下降4%;航空航天工业对减重的要求更是以克为单位。因此轻量化不仅能够解决能源和减少有害气体的排放,而且也是提高飞机、汽车等运载工具性能的重要途径[3]。铝合金和镁合金具有良好的性能,并可以回收再生利用,故镁铝合金材料是轻量化的首选金属材料[4-5]。
锰是铝合金和镁合金中常用的合金化元素,它能使合金的再结晶温度提高、晶粒细化[6-8];锰还可以提高合金的抗应力腐蚀的能力,降低其淬火敏感性,去除合金中的杂质铁等。目前ε-AlMn是镁合金晶粒细化研究的新热点,有可能成为镁合金的新型的晶粒细化剂[9-12],Al2Mn3是铝合金中常见的金属间化合物,它的存在可以提高铝合金的硬度和抗压强度[13]。另外,锰还能强化铁素体和细化珠光体,提高钢的淬透性、硬度和耐磨性等。在工业生产中,锰通常是以锰铝中间合金的形式加入。国内生产锰铝中间合金的主要工艺是对掺法、粉末冶金法、熔盐电解法和真空淬火法。其中对掺法是现阶段制取锰铝中间合金的主要生产工艺,但是锰属活泼金属,细粉状金属锰易被氧化,在空气中易燃烧,因此存在对掺过程中烧损严重等问题。自蔓延高温合成法(self-propagating high-temperature synthesis, SHS),也称燃烧合成法,是利用化学反应自身放热制备材料的新技术。它具有合成时间短,生产成本低,纯度高等优点。笔者以氧化锰和氧化钙为原料,金属铝为还原剂,探讨用自蔓延法来制取锰铝中间合金的一些基础问题,为拓展自蔓延高温合成技术和锰铝中间合金生产方法提供参考。
1 热力学计算 1.1 生成焓Miedema生成热模型是近年来合金化理论研究的一个重要模型,尝试利用合金组元的基本性质计算除O、S、Se、Te外的任何二元合金的生成热。在合金热力学性质的理论计算方面取得了良好的效果[14]。ΔHij的表达式如下:
| $ \begin{array}{*{20}{c}} {\Delta {H_{ij}} = F\left( {{x_i},V} \right)g\left( {{x_i},{n_{ws}}} \right)p\left[ {q/p{{\left( {\Delta n_{ws}^{\frac{1}{3}}} \right)}^2} - } \right.}\\ {\left. {p{{\left( {\Delta \varphi } \right)}^2} - \alpha \left( {\frac{r}{p}} \right)} \right],} \end{array} $ | (1) |
其中
| $ F\left( {{x_i},V} \right) = x_i^sx_j^s, $ | (2) |
| $ x_i^s = {x_i}V_{ia}^{\frac{2}{3}}/\left( {{x_i}V_{ia}^{\frac{2}{3}} + {x_j}V_{ja}^{\frac{2}{3}}} \right), $ | (3) |
| $ x_j^s = {x_j}V_{ja}^{\frac{2}{3}}/\left( {{x_i}V_{ia}^{\frac{2}{3}} + {x_j}V_{ja}^{\frac{2}{3}}} \right), $ | (4) |
| $ V_{ia}^{\frac{2}{3}} = V_i^{\frac{2}{3}}\left[ {1 + {\mu _i}{x_j}\left( {{\varphi _i} - {\varphi _j}} \right)} \right], $ | (5) |
| $ V_{ja}^{\frac{2}{3}} = V_j^{\frac{2}{3}}\left[ {1 + {\mu _j}{x_i}\left( {{\varphi _j} - {\varphi _i}} \right)} \right], $ | (6) |
| $ g\left( {{x_i},{n_{ws}}} \right) = \frac{{2{x_i}V_{ia}^{\frac{2}{3}} + 2{x_j}V_{ja}^{\frac{2}{3}}}}{{\left( {n_{ws}^{\frac{1}{3}}} \right)_i^{ - 1} + \left( {n_{ws}^{\frac{1}{3}}} \right)_j^{ - 1}}}, $ | (7) |
式中:φi为原子i的电负性;φj为原子j的电负性;(nws)i为i原子的电子密度参数;(nws)j为j原子的电子密度参数;Vi为i原子的摩尔体积;Vj为j原子的摩尔体积。
α、p、q、μ均为经验参数。Miedema[15]总结出经验参数取值规律,其中,q/p=9.4,液态合金α=0.73,固态合金α=1。碱金属元素μ=0.14;二价金属元素μ=0.10,三价金属元素和Cu,Ag,Au,μ=0.07;其他金属元素μ=0.04。对于p的取值,如果两种金属分别属于过渡元素和非过渡元素时p=12.3;如果都为过渡元素p=14.1;如果都为过渡元素和非过渡元素时p=10.6。至于r/p的取值,当两种合金元素都为非过渡元素或过渡元素时,r/p=0;如果分别属于过渡元素和非过渡元素时,r/p的值则与元素i和j在元素周期表中的具体位置有关。Al-Mn系的为1.9。Mn和Al的具体参数如表 1所示。通过公式(1) -(7) 可以算出Al2Mn3的标准生成焓为-41.39 kJ/mol。
| 表 1 Mn及Al的参数值 |
对于标准熵值的估算,Latimer[16]发明了一种方法估算主要离子化合物的标准熵,但对很多物质的计算误差很大,精度不高,属于半理论经验模型。赵定国[17]等建立了金属间化合物的双参数模型,用来估算金属间化合物的标准熵,且估算的标准差比离子束缚模型的要小,其绝对误差和相对误差均比离子束缚模型的要好,指标优于离子束缚模型,因此笔者运用双参数模型对Al2Mn3的熵值进行估算。对于金属间化合物MxNy,M和N为组成该化合物的金属符号,x和y分别为它们的系数,假定MxNy的比热容CP, 298g由两部分组成,一部分为单质金属的贡献熵,一部分为单质金属间的相互作用熵,其表达式如下:
| $ S_{P,298}^g = xA + yB + \frac{{xy}}{{x + y}}\left( {A' + B'} \right) + D, $ | (8) |
式中:CP, 298g为金属间化合物的比热容;A,A′为M的参数;B、B′为N的参数;D为常数。
由于每个金属间化合物均含有两个参数,因此将此模型称为标准熵的双参数模型,模型中的参数需要利用已知二元金属间化合物的标准熵求得。参数如表 2所示。Al2Mn3的标准熵为150.776 J/(K·mol)。
| 表 2 金属的A和A′值 |
比热容是金属化合物的重要的热力学性质,Kelley估算了许多在热化学文献中广泛应用的Cp-T关系方程,但是c值数据分散,涉及的参数也比较难确定[18],赵定国[19]等建立了估算二元金属间化合物比热容的双参数模型,来估算金属间化合物的比热容估算模型,误差较小,笔者采用双参数模型(式(8))对Al2Mn3的比热容进行估算。
模型中,取D=0.445 J/(K·mol)。模型中的参数需要利用已知二元金属间化合物的比热容通过回归方法求得,如表 3所示。Al2Mn3的比热容为121.412 4 J/(mol·K)。
| 表 3 金属的A和A′值(298 K) |
对自蔓延燃烧合成体系进行热力学理论分析,是研究合成反应能否自我维持、自我蔓延的基础。预测SHS过程实现可能性的最可信赖方法是计算给定混合体系的绝热燃烧温度。
绝热燃烧温度是反应的放热体系达到的最高温度,是描述SHS反应特征的主要热力学参数。Merzhangov[20]等人提出了以下经验判据,即当Tad≥1 800 K时,该SHS反应能自我维持,否则需要外界对体系补充能量。为了进行理论计算,假定体系绝热,反应在绝热温度条件下进行,且反应物100%的按化学计量比发生反应,放出的热量会全部用于反应方程中,如果反应在标准情况下进行,则有如下热平衡方程:
| $ \Delta H_{298}^\theta + \sum {{n_i}{{\left( {H_T^\theta - H_{298}^\theta } \right)}_{i,生成物}}} = 0, $ | (9) |
其中:ΔH298θ为物质在常温下(摩尔)的标准生成焓或反应在常温下的热效应。
绝热温度的计算可分为下面3种情况:
若Tad < Tm时
| $ - \Delta H_{298}^\theta = \int_{298}^{{T_{{\rm{ad}}}}} {\Delta {c_{p,产物}}{\rm{d}}T} ; $ | (10) |
若Tad=Tm时
| $ - \Delta H_{298}^\theta = \int_{298}^{{T_{\rm{m}}}} {\Delta {c_{p,产物}}{\rm{d}}T} + \nu \Delta {H_{\rm{m}}}。$ | (11) |
式中:ν为产物熔融状态的分数,取值范围为0 < ν < 1.0。
若Tad>Tm时
| $ \begin{array}{l} - \Delta H_{298}^\theta = \int_{298}^{{T_{\rm{m}}}} {\Delta {c_{p,产物}}{\rm{d}}T} + \Delta {H_{\rm{m}}} + \\ \int_{298}^{{T_{{\rm{ad}}}}} {\Delta {c_{p,产物}}{\rm{d}}T} > \int_{298}^{{T_{\rm{m}}}} {\Delta {c_{p,产物}}{\rm{d}}T} + \Delta {H_{\rm{m}}}。\end{array} $ | (12) |
对于反应
| $ {\rm{M}}{{\rm{n}}_2}{{\rm{O}}_3} + 3{\rm{M}}{{\rm{n}}_3}{{\rm{O}}_4} + 12{\rm{Al}} = 5{\rm{A}}{{\rm{l}}_2}{{\rm{O}}_3} + 8{\rm{Mn}} + {\rm{A}}{{\rm{l}}_2}{\rm{M}}{{\rm{n}}_3}, $ | (13) |
ΔH298θ=3 301 kJ/mol,解得Tad=3 160 K>1 800 K。
以上反应绝热温度的计算是在没有考虑熔化热的情况下计算得到的。体系若绝热,反应完全,Al2Mn3可被加热到熔化温度(1 348 K)以上。因此不再估算Al2Mn3的熔化热,其绝热温度都远高于1 800 K,由此说明该反应易于进行。
2 锰铝中间合金的合成 2.1 实验材料及方法实验材料为分析纯的二氧化锰,80~120目的纯Al粉。自蔓延法制取锰铝中间合金实验以Mn2O3和Mn3O4、CaO为原料,Al粉为还原剂。其中,Mn2O3和Mn3O4由MnO2分别加热到600 ℃、950 ℃得到[21]。
为了避免其他物料作为引燃剂而导致杂质的引入,采用Al粉和MnO2作为引燃剂,并用镁条点燃。从加料方式和Al粉粒度两方面来控制反应进行的速度,即逐步加料和选择80~120目合批的铝粉。同时,取铝粉过量150%,Mn2O3与Mn3O4质量比分别为3:1、3:2和1:3,CaO定量。
制取的锰铝中间合金进行化学成分分析、X射线衍射物相分析和金相显微组织分析等。
2.2 实验结果表 4是两种Mn2O3与Mn3O4配比下所制取中间合金的分析结果。从表 4可以看出,m(Mn2O3):m(Mn3O4)=3:2的情况下,锰的含量较高,而且收得率也最好。这与文献介绍两者活性氧在约8%时锰的回收率最高相吻合,因此对此种情况下制取得到的锰铝中间合金进行X射线衍射分析和金相观察。
| 表 4 Mn2O3与Mn3O4配比所制取中间合金的收得率 |
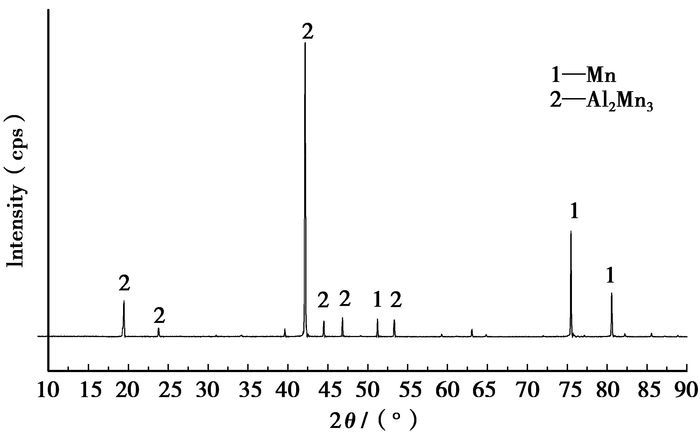
图 1是燃烧合成产物的X射线衍射分析结果。由图 1可知,合金产物的主要物相为Mn、Al2Mn3。
|
图 1 锰铝中间合金X射线衍射谱 |
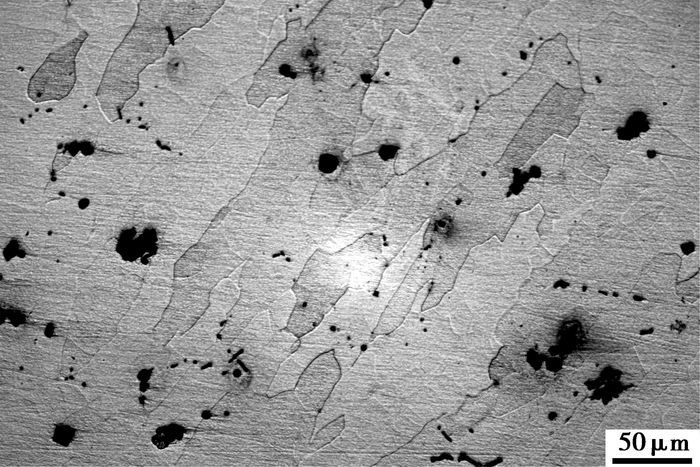
图 2为锰铝中间合金的金相照片。从图 2可以看出,有一相较凸出地分布在基体相上,这是由于生成物在反应后空冷,冷却速度缓慢,而且锰含量高,易形成铝锰金属间化合物,并以粗大块网状形式存在,才会出现一相凸出地分布在基体表面,通过图 1的金相分析以及中间合金的X射线衍射图谱,可以确定凸出相为铝锰金属间化合物,细小的豆粒状为单质锰的腐蚀坑,基体为Al2Mn3。
|
图 2 中间合金的金相照片 |
1) 通过对Al2Mn3的热力学数据进行了估算,其标准生成焓为-41.39 kJ/mol,标准熵为150.776 J/(K·mol),比热容为121.412 4 J/(mol·K)。
2) 实验体系的绝热温度为3 160 K以上,即利用自蔓延反应制取含Al2Mn3的锰铝中间合金在理论上是可行的。
3) 采用本自蔓延法合成方法,可以制取高锰含量的锰铝中间合金。
| [1] |
王晓强, 李培杰, 刘明星, 等.
镁合金再生技术综述[J]. 铸造, 2001, 50(8): 446–449.
WANG Xiaoqiang, LI Peijie, LIU Mingxing, et al. Review on recycling technique of magnesium alloy[J]. Foundry, 2001, 50(8): 446–449. (in Chinese) |
| [2] | 付东. 汽车轻量化材料及技术[G]//中国汽车工程学会. 2008中国汽车工程学会年会论文集. 北京: 机械工业出版社, 2008, 720-723. |
| [3] |
杨合, 李落星, 王渠东, 等.
轻合金成形领域科学技术发展研究[J]. 机械工程学报, 2010, 46(12): 31–41.
YANG He, LI Luoxing, WANG Qudong, et al. Research on the development of advanced forming for lightweight alloy materials area[J]. Journal of Mechanical Engineering, 2010, 46(12): 31–41. (in Chinese) |
| [4] |
郭瑞, 王兆文, 邱竹贤.
解析废铝再生的现状[J]. 有色矿冶, 2005, 21(3): 22–27.
GUO Rui, WANG Zhaowen, QIU Zhuxian. Simply analyzing the present situation of aluminum recycling[J]. Non-Ferrous Mining and Metallurgy, 2005, 21(3): 22–27. (in Chinese) |
| [5] |
丛福官.
镁合金的回收与再生[J]. 资源再生, 2007(5): 23–26.
CONG Fuguan. Reclaiming and recycle of magnesium alloy[J]. Resource Recycling, 2007(5): 23–26. (in Chinese) |
| [6] |
赵浩峰, 刘红梅, 张永忠, 等.
镁合金晶粒细化的研究[J]. 轻合金加工技术, 2004, 32(2): 10–13.
ZHAO Haofeng, LIU Hongmei, ZHANG Yongzhong, et al. Study about refining grain of magnesium alloy[J]. Light Alloy Fabrication Technology, 2004, 32(2): 10–13. (in Chinese) |
| [7] | 蒙多尔福. 铝合金的组织与性能[M]. 王祝堂, 张震录, 郑璇, 等, 译. 北京: 冶金工业出版社, 1988. |
| [8] |
林肇琦, 孙贵经, 胡维平, 等.
微量Mn对Al-Zn-Mg合金沉淀过程和显微组织参数的影响[J]. 金属学报, 1985, 21(2): 119–125.
LIN Zhaoqi, SUN Guijing, HU Weiping. Effect of Mn on precipitation and microstructural parameters of an Al-Zn-Mg alloy[J]. Acta Metallurgica Sinica, 1985, 21(2): 119–125. (in Chinese) |
| [9] |
刘子利, 沈以赴, 李子全, 等.
铸造镁合金的晶粒细化技术[J]. 材料科学与工程学报, 2004, 22(1): 146–149.
LIU Zili, SHEN Yifu, LI Ziquan, et al. Review of the grain refinement technology of cast magnesium alloys[J]. Journal of Materials Science and Engineering, 2004, 22(1): 146–149. (in Chinese) |
| [10] | Li S S, Zheng W C, Tang B, et al. Grain coarsening behavior of Mg-Al alloys with mischmetal addition[J]. Journal of Rare Earths, 2007, 25(2): 227–232. DOI:10.1016/S1002-0721(07)60078-7 |
| [11] | Motegi T, Yano E. Clarification of grain refining mechanisms of superheat-treated Mg-Al-Zn alloy castings[J]. Materials Science Forum, 2000(350/351): 191–198. |
| [12] | Tamura Y, Motegi T, Kono N, et al. Effect of minor elements on grain size of Mg-9%Al alloy[J]. Materials Science Forum, 2000(350/351): 199–204. |
| [13] | 史鹏飞. 高强度铝合金及高熵合金的组织结构与性能[D]. 长春: 吉林大学硕士学位论文, 2006. |
| [14] |
丁学勇, 范鹏, 韩其勇.
三元系金属熔体中的活度和活度相互作用系数模型[J]. 有色金属学报, 1994, 30(2): 49–60.
DING Xueyong, FAN Peng, HAN Qiyong. Models of activity and activity interaction parameter in ternary metallic melt[J]. Acta Metallurgica Sinica, 1994, 30(2): 49–60. (in Chinese) |
| [15] | Miedema A R, Chatel P F, Boer F R. Cohesion in alloys-fundamental of a semi-empirical model[J]. Physica B+C, 1980, 100(1): 1–28. |
| [16] | Latimer W M. Methods of estimating the entropies of solid compounds[J]. Journal of the American Chemical Society, 1951, 73(4): 1480–1482. DOI:10.1021/ja01148a021 |
| [17] |
赵定国, 郭培民, 赵沛.
金属间化合物的标准熵估算模型[J]. 北京科技大学学报, 2010, 32(1): 27–31.
ZHAO Dingguo, GUO Peimin, ZHAO Pei. Estimation model for standard entropy of intermetallics[J]. Journal of University of Science and Technology Beijing, 2010, 32(1): 27–31. (in Chinese) |
| [18] | Kubaschewski O, Alcock C B. 冶金热化学[M]. 邱竹贤, 梁英教, 李席孟, 等, 译. 北京: 冶金工业出版社, 1985. |
| [19] |
赵定国, 郭培民, 赵沛.
金属间化合物的比热容估算模型[J]. 北京科技大学学报, 2010, 32(5): 565–569.
ZHAO Dingguo, GUO Peimin, ZHAO Pei. Estimating model of specific heat of intermetallics[J]. Journal of University of Science and Technology Beijing, 2010, 32(5): 565–569. (in Chinese) |
| [20] | 殷声. 燃烧合成[M]. 北京: 冶金工业出版社, 2004. |
| [21] | 许传才. 铁合金冶炼工艺学[M]. 北京: 冶金工业出版社, 2008. |
 2013, Vol. 36
2013, Vol. 36

