冶金工程领域有许多过程涉及一维扩散。钢液精炼时，喷入钢液中粉粒内的传质^[1]；确定对流传质系数时，涉及的边界层层流底层内的扩散或相界面两侧膜内扩散^[1]；扩散系数的实验确定涉及的扩散实验^[2]等。这些例子涉及的扩散是分子扩散，扩散方程中的扩散系数D是分子扩散系数。几种扩散机理同时作用形成的物质浓度的变化仍可用扩散方程描述，但方程中扩散系数应换为有效扩散系数D_e。冶金中涉及一维有效扩散的例子有：气体和致密的铁块矿反应时，气体通过固相产物层的扩散^[1-2]；气体和多孔的铁矿球团反应时，气体通过球团内部多孔固体的扩散^{[1, 3-9]}。

上述举例中，扩散方程都是在有限长度区间[a，b]应用的，因为扩散发生在粉粒内、矿块中、球团内、层流底层中。铁矿团块内的传质、喷入钢液内每个粉粒内的传质等过程涉及的一维扩散方程都是在比装置更小的尺度上描述反应器内传质问题。从反应器尺度研究问题时，这些传质问题可以看作发生在装置内某位置。当对整个反应器内流动与混合、热和质量传输、化学反应等进行综合数值模拟研究的时候，一般要求装置内更小尺度上的传质速率、反应速率等最好有明确的数学分析式^[10-14]。若装置内各个更小尺度上的(或者说某位置上的)传质速率等也需像整个装置的传输问题处理一样，采用数值的方法迭代计算，这样势必增大问题的复杂性，降低处理问题的效率。因此，装置内更小尺度上的速率问题基本上应该沿有明确分析结果的方向来研究。

但菲克扩散方程在无限长度区间[0，∞]或[-∞，∞]里有分析解(误差函数解^{[1, 2, 15-16]}或高斯解^[2])，在[a，b]这样有限长度的区间里，它们都没有除了无穷级数^{[1, 2, 15-16]}解之外的分析解。无穷级数解利用起来不方便^[15]，一般结合线图使用且最终利用结果也是近似值；由于对质量守恒原理、扩散物理本质体现地不明显、不直接，导出误差解、高斯解和级数解等所用的分离变量等纯数学方法工程上很少应用。因此，直接基于物质守恒原理、菲克扩散定律等，利用一定的过程，获得工程上可利用的非稳态扩散方程的近似分析解，兼有理论意义和实践意义。它还可避免对误差函数解的依赖，即要获得物质由此位置经有限距离向彼位置扩散过程的解时，可以避免将彼位置处理在无穷远处。

适应一维扩散方程在工程研究和实践中应用的前述发展方向，笔者将基于稳态近似法获得定义在[0，l]上非稳态扩散方程的近似分析解，并将分析解和有足够精确度的数值解做了对比，获得了较满意的结果。

1 处理动力学问题的稳态近似法

笔者工作获得的近似解是基于稳态近似法。它是处理连串反应动力学问题的一种方法^[17]。对连串反应：A→R→C。为了推得A生成最终产物C的速率方程，假设中间产物R的浓度c_R=const(或$\frac{\text{d}{{c}_{R}}}{\text{d}t}=0$)。在多相反应中，对由外膜传质、内扩散、界面反应等环节组成的串联式的动力学方程，也可由稳定近似法导出。例如，金属氧化反应速率就是在假设氧化膜内氧化气体浓度不随时间变化的前提下得到的^[18]；铁矿石未反应核模型，就是在产物层还原物质浓度c=const的稳态假设下推出的^[1-2]。稳态假设就是在非稳态问题处理过程中，而附加的某个(些)量随时间不变的有限约束。既然是假设，就会使结果出现偏差，因此又要求它是有限的约束，不致结果偏差大。从稳态近似法应用的例子看出：稳态假设的对象应该是诸多串行环节中的一个或几个环节，这就为了保证是有限约束。

其实，运用稳态假设，除了可以进行c=const假设，还可以进行$\frac{\text{d}c}{\text{d}t}$=const(或$\frac{{{\text{d}}^{2}}c}{\text{d}{{t}^{2}}}$=0) 的假设。c=const假设是$\frac{\text{d}c}{\text{d}t}$=const假设的特例；换言之，c=const假设比$\frac{\text{d}c}{\text{d}t}$=const假设施加的约束强，应用$\frac{\text{d}c}{\text{d}t}$=const假设获得的结果，与应用c=const假设获得的结果相比，更接近真实情况。

看如何利用$\frac{\text{d}c}{\text{d}t}$=const的假设获得下面非稳态扩散问题的近似解。

$ \frac{{\partial c}}{{\partial t}} = D\frac{{{\partial ^2}c}}{{\partial {x^2}}}, $

初始条件   t=0:x∈[0, l]，c=0；

边界条件   $t>0:x=0,D\frac{\partial c}{\partial x}{{|}_{x=0}}=\beta (c{{|}_{x=0}}-{{c}^{0}});x=l,\frac{\partial c}{\partial x}{{|}_{x=l}}=0$。

左边界外部流体介质的浓度为已知的c⁰，流体介质与左边界之间的传质通量m=β(c|_x=0-c⁰)。

2 利用稳态近似法获得扩散方程近似解的过程

上述非稳态问题的解就是要获得(0，l)内任一位置x的浓度c_x随时间变化的关系，见图 1，位置x处的浓度c_x只是时间t的函数，它的变化率是$\frac{\text{d}{{c}_{x}}}{\text{d}t}$。运用稳态近似法求c_x的步骤如下：

2.1 划分网格(离散方程)

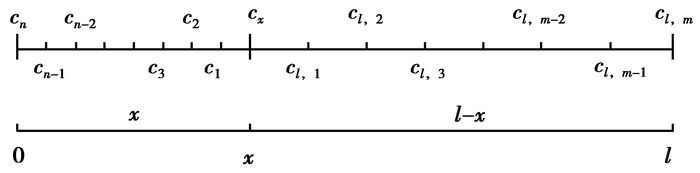
首先将位于x左边的区间长度x均分为n份，则每份的长度为$\frac{x}{n}$；位于x右边的区间长度l-x均分为m份，则每份的长度是$\frac{l-x}{m}$，如图 2所示。这样(0，l)内有(m-1) +(n-1) +1个间隔位置。将位于x左边第1个间隔位置处浓度记为c₁，位置x左边第2个间隔位置处浓度记为c₂，如图 2所示，以此类推，位于x左边第n-1间隔位置处浓度记为c_n-1，位于x左边第n间隔位置是区间[0，l]的左边界；按照同样做法，将位于x右边第1个间隔位置处浓度记为c_{l, 1}，位于x右边第2个间隔位置处浓度记为c_{l, 2}，以此类推，位于x右边第m-1间隔位置处浓度记为c_{l, m-1}，位于x右边第m个间隔位置是区间[0，l]的右边界。

与一般的数值方法一样^[19]，每个间隔位置处的浓度可以看作有自己的控制容积，间隔位置处的浓度可以用控制容积内的平均浓度代替，间隔位置处的浓度随时间的变化率可以用控制容积内的平均浓度随时间的变化率代替；若控制容积越小，间隔位置处的浓度和控制容积内的平均浓度越接近，间隔位置处浓度的变化率和控制容积内平均浓度的变化率越接近。浓度c₁，c₂，…，c_n-1的控制容积是$\frac{x}{n}$；浓度c_{l, 1}，c _{l, 2} …，c _{l, m-1}的控制容积是$\frac{l-x}{m}$；c_x的控制容积是$\frac{1}{2}\frac{x}{n}+\frac{1}{2}\frac{l-x}{m}$。这样可以将微分形式的扩散方程针对每个控制容积离散，例如对c_x的控制容积，扩散方程离散为

$ D\frac{{{c_1} - {c_x}}}{{\frac{x}{n}}} - D\frac{{{c_x} - {c_{l,1}}}}{{\frac{{l - x}}{m}}} = \frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)。$

(1)

注意，这里与一般数值方法不一样的是^[19]：浓度变化率(浓度对时间的导数)不离散，仅是关于对位置的导数的项离散；在c_x的控制容积内，$\frac{\partial c}{\partial t}$用$\frac{\text{d}{{c}_{x}}}{\text{d}t}$代替。对c₁，c₂，…，c_n-1的控制容积，扩散方程分别离散为

$ D\frac{{{c_2} - {c_1}}}{{\frac{x}{n}}} - D\frac{{{c_1} - {c_x}}}{{\frac{x}{n}}} = \frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}}\frac{x}{n}, $

(2-1)

$ D\frac{{{c_3} - {c_2}}}{{\frac{x}{n}}} - D\frac{{{c_2} - {c_1}}}{{\frac{x}{n}}} = \frac{{{\rm{d}}{c_2}}}{{{\rm{d}}t}}\frac{x}{n}, $

(2-2)

$ D\frac{{{c_4} - {c_3}}}{{\frac{x}{n}}} - D\frac{{{c_3} - {c_2}}}{{\frac{x}{n}}} = \frac{{{\rm{d}}{c_3}}}{{{\rm{d}}t}}\frac{x}{n}, $

(2-3)

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \cdots \\ D\frac{{{c_i} - {c_{i - 1}}}}{{\frac{x}{n}}} - D\frac{{{c_{i - 1}} - {c_{i - 2}}}}{{\frac{x}{n}}} = \frac{{{\rm{d}}{c_{i - 1}}}}{{{\rm{d}}t}}\frac{x}{n},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {2 - \left( {i - 1} \right)} \right] \end{array} $

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \cdots \\ D\frac{{{c_{n - 1}} - {c_{n - 2}}}}{{\frac{x}{n}}} - D\frac{{{c_{n - 2}} - {c_{n - 3}}}}{{\frac{x}{n}}} = \frac{{{\rm{d}}{c_{n - 2}}}}{{{\rm{d}}t}}\frac{x}{n},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {2 - \left( {n - 2} \right)} \right] \end{array} $

$ \begin{array}{l} D\frac{{{c_n} - {c_{n - 1}}}}{{\frac{x}{n}}} - D\frac{{{c_{n - 1}} - {c_{n - 2}}}}{{\frac{x}{n}}} = \frac{{{\rm{d}}{c_{n - 1}}}}{{{\rm{d}}t}}\frac{x}{n}。\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {2 - \left( {n - 1} \right)} \right] \end{array} $

左边界的边界条件$\frac{\partial c}{\partial x}{{|}_{x=0}}=\beta \left( c{{|}_{x=0}}-{{c}^{0}} \right)$离散为

$ \beta \left( {{c^0} - {c_n}} \right) - D\frac{{{c_n} - {c_{n - 1}}}}{{\frac{x}{n}}} = 0。$

(2-n)

对c_{l, 1}，c _{l, 2} …，c _{l, m-2}的控制容积，扩散方程分别离散为

$ D\frac{{{c_x} - {c_{l,1}}}}{{\frac{{l - x}}{m}}} - D\frac{{{c_{l,1}} - {c_{l,2}}}}{{\frac{{l - x}}{m}}} = \frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}}\frac{{l - x}}{m}, $

(3-1)

$ D\frac{{{c_{l,1}} - {c_{l,2}}}}{{\frac{{l - x}}{m}}} - D\frac{{{c_{l,2}} - {c_{l,3}}}}{{\frac{{l - x}}{m}}} = \frac{{{\rm{d}}{c_{l,2}}}}{{{\rm{d}}t}}\frac{{l - x}}{m}, $

(3-2)

$ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \cdots \\ D\frac{{{c_{l,m - 3}} - {c_{l,m - 2}}}}{{\frac{{l - x}}{m}}} - D\frac{{{c_{l,m - 2}} - {c_{l,m - 1}}}}{{\frac{{l - x}}{m}}} = \frac{{d{c_{l,m - 2}}}}{{{\rm{d}}t}}\frac{{l - 2}}{m}。\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {3 - \left( {m - 2} \right)} \right] \end{array} $

x=l处的边界条件$\frac{\partial c}{\partial x}$=0离散为

$ \frac{{{c_{l,m}} - {c_{l,m - 1}}}}{{\frac{{l - x}}{m}}} = 0。$

扩散方程在c_{l, m-1}的控制容积离散为

$ D\frac{{{c_{l,m - 2}} - {c_{l,m - 1}}}}{{\frac{{l - x}}{m}}} - D\frac{{{c_{l,m - 1}} - {c_{l,m}}}}{{\frac{{l - x}}{m}}} = \frac{{{\rm{d}}{c_{l,m - 1}}}}{{{\rm{d}}t}}\frac{{l - x}}{m}, $

结合右边界条件离散式，此式化为

$ \begin{array}{l} D\frac{{{c_{l,m - 2}} - {c_{l,m - 1}}}}{{\frac{{l - x}}{m}}} = \frac{{{\rm{d}}{c_{l,m - 1}}}}{{{\rm{d}}t}}\frac{{l - x}}{m}。\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {3 - \left( {m - 1} \right)} \right] \end{array} $

2.2 进行稳态假设

因要获得随时间变化的浓度c_x所在的位置x位于(0，l)内，即0＜x＜l。x左边浓度c₁的位置为：$x-\frac{x}{n}=\left( 1-\frac{1}{n} \right)x=\frac{n-1}{n}x>0\left( n\ge 2 \right)$。x右边浓度c_{l, 1}的位置为：$x+\frac{l-x}{m}＜x+l-x=l\left( m\ge 2 \right)$。因此只要m≥2、n≥2，浓度c₁和c_{l, 1}所在的位置也都位于(0，l)内。这样位置相邻的c₁、c_x、c_{l, 1}作为一个环节串联在整体之中，对它们可以进行稳态假设，运用稳态近似法了。假设：

$\frac{\text{d}{{c}_{1}}}{\text{d}t}=\text{cons}t$，即$\frac{{{\text{d}}^{2}}{{c}_{1}}}{\text{d}{{t}^{2}}}=0$；$\frac{\text{d}{{c}_{x}}}{\text{d}t}=\text{cons}t$，即$\frac{{{\text{d}}^{2}}{{c}_{x}}}{\text{d}{{t}^{2}}}=0;\frac{\text{d}{{c}_{l,\text{ }1}}}{\text{d}t}=\text{cons}t$，即$\frac{{{\text{d}}^{2}}{{c}_{l,\text{ }1}}}{\text{d}{{t}^{2}}}=0$。

2.3 导出c₁、c_x、c_{l, 1}满足的关系式

由式(1) 变形得：

$ \begin{array}{*{20}{c}} {{c_1} = \frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {c_x} + }\\ {\frac{m}{n}\frac{x}{{l - x}}{c_x} - \frac{m}{n}\frac{x}{{l - x}}{c_{l,1}},} \end{array} $

(2)

将c₁对时间求导，并结合假设得：

$ \frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + \frac{m}{n}\frac{x}{{l - x}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - \frac{m}{n}\frac{x}{{l - x}}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}}, $

(3)

由式(2-1) 变形得：

$ {c_2} = \frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}}{\left( {\frac{x}{n}} \right)^2}\frac{1}{D} + 2{c_1} - {c_x}。$

将$\frac{\text{d}{{c}_{1}}}{\text{d}t}$、c₁的表达式代入c₂，整理得：

$ \begin{array}{*{20}{c}} {{c_2} = {{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + \frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {2\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + 2\frac{m}{n}\frac{x}{{l - x}}{c_x} - 2\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}}。} \end{array} $

将c₂对时间求导，得：

$ \frac{{{\rm{d}}{c_2}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + 2\frac{m}{n}\frac{x}{{l - x}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - 2\frac{m}{n}\frac{x}{{l - x}}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}}。$

由式(2-2) 变形得：

$ {c_3} = \frac{{{\rm{d}}{c_2}}}{{{\rm{d}}t}}{\left( {\frac{x}{n}} \right)^2}\frac{1}{D} + 2{c_2} - {c_1}。$

将$\frac{\text{d}{{c}_{2}}}{\text{d}t}$、c₂和c₁的表达式代入c₃，整理得：

$ \begin{array}{*{20}{c}} {{c_3} = 3{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + 4\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {4\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {3\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + 3\frac{m}{n}\frac{x}{{l - x}}{c_x} - 3\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}}。} \end{array} $

综合c₂和c₃表达式的形式，令：

$ \begin{array}{*{20}{c}} {{c_i} = {A_i}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {B_i}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_i}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {{C_i}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + {C_i}\frac{m}{n}\frac{x}{{l - x}}{c_x} - {C_i}\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}}。} \end{array} $

(4)

则：

$ \begin{array}{*{20}{c}} {{c_{i - 1}} = {A_{i - 1}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {B_{i - 1}}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_{i - 1}}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {{C_{i - 1}}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + {C_{i - 1}}\frac{m}{n}\frac{x}{{l - x}}{c_x} - {C_{i - 1}}\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}},} \end{array} $

$ \begin{array}{*{20}{c}} {{c_{i - 2}} = {A_{i - 2}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{B_{i - 2}}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_{i - 2}}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {{C_{i - 2}}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + {C_{i - 2}}\frac{m}{n}\frac{x}{{l - x}}{c_x} - {C_{i - 2}}\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}}。} \end{array} $

将c_i-1对时间求导，并结合假设得：

$ \frac{{{\rm{d}}{c_{i - 1}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {C_{i - 1}}\frac{m}{n}\frac{x}{{l - x}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - {C_{i - 1}}\frac{m}{n}\frac{x}{{l - x}}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}}。$

由式[2-(i-1)]变形得：

$ {c_i} = \frac{{{\rm{d}}{c_{i - 1}}}}{{{\rm{d}}t}}{\left( {\frac{x}{n}} \right)^2}\frac{1}{D} + 2{c_{i - 1}} - {c_{i - 2}}, $

将$\frac{\text{d}{{c}_{i-1}}}{\text{d}t}$、c_i-1和c_i-2的表达式代入c_i，合并同类项后得：

$ \begin{array}{*{20}{c}} {{c_i} = \left( {2{A_{i - 1}} - {A_{i - 2}} + 1} \right){{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + \left( {2{B_{i - 1}} - } \right.}\\ {\left. {{B_{i - 2}} + {C_{i - 1}}} \right)\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\left( {2{B_{i - 1}} - {B_{i - 2}} + {C_{i - 1}}} \right)\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {\left( {2{C_{i - 1}} - {C_{i - 2}}} \right)\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + \left( {2{C_{i - 1}} - {C_{i - 2}}} \right)\frac{m}{n}\frac{x}{{l - x}}{c_x} - }\\ {\left( {2{C_{i - 1}} - {C_{i - 2}}} \right)\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}}。} \end{array} $

将此式和式(4) 比照，得A_i、B_i和C_i的递推公式(i≥4)：

$ {A_i} = 2{A_{i - 1}} - {A_{i - 2}} + 1,{A_2} = 1,{A_3} = 3; $

$ {B_i} = 2{B_{i - 1}} - {B_{i - 2}} + {C_{i - 1}},{B_2} = 1,{B_3} = 4; $

$ {C_i} = 2{C_{i - 1}} - {C_{i - 2}},{C_2} = 2,{C_3} = 3。$

A₂、A₃、B₂、B₃、C₂、C₃是c₂、c₃表达式中相应项前面的系数。由A_i、B_i和C_i的递推公式及相应前两项的值可推得：${{A}_{i}}=\frac{\left( i-1 \right)\text{ }i}{2};{{B}_{i}}=\frac{\left( i-1 \right)\text{ }i\left( i+1 \right)}{6}\text{ };{{C}_{i}}=i$。

由式[2-(n-2)](这时i=n-1) 得：

$ \begin{array}{*{20}{c}} {{c_{n - 1}} = {A_{n - 1}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {B_{n - 1}}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_{n - 1}}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {{C_{n - 1}}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + {C_{n - 1}}\frac{m}{n}\frac{x}{{l - x}}{c_x} - {C_{n - 1}}\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}}。} \end{array} $

由式[2-(n-1)](这时i=n)得：

$ \begin{array}{*{20}{c}} {{c_n} = {A_n}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {B_n}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_n}\frac{m}{n}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} + }\\ {{C_n}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{x}{n}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + {C_n}\frac{m}{n}\frac{x}{{l - x}}{c_x} - {C_n}\frac{m}{n}\frac{x}{{l - x}}{c_{l,1}},} \end{array} $

将c_n和c_n-1代入式(2-n)，整理得到c_x、c_{l, 1}满足的一个关系式：

$ \begin{array}{*{20}{c}} {\frac{1}{D}\frac{x}{n}\beta {c^0} - \beta \frac{{n\left( {n - 1} \right)}}{2}{{\left( {\frac{x}{n}} \right)}^3}\frac{1}{{{D^2}}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\beta \frac{{\left( {n - 1} \right)\left( {n + 1} \right)m}}{6}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^3}\frac{1}{{{D^2}}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {\beta \frac{{\left( {n - 1} \right)\left( {n + 1} \right)m}}{6}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^3}\frac{1}{{{D^2}}}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} - }\\ {\beta n\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right){{\left( {\frac{x}{n}} \right)}^2}\frac{1}{{{D^2}}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{1}{D}\frac{x}{n}\beta {c_x} - \frac{m}{D}\frac{x}{n}\beta \frac{x}{{l - x}}{c_x} + \frac{m}{D}\frac{x}{n}\beta \frac{x}{{l - x}}{c_{l,1}} - }\\ {\frac{1}{D}\left( {n - 1} \right){{\left( {\frac{x}{n}} \right)}^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - \frac{1}{D}\frac{{\left( {n - 1} \right)m}}{2}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {\frac{1}{D}\frac{{\left( {n - 1} \right)m}}{2}\frac{x}{{l - x}}{{\left( {\frac{x}{n}} \right)}^2}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} - }\\ {\frac{1}{D}\frac{x}{n}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{m}{n}\frac{x}{{l - x}}{c_x} + \frac{m}{n}\frac{x}{{l - x}}{c_{l,1}} = 0。} \end{array} $

(5)

按照同样的做法，可以推得浓度c_{l, i}的通式：

$ \begin{array}{*{20}{c}} {{C_{l,i}} = {A_i}\left( {\frac{{l - x}}{m}} \right)^2\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {B_i}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_i}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}} + }\\ {{C_i}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{{l - x}}{m}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_x} + {C_i}\frac{n}{m}\frac{{l - x}}{x}{c_x} - {C_i}\frac{n}{m}\frac{{l - x}}{x}{c_1}。} \end{array} $

其中A_i、B_i和C_i的计算式分别为：${{A}_{i}}=\frac{\left( i-1 \right)\text{ }i}{2};{{B}_{i}}=\frac{\left( i-1 \right)\text{ }i\left( i+1 \right)}{6};{{C}_{i}}=i(4\le i\le m-1)$。

令i=m-2得：

$ \begin{array}{*{20}{c}} {{c_{l,m - 2}} = {A_{m - 2}}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{B_{m - 2}}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_{m - 2}}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}} + }\\ {{C_{m - 2}}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{{l - x}}{m}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_s} + {C_{m - 2}}\frac{n}{m}\frac{{l - x}}{x}{c_x} - {C_{m - 2}}\frac{n}{m}\frac{{l - x}}{x}{c_1}。} \end{array} $

令i=m-1得：

$ \begin{array}{*{20}{c}} {{c_{l,m - 1}} = {A_{m - 1}}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{B_{m - 1}}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{B_{m - 1}}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}} + }\\ {{C_{m - 1}}\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{{l - x}}{m}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {{c_s} + {C_{m - 1}}\frac{n}{m}\frac{{l - x}}{x}{c_x} - {C_{m - 1}}\frac{n}{m}\frac{{l - x}}{x}{c_1}。} \end{array} $

将上式对时间t求导，得：

$ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}{c_{l,m - 1}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + {C_{m - 1}}\frac{n}{m}\frac{{l - x}}{x}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {{C_{m - 1}}\frac{n}{m}\frac{{l - x}}{x}\frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}}。} \end{array} $

将$\frac{\text{d}{{c}_{l,~m-1}}}{\text{d}t}$、c_{l, m-1}和c_{l, m-2}的表达式代入式[3-(m-1)]，整理得c_x、c1满足的一个关系式：

$ \begin{array}{*{20}{c}} {\left( {m - 1} \right){{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {\frac{{m\left( {m - 1} \right)}}{2}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{{m\left( {m - 1} \right)}}{2}\frac{n}{m}\frac{{l - x}}{x}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_1}}}{{{\rm{d}}t}} + }\\ {\frac{1}{D}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{{l - x}}{m}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {\frac{n}{m}\frac{{l - x}}{x}{c_x} - \frac{n}{m}\frac{{l - x}}{x}{c_1} = 0。} \end{array} $

(6)

2.4 导出c_x关于t的函数关系式

将c₁、$\frac{\text{d}{{c}_{1}}}{\text{d}t}$的表达式[式(2) 和式(3)]代入式(6)，整理之后得到下式：

$ \begin{array}{*{20}{c}} {\left( {m - 1} \right){{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{{m\left( {m - 1} \right)}}{2}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + }\\ {\frac{{m\left( {m - 1} \right)}}{2}{{\left( {\frac{{l - x}}{m}} \right)}^2}\frac{1}{D}\frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} - {c_x} + {c_{l,1}} = 0。} \end{array} $

(7)

将式(9) 两边同时对时间求导，并结合假设得：

$ \frac{{{\rm{d}}{c_{l,1}}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}。$

将$\frac{\text{d}{{c}_{l,\text{ }1}}}{\text{d}t}=\frac{\text{d}{{c}_{x}}}{\text{d}t}$代入式(5) 得：

$ \begin{array}{*{20}{c}} {\frac{1}{D}\frac{x}{n}\beta {c^0} - \beta \frac{{n\left( {n - 1} \right)}}{2}{{\left( {\frac{x}{n}} \right)}^3}\frac{1}{{{D^2}}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\beta n\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right){{\left( {\frac{x}{n}} \right)}^2}\frac{1}{{{D^2}}}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}}\\ { - \frac{1}{D}\frac{x}{n}\beta {c_x} - \frac{m}{D}\frac{x}{n}\beta \frac{x}{{l - x}}{c_x} + \frac{m}{D}\frac{x}{n}\beta \frac{x}{{l - x}}{c_{l,1}} + }\\ {\frac{1}{D}\left( {1 - n} \right){{\left( {\frac{x}{n}} \right)}^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{1}{D}\frac{x}{n}\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{m}{n}\frac{x}{{l - x}}{c_x} + \frac{m}{n}\frac{x}{{l - x}}{c_{l,1}} = 0。} \end{array} $

(8)

将$\frac{\text{d}{{c}_{l,\text{ }1}}}{\text{d}t}=\frac{\text{d}{{c}_{x}}}{\text{d}t}$代入式(7) 得：

$ \left( {m - 1} \right){\left( {\frac{{l - x}}{m}} \right)^2}\frac{1}{D}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - {c_x} + {c_{l,1}} = 0。$

(9)

将式(8) ×n(l-x)-式(9) ×$\left( mx+m\frac{\beta }{D}{{x}^{2}} \right)$，并整理之后得：

$ \begin{array}{*{20}{c}} {\frac{1}{D}\beta x\left( {l - x} \right){c^0} - \frac{{n - 1}}{n}\frac{1}{{2{D^2}}}\beta {x^3}\left( {l - x} \right)\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{1}{{{D^2}}}\beta \left( {l - x} \right){x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{{m - 1}}{m}\frac{1}{{{D^2}}}\beta {{\left( {l - x} \right)}^2}{x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + \frac{{1 - n}}{n}\frac{1}{D}\left( {l - x} \right){x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right)\frac{1}{D}x\left( {l - x} \right)\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{{m - 1}}{m}\frac{1}{D}x{{\left( {l - x} \right)}^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - \frac{1}{D}\beta x\left( {l - x} \right){c_x} = 0。} \end{array} $

(10)

要让n、m趋无穷大，每一个控制容积才会趋近于0，每个间隔位置处的浓度和控制容积内的平均浓度才相等，每个间隔位置处的浓度变化率和控制容积内的平均浓度变化率才相等。对式(10) 两边同时取极限：

$ \begin{array}{*{20}{c}} {\frac{1}{D}\beta x\left( {l - x} \right){c^0} - \frac{1}{{2{D^2}}}\beta {x^3}\left( {l - x} \right)\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}\mathop {\lim }\limits_{n \to \infty } \frac{{n - 1}}{n} - }\\ {\frac{1}{{{D^2}}}\beta \left( {l - x} \right){x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}\mathop {\lim }\limits_{\begin{array}{*{20}{c}} {n \to \infty }\\ {m \to \infty } \end{array}} \left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right) - }\\ {\frac{1}{{{D^2}}}\beta {{\left( {l - x} \right)}^2}{x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}\mathop {\lim }\limits_{m \to \infty } \frac{{m - 1}}{m} + }\\ {\frac{1}{D}\left( {l - x} \right){x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}\mathop {\lim }\limits_{n \to \infty } \frac{{1 - n}}{n} - }\\ {\frac{1}{D}x\left( {l - x} \right)\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}\mathop {\lim }\limits_{\begin{array}{*{20}{c}} {n \to \infty }\\ {m \to \infty } \end{array}} \left( {\frac{1}{2}\frac{x}{n} + \frac{1}{2}\frac{{l - x}}{m}} \right) - }\\ {\frac{1}{D}x{{\left( {l - x} \right)}^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}}\mathop {\lim }\limits_{m \to \infty } \frac{{m - 1}}{m} - \frac{1}{D}\beta x\left( {l - x} \right){c_x} = 0。} \end{array} $

即：

$ \begin{array}{*{20}{c}} {\frac{1}{D}\beta x\left( {l - x} \right){c^0} - \frac{1}{{2{D^2}}}\beta {x^3}\left( {l - x} \right)\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{1}{{{D^2}}}\beta {{\left( {l - x} \right)}^2}{x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{1}{D}\left( {l - x} \right){x^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - \frac{1}{D}x{{\left( {l - x} \right)}^2}\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} - }\\ {\frac{1}{D}\beta x\left( {l - x} \right){c_x} = 0。} \end{array} $

上式两边同时除以$\frac{l}{D}x\left( l-x \right)$后，经整理得到：

$ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}{c_x}}}{{{\rm{d}}t}} + \frac{\beta }{{\frac{1}{{2D}}\beta {x^2} + \frac{1}{D}\beta x\left( {l - x} \right) + l}}{c_x} = }\\ {\frac{\beta }{{\frac{1}{{2D}}\beta {x^2} + \frac{1}{D}\beta x\left( {l - x} \right) + l}}{c^0}。} \end{array} $

(11)

式(11) 是关于时间t的一阶线性微分方程，它的通解为

$ {c_x} = C{\rm{e}}\frac{{ - \beta }}{{\frac{1}{{2D}}\beta {x^2} + \frac{1}{D}\beta x\left( {l - x} \right) + l}}t + {c^0}。$

加入初始条件(t=0时，c_x=0) 限制，确定积分常数C后，最终得：

$ {c_x} = - {c^0}{\rm{e}}\frac{{ - \beta }}{{\frac{1}{{2D}}\beta {x^2} + \frac{1}{D}\beta x\left( {l - x} \right) + l}}t + {c^0}。$

(12)

式(14) 可看作前述非稳态扩散问题的一个近似解。

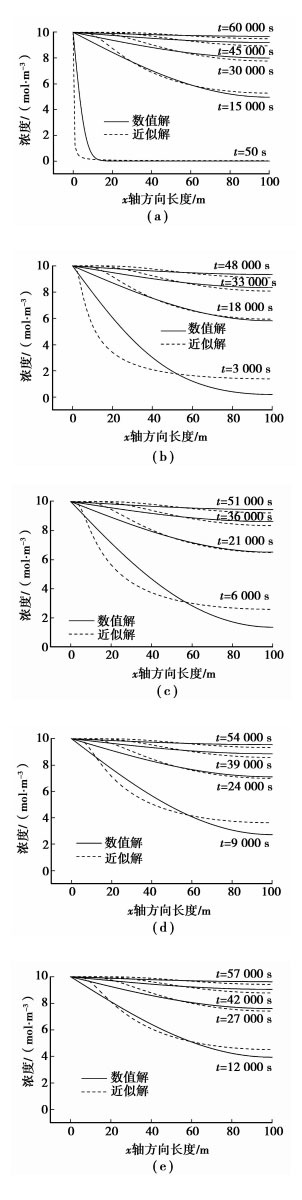
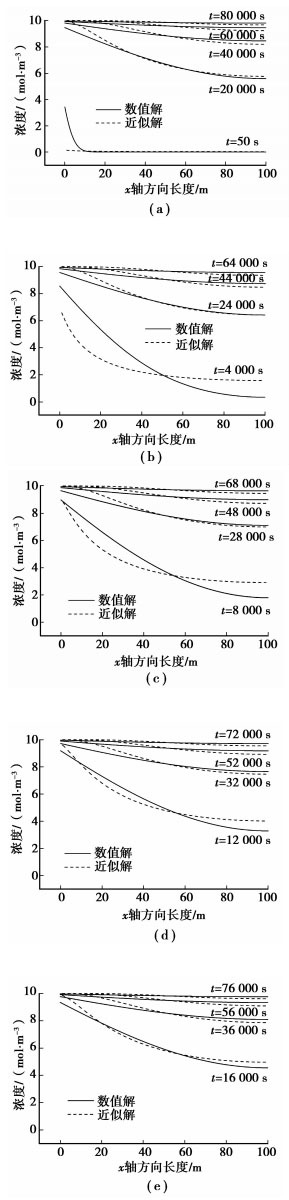
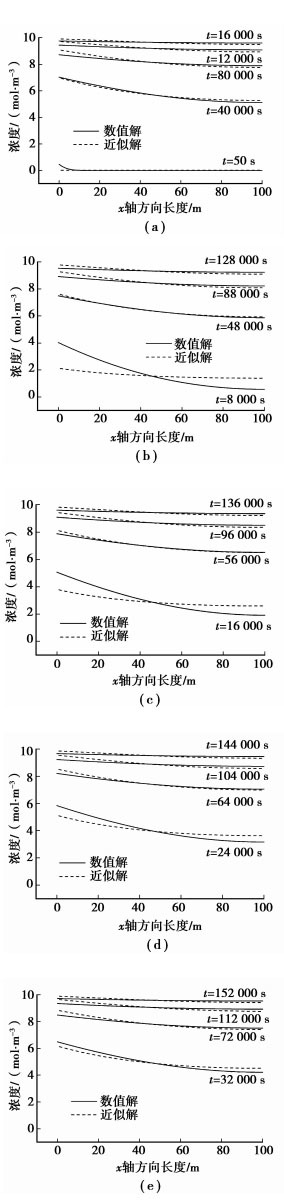
3 所求近似解和数值解的对比

对前述非稳态扩散问题，取c⁰=10 mol/m³，l=100 m，D=0.25 m²/s，β分别取300，0.03，0.003 m/s；按照通常的数值方法^[19]获得它的数值解，计算数值解时，均匀网格数取1 000 (即Δx=0.1 m)，时间步长(Δt)取1s。网格再加密，时间步长再缩短，均看不出数值解再有变化，这时的数值解其实就可看作是此例非稳态问题的精确解。此例非稳态问题的数值解用图 3、图 4、图 5中的实线示出。按式(12) 中c_x的近似解表达式计算的结果用这些图中的虚线示出。图 3(a)、(b)、(c)、(d)、(e)各图，在传质系数β取300 m/s时，对扩散开始后的50，3 000，6 000，9 000，…，一直到接近最终稳态的54 000，57 000，60 000s等时刻点的近似解和数值解进行了对比。同样地，图 4和图 5，在传质系数β分别取0.03 m/s和0.003 m/s时，对扩散开始后，一直到接近最终稳态的一些时刻点的近似解和数值解进行了对比。图 3、图 4、图 5较全面地反映了式(12) 中c_x的近似解与精确解的吻合情况。

从近似解和数值解对比可以看出：两者吻合程度总体是较好的；在扩散的前期(图 3中0~9 000 s，图 4中0~12 000 s，图 5中0~24 000 s)，两者曲线形状吻合稍差些，但前期过后，一直到最终稳态，两者曲线形状吻合比较好。另外：从扩散开始到最终达到稳态的漫长时间里(图 3、图 4、图 5是算例条件下的结果，如选实际物质固态金属中的扩散来计算，扩散时间更是漫长的)，近似解和数值解是同步的，因此用此近似解预测达到最终稳态的时间，准确度应该是好的；从近似解和数值解对比来看，两者没有出现错位，在内部扩散占控制地位$\left( \frac{1}{\beta }\ll \frac{l}{D} \right)$的图 3中，两者总有2~3个交点，在外部传质占控制地位$\left( \frac{1}{\beta }\gg \frac{l}{D} \right)$的图 5中，在同一时刻的近似解和数值解基本上都呈直线，但两者总有交点，即使经过漫长的扩散发展过程，同一时刻的近似解和数值解也不会出现一条曲线完全在上另一条曲线完全在下的错位。总体来说：近似解是可以接受的。扩散方程分析解的稳态近似法可以说是有效的。

若在获得前述非稳态问题近似解的过程中，稳态假设改为c₁=const，即$\frac{\text{d}{{c}_{1}}}{\text{d}t}$=0；c_x=const，即$\frac{\text{d}{{c}_{x}}}{\text{d}t}$=0；c_{l, 1}=const，即$\frac{\text{d}{{c}_{l,\text{ }1}}}{\text{d}t}$=0，按照前述的方法和步骤，最终可得到的近似解为：c_x=c⁰。这个近似解说明在各时刻c_x的近似值都是最终稳态的值。这个近似解和实际情形差别较大。但工程上得到应用的未反应核模型、金属氧化模型等都是在假设产物层还原或氧化气体浓度c=const($\frac{\text{d}c}{\text{d}t}$=0) 得到的，c_x的结果会有它的启示和比较的作用，也称其为近似解。浓度不随时间变化稳态假设下的近似解就是最终稳态的解，意味着稳态近似法处理的结果可能首先从近似最终稳态开始，然后可能接着近似接近最终稳态的状态，再接着可能近似远离最终稳态的状态。这种理解与图 3、图 4、图 5中出现的近似解和数值解吻合现象比较符合。

另外，从图 3、图 4、图 5中还可以看出，近似解基本上是遵循总体质量守恒的，也即同一时刻近似解曲线和数值解曲线下面的面积是基本相同的。可明显看出(尤其从图 5)近似解曲线位于数值解曲线上面的面积和它位于数值解曲线下面的面积基本是相同的。但在扩散前期，比如看图 3，近似解曲线位于数值解曲线上面的面积和它位于数值解曲线下面的面积在50，3 000，6 000 s时刻是有稍大些的差别。近似解基本上是遵循总体质量守恒的，这也可由近似解和数值解是同步的结论意识到；而在扩散前期，近似解满足总体质量守恒程度稍差是由稳态近似法的特点决定的，稳态近似法处理的结果首先从近似最终稳态开始。

4 结论

1) 首先将动力学中常用的浓度随时间不变的稳态假设发展为浓度变化率随时间不变的稳态假设。给出了对在有限长度区间内应用的扩散方程进行稳态近似法处理的过程。

2) 对文中给出的非稳态问题获得的近似解为：${{c}_{x}}=-{{c}^{0}}{{\text{e}}^{\frac{-\beta }{\frac{1}{2D}\beta {{x}^{2}}+\frac{1}{D}\beta x\left( l-x \right)+l}t}}+{{c}^{0}}$。对此近似解与数值解对比得出：从扩散开始，一直到最终稳态的过程中，稳态近似法获得的结果和精确解是同步的；稳态近似法获得的结果与接近最终稳态的情形吻合程度好，与远离最终稳态的情形吻合程度差些；稳态近似法获得的结果基本上满足总体质量守恒。