2. 清华大学 机械工程系, 北京 100084;
3. 后勤工程学院 军事油料应用与管理工程系, 重庆 401311
2. Department of Mechanical Engineering, Tsinghua University, Beijing 100084, China;
3. Department of POL Application & Management Engineering, Logistics Engineering University, Chongqing 401311, China
轮齿啮合过程中,由于齿根处应力过大以及齿根受交变应力作用引起的疲劳裂纹是轮齿弯曲折断破坏的主要原因之一,因此准确计算啮合过程中齿根弯曲应力的大小及分布显得尤为重要。交错轴变厚齿轮传动理论上可以在任意角度间进行运动及动力传递,然而由于渐开线变厚齿轮不同的端截面上具有不同的变位系数及齿根厚度,且配对变厚齿轮也具有不同的螺旋角及节锥角,因此传统的以悬臂梁理论为基础的材料力学法以及以保角映射理论为基础的弹性力学齿根应力计算方法均存在较大的计算误差。
目前国内外学者对于渐开线变厚齿轮传动进行了一定的研究。Tsai[1]、Innocenti[2]、Christopher[3]以及国内的吴序堂[4]、李瑰贤[5]、朱才朝等[6-10]对变厚齿轮传动的齿面创成、几何设计、加工方法及啮合特性等方面进行了大量的研究。在渐开线变厚齿轮齿根应力分析研究方面,Tsai等[11]对平行轴直齿变厚齿轮齿根应力的分布特性进行了研究并与实验测试结果进行了对比,钱学毅等[12]对典型平行轴直齿变厚齿轮在交变载荷作用下的齿根弯曲应力进行了研究。综上所述,目前传统理论对变厚齿轮传动齿根弯曲应力的求解计算繁琐,精度低,且研究主要局限于啮合接触形式仍为理论线啮合的平行轴直齿变厚齿轮,而对于渐开线斜齿变厚齿轮,尤其是理论啮合形式为点啮合的空间交错轴渐开线变厚齿轮传动齿根弯曲应力方面的研究,尚未见相关报道。
笔者基于空间齿轮啮合原理,对渐开线变厚齿轮齿根及过渡圆弧进行精确建模,采用有限元数值计算方法对轮齿啮合过程中齿根应力的分布规律展开研究,分析了齿根关键设计参数、载荷变化以及典型安装误差对齿根弯曲应力分布的影响规律。
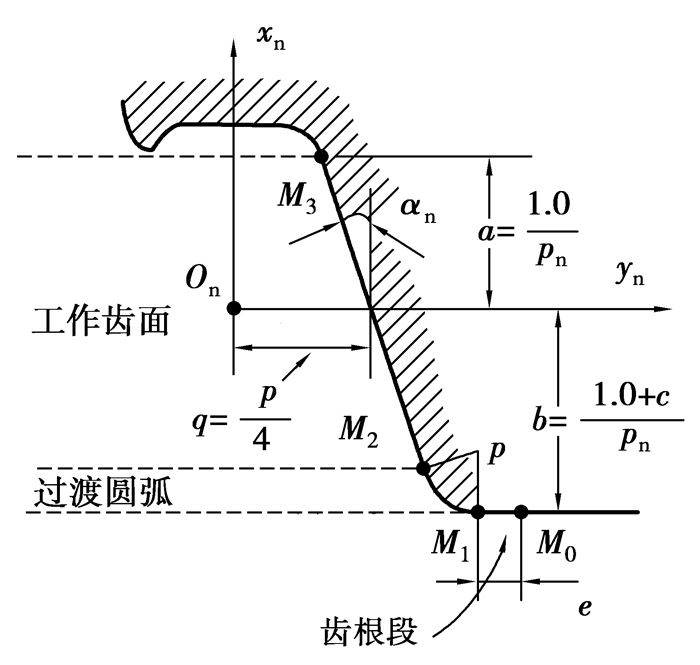
1 基于准确建模的变厚齿轮齿根模型基于Merritt的展成思想,对于滚齿加工变厚齿轮过程可以理解为假想齿条刀具的创成过程。图 1所示为Sn(xn, yn, zn)坐标系下齿条刀具法向截面简图,αn为齿条刀具齿形角,Pn为齿轮径节,p为齿轮周节,c为顶隙系数,ρ为齿条刀具圆角半径。刀具直线段M0M1和圆弧段M1M2分别对应加工齿轮的齿根段和过渡圆弧,直接影响齿轮根部几何尺寸参数。
|
图 1 齿条刀具法向截面 |
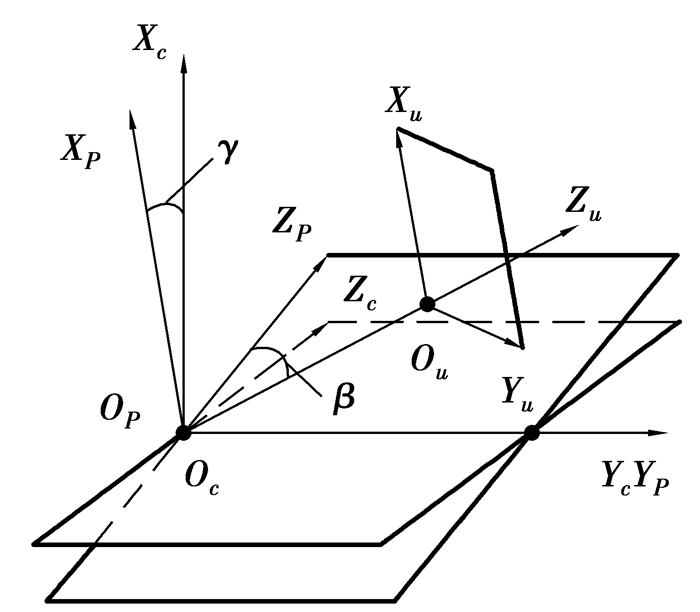
建立齿条刀具坐标系如图 2所示,其中YP-ZP为齿条刀具的节面。为了模拟变厚齿轮滚削过程,齿条刀具节面与坐标平面Yc-Zc间倾斜角γ为节锥角,β为齿线倾斜角。对于齿根与过渡圆弧段,由齿面几何参数定义有
| $ e = \frac{{{m_{\rm{n}}}{\rm{ \mathsf{ π} }}}}{4} - {m_{\rm{n}}}\tan {\alpha _{\rm{n}}} - \frac{{c{m_{\rm{n}}}\cos {\alpha _{\rm{n}}}}}{{1 - \sin {\alpha _{\rm{n}}}}}, $ | (1) |
|
图 2 齿条刀具坐标系Su、SP、Sc |
式中mn为齿轮法向模数。
当e=0时齿轮齿根段全部由过渡圆弧段代替,则有
| $ {c_{\rm{max}}} = \left( {\frac{{{m_{\rm{n}}}{\rm{ \mathsf{ π} }}}}{2} - 2{m_{\rm{n}}}\tan {\alpha _{\rm{n}}}} \right)\frac{{\left( {1 - \sin {\alpha _{\rm{n}}}} \right)}}{{2{m_{\rm{n}}}\cos {\alpha _{\rm{n}}}}}。$ | (2) |
在坐标系Sc(Xc, Yc, Zc)中刀具齿面可以通过下列坐标变换得到
| $ {\mathit{\boldsymbol{R}}_c} = {\mathit{\boldsymbol{M}}_{cp}}{\mathit{\boldsymbol{M}}_{pu}}{\mathit{\boldsymbol{R}}_u}, $ | (3) |
式中:Rc、Ru分别为齿条刀具齿面在Sc和Su的位置向量,Mpu和Mcp分别为坐标系Sp到Su和Sc到Sp的坐标变换矩阵。
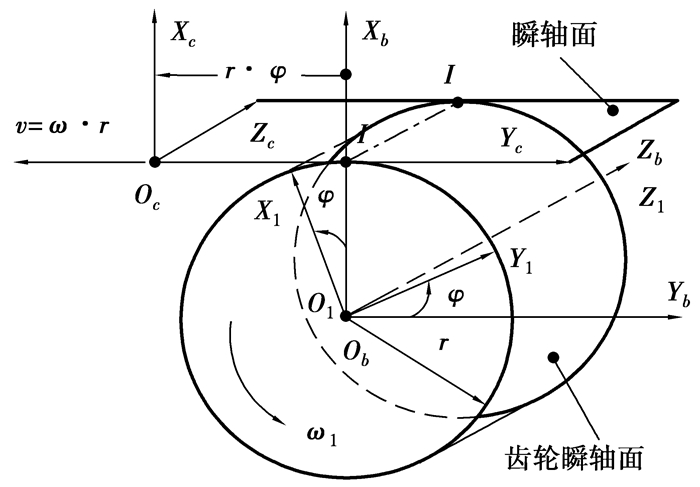
齿条刀具加工过程中,齿轮齿形R是齿条刀具齿形族Rc的包络加工成的,该包络表示在被加工齿轮刚性固连的坐标系S1(X1, Y1, Z1)中,如图 3所示为齿条刀具到被加工变厚齿轮间的坐标变换关系。
|
图 3 齿条刀具到变厚齿轮坐标系关系 |
其中Sb(Xb, Yb, Zb)为固定坐标系,S1(X1, Y1, Z1)为变厚齿轮所在坐标系, r为齿轮参考节圆半径,齿轮旋转角速度为ω,齿条刀具速度为v=ω·r,φ为变厚齿轮在加工过程中转过的角度。则有被加工变厚齿轮齿面位置向量与单位法向量为
| $ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{M}}_{1c}}{\mathit{\boldsymbol{R}}_c}, $ | (4) |
| $ \mathit{\boldsymbol{n}} = {\mathit{\boldsymbol{L}}_{1c}}{n_c}, $ | (5) |
式中:M1c为坐标系S1到Sc的坐标变换矩阵;L1c为坐标系S1到Sc的方向余弦变换矩阵;nc为坐标系Sc下刀具齿面的方向余弦;n为坐标系S1下变厚齿轮齿面的方向余弦。
基于空间啮合原理,得到齿轮加工啮合方程为
| $ \varphi {\rm{ = }}\left( {{n_{xc}}{y_c} - {n_{yc}}{x_c}} \right)/{n_{xc}}r, $ | (6) |
式中:nxc、nyc为坐标系Sc下接触点沿x、y方向余弦;xc、yc为坐标系Sc下接触点位置坐标。
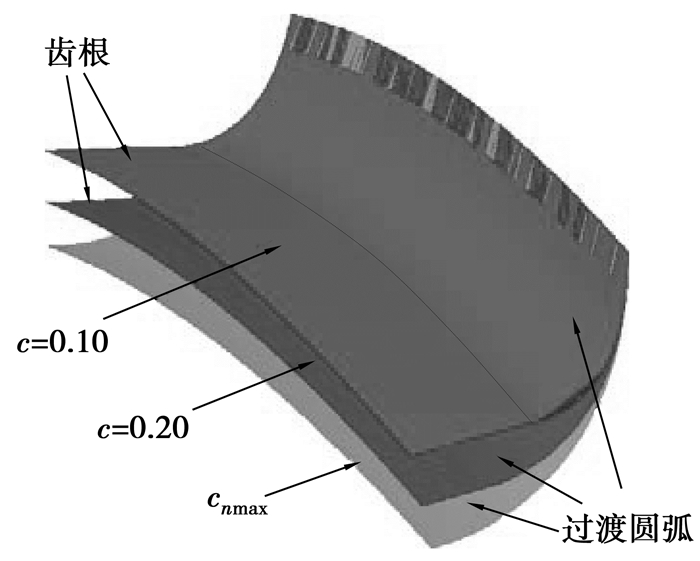
联立式(4)与式(6),则可以得到加工后的变厚齿轮齿面方程。编制Matlab计算程序得到渐开线变厚齿轮齿面位置坐标及法向量,得到齿面点云数据,经过三维逆向得到不同顶隙系数下准确的变厚齿轮齿面模型,其中齿根与过渡圆弧如图 4所示。
|
图 4 渐开线变厚齿轮齿根模型 |
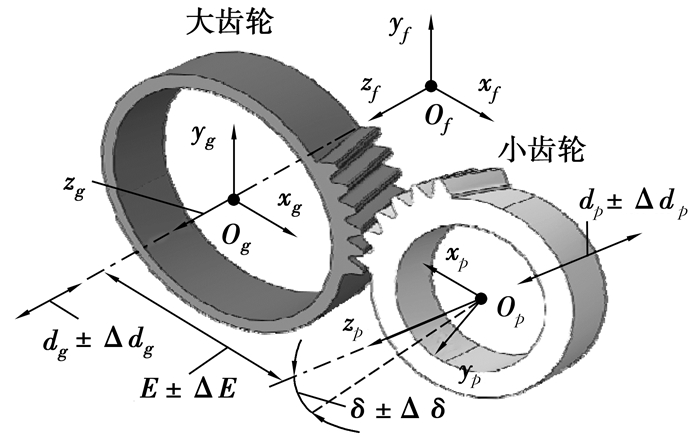
建立考虑实际安装误差的小角度交错轴空间啮合坐标系如图 5所示,其中Sf(xf, yf, zf)为全局坐标系;Sp(xp, yp, zp)与Sg(xg, yg, zg)分别固连于小齿轮与大齿轮;Of、Op与Og分别为对应坐标系的原点;E为中心距;δ为轴交角;dp与dg分别为小齿轮与大齿轮的轴向安装距;ΔE、Δδ、Δdp与Δdg分别为中心距误差,轴交角误差,小齿轮轴向位置误差与大齿轮轴向位置误差。
|
图 5 考虑安装误差的小角度交错轴变厚齿轮实体装配模型 |
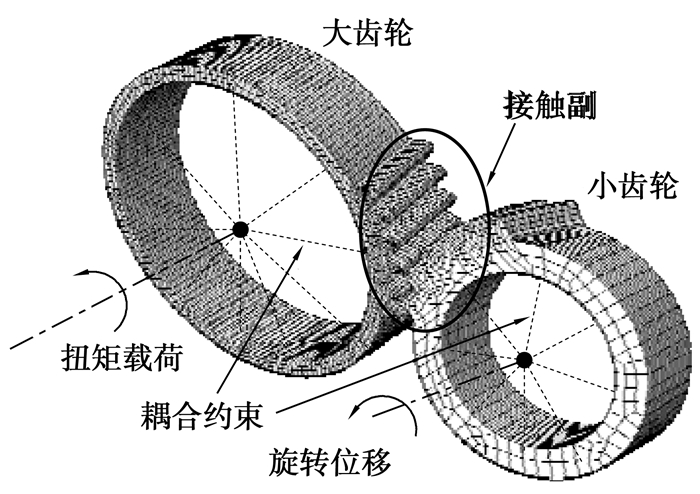
基于有限元法,对交错轴渐开线变厚齿轮副实体模型进行网格离散,建立啮合齿面间的接触副,通过耦合约束对小齿轮与大齿轮分别施加旋转位移与扭转载荷边界,得到小角度交错轴变厚齿轮接触有限元模型如图 6所示,仿真齿轮系统参数如表 1所示。
|
图 6 小角度交错轴变厚齿轮有限元模型 |
| 表 1 齿轮系统参数 |
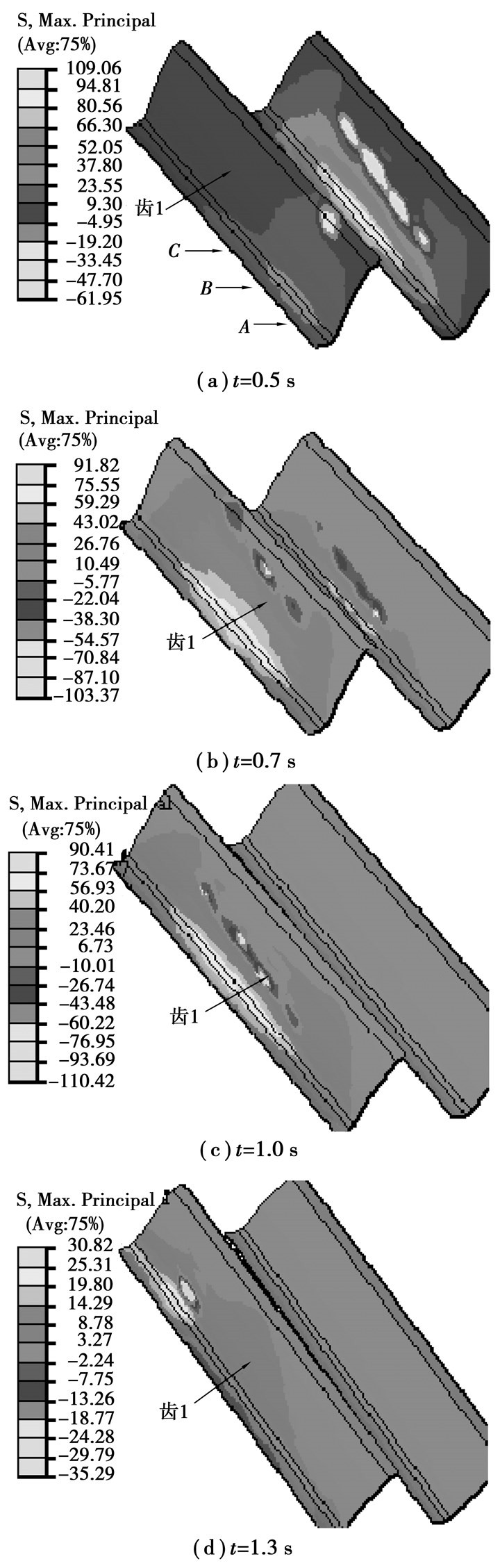
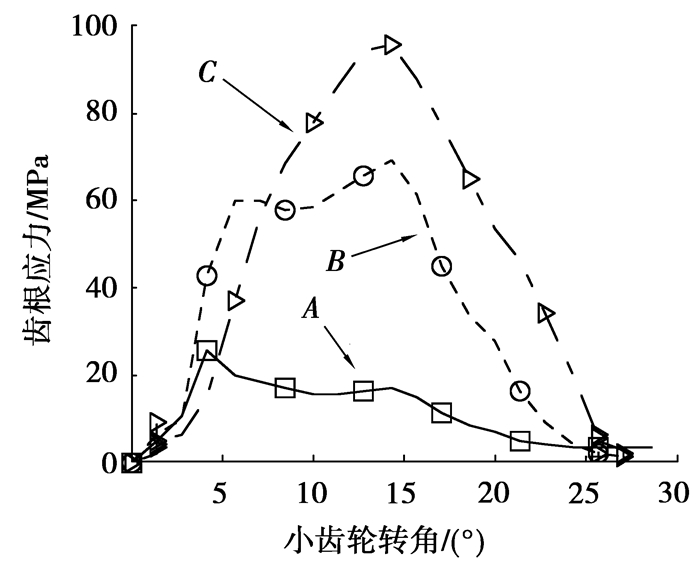
图 7所示为额定载荷2 000 N·m,理想无安装误差工况下大齿轮齿面不同时刻的弯曲应力分布云图。图 8所示为齿1上A、B、C3个关键位置一个啮合周期内弯曲应力变化图。从图中可以看出,交错轴变厚齿轮弯曲应力分布呈椭圆状,明显区别于普通渐开线直齿轮与斜齿轮的线型分布;随着轮齿的啮合,齿根弯曲应力的分布从轮齿一端沿齿宽方向向另外一端偏移,承受较大弯曲应力的区域的变化呈现由小变大再变小的趋势。轮齿啮合过程中最大齿根应力出现在C点轮齿的中间位置。
|
图 7 齿根弯曲应力云图分布 |
|
图 8 啮合周期内不同位置齿根应力变化 |
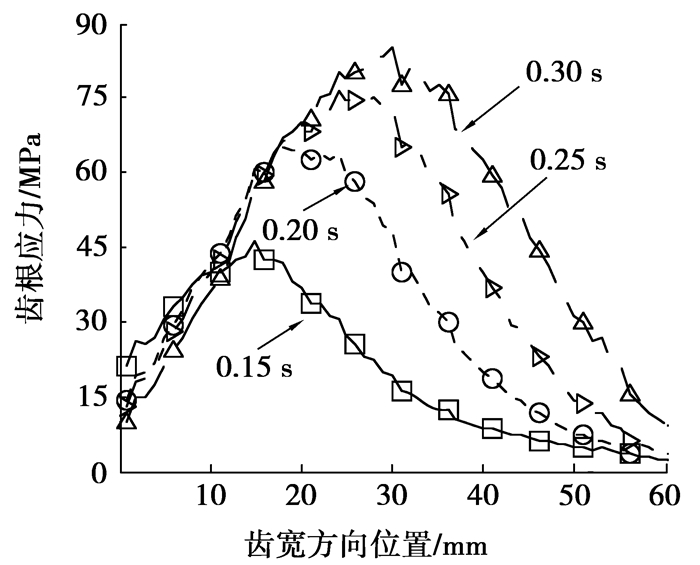
图 9为一个啮合周期内不同时刻沿齿宽方向分布的弯曲应力图。从图中可以明显看出轮齿啮合过程中,齿面的最大弯曲应力从齿面一端向中间移动。
|
图 9 沿齿宽方向一个啮合周期内齿根弯曲应力分布 |
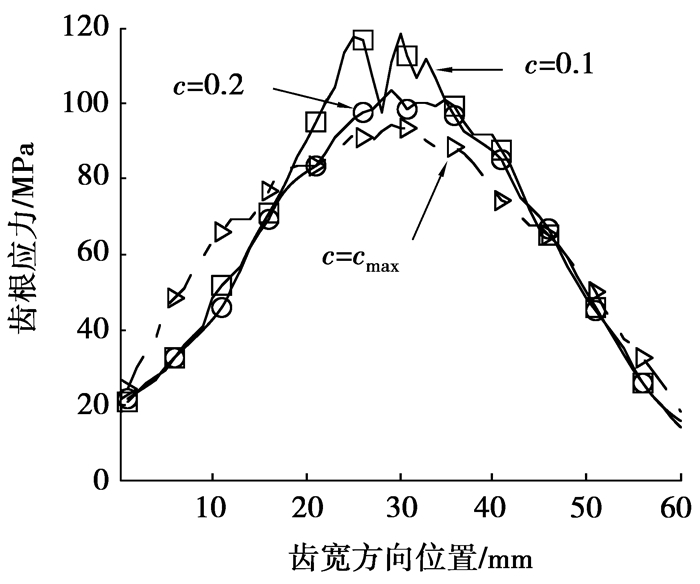
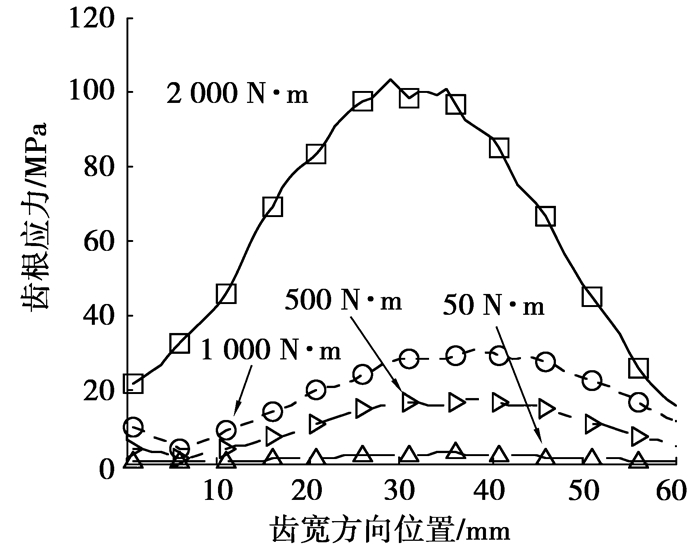
图 10所示为不同顶隙系数工况下,齿根应力分布曲线。图 11所示为扭矩载荷对齿根应力的影响。
|
图 10 顶隙系数对齿根应力的影响 |
|
图 11 外部载荷对齿根应力的影响 |
从计算结果可以看出,顶隙系数对齿根弯曲应力有较大的影响,随着c值从0.1增加到cmax,齿根弯曲应力的最大值从120 MPa减少到90 MPa,且弯曲应力在齿宽方向上的分布更加平坦。轻载情况下,齿根应力在齿宽方向的分布较为平坦,但随着载荷的增加,轮齿整体齿根应力水平增加明显,且轮齿中间位置的应力值逐渐高于轮齿两端的应力值,分布曲线呈抛物线状。
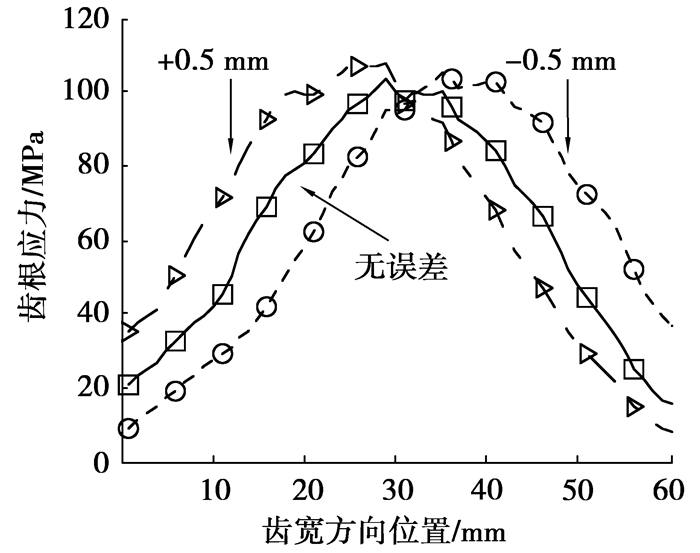
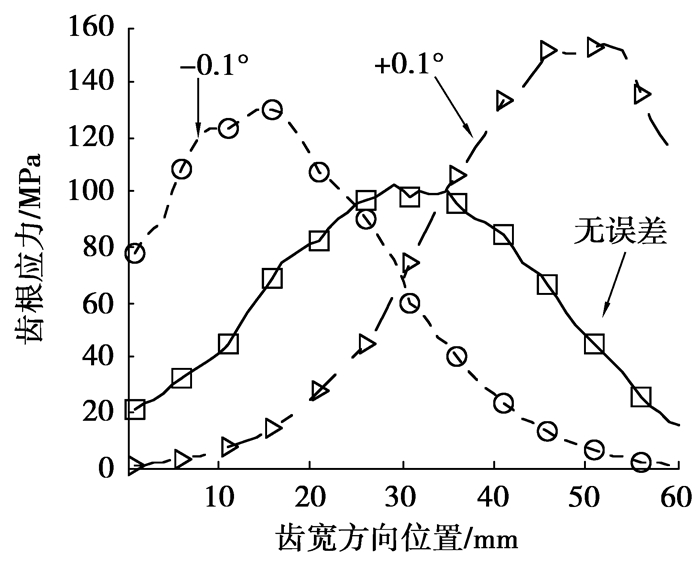
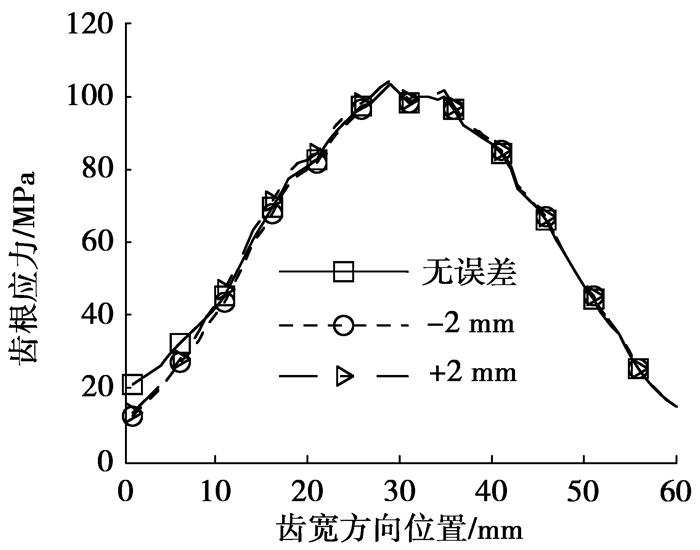
3.2 安装误差对齿根应力的影响图 12~15为安装误差对轮齿齿根应力的影响。从图中可以看出,±0.5 mm的中心距安装误差对齿宽方向最大齿根应力的分布产生了一定影响,使得最大弯曲应力值有所增加,且正负中心距安装误差的存在使得最大弯曲应力的位置分别向轮齿两端发生偏移。±0.1°轴交角误差的存在对齿根弯曲应力分布产生了较大的影响,轴交角正负误差的存在使得齿宽方向最大齿根应力值从90 MPa增加到了150 MPa,且最大弯曲应力的分布位置沿齿宽方向向轮齿两端发生了较大的偏移。±2 mm的小齿轮轴向位置误差与大齿轮轴向位置误差的存在对齿跟应力的分布并影响较小,与中心距误差和轴交角误差的影响比较,轴向位置误差的影响基本可以忽略。
|
图 12 中心距误差对齿根应力的影响 |
|
图 13 轴交角误差对齿根应力的影响 |

|
图 14 小齿轮轴向位置误差对齿根应力的影响 |
|
图 15 大齿轮轴向位置误差对齿根应力的影响 |
采用空间齿轮加工原理及有限单元法,提出了基于齿根及过渡圆弧精确建模的渐开线交错轴变厚齿轮齿根弯曲应力数值计算方法,对轮齿啮合过程中,齿根应力的分布规律展开研究得到如下结论:
1) 交错轴渐开线变厚齿轮齿跟应力呈明显区别于普通渐开线直齿轮的椭圆状分布,且啮合过程中,最大齿根弯曲应力从轮齿一端沿齿宽方向向另外一端偏移。
2) 随着顶隙系数的增加,齿根最大弯曲应力减小;轻载下齿宽方向的齿根应力分布较为平坦,重载下齿宽方向的齿根应力呈明显的抛物线状,最大齿根应力分布于轮齿中间部位。
3) 轴交角误差和中心距误差的存在使得最大齿根弯曲应力增大,最大弯曲应力的位置随误差的正负而分别向轮齿的两端偏移,大小齿轮轴向位置误差对轮齿弯曲应力影响较小。
| [1] | Wu S H, Tsai S J. Contact stress analysis of skew conical involute gear drives in approximate line contact[J]. Mechanism and Machine Theory, 2009, 44(9): 1658–1676. DOI:10.1016/j.mechmachtheory.2009.01.010 |
| [2] | Innocenti C. The kinematics of conical involute gear hobbing[C]//Proceedings of the ASME International Mechanical Engineering Congress and Exposition, November 11-15, 2007, Washington, USA. USA:Design and Manufacturing, 2007, 3:415-424. |
| [3] | Traut C, Binz H, Bachmann M. The influence of manufacturing deviations on the transmission behavior of conical involute gears[C]//Proceedings of the International Conference on Gears-Europe invites the world, October 4-6, 2010, Garching, Germany.[S.l.]:Society for Product and Process Design, 2010:647-658. |
| [4] |
贺敬良, 吴序堂.
交错轴渐开线锥形齿轮副啮合原理研究[J]. 机械工程学报, 2004, 40(4): 81–84.
HE Jingliang, WU Xutang. Study on gearing principle of crossed-axes conical involute gears[J]. Chinese Journal of Mechanical Engineering, 2004, 40(4): 81–84. (in Chinese) |
| [5] | Li G X, Wen J M, Li X, et al. Meshing theory and simulation of noninvolute beveloid gears[J]. Mechanism and Machine Theory, 2004, 39(8): 883–892. DOI:10.1016/j.mechmachtheory.2004.02.005 |
| [6] | Song C S, Zhu C C, Liu W J. Sliding friction effect on dynamics of crossed beveloid gears with small shaft angle[J]. Journal of Mechanical Science and Technology, 2013, 27(5): 1255–1263. DOI:10.1007/s12206-013-0309-2 |
| [7] | Zhu C C, Song C S, Lim T C, et al. Geometry design and tooth contact analysis of crossed beveloid gears for marine transmissions[J]. Chinese Journal of Mechanical Engineering, 2012, 25(2): 328–337. DOI:10.3901/CJME.2012.02.328 |
| [8] | Song C S, Zhu C C, Lim T C, et al. Parametric analysis of gear mesh and dynamic response of loaded helical beveloid transmission with small shaft angle[J]. Journal of Mechanical Design, 2012, 134(8): 1–8. |
| [9] |
宋朝省, 朱才朝, 刘立斌, 等.
交错轴渐开线变厚齿轮传动节圆锥设计[J]. 重庆大学学报, 2012, 35(8): 48–53.
SONG Chaosheng, ZHU Caichao, LIU Libin, et al. Research on pitch cone design for beveloid gears with crossed axes[J]. Journal of Chongqing University, 2012, 35(8): 48–53. DOI:10.11835/j.issn.1000-582X.2012.08.009 (in Chinese) |
| [10] |
宋朝省, 朱才朝, LIMT C, 等.
小角度空间交错轴变厚齿轮传动啮合动态特性研究[J]. 振动与冲击, 2012, 31(8): 153–157.
SONG Chaosherng, ZHU Caichao, LIM Teik Chin, et al. Time-varying mesh characteristics of beveloid gears with crossed axes and small shaft angle[J]. Journal of Vibration and Shock, 2012, 31(8): 153–157. (in Chinese) |
| [11] | Tsai S J, W S H, DI-Berichte Gmbh V. Experimental and numerical root stress analysis of conical gears[C]//Proceedings of the International Conference on Gears-Europe invites the world, September 14-16, 2005, München, Germany.[S.l.]:Society for Product and Process Design, 2005:1127-1144. |
| [12] |
钱学毅, 吴双.
变齿厚渐开线齿轮齿根弯曲应力研究[J]. 黑龙江工程学院学报:自然科学版, 2010, 24(4): 55–58.
QIAN Xueyi, WU Shuang. Study of bending stress of dedendum of variable tooth thickness involute gear[J]. Journal of Heilongjiang Institute of Technology:Natural Science, 2010, 24(4): 55–58. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

