机械产品由于裂纹缺陷的存在,往往寿命低,故障率高,直接导致生产率低[1-4],其中构件断裂是造成各种机械恶性事故的重要原因[5-7],而构件在使用过程中产生的裂纹是造成构件断裂的主要原因,因此,如何抑制金属构件中裂纹的萌生和扩展越来越受到人们的关注。电磁热效应裂纹止裂技术不但方法简单,收效迅速,而且对构件整体不造成破坏[8-9]。通电电流在裂纹附近产生绕流集中效应,所生成的焦耳热源使裂尖处温度瞬时急剧升高,能够在很小的范围内使裂尖熔化,形成微小的焊口,从而增大了裂纹前缘的曲率半径,显著降低了应力集中,有效地遏制了裂纹的扩展[10-12]。目前,国内外学者对圆形裂纹、椭圆形裂纹及单边裂纹等的温度场进行了相关分析[13-14],但是对实际应用中的多裂纹问题研究较少。笔者研究了双半圆形埋藏裂纹,裂纹形状不同造成温度场分布的不同,并且计算了两个裂纹温度场之间的相互热影响,为电磁热效应裂纹止裂技术的应用提供参考。
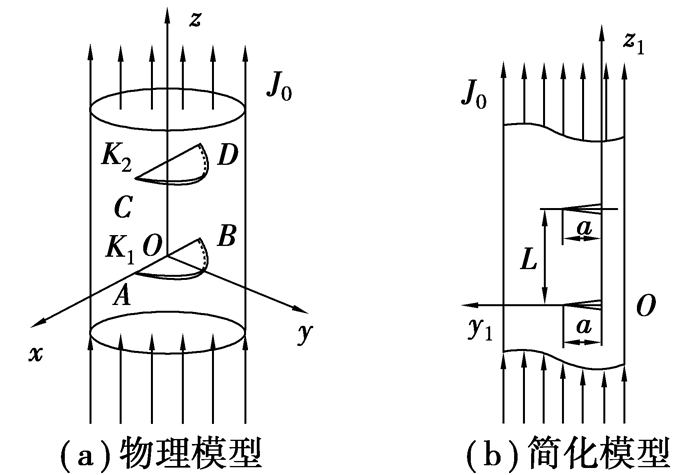
1 金属构件内电流密度的分布如图 1(a)所示为带有半圆形埋藏裂纹的圆柱形金属构件的计算模型,LAB为裂纹尖端,沿垂直xoy面通入电流密度为J0的均匀强脉冲电流。由于金属构件中存在裂纹且裂纹不导电,电流会在裂纹处产生强烈的绕流和集中现象,电能转化成热能,从而导致此处的材料温度急剧升高。此时电流发出的热相当于在裂尖处作用了一个线热源。由于电流绕半圆周方向的绕流相比较沿直径方向的绕流要小得多,假设在建立模型计算时忽略电流沿半圆周方向的绕流,只考虑电流沿直径方向的绕流,在计算中平行于xoz面切取单位厚度的轴切面切片如图 1(b),转化成平面上存在一个点热源的问题[15],对其求解可得出该点热源对空间任意一点温度的影响,对其在整个裂纹尖端积分可得出含半圆形埋藏裂纹的圆柱模型的温度场分布。
|
图 1 含半圆形埋藏裂纹的金属构件 |
裂尖处x、y方向的电流分量分别为[16]
| $ {j_{{y_1}}}^2 = {J_0}^2 \cdot \\ \left[\begin{array}{l} \frac{{\left( {{z_1}^2- {y_1}^2} \right)\left( {{z_1}^2- {y_1}^2 + {a^2}} \right) + 4{y_1}^2{z_1}^2}}{{2\left( {{z_1}^2- {y_1}^2 + {a^2}} \right) + 8{y_1}^2{z_1}^2}}\\ + \frac{{\sqrt {\left[{\left( {{z_1}^2-{y_1}^2} \right)\left( {{z_1}^2-{y_1}^2 + {a^2}} \right) + 4{y_1}^2{z_1}^2} \right] + {{\left( {2{y_1}{z_1}{a^2}} \right)}^2}} }}{{2\left( {{z_1}^2 -{y_1}^2 + {a^2}} \right) + 8{y_1}^2{z_1}^2}} \end{array} \right], \\{j_{{z_1}}}^2 = {J_0}^2 \cdot \\ \left[\begin{array}{l} \frac{{- \left( {{z_1}^2- {y_1}^2} \right)\left( {{z_1}^2- {y_1}^2 + {a^2}} \right) - 4{y_1}^2{z_1}^2}}{{2\left( {{z_1}^2 - {y_1}^2 + {a^2}} \right) + 8{y_1}^2{z_1}^2}}\\ + \frac{{\sqrt {\left[{\left( {{z_1}^2-{y_1}^2} \right)\left( {{z_1}^2-{y_1}^2 + {a^2}} \right) + 4{y_1}^2{z_1}^2} \right] + {{\left( {2{y_1}{z_1}{a^2}} \right)}^2}} }}{{2\left( {{z_1}^2 -{y_1}^2 + {a^2}} \right) + 8{y_1}^2{z_1}^2}} \end{array} \right], $ | (1) |
式中:J0是随时间变化的电流密度,A/m2;jy1、jz1分别为电流密度在y1、z1方向的分量,A/m2; a为裂纹长度,m。
由热源功率密度公式,并将式(1)代入得
| $ \begin{array}{l} P\left( {{y_1}, {z_1}} \right) = \frac{{{j_{{y_1}}}^2 + {j_{{z_1}}}^2}}{{{\sigma ^*}}}\\ = \frac{{{J_0}}}{{{\sigma ^*}}} \times \frac{{{y_1}^2 + {z_1}^2}}{{\sqrt {{{\left( {{y_1}^2 + {z_1}^2} \right)}^2} - 2{a^2}\left( {{y_1}^2 - {z_1}^2} \right) + {a^4}} }}, \end{array} $ | (2) |
式中σ*为电导率, (Ω·m)-1。
转换坐标系,令z1=rcos θ,
y1=a+rsin θ,化为极坐标有
| $ \begin{array}{l} P\left( {{y_1}, {z_1}} \right) = p\left( {r, \theta } \right)\\ = \frac{{{J_0}^2}}{{{\sigma ^*}}} \cdot \frac{{{a^2} + 2ar\sin \theta + {r^2}}}{{r\sqrt {4{a^2} + 4ar\sin \theta + {r^2}} }}。\end{array} $ | (3) |
由于通电瞬时脉冲电流在裂尖附近形成绕流,产生的热量远大于在其余地方产生的热量,所以可将围绕裂尖半径为r0且r0«a的圆形区域内单位时间内产生的热量简化成一个点热源[17],可求得裂尖处的点热源产生的热量Q的强度,由焦耳定律可得
| $ \begin{array}{*{20}{l}} {Q{\rm{ = }}\int {q{\rm{d}}s} = \int_0^{{r_0}} {2{\rm{ \mathsf{ π} }}r \cdot p\left( {r,\theta } \right){\rm{d}}r} }\\ { = \frac{{{J_0}^2}}{{{\sigma ^*}}}\int_0^{{r_0}} {2{\rm{ \mathsf{ π} }}r \cdot \frac{{{a^2} + 2ar\sin \theta + {r^2}}}{{r\sqrt {4{a^2} + 4ar\sin \theta + {r^2}} }}{\rm{d}}r} }。\end{array} $ | (4) |
因为r«a所以简化点热源在裂尖处产生的热量
| $ \begin{array}{*{20}{l}} {Q = \frac{{{J_0}^2}}{{{\sigma ^*}}}\int_0^{{r_0}} {2{\rm{ \mathsf{ π} }}r\frac{{{a^2} + 2ar\sin \theta + {r^2}}}{{r\sqrt {4{a^2} + 4ar\sin \theta + {r^2}} }}{\rm{d}}r} }\\ { = \frac{{{J_0}^2}}{{{\sigma ^*}}}\int_0^{{r_0}} {2{\rm{ \mathsf{ π} }}r\frac{{{a^2}}}{{r\sqrt {4{a^2}} }}{\rm{d}}r} = \frac{{{J_0}^2{\rm{ \mathsf{ π} }}a{r_0}}}{{{\sigma ^*}}}}。\end{array} $ | (5) |
由于在实际生产中,裂纹相对于工件来讲很小,因此可以把裂尖处线热源看做是一个有限长瞬时线热源来计算。
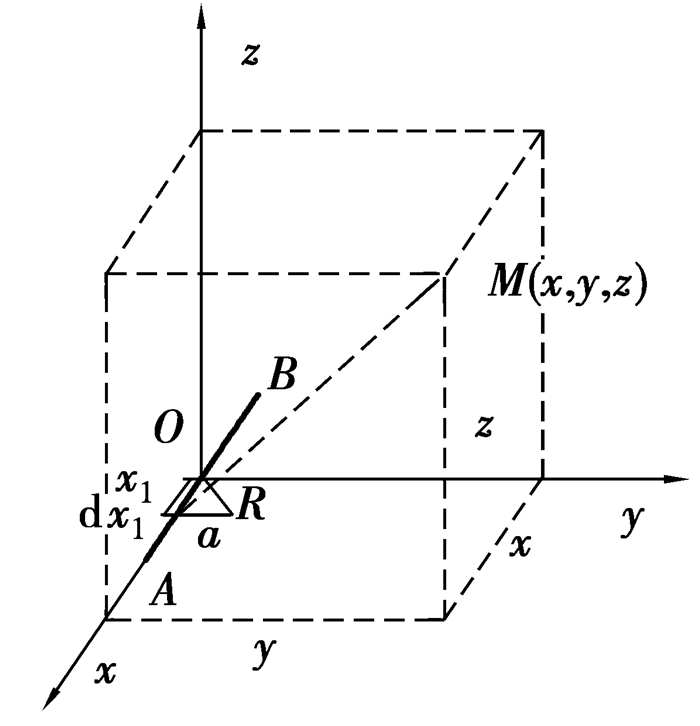
如图 2温度场坐标,先观察任一个单元线段热源dx1的影响,dx1单元线热源可看作是一个点热源,其发热量为Qdx1,这一单元线热源在时间t内对任意一点M(x, y, z, t)作用所产生的温度场为[18-19]
| $ \begin{array}{*{20}{l}} {T\left( {x,y,z,t} \right) = \frac{{Q{\rm{d}}{x_1}}}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{c_p}\rho }} \cdot }\\ {\exp \left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2} + {y^2} + {z^2}}}{{4at}}} \right],} \end{array} $ | (6) |
|
图 2 温度场坐标 |
式中:α为表面传热系数, W/(m2·K); cp为质量定压热容, J/(kg·℃); ρ为密度, kg/m2; t为放电时间, s。则整个裂纹线热源对M点所引起的总的温度场为
| $ \begin{array}{*{20}{l}} {T\left( {x,y,z,t} \right) = \int_{ - R}^R {\frac{Q}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{C_p}\rho }}} \cdot }\\ {{{\rm{e}}^{\left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2} + {y^2} + {z^2}}}{{4at}}} \right]}}{\rm{d}}{x_1}}。\end{array} $ | (7) |
将式(5)带入式(7)可得
| $ \begin{array}{*{20}{l}} {T\left( {x,y,z,t} \right) = \int_{ - R}^R {\frac{{{J_0}^2{\rm{ \mathit{ π} }}a{r_0}}}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{C_p}\rho {\sigma ^*}}}} }\\ { \cdot {{\rm{e}}^{\left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2} + {y^2} + {z^2}}}{{4at}}} \right]}}{\rm{d}}{x_1}}\\ { = \int_0^{\frac{{{\rm{ \mathit{ π} }}}}{2}} {\frac{{2{R^2}{J_0}^2{\rm{ \mathit{ π} }}{r_0}{{\sin }^2}\theta }}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{C_p}\rho {\sigma ^*}}} \cdot {{\rm{e}}^{\left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2} + {y^2} + {z^2}}}{{4at}}} \right]}}{\rm{d}}\theta } ,} \end{array} $ | (8) |
式中:R为半圆形裂纹的半径,m;θ为x1与半径R的夹角。
考虑脉冲放电瞬间裂尖AB产生的温度场对裂尖CD温度场的影响,取裂尖AB上一点N(x1, 0, 0),其对应裂尖CD上的点为N1(x, 0, L), 则裂尖AB对点N1(x, 0, L)的温度场影响为
| $ \begin{array}{*{20}{l}} {T\left( {x,y,z,t} \right) = \int_{ - R}^R {\frac{{{J_0}^2{\rm{ \mathit{ π} }}a{r_0}}}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{C_p}\rho {\sigma ^*}}}} }\\ { \cdot {{\rm{e}}^{\left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2} + {y^2} + {L^2}}}{{4at}}} \right]}}{\rm{d}}{x_1}}。\end{array} $ |
脉冲放电时点N1(x, 0, L)产生的温度场为
| $ \begin{array}{*{20}{l}} {{T_2}\left( {x,y,z,t} \right) = \int_{ - R}^R {\frac{{{J_0}^2{\rm{ \mathit{ π} }}a{r_0}}}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{C_p}\rho {\sigma ^*}}}} }\\ { \cdot {{\rm{e}}^{\left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2}}}{{4at}}} \right]}}{\rm{d}}{x_1}}。\end{array} $ |
设温度场之比为I, 则
| $ \begin{array}{*{20}{l}} {I = \frac{{{T_1}}}{{{T_2}}}}\\ { = \frac{{\int_{ - R}^R {\frac{{{J_0}^2{\rm{ \mathit{ π} }}a{r_0}}}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{C_p}\rho {\sigma ^*}}}} {{\rm{e}}^{\left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2} + {L^2}}}{{4at}}} \right]}}{\rm{d}}{x_1}}}{{\int_{ - R}^R {\frac{{{J_0}^2{\rm{ \mathit{ π} }}a{r_0}}}{{{{\left( {2\sqrt {{\rm{ \mathit{ π} }}at} } \right)}^3}{C_p}\rho {\sigma ^*}}}} \cdot {{\rm{e}}^{\left[ { - \frac{{{{\left( {x - {x_1}} \right)}^2}}}{{4at}}} \right]}}{\rm{d}}{x_1}}}}。\end{array} $ | (9) |
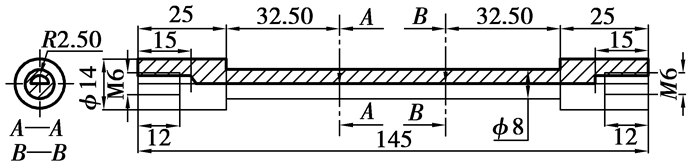
模型材料选用45#钢进行分析运算。圆柱形金属构件半径为R0=4.0×10-3 m,半圆形裂纹半径为R=2.5×10-3 m, 具体尺寸如图 3所示。向构件内沿z轴通入U=1 300 V的电压,通电时间t=2.5 μs。材料的各项物理属性为:熔点1 515 ℃,电导率σ*=7.5×106(Ω·m)-1,热传导系数为x=50.2 W/(m2·K),取r0=2.2×10-6 m,L=0.03 m。
|
图 3 构件尺寸 |
将数据代入公式(9)可得
I«1。
由此可得当L=0.03 m时,两个裂尖之间的相互热影响很小,可以忽略不计。在裂尖处局部加密划分网格如图 4所示。

|
图 4 有限单元网格模型 |
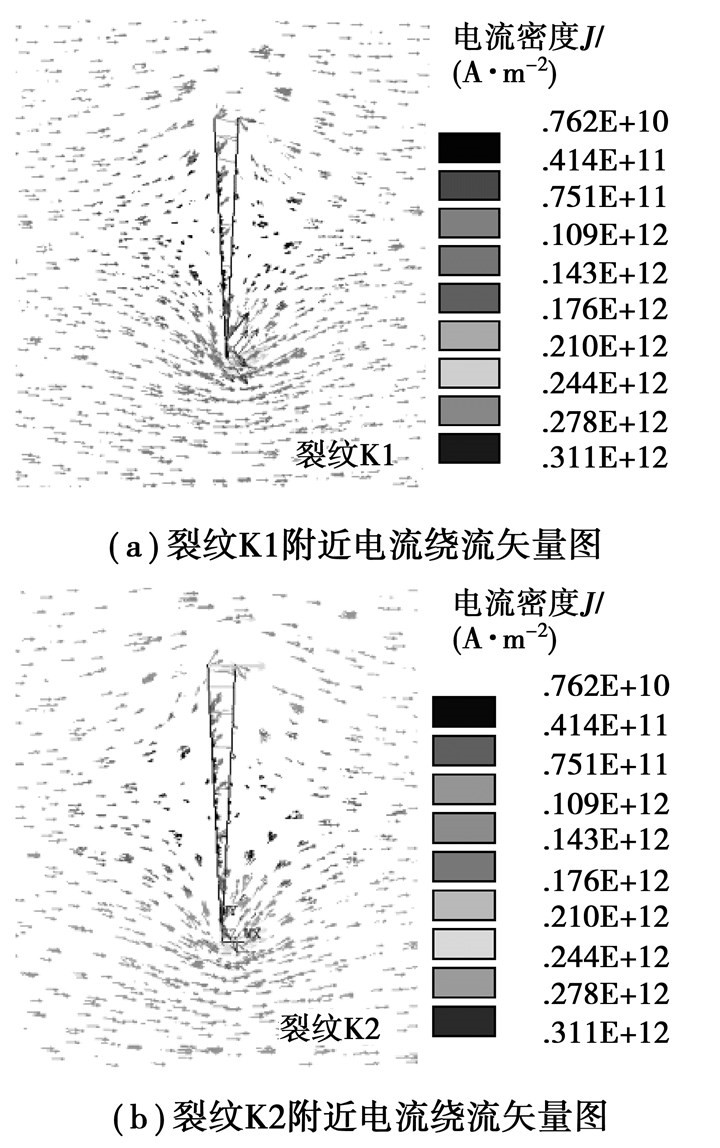
金属构件在通入强脉冲电流的瞬间,电流在裂纹处形成绕流引起温度场的变化,由于埋藏裂纹的形状导致电流在裂纹各处的电流密度大小不同,最终导致金属试件中的温度呈现不同的分布情况。图 5分别为K1、K2两裂纹yoz面电流密度分布,由图可以直观地看出电流在裂纹尖端发生强烈的绕流现象,裂尖附近的电流密度较大,而在裂纹的其他部分绕流相对很小导致电流密度值较小。
|
图 5 yoz面电流密度分布 |
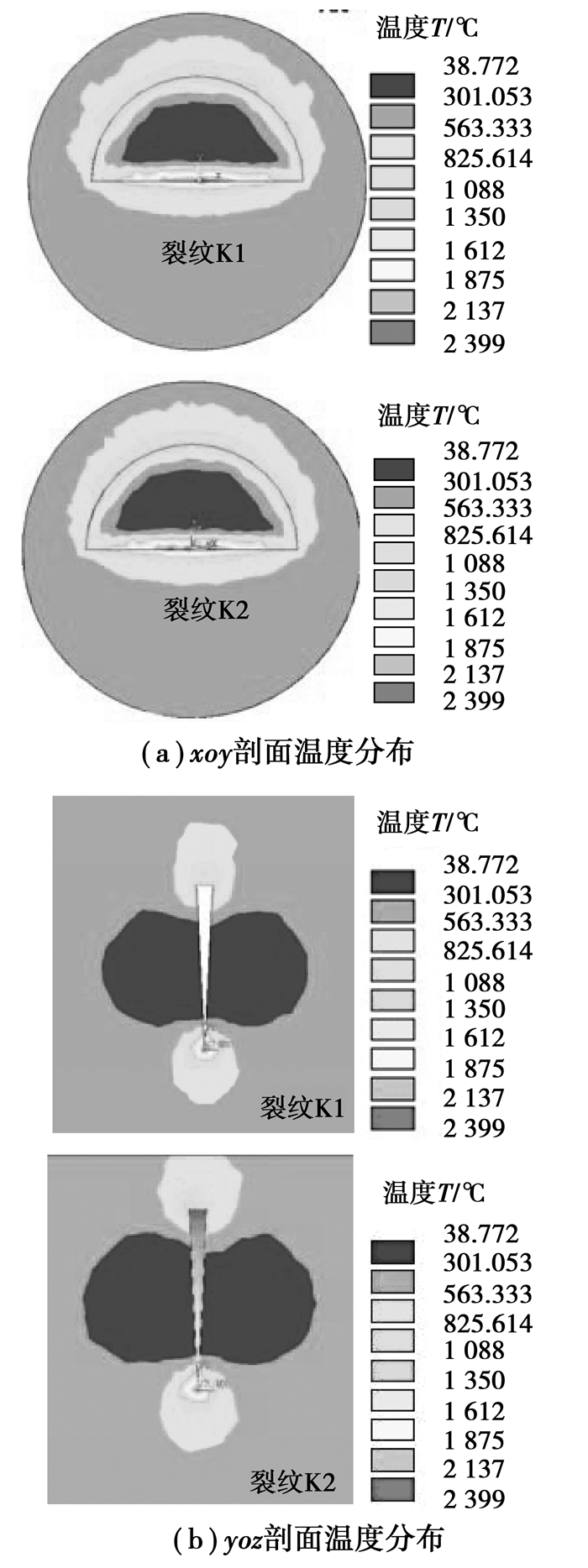
放电完成瞬间,金属构件温度场如图 6所示,温度最大值(在坐标原点处)为2 399.000 ℃,取与之相对应的电流密度J0=0.311×1012 A/m2代入温度场公式(8)进行计算,得最大温度Tmax=2 474.560 ℃,对照模拟数值的误差为75.560 ℃,相对误差为3.150 %。由此可知,理论计算与数值模拟结果相吻合。
|
图 6 温度场分布 |
制备试件材料选用45#钢,制备含有半圆形埋藏裂纹的试件。制备过程为,取45钢圆柱形材料,具体试件尺寸如图 3所示,在A、B位置车出半径为2.5 mm的槽,并用切割机切出半圆形裂纹如图 7(a)所示,紧接着把前面车出的槽焊接起来,再用车床把焊接的部位的半径车到4 mm,使其成为可放电试件,如图 7(b)所示。

|
图 7 试件实物图 |
实验设备选用的是ZL-2型超强脉冲电流发生装置,设备实物如图 8所示,具有完整的安全防范措施,可以在大范围调节电流和电压,并通过调节电容间的串、并联方式获得不同的瞬间脉冲电流值。该装置输出的放电电流的最大值为140 kA,放电周期的最小值为250 μs。

|
图 8 ZL-2型放电设备 |
采用6 300 V的放电电压进行实验过程中,通电瞬间伴有一声闷响,这是由于放电瞬间裂尖附近产生电流绕流进而产生热集中,使附近的金属熔化并在压应力作用下产生一声闷响。电流热效应集中在裂纹附近,且温度很高,甚至超出基材的熔点。
4.4 裂纹尖端形貌利用线切割机沿半埋藏裂纹的垂直方向进行切割取样,用砂纸磨光并在抛光机上抛光,最后用显微镜观察。如图 9所示为45#钢中的半圆形埋藏裂纹尖端的宏观形貌。由图可知,脉冲放电后裂尖变钝,裂尖有明显的熔化痕迹,围绕裂尖形成明显的热影响区,裂尖附近金属组织在瞬间加热和自激冷作用下,组织得到了细化,同时钝化的裂尖对裂纹的扩展起到了良好的屏蔽作用。

|
图 9 放电后裂尖宏观形貌 |
经脉冲放电后,一方面半埋藏裂尖发生熔化,释放了裂尖处集中的应力,消除了应力集中,抑制裂纹的进一步扩展;另一方面,由于电流绕流导致裂尖处与其他部位温度梯度较大,裂尖处有较大的膨胀量,与周围基体相互作用力增加,周围对裂尖的约束力大大加强,使其向裂纹内压缩,使裂纹面上的原子重新结合。裂尖钝化是阻止裂纹继续扩展的主要原因。
4 结论1) 通过理论分析推导出了脉冲放电瞬间裂纹附近绕流的电流密度分布规律和裂纹尖端附近温度场分布的表达式及两裂纹之间热影响关系。
2) 用ANSYS有限元软件建立了数值模型并对其进行了数值模拟,由理论计算与数值分析结果对比,两方法所得温度场分布规律一致。
3) 通过对含半圆形埋藏裂纹的45#钢试件进行脉冲放电,脉冲放电后裂尖变钝,裂尖有明显的熔化痕迹,围绕裂尖形成明显的热影响区。
| [1] |
王会强, 蒋辉, 邢艳秋, 等.
农业机械常见的失效分析[J]. 农机化研究, 2008, 9: 28–30.
WANG Huiqiang, JIANG Hui, XING Yanqiu, et al. The usual failure and analysis in agricultural machinery[J]. Journal of Agricultural Mechanization Research, 2008, 9: 28–30. DOI:10.3969/j.issn.1003-188X.2008.01.007 (in Chinese) |
| [2] |
王开建, 刘子东, 曲仁, 等.
农业机械失效典例分析初探[J]. 贵州大学学报:自然科学版, 2001, 18(2): 118–123.
WANG Kaijian, LIU Zidong, QU Ren, et al. Analysis and research of the typical example of product failure of agriculture machinery[J]. Journal of Guizhou University:Natural Science, 2001, 18(2): 118–123. (in Chinese) |
| [3] | Link R E, Roe C. Crack arrest testing using small wide plate SE(T) specimens[J]. Journal of ASTM International, 2009, 1502: 93–113. |
| [4] | Sbitti A, Taheri S. Crack arrest in high cycle thermal fatigue crazing[J]. Nuclear Engineering and Design, 2010, 240(1): 30–38. DOI:10.1016/j.nucengdes.2009.09.030 |
| [5] | Bai X D, Fu Y M. Advances in research on elect romagnetic heating effect s to stop crack propa2 gation in metal components[J]. International Journal of Nolinear Science and Numerical Simulation K, 2003, 9(1): 65–77. |
| [6] | 李永东. 理论与应用断裂力学[M]. 北京: 兵器工业出版社, 2005. |
| [7] | Shindo Y, Horiguchi K. Dynamic bending of cracked soft ferromagnetic plate in uniform magnetic field[J]. Theoretical and Applied France Mechanics, 1991, 15(3): 207–217. DOI:10.1016/0167-8442(91)90019-G |
| [8] |
付宇明, 郑丽娟, 任兴利.
含半埋藏共线双裂纹的Cr12合金钢试件电磁热止裂分析[J]. 兵工学报, 2008, 29(8): 944–949.
FU Yuming, ZHENG Lijuan, REN Xingli. Analysis of crack arrest in Cr12 alloy steel sample with half-embedding in-line crack using electromagnetic heating effect[J]. Acta Armamentarii, 2008, 29(8): 944–949. (in Chinese) |
| [9] |
付宇明, 白象忠, 许志强.
带有中间裂纹载流薄板放电瞬间耦合场的数值模拟[J]. 固体力学学报, 2002, 23(3): 306–311.
FU Yuming, BAI Xiangzhong, XU Zhiqiang. Numerical simulation of coupled field in a current-carrying plate with a central crack[J]. Acta Mechanica Solida Sinica, 2002, 23(3): 306–311. (in Chinese) |
| [10] |
付宇明, 郑丽娟, 刘禹.
含半埋藏空间裂纹的Cr12冷冲凹模电磁热止裂分析[J]. 中国机械工程, 2008, 19(10): 1224–1227.
FU Yuming, ZHENG Lijuan, LIU Yu. Analysis on the crack arrest in Cr12 cold punch cavity die with half-embedding spatial crack by using electromagnetic heating[J]. China Mechanical Engineering, 2008, 19(10): 1224–1227. DOI:10.3321/j.issn:1004-132X.2008.10.022 (in Chinese) |
| [11] |
刘俊杰, 白象忠, 郑坚, 等.
带有两个共线裂纹载流薄板的温度场及热应力强度因子[J]. 机械强度, 2007, 29(1): 103–108.
LIU Junjie, BAI Xiangzhong, ZHENG Jian, et al. Temperature field and thermal stress intensity factors of a current-carrying plate with two collinear cracks[J]. Journal of Mechanical Strength, 2007, 29(1): 103–108. (in Chinese) |
| [12] |
范华林, 陈平.
电磁热效应理论在薄板止裂技术上的应用[J]. 兵工学报, 2005, 26(6): 791–794.
FAN Hualin, CHEN Ping. Crack arrest effect in thin plates[J]. Acta Armamentarii, 2005, 26(6): 791–794. (in Chinese) |
| [13] | Zheng Lijuan, FU Yuming. Analysis on the temperature field when crack arresting in an axial symmetry metal die by pulse current discharged[J]. Key Engineering Materials, 2007(348/349): 765–768. |
| [14] | Fu Y M, Zhou H M, Wang J L, et al. Analysis of crack arrest by electromagnetic heating in metal with oblique-elliptical embedding crack[J]. Key Engineering Materials, 2012, 525/526: 405–408. DOI:10.4028/www.scientific.net/KEM.525-526 |
| [15] | Fu Y M, Bai X Z, Qiao G Y. Technique for producing crack arrest by electromagnetic heating[J]. Materials Science and Technology, 2001(17): 1653–1656. |
| [16] | 白象忠, 田振国, 郑坚. 断裂力学中的电热效应[M]. 北京: 国防工业出版社, 2009. |
| [17] |
郑丽娟, 周红梅, 付宇明.
含圆形埋藏裂纹金属构件的止裂应力强度因子[J]. 塑性工程学报, 2011, 18(5): 121–125.
ZHENG Lijuan, ZHOU Hongmei, FU Yuming. Analysis on stress intensity factor for crack arresting of metal structure with circular buried crack[J]. Journal of Plasticity Engineering, 2011, 18(5): 121–125. (in Chinese) |
| [18] | 侯镇冰, 何绍杰, 李恕先. 固体热传导[M]. 上海: 上海科学技术出版社, 1984. |
| [19] |
郑丽娟, 周红梅, 刘会莹, 等.
含埋藏空洞缺陷金属构件电磁热止裂强化分析[J]. 中国机械工程, 2012, 23(11): 1285–1288.
ZHENG Lijuan, ZHOU Hongmei, LIU Huiying, et al. Analysis on crack arresting and strengthening of metal structures with embedding hole defects by using electromagnetic heating[J]. China Mechanical Engineering, 2012, 23(11): 1285–1288. DOI:10.3969/j.issn.1004-132X.2012.11.006 (in Chinese) |
 2014, Vol. 37
2014, Vol. 37

