2. 陆军航空兵学院, 北京 101123
2. Army Aviation Institute, Beijing 101123, China
斯特林发动机是一种闭循环回热式发动机,是除蒸汽机和内燃机之外的又一类往复式动力机械[1]。它的内部流动是可压缩工质的非定常交变流动,因此对其进行模拟计算是困难的。Finkelstein[2]提出了斯特林发动机的绝热分析法。Li等[3]对一个太阳能斯特林发动机进行了二级分析,采用Euler数值计算方法离散求解常微分方程。Parlak等[4]对自由活塞式斯特林发动机进行了绝热分析,并与Schmidt等温分析进行了比较,解决了自由活塞式斯特林发动机特有的非线性偏微分方程求解问题。到目前为止,国内外很少有针对热力学分析法的计算误差及其缺点的研究。
基于机械损失的估算,加热器和冷却器的温度校核,提出了斯特林发动机热力循环的热力分析模型[5],运用GPU-3斯特林发动机的试验数据对该热力分析方法进行了验证;为斯特林发动机热力循环分析提出了一种有效的热力分析方法。
1 系统组成水下斯特林发动机系统主要由热管反应器、斯特林发动机两部分组成。
1.1 热源传统的斯特林发动机能够利用太阳能、生物质能及地热能等一系列外部能源,但是,对于水下环境,无法从中获取足够的能源,需要为其系统提供足够的能源。
Li/SF6反应系统具有比能量高等特点,是应用于水下航行器热源的首选,Li/SF6反应主要分为两种形式:浸没燃烧、热管燃烧。浸没燃烧方式主要工作在大功率、短时间的应用场合。而热管燃烧热管反应器适用于小功率、长时间的应用场合。因此,对于设计小功率输出条件的水下斯特林发动机系统,热源选用Li/SF6热管燃烧方式。
1.2 斯特林发动机水下的工作环境以及尺寸限制决定了斯特林发动机应设计为紧凑型,目前最有前途的布置方式为双作用发动机,是指气缸中的活塞既起压缩活塞的作用又起膨胀活塞的作用。这样,4个气缸和4个活塞以及4套热交换器,组成4个完整的闭式循环系统,相当于
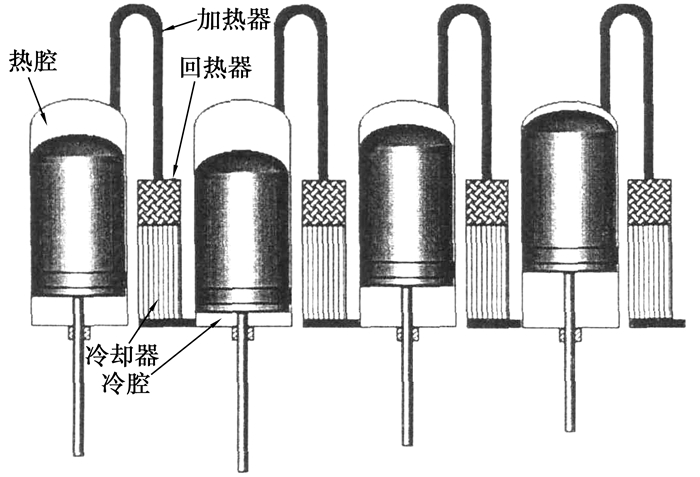
综上所述,对于水下的斯特林发动机系统,可以选择以Li/SF6热管燃烧方式作为其热源,发动机布置为4缸双作用形式[6]。其结构简图如图 1所示。
|
图 1 水下斯特林发动机系统结构简图 |
为了分析水下斯特林发动机系统,根据Urieli的绝热分析方法,进行了机械损失以及温度校核等方面的修正,用于水下斯特林发动机的分析。因为热管燃烧方式目前还没有具体的研究,这里并不分析。
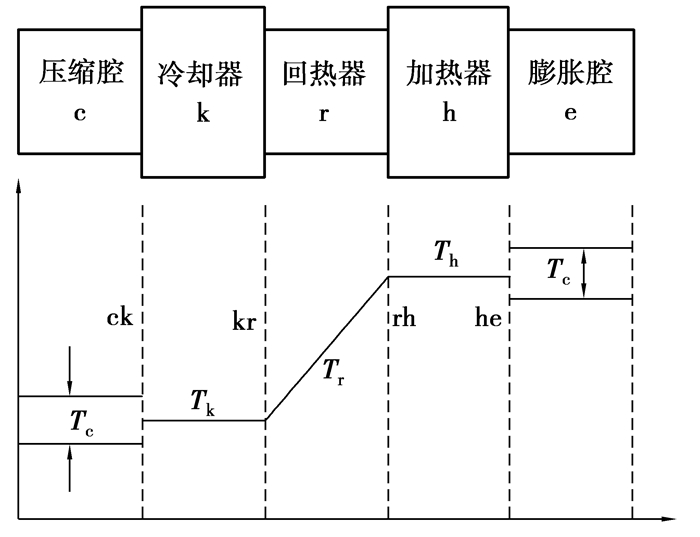
斯特林发动机的闭式循环系统由压缩腔、冷却器、回热器、加热器和膨胀腔组成[7],如图 2所示。斯特林发动机建模分析过程的主要简化假设有[8]:
|
图 2 斯特林发动机温度示意图 |
1) 发动机运行时工作腔与外界绝热;
2) 系统各处的瞬时压力相等;
3) 工质遵循理想气体状态方程,且一维稳定流动;
4) 缸壁、活塞及死容积中工质的温度恒定。
在理想绝热分析法中,压缩腔和膨胀腔内的工质温度Tc、Te在循环过程中是不断变化的。而冷却器和加热器内工质的温度Tk、Th是恒定的,回热器内的温度则沿轴向线性变化,平均温度Tr取Tk和Th的对数平均值(下标c、k、r、h、e分别代表压缩腔、冷却器、回热器、加热器和膨胀腔;ck、kr、rh、he分别代表各区域的边界)。
压缩腔和膨胀腔的瞬时容积Vc、Vh为
| $ {V_{\rm{c}}} = \frac{1}{2}{V_{{\rm{sc}}}}\left[ {1 + \cos \left( {\alpha - \varphi } \right)} \right] + {V_{{\rm{cc}}}}, $ | (1) |
| $ {V_{\rm{h}}} = \frac{1}{2}{V_{{\rm{se}}}}\left( {1 + \cos \;\alpha } \right) + {V_{{\rm{ce}}}}, $ | (2) |
式中:Vsc、Vse分别为压缩腔和膨胀腔的扫气容积;Vcc、Vce分别为压缩腔和膨胀腔的余隙容积;
斯特林发动机的工质总质量M可由等温分析法计算[9]。斯特林发动机的二阶分析模型方程组如下[10]。
压力p及压力变化dp为
| $ p = \frac{{MR}}{{{V_{\rm{c}}}/{T_{\rm{c}}} + {V_{\rm{k}}}/{T_{\rm{k}}} + {V_{\rm{r}}}/{T_{\rm{r}}} + {V_{\rm{h}}}/{T_{\rm{h}}} + {V_{\rm{e}}}/{T_{\rm{e}}}}}, $ | (3) |
| $ {\rm{d}}p = \frac{{ - \gamma p\left( {\frac{{{\rm{d}}{V_{\rm{c}}}}}{{{T_{{\rm{ck}}}}}} + \frac{{{\rm{d}}{V_{\rm{e}}}}}{{{T_{{\rm{he}}}}}}} \right)}}{{\frac{{{V_{\rm{c}}}}}{{{T_{{\rm{ck}}}}}} + \gamma \left( {\frac{{{V_{\rm{k}}}}}{{{T_{\rm{k}}}}} + \frac{{{V_{\rm{r}}}}}{{{T_{\rm{r}}}}} + \frac{{{V_{\rm{h}}}}}{{{T_{\rm{h}}}}}} \right) + \frac{{{V_{\rm{e}}}}}{{{T_{{\rm{he}}}}}}}}。$ | (4) |
控制区的质量为
| $ \left. \begin{array}{l} {m_{\rm{c}}} = \frac{{p{V_{\rm{c}}}}}{{R{T_{\rm{c}}}}},{m_{\rm{k}}} = \frac{{p{V_{\rm{k}}}}}{{R{T_{\rm{k}}}}},{m_{\rm{r}}} = \frac{{p{V_{\rm{r}}}}}{{R{T_{\rm{r}}}}},\\ {m_{\rm{e}}} = \frac{{p{V_{\rm{e}}}}}{{R{T_{\rm{e}}}}},{m_{\rm{h}}} = \frac{{p{V_{\rm{h}}}}}{{R{T_{\rm{h}}}}}。\end{array} \right\} $ | (5) |
控制区的质量变化量为
| $ \left. \begin{array}{l} {\rm{d}}{m_{\rm{c}}} = \frac{{p{\rm{d}}{V_{\rm{c}}} + {V_{\rm{c}}}\frac{{{\rm{d}}p}}{\gamma }}}{{R{T_{{\rm{ck}}}}}},\\ {\rm{d}}{m_{\rm{e}}} = \frac{{p{\rm{d}}{V_{\rm{e}}} + {V_{\rm{e}}}\frac{{{\rm{d}}p}}{\gamma }}}{{R{T_{{\rm{he}}}}}},\\ {\rm{d}}{m_{\rm{e}}} = \frac{{p{\rm{d}}{V_{\rm{e}}} + {V_{\rm{e}}}\frac{{{\rm{d}}p}}{\gamma }}}{{R{T_{{\rm{he}}}}}},\\ d{m_{\rm{k}}} = \frac{{{m_{\rm{k}}}{\rm{d}}p}}{p},d{m_{\rm{r}}} = \frac{{{m_{\rm{r}}}{\rm{d}}p}}{p},d{m_{\rm{h}}} = \frac{{{m_{\rm{h}}}{\rm{d}}p}}{p}。\end{array} \right\} $ | (6) |
边界质量流量为
| $ \left. \begin{array}{l} {{\dot m}_{{\rm{ck}}}} = - {\rm{d}}{m_{\rm{c}}},{{\dot m}_{{\rm{kr}}}} = {{\dot m}_{{\rm{ck}}}} - {\rm{d}}{m_{\rm{c}}},\\ {{\dot m}_{{\rm{he}}}} = {\rm{d}}{m_{\rm{e}}},{{\dot m}_{{\rm{rh}}}} = {{\dot m}_{{\rm{he}}}} - {\rm{d}}{m_{\rm{h}}}。\end{array} \right\} $ | (7) |
边界温度为
| $ \left. \begin{array}{l} {\;\;\;\;\;\;\;\;\;\;\;\;\;T_{{\rm{kr}}}} = {T_{k}},{T_{{\rm{rh}}}} = {T_{\rm{h}}},\\ 如果{{\dot m}_{{\rm{ck}}}} > 0,则{T_{{\rm{ck}}}} = {T_{\rm{c}}},否则{T_{{\rm{ck}}}} = {T_{k}},\\ 如果{{\dot m}_{{\rm{he}}}} > 0,则{T_{{\rm{he}}}} = {T_{\rm{h}}},否则{T_{{\rm{he}}}} = {T_{\rm{e}}}, \end{array} \right\} $ | (8) |
压缩腔和膨胀腔的温度变化为
| $ \left. \begin{array}{l} {\rm{d}}{T_\rm{c}} = {T_\rm{c}}\left( {\frac{{{\rm{d}}p}}{p} + \frac{{{\rm{d}}{V_{\rm{c}}}}}{{{V_{\rm{c}}}}} - \frac{{{\rm{d}}{m_{\rm{c}}}}}{{{m_{\rm{c}}}}}} \right),\\ {\rm{d}}{T_{\rm{e}}} = {T_{\rm{e}}}\left( {\frac{{{\rm{d}}p}}{p} + \frac{{{\rm{d}}{V_{\rm{e}}}}}{{{V_{\rm{e}}}}} - \frac{{{\rm{d}}{m_{\rm{e}}}}}{{{m_{\rm{e}}}}}} \right)。\end{array} \right\} $ | (9) |
功及换热
| $ \left. \begin{array}{l} d{Q_{\rm{k}}} = \frac{{{V_{\rm{k}}}{\rm{d}}p{c_V}}}{R} - {c_p}\left( {{T_{{\rm{ck}}}}{{\dot m}_{{\rm{ck}}}} - {T_{{\rm{kr}}}}{{\dot m}_{{\rm{kr}}}}} \right),\\ d{Q_{\rm{r}}} = \frac{{{V_{\rm{r}}}{\rm{d}}p{c_V}}}{R} - {c_p}\left( {{T_{{\rm{kr}}}}{{\dot m}_{{\rm{kr}}}} - {T_{{\rm{rh}}}}{{\dot m}_{{\rm{rh}}}}} \right),\\ d{Q_{\rm{h}}} = \frac{{{V_{\rm{h}}}{\rm{d}}p{c_V}}}{R} - {c_p}\left( {{T_{{\rm{rh}}}}{{\dot m}_{{\rm{rh}}}} - {T_{{\rm{he}}}}{{\dot m}_{{\rm{he}}}}} \right),\\ {\rm{d}}{W_{\rm{c}}} = p{\rm{d}}{V_{\rm{c}}},{\rm{d}}{W_{\rm{e}}} = p{\rm{d}}{V_{\rm{e}}},\\ {\rm{d}}W = {\rm{d}}{W_{\rm{c}}}{\rm{ + d}}{W_{\rm{e}}},W = {W_{\rm{c}}} + {W_{\rm{e}}}, \end{array} \right\} $ | (10) |
式中:m、T、p、V分别代表工质质量、温度、压力、体积。
3 发动机热损失和机械损失的估算 3.1 回热器的热损失假设回热器有效度为ε,则循环回热损失为
| $ {Q_{{\rm{r1}}}} = {Q_{\rm{r}}}\left( {1 - \varepsilon } \right), $ | (11) |
式中Qr为理想回热器的循环回热量。
一个循环内回热器外壳轴向热损失为
| $ {Q_{{\rm{wr}}}} = \frac{{{k_{{\rm{wr}}}}{A_{{\rm{wr}}}}\left( {{T_{\rm{h}}} - {T_{\rm{k}}}} \right)}}{{{l_{\rm{r}}}n}}, $ | (12) |
式中:kwr为回热器外壳的导热系数,Awr为回热器外壳横截面面积;lr为回热器长度;n为机轴转速。
3.2 压力损失压力损失主要是由加热器、回热器和冷却器引起,因此这里只考虑换热器内的压力损失。假设换热器内工质流动为准稳态流动,则有
| $ F + \Delta pA = 0, $ | (13) |
式中:F为流动摩擦阻力;Δp为工质的压力损失;A为自由流动横截面面积。
3.3 机械损失United Stirling公司根据斯特林发动机的试验结果,拟合得到机械损失的计算公式[11]
| $ M = 12.8\frac{n}{{{n_{\rm{d}}}}}\frac{{{p_{\rm{m}}} + 5}}{{20}}, $ | (14) |
式中:M为机械损失,kW;n为发动机转速,r/min;nd为发动机的设计转速,r/min;pm为平均工作压力,MPa,该公式同时也包括了由于泄漏造成的损失。
3.4 输入及输出功率在二级简化模型中,为简化压力计算,将理想绝热分析所得的工质循环压力作为压缩腔内工质压力,则循环做功量为
| $ \begin{array}{l} W = {W_{\rm{c}}} + {W_{\rm{e}}} = \int {p{\rm{d}}{V_{\rm{c}}}} + \int {\left( {p - \sum {\Delta p} } \right){\rm{d}}{V_{\rm{e}}}} \\ = \int {p\left( {{\rm{d}}{V_{\rm{c}}} + {\rm{d}}{V_{\rm{e}}}} \right) - \int {\sum {\Delta p{\rm{d}}{V_{\rm{e}}}} } } , \end{array} $ | (15) |
式中
斯特林发动机输出功率为
| $ {W_{\rm{o}}} = W - {\rm{ML}}。$ | (16) |
斯特林发动机输入功率为
| $ {Q_{\rm{i}}}{\rm{ = }}{Q_{\rm{h}}}{\rm{ + }}{Q_{{\rm{r1}}}}{\rm{ + }}{Q_{{\rm{wr}}}}。$ | (17) |
冷却器的壳程流动属于流体横掠管束,管束为叉排排列方式。根据Zhukauskas公式[12],可得流体横掠叉排管束平均表面传热系数Nuko。因此,冷却器壳程的换热系数为
| $ {h_{_{{\rm{ko}}}}} = N{u_{{\rm{ko}}}}\frac{{{\lambda _{{\rm{ko}}}}}}{{{D_{\rm{k}}}}}, $ | (18) |
式中:Dk为冷却器的内径; λko为冷却水的导热系数。
冷却器的内管与外管之间的导热,单个管路热阻为
| $ {R_{\rm{kw}}} = \frac{{\ln \frac{{{R_{{\rm{ko}}}}}}{{{R_{{\rm{ki}}}}}}}}{{2{\rm{ π }}{\lambda _{\rm{w}}}{l_{\rm{k}}}}}, $ | (19) |
式中:Rko、Rki分别为冷却器管的外径和内径;lk为冷却器管长;λw为冷却器管的导热系数。
综上,冷却器管外流体与管内工质的温差为
| $ \Delta {T_\rm{k}} = {Q_\rm{k}}\left( {\frac{1}{{{R_{{\rm{kw}}}}{N_{{\rm{tk}}}}}} + \frac{1}{{{h_{{\rm{ki}}}}{A_{{\rm{ki}}}}}} + \frac{1}{{{h_{{\rm{ko}}}}{A_{{\rm{ko}}}}}}} \right), $ | (20) |
式中:Ntk为冷却器的管数;Ako和Aki分别为冷却器管外、内表面积;hki为冷却器管槽内部的对流换热系数。
4.2 加热器温度校核加热管内的对流换热系数hhi可由文献[13]计算得到。加热器管内外壁的导热热阻为
| $ {R_{{\rm{h}}w}} = \frac{{\ln \frac{{{R_{{\rm{ho}}}}}}{{{R_{{\rm{hi}}}}}}}}{{2{\rm{ \mathit{ π} }}{\lambda _{\rm{h}}}{l_{\rm{h}}}}}, $ | (21) |
式中:Rho和Rhi分别为加热器管的外径和内径;λh为加热器管的导热系数;lh为加热器管长度。
综上,加热器管外壁与管内工质的温差为
| $ \Delta {T_{\rm{h}}} = {Q_{\rm{h}}}\left( {\frac{1}{{{R_{{\rm{hw}}}}{N_{{\rm{th}}}}}} + \frac{1}{{{h_{{\rm{hi}}}}{A_{{\rm{hi}}}}}}} \right), $ | (22) |
式中:Nth为加热器的管数; Ahi为加热器管的内表面积。
因此,加热器管内工质的温度和冷却器管内壁的温度T′h、T′k为
| $ {{T'}_{\rm{h}}} = {T_{{\rm{hw}}}} - \Delta {T_{\rm{h}}}, $ | (23) |
| $ {{T'}_{\rm{k}}} = {T_{{\rm{kw}}}} + \Delta {T_{\rm{k}}}, $ | (24) |
式中:Tkw为冷却水的进口温度;Thw为加热器管外壁的温度。
5 模型验证GPU-3斯特林发动机是美国通用汽车公司为陆军研制的便携式发电机组,GPU-3斯特林发动机的具体参数如表 1所示[14]。NASA Lewis Research Center测试了该发动机在不同转速、平均工作压强条件下的输入与输出功率。
| 表 1 GPU-3型斯特林发动机参数表 |
这里运用提出的热力循环模型,分析在试验条件下发动机的输入及输出功率,验证理论的热力模型误差,具体结果如图 3、4所示。
|
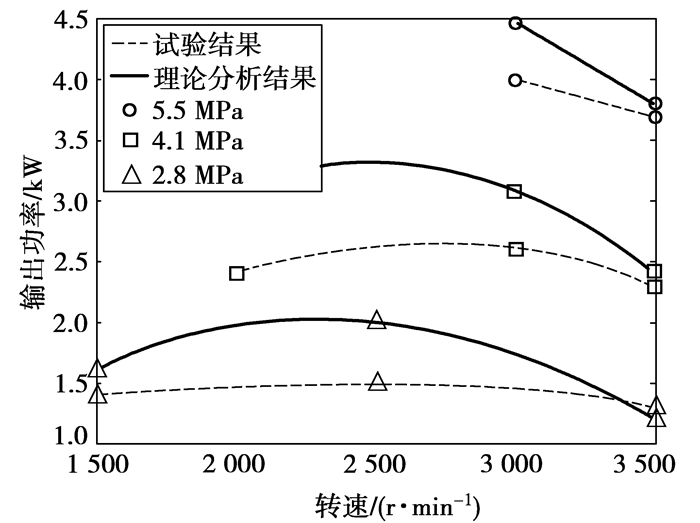
图 3 理论与试验分析输出功率对比图 |
|
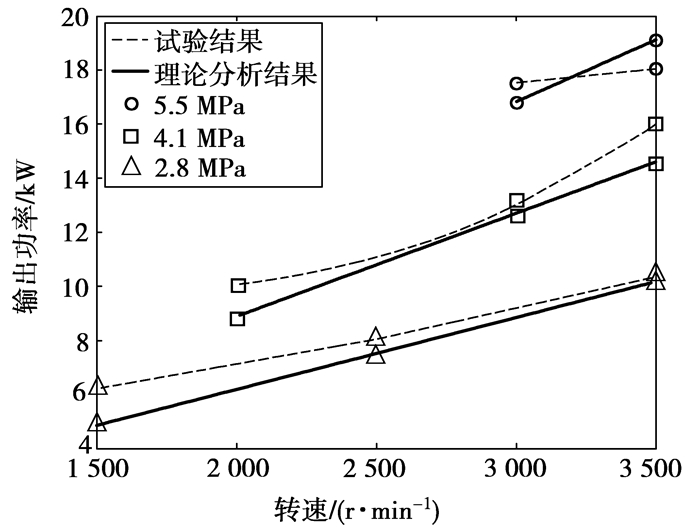
图 4 理论与试验分析输入功率对比图 |
所有理论分析与试验工作条件均为加热器管外壁温度为963 K,冷却水进口温度为293 K,发动机的工质为氦气,图 3给出了理论热力学模型分析结果与试验结果的输出功率对比,图 4给出了理论热力学模型模型分析结果与试验结果的输入功率对比。由图 3和图 4可得出,理论模型结果相对于试验分析结果的输出功率最大误差不超过19 %,输入功率理论模型结果的最大误差不超过16 %。
文献[15]用二阶分析模型模拟GPU-3发动机的输入及输出功率,两种方法的误差对比如表 2、3所示,可见运用提出的热力学模型的输出功率及输入功率的误差较传统二阶分析模型误差有显著的减小,能更精确地描述斯特林发动机的工作特性。
| 表 2 不同平均压力GPU-3发动机输出功率计算误差值 |
| 表 3 不同平均压力GPU-3发动机输入功率计算误差值 |
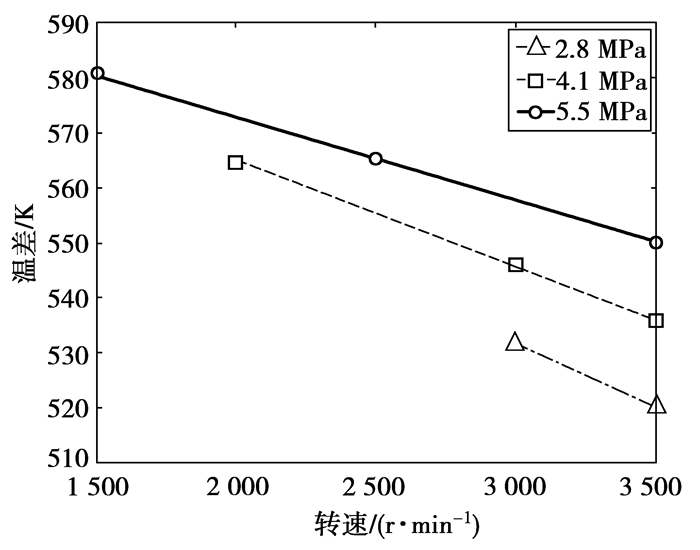
当加热器管外壁及冷却水的温度固定时,随着发动机转速升高,输入功率增大,从而加热器内外的温度梯度增大,管内温度减小;同理可得,随着转速的增大,冷却器管内的温度升高。膨胀腔和压缩腔的温度差如图 5所示,综上,对应不同的平均工作压强,斯特林发动机有最佳的工作转速。
|
图 5 试验工况时膨胀腔和压缩腔的温度差 |
1) 对比NASA的试验数据,提出的热力学分析模型模拟的输出功率的最大误差不超过19%,而输入功率与试验数的最大误差不超过16%。
2) 相对于传统的二阶热力分析模型,此种热力学循环模型的模拟输出和输入功率的误差更小,能更好地分析发动机的工作特性;
3) 当加热器外壁与冷却水进口温度固定时,对于特定尺寸的斯特林发动机,存在最佳工作转速,使输出功率最大。
| [1] | Campos M C, Vargas V C, Ordonez J C. Thermodynamic optimization of a Stirling engine[J]. Energy, 2012, 44(1): 902–910. DOI:10.1016/j.energy.2012.04.060 |
| [2] | Finkelstein T. Generalized thermodynamic analysis of Stirling engine[M]. Detroit: Society of Automotive Enginineers, 1960. |
| [3] | Li Y Q, He Y L, Wang W W. Optimization of solar-powered Striling heat engine with finite time thermodynamicst[J]. Renewable Energy, 2011, 36(1): 421–427. DOI:10.1016/j.renene.2010.06.037 |
| [4] | Parlak N, Wagner A, Elsner M, et al. Thermodynamic analysis of a gamma type Stirling engine in non-ideal adiabatic conditions[J]. Renewable Energy, 2009, 34(1): 266–273. DOI:10.1016/j.renene.2008.02.030 |
| [5] | Martini W R. Stirling engine design manual[M]. London: The Office, 1978. |
| [6] | Karabulut H, Yücesu H S, Cinar C. Nodal analysis of a Stirling engine with concentric piston and displacer[J]. Renewable Energy, 2006, 31(13): 2188–2197. DOI:10.1016/j.renene.2005.12.009 |
| [7] | Abdullah S, Yousif B F, Sopian K. Design consideration of low temperature differential double-acting Stirling engine for solar application[J]. Renewable Energy, 2005, 30(12): 1923–1941. DOI:10.1016/j.renene.2004.11.011 |
| [8] | Thombare D G, Verma S K. Technological development in the Stirling cycle engines[J]. Renewable and Sustainable Energy Reviews, 2008, 12(1): 1–38. DOI:10.1016/j.rser.2006.07.001 |
| [9] | Walker G. Stirling engine[M]. UK: Oxford University Press, 1980. |
| [10] | Urieli I, Berchowitz D M. Stirling cycle engine analysis[M]. Bristol: Adam Hilger, 1984. |
| [11] | Tew R C, Jr. Computer program for Stirling engine performance calculation[R].Washington:National Aeronautics and Space Administration Lewis Research Center, 1983. |
| [12] | Abdullah S, Yousif B F, Sopian K. Design consideration of low temperature differential double-acting Stirling engine for solar application[J]. Renewable Energy, 2005, 30(12): 1923–1941. DOI:10.1016/j.renene.2004.11.011 |
| [13] | Kuosa M, Saari K, Kankkunen A, et al. Oscillating flow in a Stirling engine heat exchanger[J]. Applied Thermal Engineering, 2012, 45/46: 15–23. DOI:10.1016/j.applthermaleng.2012.03.023 |
| [14] | Timoumi Y, Tlili I, Nasrallah S B. Design and performance optimization of GPU-3 Stirling engines[J]. Energy, 2008, 33(7): 1100–1114. DOI:10.1016/j.energy.2008.02.005 |
| [15] |
胡学光, 董金钟, 王明昆.
斯特林发动机绝热分析法研究[J]. 应用能源技术, 2009(8): 41–45.
HU Xueguang, DONG Jinzhong, WANG Mingkun. Study on the adiabatic analysis of Stirling engine[J]. Applied Energy Technology, 2009(8): 41–45. (in Chinese) |
 2014, Vol. 37
2014, Vol. 37


